Math proc templates for Prime Number generation and TCL demo example, numerical analysis
Math proc templates for Prime Number generation and TCL demo example, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks,gold 30Apr2021
- Math proc templates for Prime Number generation and TCL demo example, numerical analysis
- Introduction
- prime number formula < 16n+15 >
- Prime Numbers on Clay Tablets
- Applications for proc ::math::quantity_into_ratios
- Quadratic Equation Solution from Muller's method
- Conclusions
- Subroutine Template 1, quantity_into_multiple_ratios
- Printout for quantity_into_ratios proc
- Subroutine Template 2, sqrt_sum_of_squares
- output for sqrt_sum_of_squares
- Pseudocode, Equations, and Wiki Page Checklist
- Subroutine Template 3, geometric_mean
- Subroutine Template 4, list of normalized_set
- Test Suite printout for list of normalized_set
- Possible Errors, Predefined Entries, Break Lines, Possible Wild_Cards in TCLLIB::math local copy
- Testcases Section
- Screenshots Section
- Screenshots Section
- figure 1a. Console wrapper for prime_formula proc
- figure 1b, Console wrapper for sqrt_sum_of_squares
- figure 1c, Console wrapper for sqrt_sum_of_squares
- figure 1d, Console wrapper for normalized_set
- figure 1e, Market_Rate_Problem
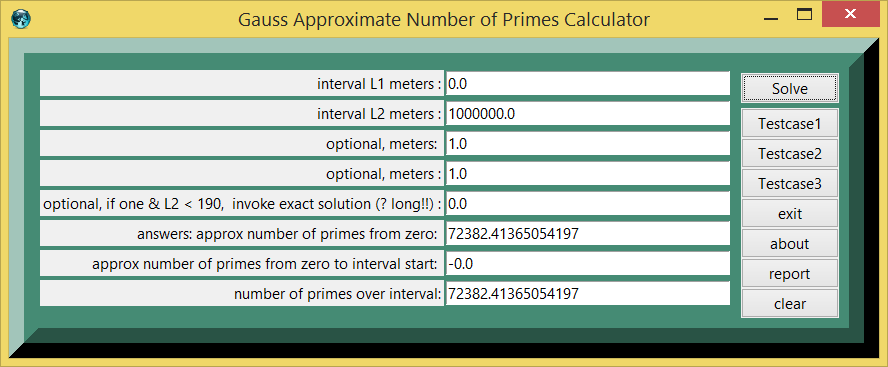
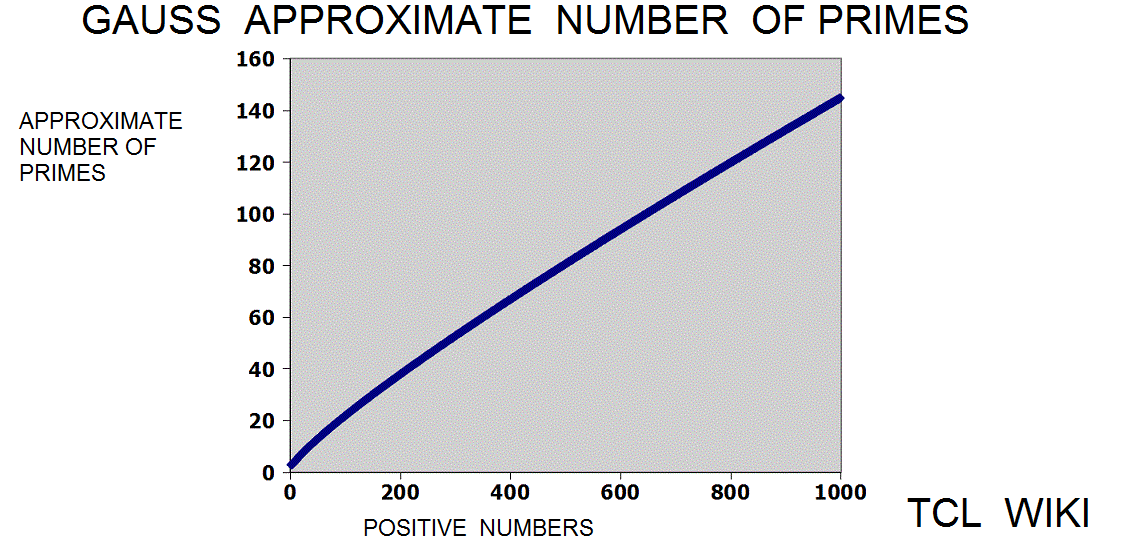
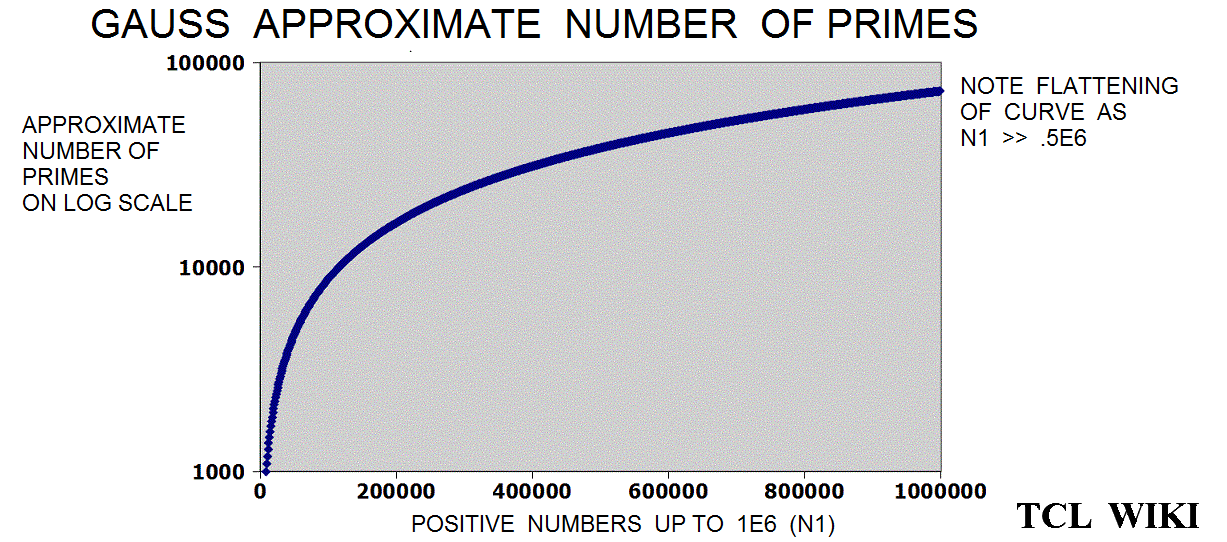
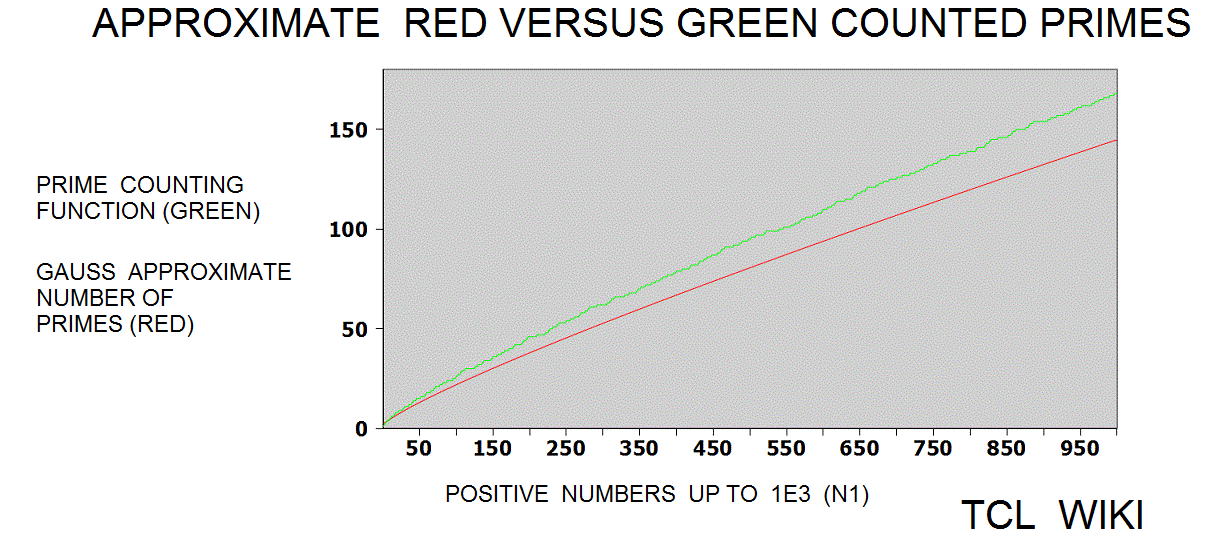
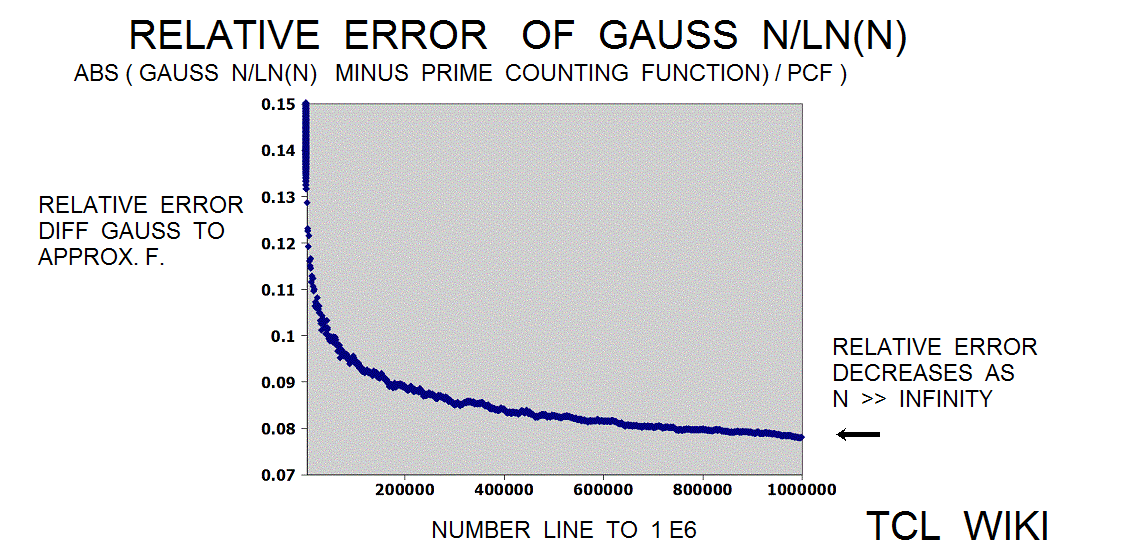
- figure 1e, Gauss Approximate Number of Primes
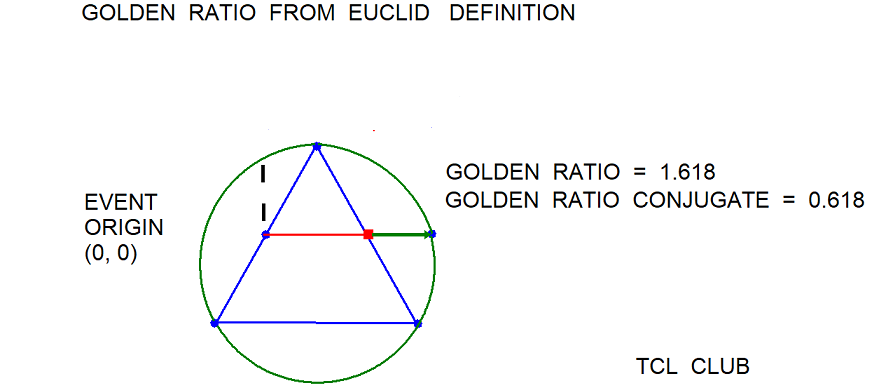
- figure 1f, Golden_Ratio_definition
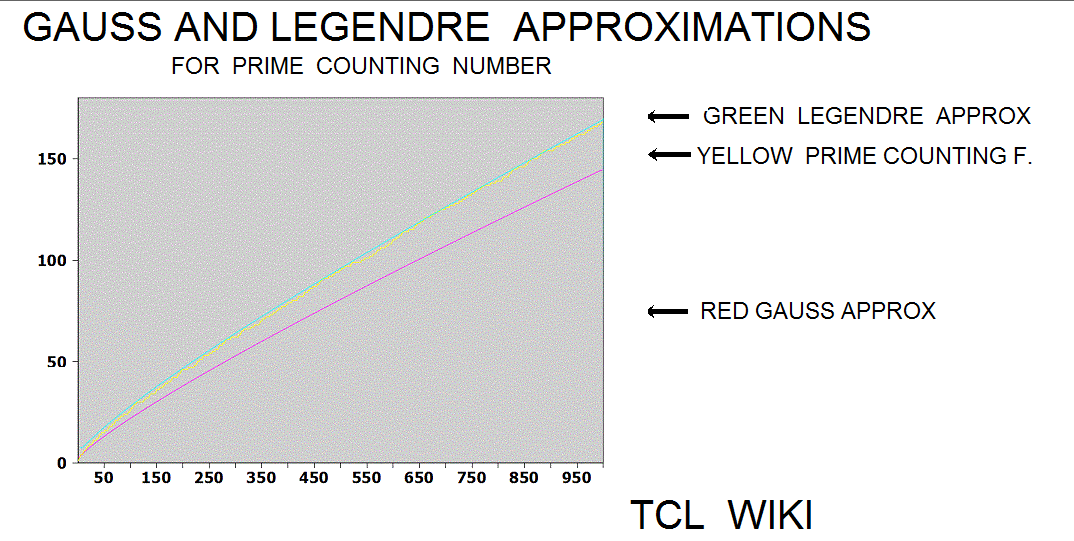
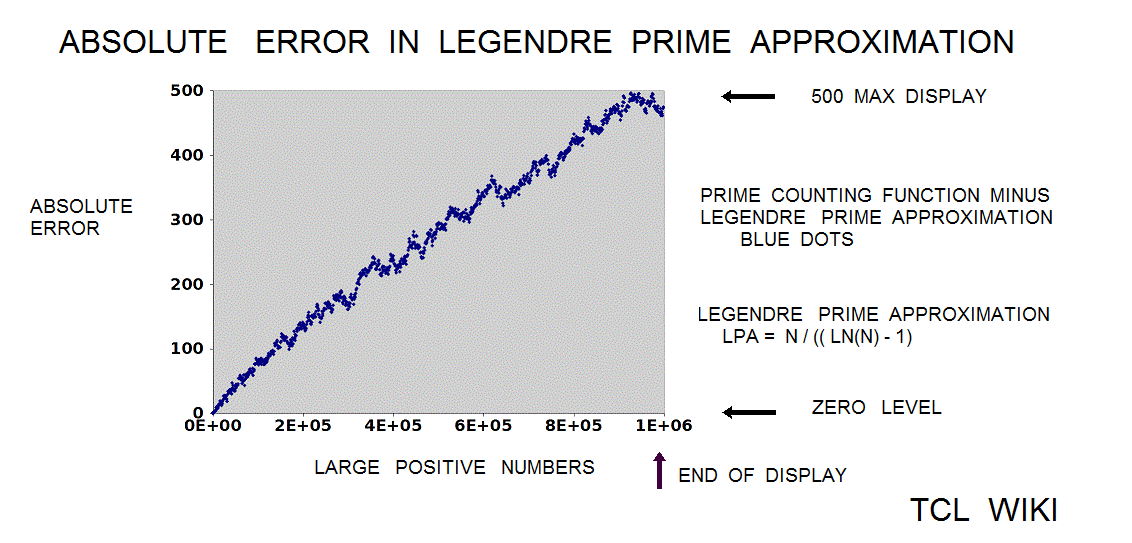
- figure 2.
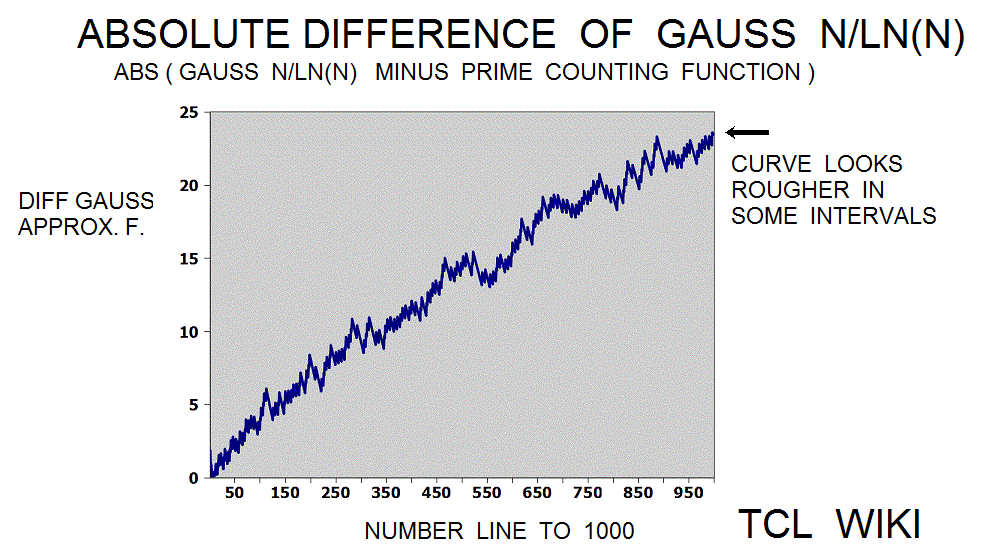
- figure 3.
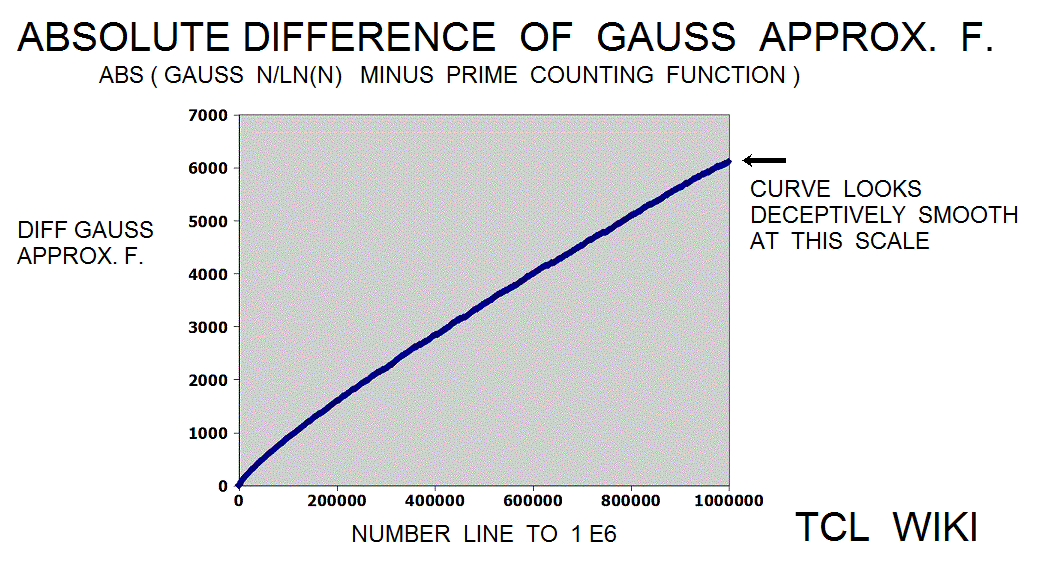
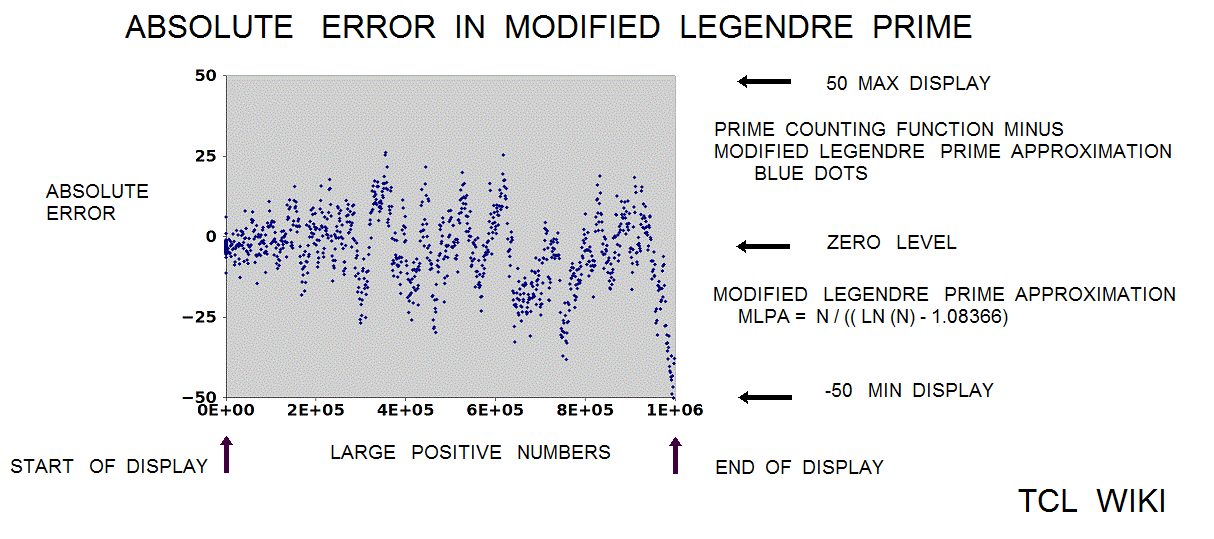
- figure 4.
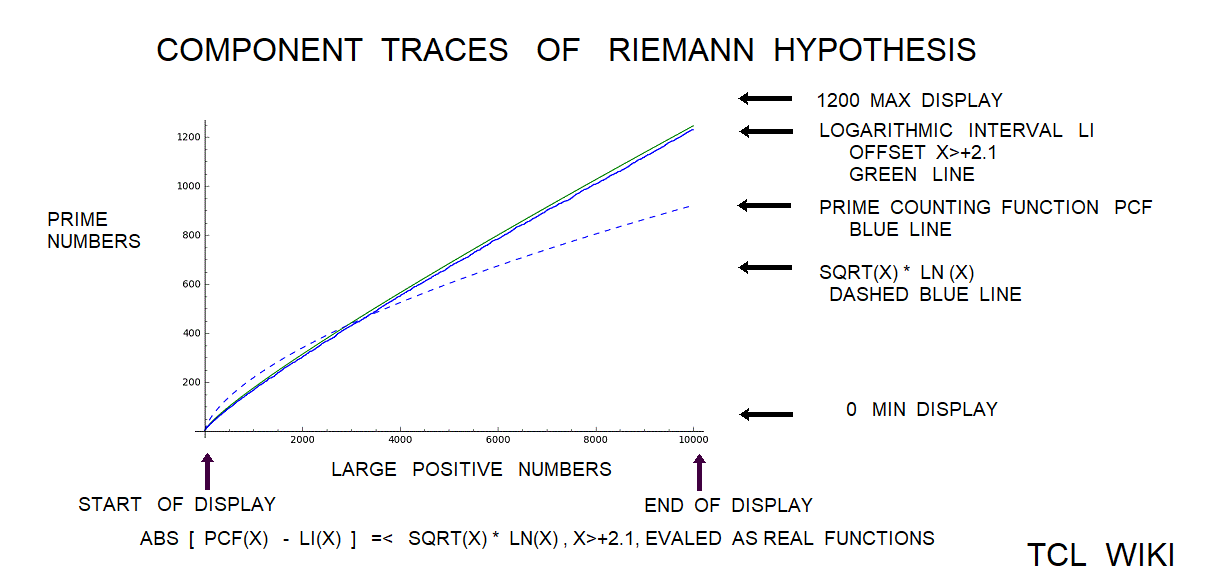
- figure 5.
- figure 6.
- figure 7.
- figure 8.
- figure 9.
- figure 10.
- figure 11.
- figure 12.
- References:
- References:
- Updating Plimpton 322, Babylonian tablet References:
- References on Quadratic Equations:
- Appendix Code
- appendix TCL programs and scripts
- Subroutine Template 4, prime_formula
- Subroutine Template 5, Combined Market Rate formula
- Subroutine Template 6, Quadratic Equation Solution, Muller's method
- Printout for Subroutine Template 6, Quadratic Equation Solution, Muller's method
- Gamblers_Ruin_Expectation
- Gamblers Ruin Expectation E(P(N)) Application to Random Walks
- Hidden Comments Section
Introduction
gold Here are some Math proc templates for Prime Number generation. These Math proc templates are intended to be compatible with the format of existing subroutines in the TCLLIB:math library. The new Math proc should be checked in TCLLIB::math local copy on your personal computer before submission to TCLLIB ticket pipeline. Morfing these math proc templates into Prime Number generation subroutines should be feasible. I have found it easier and more tidy to start with a working TCL math template and morf a few lines into a new purpose.If one completes and tests the new TCL subroutine in a console program, then usually one can load the new TCL subroutine into a graphical user interface (gui).
gold Update 3/2/2024. This page on developing pseudocode examples and one line procedures is not a replacement for the current Tcl core and Tcllib, which is much improved since Tcl version 4, and other <faster> language constructs. math ops, Tcllib routines, and other compiled routines can reduce the cost of big-data tasks by about 1/3. The time savings of the core and Tcllib are not always obvious on small quantities of data, like 4 or 5 numbers. Performance of one-line programs may suffer degradation due to lengthy recursion calls, and may be limited by constraints on recursion. Dependence on math operator notation, helper procedures, math check examples, degradation due to lengthy recursion calls, and special library functions should be noted in the comment lines.
prime number formula < 16n+15 >
Maybe coincidence, but sequence {7 11 13 14 } has been found on Sumerian Tablet AO8862. The On-Line Encyclopedia of Integer Sequences A014311 Oeis {7 11 13 14} cited sequence property as Numbers n such that <16n+15> are prime. Tablet YBC10722 uses the input quantity 15 with the sequence {7 11 13 14}! KWJ in Monster Prime Predicting Formula has posted on the Wiki for this formula < 16n+15 >.
This prime number formula < 16n+15 > as a prime number filtering mechanism produces some primes and some duds. KWJ reported the prime number formula < 16n+15 > had an efficiency of 0.166 for filtering primes out of the numberline,for the data set, <PLT500K>. For N > 2, about half of numbers on the numberline are even, which could never be defined as primes. If the formula added two even numbers, then only even numbers would result in the sum with no primes produced. If the formula added an even number and odd number, then some odd numbers might result with some primes produced.
Prime Numbers on Clay Tablets
In some sense, the Plimpton 322 clay tablet is also generating a set of prime numbers in the available triplet collection on the clay tablet. The Babylonian regular numbers in base_60 between 0 and 60 have a limited set of triplets that satisfy 1< X-1/X < 1+sqrt(2) which appears to be the role of Plimpton 322. The limit 1< X-1/X < 1+sqrt(2) may explain the 1<X<2 limit on the Late Babylonian many place reciprocal tablets.
From the Plimpton 322 tablet, Fernando Quinonez reported that the prime numbers of the set d (column d) are coincedent with Gauss formula < 4n + 1> and that prime numbers of set a (column a) are mixed forms, including the Gauss formula <4n + 1> and another formula < 4n + 3>. On the Plimpton 322 tablet, 8 of 15 readable numbers were prime numbers. The percentage of prime numbers was expr { (8./15.) * 100.}, 53.3 percent rounded.
While the modern mathematicians are trying to find prime numbers in base_10, the Babylonian mathematicians in base_60 were trying to avoid prime numbers. The primes are the Achilles heel of the Babylonian multiplication system using reciprocals in base_60. The number set in the sequence {7 11 13 14} was especially foul to the Babylonian multiplication system, although the Babylonian mathematicians did use the set {7 11 13 14} in arithmetic or "advanced non-standard" calculations. One trick that the Babylonian mathematicians was to multiply an odd number or prime number by 2 or 3 at one early stage of the calculations and then divide out respectfully the 2 or 3 at a later stage of the calculations. For example, 7*2 converts an overtly prime number to a number 14 with factors 2*7. However, this multiplication trick with 2 or 3 as factors is confusing in the extant school and library tablets, so sometimes the modern reader is stressed by a missing factor of 2/3 after corrupted or dropped tablet lines.
Alternate text. For example, 7*2 converts an overtly prime number to a number 14 with factors 2*7. Now, the prime number 7 is overtly hidden as a factor of even number 14, a thorn among the roses. For another example, 3*8 converts an overtly prime number to a number 24 with factors 3*2*2*2. The set of Babylonian math operations had special terms for doubling and tripling numbers. Now, the prime number 3 is overtly hidden by successive doubling as a factor of even number 24. Continuing with the example of 3*8, the original number of 3 may be restored by successive division by factor of 2. There are student tablets or lists of doubling exercises in the Babylonian clay tablets. Successive doubling or tripling may be considered a Babylonian algorithm, as successive doubling was used in the Babylonian interest rate algorithm. See [L1 ]
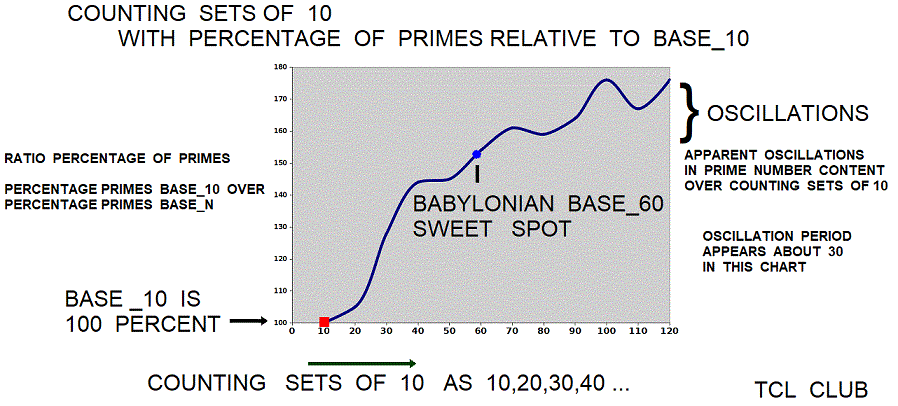
| table 1 Percentage Primes in Modern Base_10 and Babylonian Base_60 | printed in | tcl wiki format | |
|---|---|---|---|
| quantity | value | value | comment, if any |
| set_number: | percent of prime numbers in set | percent primes in set of 10 over / set of N | |
| set 10 : | 44.44 | 1.0 | Modern base_10 |
| set 20 : | 42.10 | 1.05 | Archaic IndoEuropean base_20 |
| set 30 : | 34.48 | 1.28 | |
| set 40 : | 30.76 | 1.44 | |
| set 50 : | 30.61 | 1.45 | |
| set 60 : | 28.81 | 1.54 | Babylonian base_60 |
| set 70 : | 27.53 | 1.61 | |
| set 80 : | 27.84 | 1.59 | |
| set 90 : | 26.96 | 1.64 | |
| set 100 : | 25.25 | 1.76 | |
| set 110 : | 26.60 | 1.67 | |
| set 120 : | 25.21 | 1.76 |
;# using TCLLIB math prime subroutines
;# COUNTING SETS OF 10 WITH PERCENTAGE OF PRIMES RELATIVE TO BASE_10
puts "%| set_number:|percent of prime numbers in set | |%"
foreach value {10 20 30 40 50 60 70 80 90 100 110 120} {
puts "&| set $value :|[ expr { [llength [ primesLowerThan [- $value 1 ] ]]*100./ [- $value 1 ] }] |[ expr { ([llength [ primesLowerThan [- 10 1 ] ]]*100./ [- 10 1 ] )/( [llength [ primesLowerThan [- $value 1 ] ]]*100./ [- $value 1 ]) }] | |&" }Applications for proc ::math::quantity_into_ratios
gold 6/3/2021. Professor Joran Firberg outlined a Babylonian partner or brother inheritance problem for 7 brothers sharing the available silver of 100 shekels on tablet, IM31210P2, ref Friberg, A Remarkable Collection of Babylonian Mathematical Texts. Professor Firberg gives the solution as a series of integer numbers < 16 14 12 10 8 6 4 > with the commentary on the Babylonian false shares algorithm. One can see that the sum of the shares sequence as expr { 16 + 14 + 12 + 10 + 8 + 6 + 4 } returns 70 silver shekels. For the TCL calculations, the problem constraints developed a normalized sequence of brother shares or multiple ratios, starting with the eldest brother with largest share as normalized 1. Each younger brother receives a share less or subtracted as rational fraction (1/8 ). In other words, subtract expr { 1/8. } = 0.125 shekel for the next younger brothers share. The second eldest brother would receive a normalized share of expr { 1.-1/8. } = 0.875 shekels, Base_10 decimal. The normalized sequence for each brothers share is < 1. 0.875 .75 .625 .5 .375 .25 > decimal notation. The sum of the normalized sequence for each brothers share is expr { 1. + 0.875 + .75 + .625 + .5 + .375 + .25 }, 4.375. As an alternate algebraic gist of the false shares method, the equation < $false_share * 4.375 = 70 > transposes to $false_share = expr { 70/4.375 }, 16. Use the $false_share of 16 to multiply the normalized sequence for brother shares and the share of eldest brother falls out as expr { 16*1 } = 16, and so on with the younger brothers. Using some alternate calculations on market rates, I posted a Math proc Template called ::math::quantity_into_ratios on the wiki. For the initial available silver of 70 pieces, eval < ::math::quantity_into_ratios 70 1. 0.875 .75 .625 .5 .375 .25 > returns < 16.0 14.0 12.0 10.0 8.0 6.0 4.0 > silver pieces. As a check, the sum of all brothers shares is expr {16.0 + 14.0 + 12.0 + 10.0 + 8.0 + 6.0 + 4.0 }, 70.
gold 6/3/2021. Professor Joran Firberg offered some commentary on a Babylonian partner or brother inheritance problem for 10 brothers sharing the available silver of 100 shekels on tablet, IM31210P7, ref Friberg, A Remarkable Collection of Babylonian Mathematical Texts. The Babylonian mathematicians are showing considerable sophistication is solving some of the constraints with the arithmetic mean. The Babylonian text reported that total of first 3 shares was 46.8 shekels. Collateral inference was that the next to eldest brother share was expr { 46.8 / 3 } = 15.6 shekels. This problem lacked some parts of a complete answer on the tablet, but believe that the available tablet content can be loaded into a provisional TCL solution in Base_10 decimal. For the TCL calculations, the problem constraints developed a normalized sequence of brother shares or multiple ratios, starting with the eldest brother with largest share as normalized 1. Each younger brother receives a share less or subtracted as fraction 0.09302 decimal. In other words, subtract 0.093023 for the next younger brothers share. The second eldest brother would receive a normalized share of expr { 1.- 0.09302 } = 0.906977 , Base_10 decimal. The normalized sequence for each brothers share is < 1. 0.90698 0.8139 0.72094 0.62792 0.5349 0.44188 0.34886 0.25584 0.16282 > decimal notation. The sum of the normalized sequence for each brothers share is expr { 1. + 0.90698 + 0.8139 + 0.72094 + 0.62792 + 0.5349 + 0.44188 0.34886 + 0.25584 + 0.16282 }, 5.8141. As an alternate algebraic gist of the false shares method, the equation < $false_share * 5.8141 = 100 > transposes to $false_share = expr { 100/5.8141 }, 17.1995, rounded to 17.2 shekels. Using some alternate calculations on market rates, I posted a Math proc Template called ::math::quantity_into_ratios on the wiki. For the initial available silver of 100 pieces, eval < ::math::quantity_into_ratios 100 1. 0.90698 0.8139 0.72094 0.62792 0.5349 0.44188 0.34886 0.25584 0.16282 > returns < 17.1997 15.5998 13.9988 12.3999 10.80006 9.20014 7.60022 6.0003 4.40038 2.80046 > silver pieces. As a check, the sum of all brothers shares is expr {17.1997 + 15.5998 + 13.9988 + 12.3999 +10.80006 + 9.20014 + 7.60022 + 6.0003 + 4.40038 + 2.80046}, 99.9997, rounds to 100.
;# code snippet for printing IM31210P7 sequence
set share 1.
set sum 1.
set answer [list ]
foreach val {1 2 3 4 5 6 7 8 9 } {
set share [ expr { $share - 0.09302 } ]
set sum [ expr { $sum + $share } ]
lappend answer $share
}
puts " answer sequence = 1. $answer "
puts " sum $sum "Quadratic Equation Solution from Muller's method
Console wrapper for 2nd order quadratic_solution proc returns the real solution 1 or real solutions 1&2 from quadratic coefficients. Looking for real roots only here, discriminant => 0. Boiled down from evaluating discriminant, there are three possible outcomes from 2nd order quadratic equation as follows: 1) discriminant $discriminant_2 > 0 has two real roots. 2) discriminant $discriminant_2 == 0 has one real root. 3) discriminant $discriminant_2 < 0 has two complex non-real roots. There are some 2nd order solutions that have no real solutions. Note that Muller's method or rearranged 2C formula avoids significant figure problem (somewhat). TCL may use math ops to eval rational fractions or roots as inputs to subroutine for more significant figures. First argument is 3 execution options. option == 1 , return positive solution, option == 2 , return negative and positive solutions , option == 3 , return negative and positive solutions with diagnostics. Need some more testcases for working envelope. Should be loadable into a graphical user interface gui.
Possible sources of error in numerical analysis. References reported potential error in significant figures from subtracting nearly equal quantities in formula. Also, when the two real roots are very close, cancellation may occur between the terms b2 and 4ac of the discriminant. Possibly diagnostics in subroutine should flag when these conditions are approached? With proc entry in arguments $args, it appears that multiple successive 2nd order quadratic equations by three coefficients could be solved with a few code switches.
TCLLIB ticket 5af6381a8be0d5a87505d7e28203fe69fa2b3019 in que, dated 7/3/2021 Title: Quadratic Equation Solution, 2 reals from Muller's method
Reference [L2 ]
The golden ratio constant is used several times on our wiki pages, so the phi or gr constant may be used to check the math template proc. As used in the textbooks, the golden ratio constant is 1.6180339887… and the golden ratio conjugate is 0.6180339887… The golden ratio is the positive solution to the quadratic equation < 1* x**2 - 1*x -1. = 0 > or set of 3 quadratic coefficients < 1 -1. -1. > . The golden conjugate constant is the negative solution here to the quadratic equation. The exact solution for the golden ratio constant is < $gr = expr { ( 1 + sqrt(5))*.5} > or 1.618033988749895. The exact solution for the golden ratio constant is < $grc = expr { ( 1 - sqrt(5))*.5}, -0.6180339887498949. The command to the math template proc < ::math::quadratic_solution 3 1 -1. -1. > returns two solutions < -0.61803398874989479 1.6180339887498947 > , at least accurate to 15 significant figures.
Conclusions
gold Update 7/3/2021. I have found it easier and more tidy to start with a working TCL math template and morf a few lines into a new purpose. If one completes and tests the new TCL subroutine in a console program, then usually one can load the new TCL subroutine into a graphical user interface (gui).
Subroutine Template 1, quantity_into_multiple_ratios
# pretty print from autoindent and ased editor
# quantity_into_ratios for math::stats? package
# working under TCL version 8.6
# console program written on Windows 10 on TCL
# gold on TCL WIKI, 2Mar2017
package require Tk
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
#
# ::math::quantity_into_ratios --
#
# Return the division of quantity by two or more given ratios
#
# Arguments:
# val first value is quantity
# args other values are two or more given ratios
#
# Results: parts of quantity divided by ratios
#
proc ::math::quantity_into_ratios {quantity args} {
set sum 0.
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
foreach val $args {
set sum [ expr { $sum + $val } ]
}
foreach val $args {
lappend answer [ expr { $quantity * ($val/$sum) } ]
}
set answer
}
# end of working deck
# add cosmetics below to bottom of file
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Console wrapper for quantity_into_ratios proc"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " Console wrapper for quantity_into_ratios proc"
puts " Return the quantities from list of ratios"
puts " [ ::math::quantity_into_ratios 84 2 2 2 ] "
puts " for ::math::quantity_into_ratios 84 2 2 2 returns 28.0 28.0 28.0 "
puts " for ::math::quantity_into_ratios 84 1 2 4 returns [ ::math::quantity_into_ratios 84 1 2 4 ] "
puts " for ::math::quantity_into_ratios 84 1 2 4 returns 12.0 24.0 48.0 "
puts " [ ::math::quantity_into_ratios 84 ] << for ::math::quantity_into_ratios 84 returns zero "
#end of deckPrintout for quantity_into_ratios proc
Console wrapper for quantity_into_ratios proc Return the quantities from list of ratios 28.0 28.0 28.0 for ::math::quantity_into_ratios 84 2 2 2 returns 28.0 28.0 28.0 for ::math::quantity_into_ratios 84 1 2 4 returns 12.0 24.0 48.0 for ::math::quantity_into_ratios 84 1 2 4 returns 12.0 24.0 48.0 0 << for ::math::quantity_into_ratios 84 returns zero
Subroutine Template 2, sqrt_sum_of_squares
# pretty print from autoindent and ased editor
# easy eye calculator, large black type on green
# used as testbed for one liners programs
# written on Windows 10 on TCL
# working under TCL version 8.6
# gold on TCL WIKI , 10Sep2020
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
#
# sqrt_sum_of_squares --
#
# Return the sqrt_sum_of_squares by one or more
#
# Arguments:
#
# args other values are one or more
#
# Results: sqrt_sum_of_squares
#
proc math::sqrt_sum_of_squares { args} {
set sum 0.
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
foreach val $args {
set sum [ expr { $sum + $val*$val } ]
}
set answer [ expr { sqrt($sum) } ]
}
#puts " ::math::sqrt_sum_of_squares ( 2 2 2 ) answer [sqrt 12 ]
# 3.4641016151377544
#puts " [ ::math::sqrt_sum_of_squares 1 2 4 ] "
#puts " [ ::math::sqrt_sum_of_squares 2 ] for ( ) returns zero "
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Console wrapper for sqrt_sum_of_squares "}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " sqrt_sum_of_squares 2 2 2 equals [ math::sqrt_sum_of_squares 2 2 2 ]"
puts " sqrt_sum_of_squares 1 1 1 equals [ math::sqrt_sum_of_squares 1 1 1 ]"
puts " sqrt_sum_of_squares 1 1 equals [ math::sqrt_sum_of_squares 1 1 ]"
puts " sqrt_sum_of_squares 1 equals [ math::sqrt_sum_of_squares 1 ]"
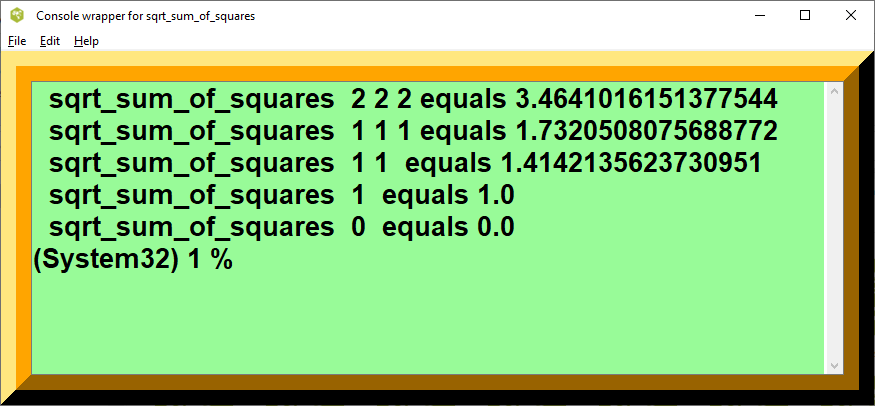
puts " sqrt_sum_of_squares 0 equals [ math::sqrt_sum_of_squares 0 ]"output for sqrt_sum_of_squares
sqrt_sum_of_squares 2 2 2 equals 3.4641016151377544 sqrt_sum_of_squares 1 1 1 equals 1.7320508075688772 sqrt_sum_of_squares 1 1 equals 1.4142135623730951 sqrt_sum_of_squares 1 equals 1.0 sqrt_sum_of_squares 0 equals 0.0
Pseudocode, Equations, and Wiki Page Checklist
#pseudocode can be developed from rules of thumb.
#pseudocode: some problems can be solved by proportions (rule of three), to some order of magnitude
#pseudocode: enter quantity1, quantity2, quantity3 and expected output (quantity4) for testcases.
#pseudocode: enter time in years, number of remaining items
#pseudocode: output fraction of (remaining items) over (items at time zero)
#pseudocode: ouput remaining items as fraction or percent
#pseudocode: output fraction of (quantity4 ) over ( quantity1 at time zero)
#pseudocode: output fraction of (quantity2) * (quantity3 ) over (quantity1 at time zero)
#pseudocode: outputs should be in compatible units.
#pseudocode: rules of thumb can be 3 to 15 percent off, partly since g..in g..out.
#pseudocode: need test cases > small,medium, giant
#pseudocode: need testcases within range of expected operation.
#pseudocode: are there any cases too small or large to be solved?
Subroutine Template 3, geometric_mean
# pretty print from autoindent and ased editor
# geometric_mean for math::stats? package
# working under TCL version 8.5.6 and eTCL 1.0.1
# console program written on Windows XP on eTCL
# gold on TCL WIKI, 2Mar2017
package require Tk
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
console show
# ::math::geometric_mean --
#
# Return the geometric_mean of two or more values
#
# Arguments:
# val first value
# args other values
#
# Results:
# geometric_mean arithmetic geometric_mean value
proc ::math::geometric_mean { args } {
set product 1.
set N [ expr { [ llength $args ] } ]
foreach val $args {
set product [ expr { $product*$val } ]
}
set exponent [ expr { 1./$N } ]
set geometric_mean [ expr { $product**$exponent } ]
#puts " $N $exponent $product $args "
set geometric_mean
}
;# end of working deck
;# add cosmetics below to bottom of file
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Console wrapper for ::math::geometric_mean proc"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " Console wrapper for ::math::geometric_mean proc"
puts " Return the quantities from list of ratios"
puts " ::math::geometric_mean ( 1 2 3 4 ) answer 2.2133638 "
puts " [ ::math::geometric_mean 1 2 3 4 ] answer 2.2133638 "
Subroutine Template 4, list of normalized_set
;# pretty print from autoindent and ased editor
;# normalized_set for math::stats? package
;# working under TCL version 8.6
;# console program written on Windows 10 on TCL
;# gold on TCL Club, 26Jun2021
package require Tk
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
;# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
;#
;# ::math::normalized_set --
;#
;# Return the list of normalized_set by division of selected quantity
;# Arguments:
;# val first value is selected quantity
;# args other values are numbers to be normalized
;#
;# Exemption 1, if input list has 1 or zero entries, return 0
;# >> args of one element, meaning no quanities, return 0
;# Exemption 2, if selected quantity has zero entries, return 0
;# >> remove possibility of division by zero
;# Results: set of normalized numbers divided by selected quantity
;#
;# $sum_? reserved for sums and averages of quantites, not used now
;#
proc ::math::normalized_set {quantity args} {
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
if { $N == 0 } { return 0 }
if { $quantity == 0 } { return 0 }
set quantity [ expr { $quantity * 1. } ]
set sum_entries 0.
set sum_normalized 0.
foreach val $args {
set sum_entries [ expr { $sum_entries + $val } ]
set sum_normalized [ expr { $sum_normalized + $val/$quantity } ]
}
set mean [ expr { $sum_entries * 0.5 } ]
set average_normalized [ expr { $sum_normalized * 0.5 } ]
;# remove comment for sum and mean reports in printout
;# puts " sum_entries $sum_entries entries mean $mean sum_normalized $sum_normalized normalized mean $average_normalized"
foreach val $args {
lappend answer [ expr { $val * (1./$quantity) } ]
}
return $answer
}
;# check with printout >>> puts "check with printout $quantity $args answer $answer"
;# end of working deck
;# add cosmetics below to bottom of file
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Console wrapper for normalized_set proc"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " Console wrapper for normalized_set proc"
puts " ************************** "
puts " Begin test suite "
puts " ************************** "
puts " Return the quantities from list of normalized_set by division of selected quantity"
puts " [ ::math::normalized_set 2 2 2 2 ] "
puts " for ::math::normalized_set 2 2 2 2 returns 1.0 1.0 1.0 "
puts " for ::math::normalized_set 2 1 2 4 returns [ ::math::normalized_set 2 1 2 4 ] "
puts " for ::math::normalized_set 2 1 2 4 returns 0.5 2.0 2.0 "
puts " for ::math::normalized_set 2 1 2 3 4 5 6 7 8 9 10 returns [ ::math::normalized_set 2 1 2 3 4 5 6 7 8 9 10 ]"
puts " for ::math::normalized_set 10. 1 2 3 4 5 6 7 8 9 10 returns [ ::math::normalized_set 2 1 2 3 4 5 6 7 8 9 10 ]"
puts " [ ::math::normalized_set 2 ] << for args set of 1 element ::math::normalized_set 2 returns zero "
puts " [ ::math::normalized_set 0 ] << for ::math::normalized_set 0 returns zero "
;# end of deck Test Suite printout for list of normalized_set
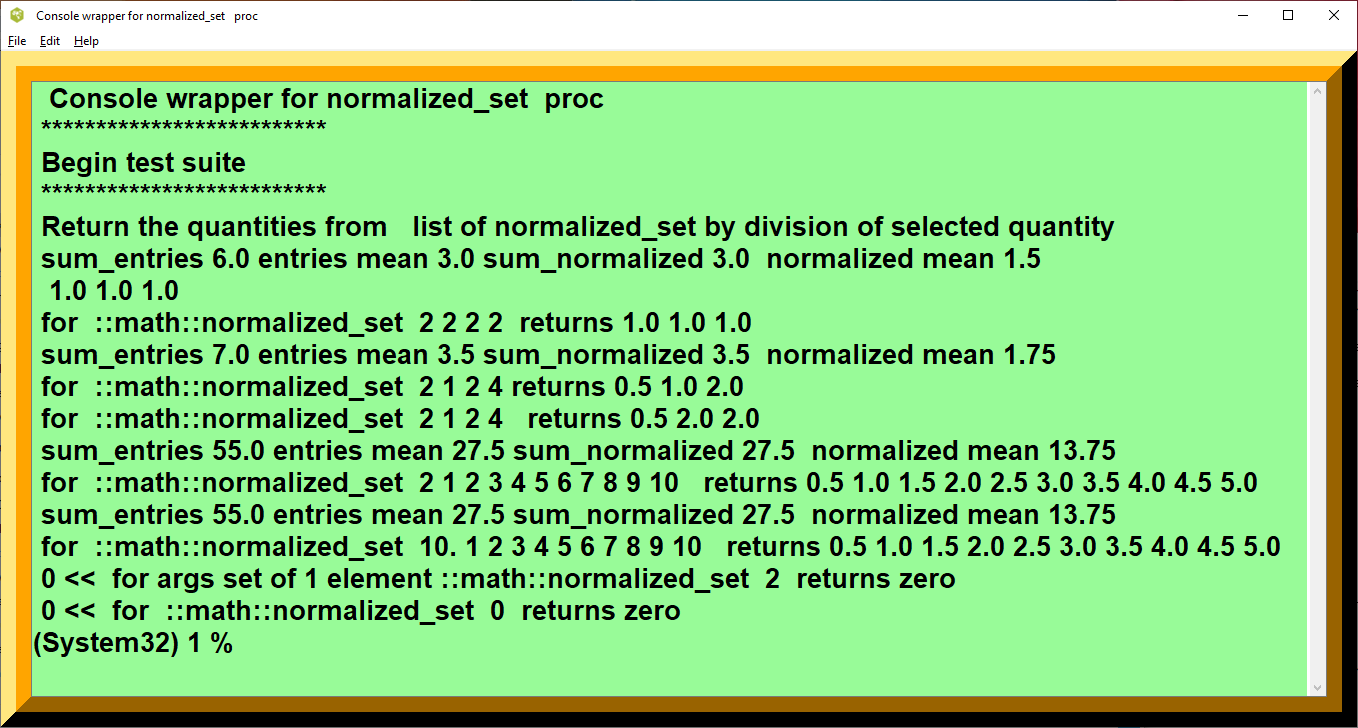
Console wrapper for normalized_set proc ************************** Begin test suite ************************** Return the quantities from list of normalized_set by division of selected quantity sum_entries 6.0 entries mean 3.0 sum_normalized 3.0 normalized mean 1.5 1.0 1.0 1.0 for ::math::normalized_set 2 2 2 2 returns 1.0 1.0 1.0 sum_entries 7.0 entries mean 3.5 sum_normalized 3.5 normalized mean 1.75 for ::math::normalized_set 2 1 2 4 returns 0.5 1.0 2.0 for ::math::normalized_set 2 1 2 4 returns 0.5 2.0 2.0 sum_entries 55.0 entries mean 27.5 sum_normalized 27.5 normalized mean 13.75 for ::math::normalized_set 2 1 2 3 4 5 6 7 8 9 10 returns 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 sum_entries 55.0 entries mean 27.5 sum_normalized 27.5 normalized mean 13.75 for ::math::normalized_set 10. 1 2 3 4 5 6 7 8 9 10 returns 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 0 << for args set of 1 element ::math::normalized_set 2 returns zero 0 << for ::math::normalized_set 0 returns zero (System32) 1 %
Possible Errors, Predefined Entries, Break Lines, Possible Wild_Cards in TCLLIB::math local copy
# Arguments:
# limit1 The limit for the largest prime to be included in the estimate
#
if { $limit1 <= 1 } {
return -code error "The limit must be larger than 1"
}
if { $limit2 <= 1 } {
return -code error "The upper limit must be larger than 1"
}
if { $n == 0 } {return 0}
if { $n < 1 } {return 0}
if { $n == 1 } {return 1}
if {$n<2} then {return -code return 2}
if {$n<4} then {return -code return 4}
if {$n<9} then {return -code return 9}
# forgivable error but no entry forwarded for calculation
if { [ isprime $limit3 ] < 1 } {
break
}
# Add the additional procedures to TCLLIB::math local copy
#
proc ::math::numtheory::call {args} {uplevel catch [list $args]}
proc ::math::numtheory::mathx { args } { set tcl_precision 17; puts [ expr [ expr { $args } ] ] }
;# translating Fortran and Qbasic control flow statements
proc ::math::numtheory::stop {} { return }
proc ::math::numtheory::end {} { exit }
proc ::math::numtheory::pause {} { wait .00010}
;# set comment lines from Fortran
proc ::math::numtheory::C {args} { set C # }
proc ::math::numtheory::REM {args} { set REM # } ;# attack of bots from Qbasic
proc ::math::numtheory::write {args} { puts $args }
proc ::math::numtheory::print {args} { puts $args } ;# attack of bots from Quickbasic
proc ::math::numtheory::SUBROUTINE {args} { proc $args }
proc ::math::numtheory::SUB {args} { proc $args } ;# attack of bots from Quickbasic
;# namespace eval ::math::constants {
variable constants {
pi 3.14159265358979323846 "ratio of circle circumference and diameter"
e 2.71828182845904523536 "base for natural logarithm"
ln10 2.30258509299404568402 "natural logarithm of 10"
phi 1.61803398874989484820 "golden ratio"
phi_2 0.61803398874989484820 "golden ratio conjugate"
tcl_precision_1 17 "tcl_precision number"
) set result {}
;# set list for calculation results
lappend result $number
}
return $resultTestcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program.
Testcase 1
| table testcase 1 | printed in | tcl wiki format | |
|---|---|---|---|
| quantity | value | comment, if any | |
| set_number: | percent of prime numbers in set | percent primes in set of 10 over / set of N | |
| set 10 : | 44.44 | 1.0 | Modern base_10 |
| set 20 : | 42.10 | 1.05 | Archaic IndoEuropean base_20 |
| set 30 : | 34.48 | 1.28 | |
| set 40 : | 30.76 | 1.44 | |
| set 50 : | 30.61 | 1.45 | |
| set 60 : | 28.81 | 1.54 | Babylonian base_60 |
| set 70 : | 27.53 | 1.61 | |
| set 80 : | 27.84 | 1.59 | |
| set 90 : | 26.96 | 1.64 | |
| set 100 : | 25.25 | 1.76 | |
| set 110 : | 26.60 | 1.67 | |
| set 120 : | 25.21 | 1.76 |
Screenshots Section
Screenshots Section
figure 1a. Console wrapper for prime_formula proc
figure 1b, Console wrapper for sqrt_sum_of_squares
figure 1c, Console wrapper for sqrt_sum_of_squares
figure 1d, Console wrapper for normalized_set
figure 1e, Market_Rate_Problem
figure 1e, Gauss Approximate Number of Primes
figure 1f, Golden_Ratio_definition
figure 2.
figure 3.
figure 4.
figure 5.
figure 6.
figure 7.
figure 8.
figure 9.
figure 10.
figure 11.
figure 12.
References:
- Primes
- Oneliner's Pie in the Sky
- One Liners
- Comparing Tcl and Python
- Primes Sieve - on a resizable canvas from uniquename
- TCLLIB ::math::numtheory
- https://en.wikipedia.org/wiki/Prime-counting_function
- http://sweet.ua.pt/tos/primes.html#i
- http://mathworld.wolfram.com/PrimeCountingFunction.html
- http://www.math.uni-bonn.de/people/jbuethe/topics/AnalyticPiX.html
- http://primes.utm.edu/notes/rh.html
- http://numbers.computation.free.fr/Constants/Primes/pixtable.html
- http://numbers.computation.free.fr/Constants/constants.html
- on line prime number generator, see
- http://www.miniwebtool.com/list-of-prime-numbers/?to=50
- Mathematician pair find prime numbers aren't as random as thought, March 15, 2016 by Bob Yirka,
- ref Robert Lemke Oliver and Kannan Soundararajan, Stanford University
- google < Prime number theorem Wikipedia >
- Probability that a number is prime, John D. Cook, 6 October 2010
- Probability of Next Prime Digit, Kevin's Math Page, Kevin Gong,March 17th, 2016
- Mathematicians Discover Prime Conspiracy, Erica Klarreich , March 13, 2016, Quanta Magazine
- Prime Probability: Catch the Wave, Michael M. Ross , Excel spreadsheet, Jan2008
- Prime Numbers and Their Statistical Properties,Dr. Phillip M. Feldman
- 19TH CENTURY MATHEMATICS - GAUSS, The Story of Mathematics
- A Conjecture about the Density of Prime Numbers,
- Lincoln Almir AMARANTE RIBEIRO, Departamento de Física,
- Universidade Federal de Minas Gerais, good explanation
- Dan Rockmore Stalking the Riemann Hypothesis, The Quest to Find the Hidden Law of Prime Numbers
- J. Pintz. On Legendre's prime number formula. Amer. Math. Monthly 87 (1980)
- Dusart, Pierre. Estimates of some functions over primes without r.h
- Ref. proc sum_primes_to by dkf
- from Comparing Tcl and Python on TCL WIKI
- Ref. Sieve of Eratosthenes « Python recipes « = code.activestate.com/recipes/117119/
References:
- Wikipedia search engine < TCL programs >
- Wikipedia search engine < TCL introduction >
- Wikipedia search engine < prime number >
- Google search engine < prime number formulas >
- Seaching for Babylonian Triplets Slot Calculator Example
- Gauss Approximate Number of Primes and eTCL demo example calculator, numerical analysis
- KWJ in Monster Prime Predicting Formula
- http://scidiv.bcc.ctc.edu/math/pythagoras.html
- http://www.saltire.com/applets/pythag/incircle.html
- http://math.uic.edu/~fields/puzzle/triples.html
- http://rle-vlsi.mit.edu/people/gjcoram/triples.html
- http://bsuvc.bsu.edu/home/00lcsapp/maths460.html
- http://www.math.utah.edu/~alfeld/teaching/pt.html
- http://138.25.60.81/numericon/triples.html
- http://www.geom.umn.edu/~demo5337/Group3/ti4.html
- http://www-groups.dcs.st-and.ac.uk/~history/PrintHT/Babylonian_Pythagoras.html
- Daniel F. Mansfield , N.J. Wildberger.
- Plimpton 322 is Babylonian exact sexagesimal trigonometry.
- Historia Mathematica, August 2017 DOI: 10.1016/j.hm.2017.08.001
- Newsweek, Babylonian Tablet Could Hold Mathematical
- Secrets For Today's Researchers, Josh Lowe , 8/25/17
- Unexpected biases in the distribution of consecutive primes
- Robert J. Lemke Oliver, Kannan Soundararajan ,Department of Mathematics, Stanford University
- The Last Digit of Prime Numbers - Numberphile on Youtube
- Lecture on “Rock, paper, scissors in probability, Tadashi Tokieda
- Hardy-Littlewood conjectures.
- MATHEMATICS SCIENCE, A new pattern in primes, Shubashree Desikan, Hindu Times
- en.wikipedia.org wiki search on Tadashi_Tokieda
- https://www.ncbi.nlm.nih.gov articles/PMC4978288/
- Distribution of the units digit of primes, C. M. Ko, National Central University
- www.wired.com tadashi-tokieda-finds-startling-objects-in-plain-sight/
Updating Plimpton 322, Babylonian tablet References:
- The Algorithm of Factor 12:
- Generating the Information Carved on the Plimpton 322 Tablet.
- September 20, 2011, Anthony Phillips, Stony Brook University
- Fernando Quinonez, mentioned available prime numbers on tablet.
- Robert Creighton Buck. Sherlock Holmes in Babylon. Am. Math. Mon., 87:335 – 345, 1980.
- Buck cited prime numbers on Plimpton 322.
- Victor Katz, Robin Wilson - Sherlock Holmes in Babylon and Other Tales of Mathematical History (Spectrum) (2004)
- The Plimpton 322 Tablet and the Babylonian Method of Generating Pythagorean Triples
- by Abdulrahman Ali Abdulaziz, date 2010-03-31
- Words and Pictures: New Light on Plimpton 322
- ELEANOR ROBSON, American Mathematical Monthly 109 (2002), 105-120
- A history of mathematics, Carl Boyer, page 36-37
- Note. Some above B. math references are successfully locked behind paywalls.
;# References ;# current TCLLIB routines in Math Module math::numtheory::numberPrimesGauss N math::numtheory::numberPrimesLegendre N math::numtheory::numberPrimesLegendreModified N math::numtheory::differenceNumberPrimesLegendreModified lower upper math::numtheory::listPrimePairs lower upper step math::numtheory::listPrimeProgressions lower upper step
References on Quadratic Equations:
- wikipedia [L3 ]
- Bhaskara quadratic [L4 ]
- Math proc templates [L5 ]
- xra-slides [L6 ]
- Roots_of_a_quadratic_function [L7 ]
- Babylonian Triplets [L8 ]
- Quadratic_equation [L9 ]
- Quadratic_function [L10 ]
- Polynomial definition [L11 ]
- Cubic_equation [L12 ]
- Quartic_equation [L13 ]
Appendix Code
appendix TCL programs and scripts
Subroutine Template 4, prime_formula
# pretty print from autoindent and ased editor
# easy eye format, large black type on green
# used as testbed for one liners programs
# written on Windows 10 on TCL
# working under TCL version 8.6
# gold on TCL WIKI , 5/15/2021
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
#
# prime_formula --
#
# Return the possible primes in list by one or more
#
# Arguments:
#
# args other values are one or more
#
# Results: prime_formula
#
proc prime_formula { args} {
set list_new [list ]
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
foreach val $args {
lappend list_new [ expr { 16*$val + 15. } ]
}
return $list_new
}
# end of initial deck
# add cosmetics below to bottom of file
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Console wrapper for prime_formula proc"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " Console wrapper for prime_formula proc"
puts " Return the possible primes in list "
puts " formula < 7 11 13 14 > equals possible primes? [ prime_formula 7 11 13 14 ]"
Subroutine Template 5, Combined Market Rate formula
;# pretty print from autoindent and ased editor
;# easy eye console, large black type on green
;# used as testbed for one liners programs
;# written on Windows 10 on TCL
;# working under TCL version 8.6
;# gold on TCL WIKI , 10Sep2020
;# Babylonian Combined Market Rate V6
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
;# adapted from tcl Stats 2011-05-22, arithmetic mean <RLE>
;# ::math::combined_market_rate --
;#
;# Return the combined_market_rate by one,two, or more given rates
;# market rate defined as quantity per price
;# or 1 over (price per quantity)
;#
;# Arguments:
;#
;# args values are one, two, or more given rates
;#
;# Results: combined_market_rate
;# works for positive numbers, negative numbers,
;# and mixed positive & negative numbers.
;# arg of zero returns zero
;# arg of null returns zero
;# filter foreach drops irregular zero elements from argument
proc ::math::combined_market_rate { args} {
set sum 0.
set N [ expr { [ llength $args ] } ]
if { $N == 0 } { return 0 }
if { $N == 1 || [ lindex $args 0 ] == 0 } { return 0 }
set res {};set counter2 0;
;# filter foreach drops irregular zero elements
foreach item $args {if {$item != 0 } {incr counter2 1; lappend res $item } }
set counter 0
foreach val $res {
set sum [ expr { $sum + 1./$val } ]
incr counter 1
}
set combined_market_rate1 [ expr { 1./(($sum*1.)/$counter2) } ]
return $combined_market_rate1
}
;# various testcases on combined_market_rate
;# puts [::math::combined_market_rate 0.5524 0.4807 0.42918 0.47846 ]
;# answer 0.48131 "
;# puts [ ::math::combined_market_rate .1 .2 .3 .4 ]
;# answer 0.192
;# ::math::combined_market_rate -.1 -.2 -.3 -.4
;# answer -0.192, correct
;# operator math formula follows
;# check [/ 1. [/ [+ [/ 1. -.1] [/ 1. -.2] [/ 1. -0.3 ] [/ 1. -0.4] ] 4. ] ]
;# returns -0.192, correct
;# puts " [ ::math::combined_market_rate .1 ] "
;# :math::combined_market_rate -.1 -.2 .3 .4
;# answer -0.4363636363636364
;# operator math formula follows
;# set check [/ 1. [/ [+ [/ 1. -.1] [/ 1. -.2] [/ 1. 0.3 ] [/ 1. 0.4] ] 4. ] ]
;# check equals -0.4363636363636364
;# puts " for (::math::combined_market_rates .1)
;# returns .1 "
;# ::math::combined_market_rate {}
;# null returns zero, correct.
;# ::math::combined_market_rate 0
;# arg 0 returns zero, correct.
;# addition dated 24sep2018
;# added filter foreach to remove zero's
;# irregular zeros,
;# test on zero's 0.1 0.0 0.0 0.2 0.3 0.4
;# returns 0.192 , correct
;# test on zero's 0.1 0.0 0.0 0.2 0.3 0.4
;# returns 0.192 , correct
# end of initial deck
# add cosmetics below to bottom of file
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Console wrapper for combined market rate proc"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " Console wrapper for combined market rate proc"
puts " Return the combined market rate from list "
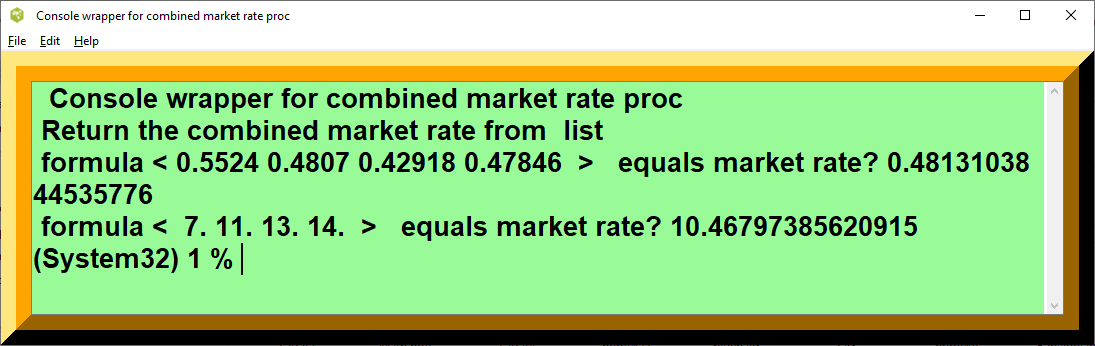
puts " formula < 0.5524 0.4807 0.42918 0.47846 > equals market rate? [ ::math::combined_market_rate 0.5524 0.4807 0.42918 0.47846 ]"
puts " formula < 7. 11. 13. 14. > equals market rate? [ ::math::combined_market_rate 7. 11. 13. 14. ]"Subroutine Template 6, Quadratic Equation Solution, Muller's method
# pretty print from autoindent and ased editor
# quadratic_solution for math::stats? package
# working under TCL version 8.6
# console program written on Windows 10 on TCL
# gold on TCL Club, 2Mar2021
# note rearranged 2C formula avoids significant figure problem
package require Tk
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
#
# ::math::quadratic_solution
#
# Return the possible real solutions of quadratic equation from 3 coefficients
#
# Arguments:
# val first value is option
# args other values are 3 coefficients of quadratic equation
#
# Results: 2 solutions, positive and negative
# looking for real roots only here, discriminant => 0
# option == 1 , return positive solution
# option == 2 , return negative and positive solutions
# option == 3 , return negative and positive solutions with diagnostics
# there are some quadratic equations that have no real solutions.
proc ::math::quadratic_solution {option args} {
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
set option_1 $option
set answer [list ]
set a [lindex $args 0 ]
set b [lindex $args 1 ]
set c [lindex $args 2 ]
set denom_term_1 [ expr { $b*$b-4.*$a*$c } ]
set discriminant_2 [ expr { sqrt ($denom_term_1) } ]
;# looking for real roots only here, discriminant => 0
if { $discriminant_2 < 0 } { return 0 }
set solution_negative [ expr { ( 2.*$c)/( $discriminant_2 - $b) } ]
set solution_positive [ expr { ( 2.*$c)/( -1.*$discriminant_2 - $b) } ]
if { $option_1 == 1 } { lappend answer $solution_positive }
if { $option_1 == 2 } { lappend answer $solution_negative $solution_positive }
if { $option_1 == 3 } {
lappend answer $solution_negative $solution_positive
puts " printout diagnostics "
puts " option number $option_1 ??? =? 3 returns diagnostics "
puts " a [lindex $args 0 ] "
puts " b [lindex $args 1 ] "
puts " c [lindex $args 2 ] "
puts " discriminant_2 $discriminant_2 "
if { $discriminant_2 > 0 } {
puts "discriminant $discriminant_2 > 0 has two real roots "}
if { $discriminant_2 == 0 } {
puts "discriminant $discriminant_2 > 0 has one real root "}
if { $discriminant_2 < 0 } {
puts "discriminant $discriminant_2 < 0 has two complex non-real roots "} }
return $answer
}
# end of working deck
# add cosmetics below to bottom of file
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Console wrapper for quadratic_solution proc"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " Console wrapper for quadratic_solution proc"
puts " Return the quadratic_solution 1 or 1&2 from quadratic coefficients"
puts " for ::math::quadratic_solution 1 1 1.5 -1. returns [ ::math::quadratic_solution 1 1 1.5 -1. ] "
puts " for ::math::quadratic_solution 2 1 1.5 -1. returns [ ::math::quadratic_solution 2 1 1.5 -1.] "
puts " for ::math::quadratic_solution 1 1 2.66666 -1 returns [ ::math::quadratic_solution 1 1 2.66666 -1 ] "
puts " for ::math::quadratic_solution 2 1 2.66666 -1 returns [ ::math::quadratic_solution 2 1 2.66666 -1 ] "
puts " for ::math::quadratic_solution 1 200. -1.5e-12 -1 returns [ ::math::quadratic_solution 1 1 200. -1.5e-12 ] "
puts " for ::math::quadratic_solution 2 200. -1.5e-12 -1 returns [ ::math::quadratic_solution 2 1 200. -1.5e-12 ] "
puts " for ::math::quadratic_solution 1 returns zero returns [ ::math::quadratic_solution 1 ] "
puts " option 3 prints out quadratic diagnostics "
puts " for ::math::quadratic_solution 3 200. -1.5e-12 -1 & diagnostics returns [ ::math::quadratic_solution 3 1 200. -1.5e-12 ] "
puts " TCL may use math ops to eval rational fractions or roots as inputs to subroutine for more significant figures. "
puts " for ::math::quadratic_solution 3 1 <3./2.> -1. returns [ ::math::quadratic_solution 3 1 [/ 3. 2.] -1. ] "
puts " for ::math::quadratic_solution 3 1 <8./3.> -1 returns [ ::math::quadratic_solution 3 1 [/ 8. 3.] -1 ] "
puts " for ::math::quadratic_solution 3 1 <sqrt 5 > -1 returns [ ::math::quadratic_solution 3 1 [sqrt 5.] -1 ] "
puts " ***** golden ratio is positive solution and golden conjugate is negative here ***** "
puts " for ::math::quadratic_solution 3 1 -1. -1. returns [ ::math::quadratic_solution 3 1 -1. -1. ] "
#end of deck
;# end of deckPrintout for Subroutine Template 6, Quadratic Equation Solution, Muller's method
Console wrapper for quadratic_solution proc Return the quadratic_solution 1 or 1&2 from quadratic coefficients for ::math::quadratic_solution 1 1 1.5 -1. returns 0.5 for ::math::quadratic_solution 2 1 1.5 -1. returns -2.0 0.5 for ::math::quadratic_solution 1 1 2.66666 -1 returns 0.3333340000012 for ::math::quadratic_solution 2 1 2.66666 -1 returns -2.9999940000012004 0.3333340000012 for ::math::quadratic_solution 1 200. -1.5e-12 -1 returns 7.4999999999999996e-15 for ::math::quadratic_solution 2 200. -1.5e-12 -1 returns -105.553116266496 7.4999999999999996e-15 for ::math::quadratic_solution 1 returns zero returns 0 option 3 prints out quadratic diagnostics printout diagnostics option number 3 ??? =? 3 returns diagnostics a 1 b 200. c -1.5e-12 discriminant_2 200.00000000000003 discriminant 200.00000000000003 > 0 has two real roots for ::math::quadratic_solution 3 200. -1.5e-12 -1 & diagnostics returns -105.553116266496 7.4999999999999996e-15 TCL may use math ops to eval rational fractions as inputs to subroutine for more significant figures. printout diagnostics option number 3 ??? =? 3 returns diagnostics a 1 b 1.5 c -1. discriminant_2 2.5 discriminant 2.5 > 0 has two real roots for ::math::quadratic_solution 3 1 <3./2.> -1. returns -2.0 0.5 printout diagnostics option number 3 ??? =? 3 returns diagnostics a 1 b 2.6666666666666665 c -1 discriminant_2 3.3333333333333335 discriminant 3.3333333333333335 > 0 has two real roots for ::math::quadratic_solution 3 1 <8./3.> -1 returns -2.9999999999999987 0.33333333333333331 (System32) 1 %
Gamblers_Ruin_Expectation
Gamblers Ruin Expectation E(P(N)) Application to Random Walks
An example from a wildly different subject is the Gamblers Ruin Expectation E(P(N)) application to Random Walks. The Gamblers Ruin Expectation as total probability over all individual N games is considered a part of the Random Walks topics. As defined here, expectation E(P(N)) is the combined probability over 1 or more games with a constant win probability for each game. The example here is 50 percent chance of winning for each game and complement percentage for losing. The Expectation E(P(N)) or Gamblers chance of going broke after N successive games is E(P(N)) = < 0.5 + 0.25 + 0.125 + . . Nth game >. The E(P(N) formula over the total games until finish is formula E(P(N)) = xpr {1. - (1./2.)^*$N} . The more games, the closer the E(P(N)) approaches 1. The Expectation E(P(N) for an infinte set of games is 1, meaning a dead loss over all total games. Check for 1 game is expr {0.5 } returns 0.5. Check for 2 games is expr {0.5 + 0.25 } returns 0.75Check for 3 games is expr {0.5 + 0.25 + 0.125 } returns 0.875 and ''expr { 1. - (1./2.)**3. } returns 0.875. Check for 4 games is expr { 1. - (1./2.)**4. } returns 0.9375. The Gamblers Expectation of win over all games or original flush state at E(P(N)) = 0 is not expected here, but still can not be ruled out.
#
# ::math::Gamblers_Ruin_Expectation
#
# Return the real solution of Gamblers_Ruin_Expectation from 2 entries
#
# Arguments:
# games first value is number of games
# probability_win is win probability , 0.5 in example
#
proc Gamblers_Ruin_Expectation {games probability_win} {
if { $games <1 } {
return -code error "The games must be 1 or larger "
}
expr {(1.-($probability_win**$games))} }
# game 1 0.5 returns 0.5
# game 2 0.5 returns 0.75
# game 3 0.5 returns 0.875
# game 4 0.5 returns 0.9375
# game 3 .14 returns 0.997256Hidden Comments Section
Please place any comments here, Thanks, gold 30Apr2021
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |