Parametric Equation Model Vaporware and TCL demo example calculator numerical analysis
Babylonian Expansion Procedure Algorithm and TCL demo example calculator, numerical analysis
This page is under development. Constructive comments are welcome, but please load any constructive comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 08Jul2020
- Babylonian Expansion Procedure Algorithm and TCL demo example calculator, numerical analysis
- Pseudocode Section
- Testcases Section
- Testcase 1 , !st right sided trapezoid
- Testcase 2 , 2nd case of right sided trapezoid
- Testcase 3 , Bisection of right sided trapezoid
- Testcase 4 , right sided trapezoid
- Testcase 5 , right sided trapezoid from Horoscope software
- Testcase 6 , right sided trapezoid from Horoscope software
- Testcase 7 , 1st Progression of smallest plots & trapezoid fields
- Testcase 8 , 2nd Progression of small trapezoid fields
- Testcase 9 , 3rd Progression of larger trapezoids
- Screenshots Section
- figure 1a.
- figure 1b. Babylonian Astronomy Trapezoid Area Concept & Formulas
- figure 1c. Previous sample of vaporware
- figure 1d., previous sample vaporware
- figure 2.
- figure 3.
- figure 4.
- figure 5.
- figure 6.
- figure 7.
- figure 8.
- figure 9.
- figure 10.
- figure 11.
- figure 12.Babylonian_zigzag_function_for_full_moon_eclipses
- figure 13.Babylonian_step_function_for_full_moon_eclipses
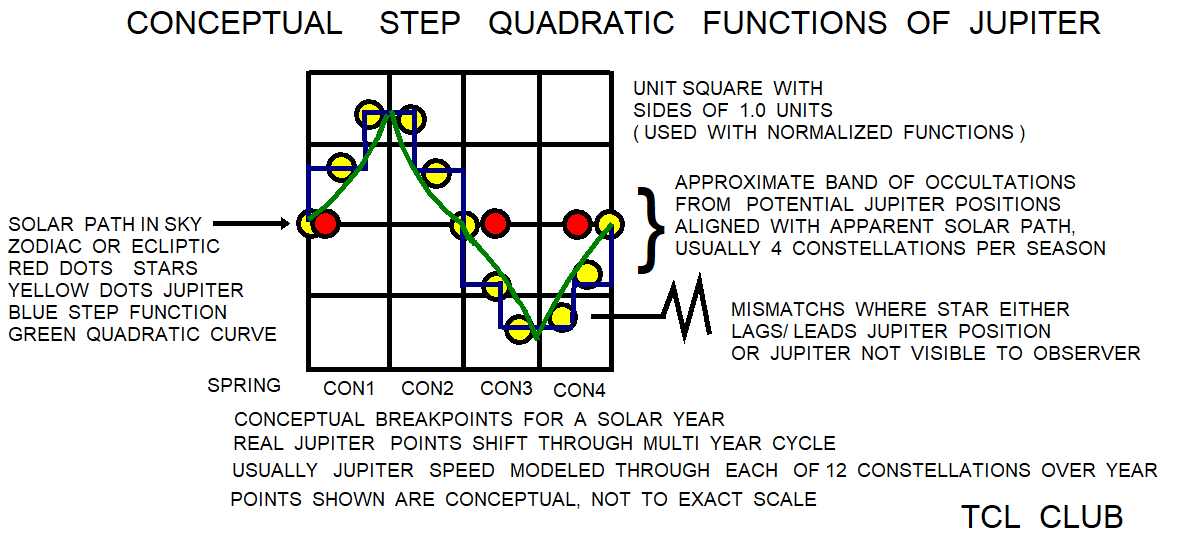
- figure 14.Babylonian_step_functions_with_quadratic_zigzags_overlay_for_Jupiter_occultation_of_star
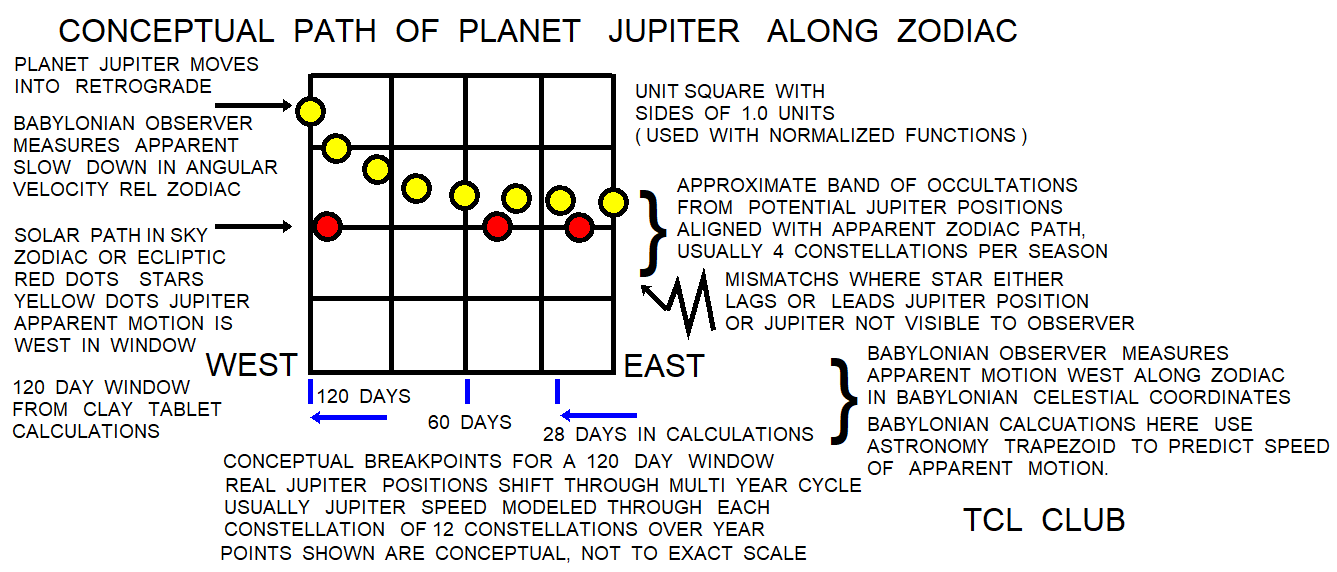
- figure 15.Babylonian_Expansion_Procedure_120_day_chart
- figure 16.Contrast in 2 Different Prediction Algorithms (meaning, 2 possibilities)
- figure 16.quadratic_regression
- figure 17.image of Jupiter taken by NASA's Hubble Space Telescope
- References:
- Testcases Section
- More References
- Appendix Code
- Console program under test.
- printout
- Table of Natural Log and Round_off
- Comments Section
Preface
gold Here are some TCL calculations for Babylonian Expansion Procedure Algorithm in calculator shell. Additional console program below is used to check or improve subroutine.
Introduction
The Babylonian expansion procedure algorithm from clay tablets was loaded into an TCL calculator. The Babylonians did not use algebra notation, so the reader will have to bear some anachronisms in the TCL pseudocode. The expansion procedure is defined as the method used by scribes to estimate the apparent Jupiter angular velocity using the area of Astronomy trapezoids. The bare numbers on the tablets were not usually marked with units or annotated. Successive or iterated math solutions are called algorithms and the expansion procedure is documented form 400 to 600 BCE. The TCL procedures are descendants of this idea. For restating the problem in a computer algorithm, the sides and floor will be in degrees along the Zodiac and days of observation, respectively.
From the references, professor Mathieu Ossendrijver has found some rare Late Babylonian LB clay tablets which estimate the distance that the planet Jupiter travels in 30 or 60 days along the ecliptic or Zodiac using more than one geometric algorithm for the area of a trapezoid. There is some uncertainty in the algorithm steps on individual tablets, but the expansion procedure algorithm for the ecliptic travel can be loaded into a TCL calculator. The analysis is primarily looking at the math reciprocal tablets and the numerical accuracy that would support the expansion procedure algorithm. What would low number reciprocals of high precision be used for? Late Babylonian tablets (300-400 C.E.) have tables of reciprocal numbers from 1 to 2 which are evaluated up to 8 powers of 60, (eg. decimal 0.017777,0.02,0.02083, 0.02222, and 0.026388, not all repeating decimals in base 10 or 60). Some kind of generating function is suggested for large squares or logarithms, meaning squares of 8 digits in base 60. Ref. The powers of 9 and related mathematical tables from Babylon, Mathieu Ossendrijver (Humboldt University, Berlin). One astronomical procedure text, Ossendrijver (2012) Nr. 102, contains several numbers with nine digits.
Babylonian Procedures
The college institutes, textbooks, and computer companies in the USA that previously used the Babylonian mathematical ideas without credit may be glad to know that the Babylonian copyrights and patents expired about 4000 years ago.
In the cuneiform math problems and coefficient lists on clay tablets, there are coefficient numbers which were used in determining the amount of materials and the daily work rates of the workers. In most cases, the math problem is how the coefficient was used in estimating materials, work rates, and math problems. One difficulty is determining the effective magnitude or power of the number coefficient in the base 60 notation. In cuneiform, numbers in base 60 are written on clay tablets using a notation of relative place value. For example, 20 could represent either 20*3600,20*60,20,20/60, 20/3600, or even 1/20. The basic dimensions and final tallies were presented in the cuneiform accounts on clay tablets, but some calculations, some units, and some problem answers (aw shucks!) were left off the tablet. Successive or iterated math solutions are called algorithms and the multiplication methods are some of the earliest algorithms documented, ref the bulk of math tablets were circa 1600 BCE. The TCL procedures are descendants of this idea. The Babylonians did not use algebra notation, decimal notation, or modern units, so the reader will have to bear some anachronisms in the TCL code. At least one approach for the modern reader and using modern terminology is to develop the implied algebraic equations and decimal equivalents from the cuneiform numbers. Then the TCL calculator can be run over a number of testcases to validate the algebraic equations. For the examples of presenting algorithms to modern readers, the calculator shell will give product in modern decimal units. The units can be changed in the internal calculator formulas as TCL code. Any convenient and consistent output units might be used like millimeters, inches, cubits, feet, or dollars to donuts.
For comparison of the Babylonian algorithm(s) with conventional Western methods, TCL code may include redundant procedures, redundant calculation paths, and printout check formulas to compute product, area, check diagnostics, and relative errors.
Many Place Reciprocals have Similarity to Modern Logarithm steps
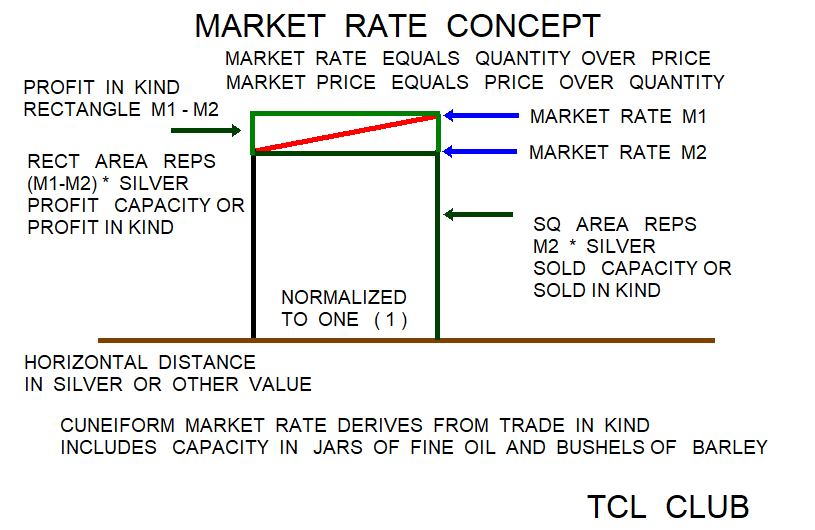
The Babylonian Market Rate Algorithm is taking 1) base_60 reciprocals of several numbers, 2) summing the reciprocals, and 3) using the sum as a multiplication factor. The Market Rate Algorithm has initial steps and similarity to multiplication of several terms using modern logarithms. For example, take the base_60 logarithms of several numbers { 50 40 30 }, resulting in the set { 6/5 6/4 2 }, summing the base_60 reciprocals for a factor expr { 6./5+6./4+2. }, which equals 4.7 decimal. The return reciprocal or anti-reciprocal in base_60 is expr { 60/4.7 } is 12.76 decimal and with a factor approximating average is expr { 3.*60/4.7 } is 38.29787. The average of the original three numbers is expr { (50+40+30.)/3. } or decimal 40.0 For a modern example using natural logarithms, take the problem 50*40*30 = 60000. Take the sum of natural logs as expr { log(50)+log(40)+log(30) } = 11.0020998 decimal. The answer is the antilog expr { 2.718281828**11.0020998 } = 60000. Note: The reciprocal formulas in base_60 are N*R=60, N=60/R, and R=60/N.
In the Late Babylonian period, there were numerous tablets and fragments showing many place reciprocals and factoring other numbers in base_60. The many place reciprocals are reciprocals with 5 to 10 places in base_60. The most unusual tables were many place reciprocals between 1 and 2, ref Friberg and Al-Rawi. Although less common or less extant, there are tables of many place reciprocals between 2 and 4. The square root of sixty is decimal 7.74, so continuing the tables beyond integer 8 would be redundant and not be useful. The tablets with many place reciprocals between 1 and 2 are generated for numbers between 60 and 30. The tablets with many place reciprocals between 2 and 4 are generated for numbers between 30 and 15. Because the Babylonians used relative place notation like a modern slide rule, remember that the calculated many place reciprocals between 60 and 15 could been used in relative base_60 places like 20,20*60,20*3600,20*216000 , and so on.
In addition, there are rare LB. fragments or tables that have numbers in reciprocal pairs in base_60 with the added glyph ibsi, which means either square or square root, ref Friberg and Al-Rawi. In a general sense on other tablets, the term ibsi is associated with square roots, cube roots, raising a number in exponent, or the reverse, but the term ibsi linked with reciprocals is curious. The minimal conclusion is that the Late Babylonian mathematicians considered the regular base_60 reciprocals involved with squares, square roots, or powers. A complete explanation of the many place reciprocal tables is not available, but it has been proven that the many place reciprocals and square tables were used in school copying exercises, school multiplication assignments, and factoring algorithms. There are two multiplication formulas from the Old Babylonian tablets that used differences, sums, and squares. With a squint eye of the amateur, the Old Babylonian tables with many place reciprocals in base_60 look somewhat like the many place numbers (meaning digits) in the modern tables for decimal and natural logarithms.
Testcases are important in development of TCL programs.
In planning any software, it is advisable to gather a number of testcases to check the results of the program. Here, a TCL slot calculator is being used as a testbed for the Babylonian Astronomy Trapezoid Area procedures. The results of the testcases are estimated using the hand calculator and then checked in the slot calculator. Pseudocode and equations are developed from the hand calculations and theory. Small console programs are written to check or proof the alternate subroutines or procedures, rather than keeping the unblessed code and comment lines in the main slot calculator. Finally the improved or alternate subroutines are loaded into the slot calculator. The TCL slot calculator is effectively a shell program to input entries, retain loaded standard testcases, host calculation routines, and display results. Additional significant figures are used to check the TCL calculator, not to infer the accuracy of inputs and product reports. Four significant figures is considered sufficient for most engineering projects.
Most of the testcases involve experiments or models, using assumptions, and rules of thumb. For the push buttons in the TCL calculator, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console to conventional texteditor. For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers should be cleared either on the clear button or on the next solve button.
Discussion
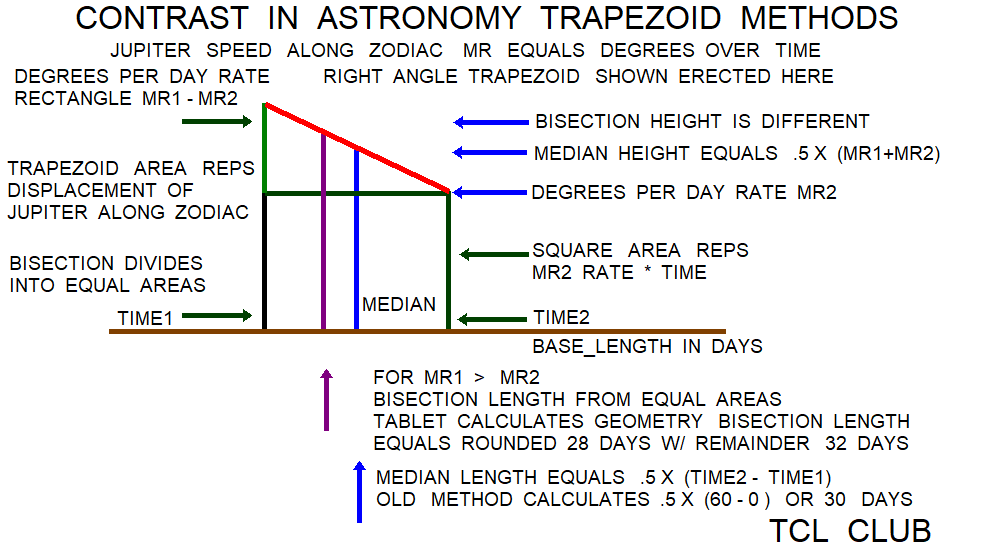
The first testcase has a difference of 2 days in the estimates between median of 30 days and the trapeziod bisection result of 28 days rounded. As listed on the clay tablet, the average speed in degrees per day was approximately 10/60 + 45/3600 or 0.1791 decimal over the total 60 day period between 12/60 and 9/60 degrees per day in base_60. So multiplying the average speed by 2 days suggests an effective Zodiac travel of 0.35 degrees difference between the two methods.
[ expr { (10./60. + 45./3600.) } ] # = 0.1791 decimal degrees per second
[ expr { (12./60. + 9./60.)*.5 } ] # = 0.175 degrees per second motion along Zodiac
[ expr { 2.*(12./60. + 9./60.)*.5 } ] # = 0.35 degrees travel along Zodiac over 2 daysThe extant portions of the cited Astronomy procedure texts are usually very terse, spotty, and need a lot of backgound for understanding. The significant figures used in the Astronomy tablets draw some tentative conclusions. The tablet BM 34676 has astronomy procedures with the planet Mars. The tablet BM 34676 has the translated phrase with 7 significant figures “ appearance <station> 4;59,22,55,57,46,40 <degrees? editor> <as> middle <figure>.” This was a number approximately of 4.985 decimal with the integer of 4 and fraction at 6 significant figures at 59,22,55,57,46,40 in base_60. The Babylonian observation error on the apparent position and motion of the planets was probably about 2 significant figures at most in base_60. Also some unrelated astronomy tablets use 3 significant figures as fractions of degree. The BM 35564 tablet has lunar procedures which develop incremental calculations in multiplying a number of 6 significant figures by a number of 4 significant figures. Since the Babylonian Astronomy group used reciprocal tables, it is thought that the Astronomy reciprocal tables and off tablet multiplication methods would need at least one or two more significant figures to support the Astronomy procedure texts. From the extant portions of the cited Astronomy procedure texts, it is suggested that any postulated Astronomy reciprocal tables and abacus would need about 7 or 8 significant figures in base_60, conservatively. Reference: Babylonian Mathematical Astronomy Procedure Texts by Mathieu Ossendrijver, Berlin, 02/14/2012.
The hand techniques that the Babylonian Astronomers used to measure sky angles is not well known to the later amateurs. However, the Babylonian Astronomy diaries record the angular measurements of stars in cubits and susi. In some older tablet translations, susi are translated fingers. There are either 20 or 24 susi in a cubit depending on the era of the tablet. The clay tablets also record some calculations using Us < literally water> or 4 minutes of time. An Us or one unit of the water clock is equivalent to one modern degree of angle. One cubit in the sky for celestial angles is equivalent to 2 Us or 2 degrees. Using proportions, a Babylonian susi or finger might be about (1 cubit)/(24 susi)*(2 degrees) / (1 cubit) or < expr (1./24.)*(2./1. > or 0.083 degree. 6 fingers would be < expr (1./24.)*(2./1. )*6.> or 0.5 degrees.
One possible hand technique to measure sky angles is to hold a straight edge or ruler at arms length and parallel to the to the heavens. For the modern observer, the sun or moon is convenient standard of 5 degrees across the disc. For example on a given night, if a star is observed 4 lunar discs from the moon, then the equivalent angle would be < expr 4*5. > or 20 degrees. If one takes a blank wooden ruler of about 1 foot and marks the apparent lunar disc in successions across the ruler, that ruler might give some rough measure of sky angles. With a little patience and dodging summer mosquitoes, one can further divide one or two of the successive lunar markings into fifths for a degree mark. Both the ancient Babylonian and Egyptians had both hand rulers and measuring rods marked in cubits, so this possible hand technique seems likely. Actually with a little experience, a single human finger width at arms reach is about 2 degrees. Or combined finger joints of an out stretched hand against the sky can give a rough angle measurement.
A little more speculative for possible use in Babylonian Astronomy, but another hand technique possibility is the use of wooden, metal, or ivory sighting tube or alidade. Even without lenses, a sighting tube can offer significant eye relief in observing a star from the glare of the sky and nearby moon. The possible sighting tube would particularly effective in observing the inner planets and stars when near the horizon. Further, the aperture of the sighting tube would give another rough angle measurement. References. Evidence for an instrumental meaning of ina libbi, NABU 2010, No. 44, 51, by Mathieu Ossendrijver.Babylonian Astronomers and Angular Measure, physics.unlv.edu jeffery. The Vedic Astronomers used stick, nalika tube, and thread for diurnal rising and setting of Sum, Moon, and planet at time of rising or setting.
Sets or Sequences of Geometric Figures
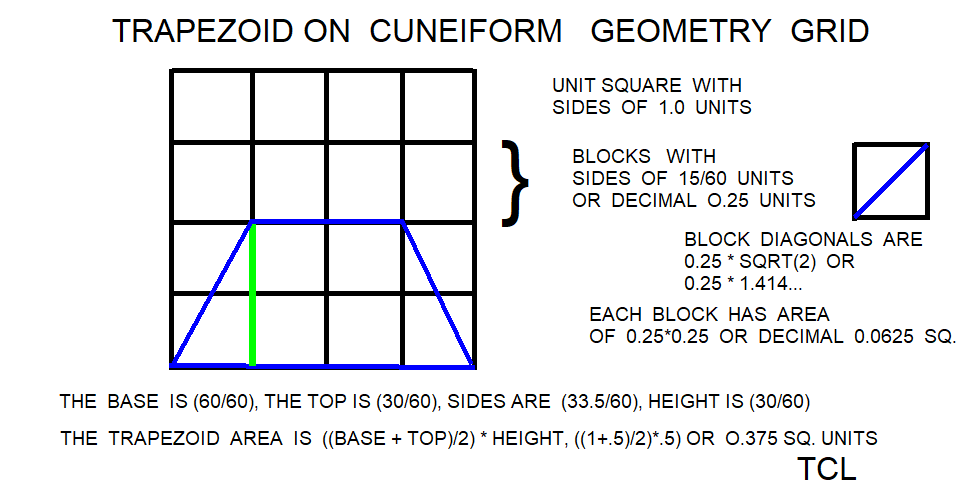
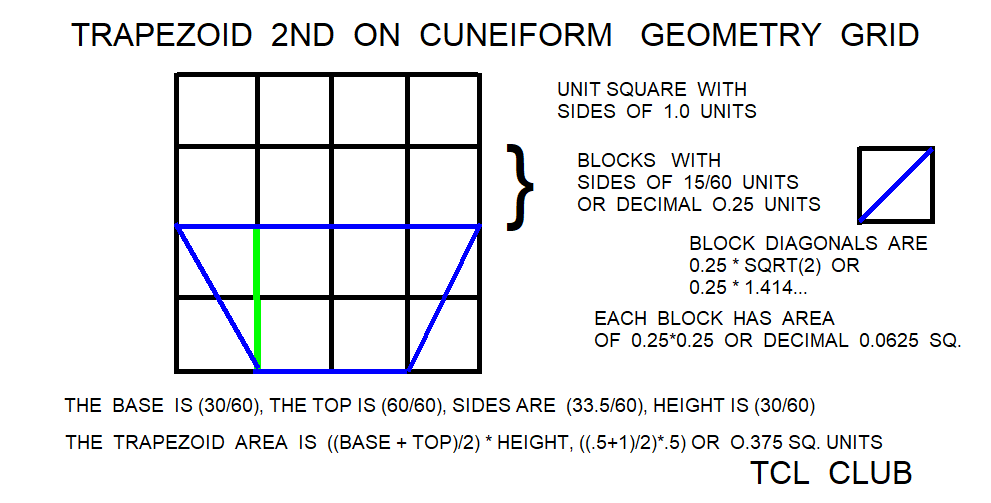
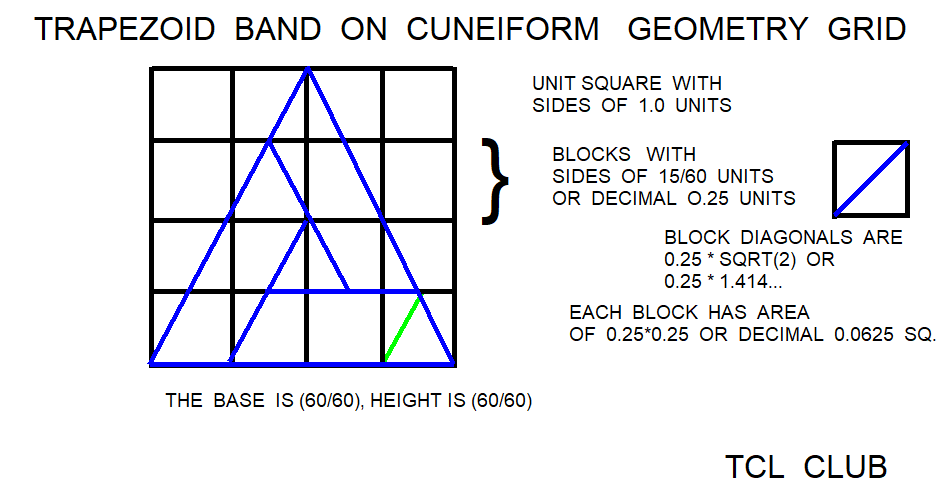
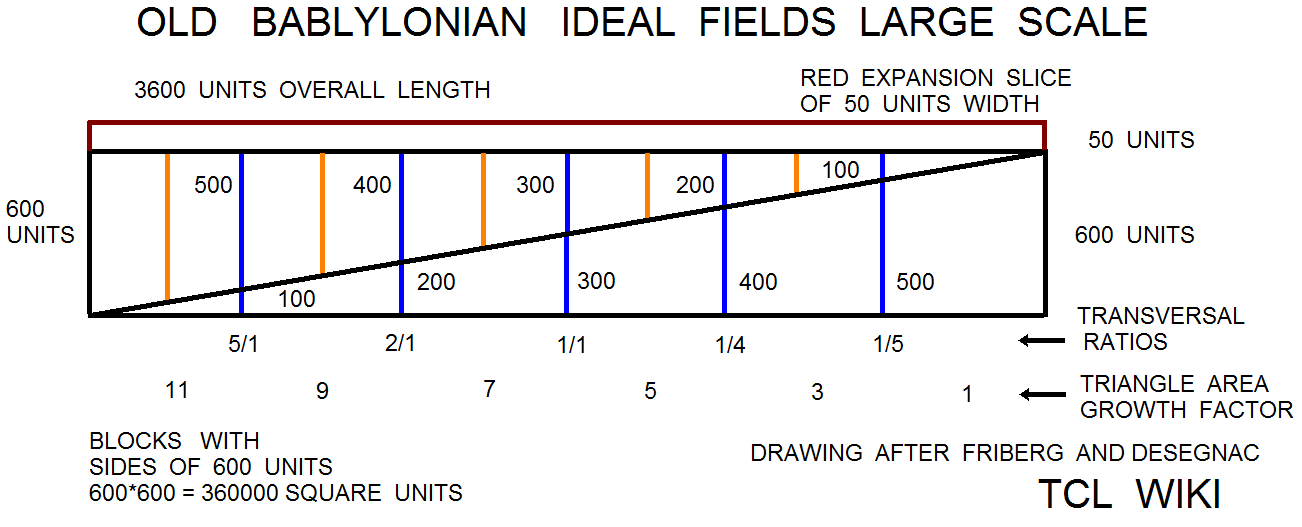
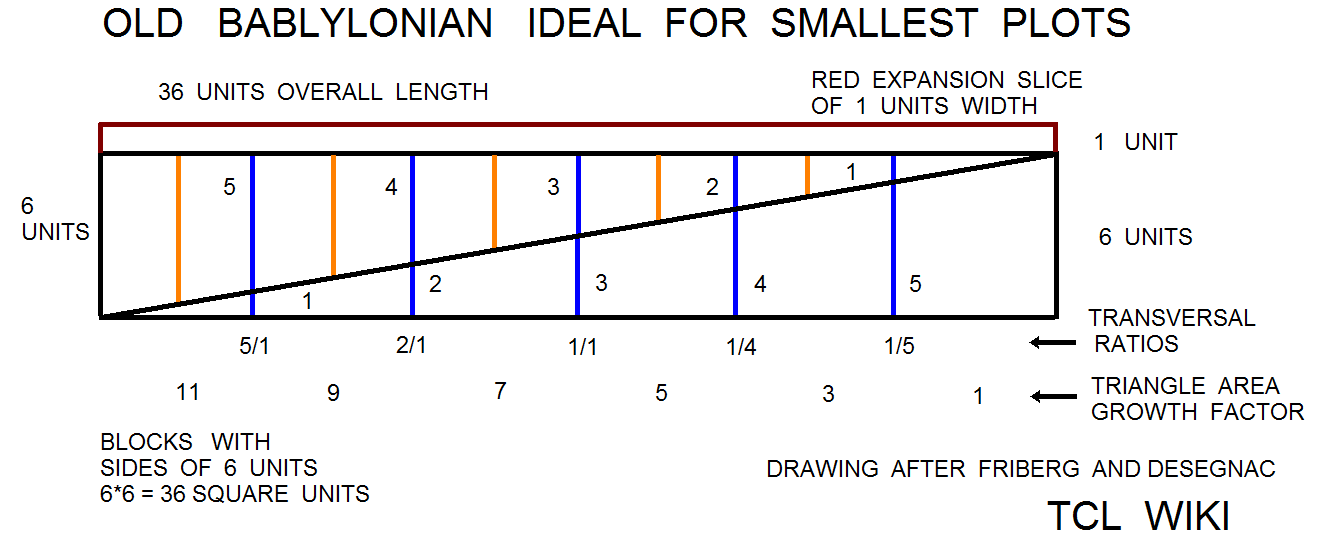
The linguists have found a number of geometry problems that are an set or sequence of geometric figures like triangles, squares, circles, and trapezoids that grow in size. Possibly one can adapt the from an arithmetic sequence for the Brothers Inheritance Algorithm to a geometric sequence or more complex formula. The reported growth sequence over one set of triangles was <1 3 5 7 11 >. This is an arithmetic sequence since there is a common difference between each term. In this case, adding 2 to the previous term in the sequence gives the next term. The ratio sequence in triangle growth would be < 3/1 5/3 7/5 11/7 >. These math problems would be quite a daring challenge for the Babylonian Base_60 system of regular numbers that contain factors of 2,3, and 5. Note that the growth sequence were prime numbers and ratios of prime numbers. In some cases, the geometric growth problems are written as brothers or soldiers receiving plots of land that increase or decrease in size. the trapezoid progressions were studied in the Astronomy Trapezoid Calculator to study the trapezoid progression, as well as to provide additional testcases.
Conclusions
Professor Mathieu Ossendrijver has identified that the Babylonian Astronomy Trapezoids procedures may have been associated with the logic stages of Babylonian market rate predictions. Given the flexibility of the TCL gui code previously posted on this WIKI, some sort of Babylonian market rate predictions and commodity predictions could be gimmicked into the TCL calculator. Pure speculation, but there is evidence that the arithmetic procedures and accuracy of reciprocal tables were sufficient places for tracking Jupiter and other Babylonian Astronomy needs. Meaning these and similar trapezoid area methods were known to cuneiform mathematicians for a 1000 years before the Astronomy Trapezoid texts. Hence there must be some other factor for using the trapezoid geometry methods here with Jupiter. Iffy and if, the Babylonian Astronomy group that were using the trapezoid geometry methods for tracking Jupiter may have been further associated with Babylonian market rate predictions. Look at the market rate charts below, because the Babylonian market rate algorithm has a trapezoid analogy also. The planet Jupiter has a apparent maximum diversion of 1.8 degrees from the Zodiac ecliptic path. The inner planets before Jupiter have greater apparent diversions from the Zodiac path, and probably Jupiter is most aligned to a one dimensional scheme along the Zodiac path. Be interesting if the LB linguists could show that the the Babylonian Astronomy Trapezoids have similar cuneiform terminology and glyphs to the Babylonian Market Rate predictions. Possibly, playing the Babylonian commodity markets took higher digit and many place reciprocals for multiplication than the routine Astronomy calculations.
The TCL calculator seems to be working as it stands.
Pseudocode Section
# using pseudocode for Babylonian expansion procedure algorithm.
# Professor Mathieu Ossendrijver is jumping through 5 different procedures
# for area of trapezoid and right angle trapezoid.
# Conventional formulas for trapezoid area from
# The other Wiki articles use conventional meters on all four sides.
# The Babylonian astronomy procedures use the sides and floor
# in degrees along the Zodiac and days of observation, respectively.
# possible problem instances include add 1/60 to sides until area goal reached
long_side = supplied value
short_side = supplied value
desired_goal = supplied value
# desired_goal usually 100 square units in some early math problems
set old_field_area = a*b , old field_area = long_side * short_side
set new_side_a = long_side + 1/60
set new_side_b = short_side + 1/60
set new_field_area = (long_side + 1/60) * ( short_side + 1/60 )
is new_field_area =? desired_area within +/- (1/60) , yes = finished loop
check error , abs (desired_goal - new_field_area) <= [/ 1. 60.]
half area = area * .5
quarter area = area * .25
check_answer new area =? desired goal , desired goal reached (yes/no)
set answers and printout with resulting values
formulas
following includes algebraic expressions,
terms, and notation
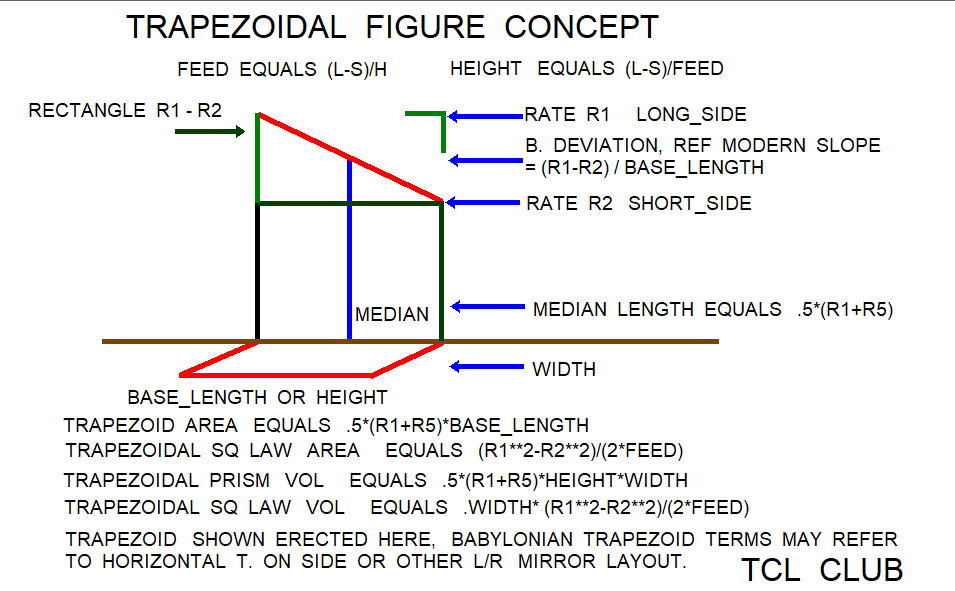
Western trapezoid formulas
and trapezoidal prism volume
following includes algebraic expressions,
terms, and notation not used on tablets
side_aa refs top, t. on side
side_bb refs bottom, t. on side
side_cc refs height, t. on side
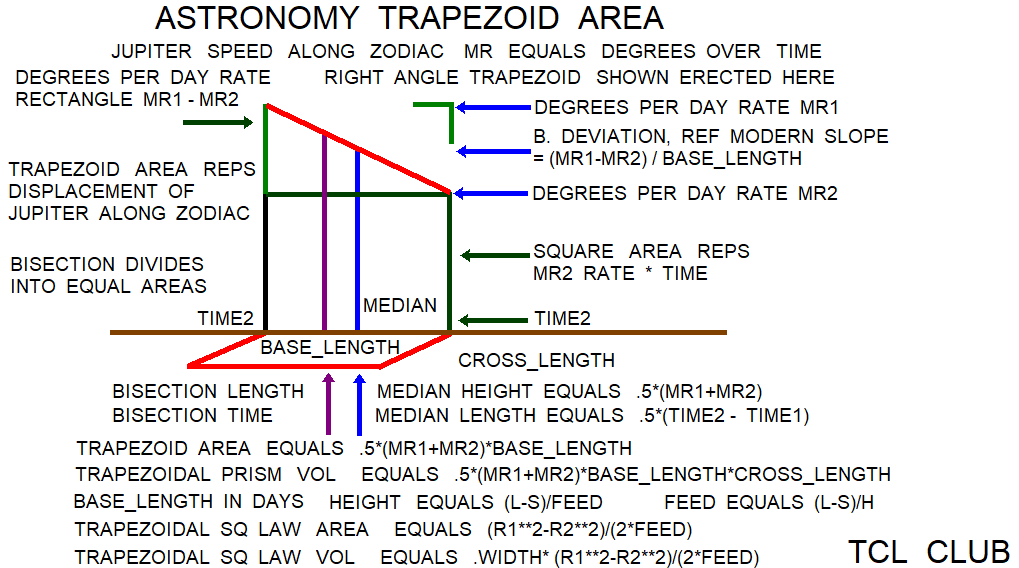
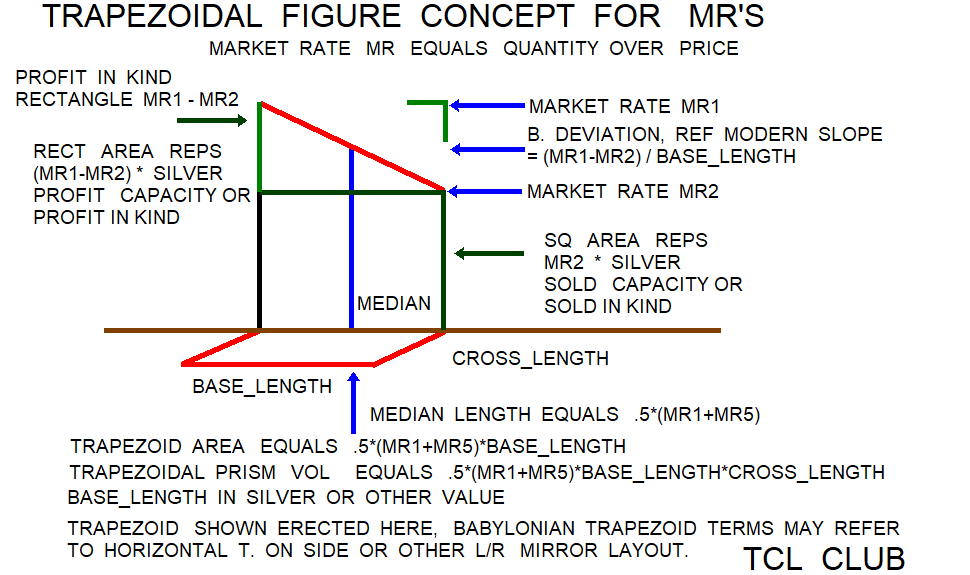
median_length = .5*(side_aa+side_bb)
trapezoid_area= 0.5*(side_aa+side_bb)*height
trapezoid_area= median*height
trapezoidal_prism_volume=
t. vol=length*(0.5*(side_aa+side_bb))*height
median divides equal side lengths
Equations reference
1) median = .5*(l+s) conventional
2) trapezoid area = .5*(l+s)*h conventional
3) feed = (l-s)/h trapezoid_area_sq_law
4) h = (l-s)/feed trapezoid_area_sq_law
5) trapezoid area = (l**2-s**2)/(2.*feed) trapezoid_area_sq_law
# Also, the B. square rule for trapezoid area
# was extended to volumes by *width factor.
6) trapezoidal volume = .5*(l+s)*h*w conventional
7) trapezoidal volume = w*(l**2-s**2)/(2.*feed) trapezoid_area_sq_law
# cribbed code from quad page
set perimeter [+ $side1 $side2 $side3 $side4 ]
set reference_factor [/ [+ [* $side1 $side1 ] [* $side2 $side2 ]] [+ [* $side3 $side3 ] [* $side4 $side4 ]]]
if { $reference_factor > 1.1} { set flag 1. }
if { $reference_factor < 0.9} { set flag 1. }
set semip [* $perimeter .5 ]
set cyclic_quad_area [sqrt [* [- $semip $side1 ] [- $semip $side2 ] [- $semip $side3 ] [- $semip $side4 ]]]
set approx_quad_area [* [* .5 [+ $side1 $side3 ]] [* .5 [+ $side2 $side4 ] ] ]
# >>>> mean speed theorem follows <<<<<
# mean_speed_1 defined apparent velocity of Jupiter along Zodiac in degrees per day
# mean_speed_1 = [ expr { .5 * (velocity_1 + velocity_0 )} ]
# distance = mean speed * time in days, distance in total degrees (Babylonian us units)
# time in days = distance / mean speed
# time in days = [ expr { 5.659086123394399/(.5*(12./60+10./60+49./3600+20./21600) )} ]
# "exact solution time " = 29.690614589584406 days
# base_60 rounding in text a
# time in days = [ expr { (5.+22./60+30./3600)/(.5*(12./60+10./60+49./3600+20./21600) )} ]
# time = 28.200145737187267, rounded to 28 in text a
# end of file, pseudocode: # file, pseudocode:
# lunar coefficients
set mean_interval_b_eclipse [ expr { 223. / 38 } ] # = 5.868421052631579
set lunar_progress_per_synodic_month [ expr { 180. / 5.868421052631579 } ] # = 30.672645739910315
total progress of the moon in 223 synodic months [ expr { 223.* 30.672645739910315 } ] # = 6840.0
mean interval between eclipse [ expr { 6840.0/360 } ] # = 19.0
complete revolution in each of the 223 months [ expr { 19.+223 } ] # = 242.0
mean interval between eclipse
[ expr { (38. * 180. * 223.) / (223.* 360.) } ] # = 19.0
length of the draconitic month i [ expr { (6585.+(20./60)) / (242.) } ] # = 27.21212121212121
length of a synodic month [ expr { (6585.+(20./60)) / (223.) } ] #= 29.53064275037369
length of 235 months (= 19 years): [ expr { (29.53064275037369 ) * (235.) } ] # = 6939.701046337817
mean motion in longitude [ expr { ( 360. / 27.21212121212121) } ] # = 13.229398663697106 deg per day
# [ expr { $shu+$na+$me+$ge } ] # = function sigma
l sid. month [ expr { ( 1240.+17./60.) / 45. } ] # = 27.561851851851852
235 = 19 years + extra =239 [ expr { ( 6585.+20./60.) / ( 27. + 33./60.) } ] # = 239.03206291591044
l sid. month [ expr { ( 6585.+20./60.) / ( 239.) } ] # = 27.553695955369594 Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
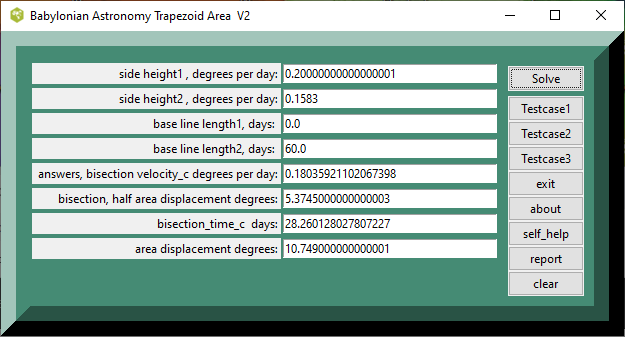
Testcase 1 , !st right sided trapezoid
The following scenario was used for the first testcase from the tablet translation text A of Professor Mathieu Ossendrijver . The first testcase figure was 2 right sided trapezoids in succession. The numbers in base_60 were height1 = ;12 degrees per day, height2 = ;9_30 degrees per day, height3 = ;5_30 degrees per day, length1 = 0 days start, length2 = 1.0; days, and length3 =2.0; days. The given answers were 10:45 degrees per day for the first trapezoid and 5;30 degrees per day for the second trapezoid in base_60. The calculations in the TCL gui is going to output decimal numbers, so conversion will be necessary at some point. In TCL. Using decimal fractions in base_10, the given answers were 10+ 45/60 degrees per day for the first trapezoid as 10.75 decimal The second trapezoid was 5 + 30/60 degrees per day as 5.5 decimal. The converted calculation_1 was expr (.5 *( 12./60 + (9./60+30./3600 )) * 60.) as 10.75 decimal. The converted calculation_2 was [ expr { .5 *( 12./60 + (9./60+30./3600 )) * 60. }] as 5.5 degrees. Based on extant math procedure texts, the baseline or observation period in the trapezoid computations had basewidth examples of 28,30,32, 60, and 120 days, extant envelope was 0 < baseline1 <120 days.
| table 1 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 0.200 : | side height1 , degrees per day: | |
| 0.1583 : | side height2 , degrees per day: | |
| 0.0 : | base line length1, days: | |
| 60.0 : | base line length2, days: | |
| 0.1803 : | answers, bisection velocity_c degrees per day: | |
| 5.3745 : | bisection, half area displacement degrees: | |
| 28.2601 : | bisection_time_c days: | |
| 10.749 : | area displacement degrees: |
Notes: 1st trapezoid area = [ expr { .5 *( 12./60 + (9./60+30./3600 )) * 60. }], decimal 10.75 degrees
bisection velocity_c degrees per day: = [ expr { (((12./60)**2 +(9./60+30./3600)**2)/2.)**.5 }] = 0.18037384018261138
area displacement degrees: = [ expr { 0.18037384018261138*60. }] = 10.822430410956683
bisection_time_c days = [ expr { 60*(v0 - vc)/(v0 - v60) }] and t2 = 60 - tc = 32 days
set bisection_velocity_c [ expr { ((($velocity_0)**2 +($velocity_1)**2)/2.)**.5 }]
set bisection_time_c [ expr { $base_line * ( $velocity_0 - $bisection_velocity_c ) / ( $velocity_0 - $velocity_1 ) }]
Script should be pastable into Easy Eye TCL Console.Testcase 2 , 2nd case of right sided trapezoid
| table 2 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 0.1583 : | side height1 , degrees per day: | |
| 0.0250 : | side height2 , degrees per day: | |
| 60.0 : | base line length1, days: | |
| 120.0 : | base line length2, days: | |
| 0.11332230583605331 : | answers, bisection velocity_c degrees per day: | |
| 2.749 : | bisection, half area displacement degrees: | |
| 20.245 : | bisection_time_c days: | |
| 5.498 : | area displacement degrees: |
Notes. mean speed over second trapezoid = [ expr { (0.2+0.1583 )*.5 }] = 0.17915 decimal
2nd trapezoid area = [ expr { .5 *( 12./60 + (9./60+30./3600 )) * 60. }], decimal 5.5 degrees
Script should be pastable into Easy Eye TCL Console.Testcase 3 , Bisection of right sided trapezoid
The following scenario was used for the second testcase from the tablet translation texts A,B,C,D,&E of Professor Mathieu Ossendrijver. The LB texts are fragmented, so the second testcase is more a compilation of texts A,B,C,D,&E using incomplete broken lines and the LB math terminology on the extant tablets. The second testcase appeared to be bisecting a right sided triangle from the first testcase numbers and using the first right sided trapezoid above. There is some uncertaincy in the extant texts to the amateur eye, including whether the testcase 2 is really meant as a right sided trapezoid or some other 4 sided figure. However, the TCL calculator can adapted with some subroutines or forked calculation paths for either a right sided trapezoid or 4 sided approximation. The numbers in base_60 were height1 = ;12 degrees per day, height2 = ;9_30 degrees per day,length1 = 0 days start, and length2 = 1.0; days.
| table 3 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 0.2 : | side height1 , degrees per day: | |
| 0.0250 : | side height2 , degrees per day: | |
| 0. : | base line length1, days: | |
| 120. : | base line length2, days: | |
| 0.1425 : | answers, bisection velocity_c degrees per day: | |
| 3.375 : | bisection, half area displacement degrees: | |
| 39.4135 : | bisection_time_c days: | |
| 6.75 : | area displacement degrees: |
# time in days = distance / mean speed
# time in days = [ expr { 5.659086123394399/(.5*(12./60+10./60+49./3600+20./21600) )} ]
# "exact solution time " = 29.690614589584406 days
# base_60 rounding in text a
# time in days = [ expr { (5.+22./60+30./3600)/(.5*(12./60+10./60+49./3600+20./21600) )} ]
# time over 1st bisection = 28.200145737187267, rounded to 28 days in text a
# time over 2nd bisection was [ expr { 60-28 } ] = 32 days in text a
# Notes. Script should be pastable into Easy Eye TCL Console.Testcase 4 , right sided trapezoid
| table 4 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 4: | testcase_number | |
| 0.200 : | side height1 , degrees per day: | |
| 0.0250 : | side height2 , degrees per day: | |
| 0.0 : | base line length1, days: | |
| 120.0 : | base line length2, days: | |
| 0.142 : | answers, bisection velocity_c degrees per day: | |
| 3.375 : | bisection, half area displacement degrees: | |
| 39.413 : | bisection_time_c days: | |
| 6.75 : | area displacement degrees: |
Testcase 5 , right sided trapezoid from Horoscope software
The following scenario was used for the _th testcase. There is Astrology software available to derive some testcases from modern numbers. It turns out that the year 2020 offers an interesting retrograde of Jupiter in astrology.
The following scenario was used for the fifth testcase. May get messy, but Professor Mathieu Ossendrijver has identified that the Babylonian Astronomy Trapezoids have been associated with logic stages of Babylonian market rate predictions. Given the flexibility of the TCL gui code previously posted on this WIKI, some sort of Babylonian market rate predictions and commodity predictions could be gimmicked into the TCL calculator. Pure speculation, but there is evidence that the arithmetic procedures and accuracy of reciprocal tables were sufficient tracking Jupiter and other Babylonian Astronomy needs. Hence the Babylonian Astronomy group that were using the trapezoid geometry methods for Jupiter may have been further associated with Babylonian market rate predictions. Look at the market rate charts below, because the market rate algorithm has a trapezoid analogy also. Be interesting if the LB linguists could show that the the Babylonian Astronomy Trapezoids have similar cuneiform terminology and glyphs. Possibly, playing the Babylonian commodity markets took higher digit and many place reciprocals for multiplication than the routine Astronomy calculations.
| Jupiter table | printed in | tcl format | |||
|---|---|---|---|---|---|
| date | time | comment, if any | |||
| 5: | testcase_number | ||||
| 1/1/2020 | 11:06 AM | Speed: | 172% | (0°13'49'' per day) | positive motion |
| 2/1/2020 | 11:06 AM | Speed: | 162% | (0°13'01'' per day) | positive motion |
| 3/1/2020 | 11:06 AM | Speed: | 137% | (0°10'59'' per day) | positive motion |
| 4/1/2020 | 11:06 AM | Speed: | 92% | (0°07'23'' per day) | positive motion |
| 5/1/2020 | 11:06 AM | Speed: | 30% | (0°02'24'' per day) | positive motion |
| 6/1/2020 | 11:06 AM | Speed: | -41% | (-0°03'21'' per day) | retrograde motion |
| 7/1/2020 | 11:06 AM | Speed: | -90% | (-0°07'16'' per day) | retrograde motion |
# Notes
[ expr { 13./60+49./3600 } ] = 0.23027777777777778
[ expr { 10./60+59./3600 } ] = 0.18305555555555555
[ expr { 2./60+24./3600 } ] = 0.04
[ expr { -3./60-21./3600 } ] = -0.05583333333333334 in retrograde
[ expr { -7./60-16./3600 } ] = -0.12111111111111111 in retrograde
# Notes. Script should be pastable into Easy Eye TCL Console.| table 5 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 5: | testcase_number | |
| 0.230 : | side height1 , degrees per day: | |
| 0.183 : | side height2 , degrees per day: | |
| 0.0 : | base line length1, days: | |
| 120.0 : | base line length2, days: | |
| 0.208 : | answers, bisection velocity_c degrees per day: | |
| 6.206 : | bisection, half area displacement degrees: | |
| 56.556 : | bisection_time_c days: | |
| 12.412 : | area displacement degrees: |
Testcase 6 , right sided trapezoid from Horoscope software
The following scenario was used for the 6th testcase. There is Astrology software available to derive some testcases from modern numbers. It turns out that the year 2020 offers an interesting retrograde of Jupiter in astrology.
| table 6 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 6: | testcase_number | |
| 0.183 : | side height1 , degrees per day: | |
| 0.040 : | side height2 , degrees per day: | |
| 0.0 : | base line length1, days: | |
| 120.0 : | base line length2, days: | |
| 0.132 : | answers, bisection velocity_c degrees per day: | |
| 3.345 : | bisection, half area displacement degrees: | |
| 42.414 : | bisection_time_c days: | |
| 6.690 : | area displacement degrees: |
Testcase 7 , 1st Progression of smallest plots & trapezoid fields
| Table 1 | 1st Progression of smallest plots & trapezoid fields | printed in | tcl format | ||
|---|---|---|---|---|---|
| quantity | value | value | value | value | comment, if any |
| area | bisection_time | short_side | long_side | width | comment, if any |
| 3 | undefined | 1 | 0 | 6 | really a right triangle, area=0.5*b*h |
| 9 | 25.13 | 1 | 2 | 6 | begin right trapezoids |
| 15 | 27.029 | 2 | 3 | 6 | |
| 21 | 27.867 | 3 | 4 | 6 | |
| 27 | 28.338 | 4 | 5 | 6 | |
| 33 | 28.639 | 5 | 6 | 6 | |
| >>>>> total area of geometric figures <<<<< | |||||
| 108 | undefined | 6 | 0 | 36 | large right triangle, area=0.5*b*h |
Notes.
set total_sum [ expr { 3+9+15+21+27+33. } ] # = 108.0
Script should be pastable into Easy Eye TCL Console.Testcase 8 , 2nd Progression of small trapezoid fields
| Table 2 | 2nd Progression of small trapezoid fields | printed in | tcl format | ||
|---|---|---|---|---|---|
| quantity | value | value | value | value | comment, if any |
| area | bisection_time | short_side | long_side | width | comment, if any |
| 300 | undefined | 10 | 0 | 60 | really a right triangle, area=0.5*b*h |
| 900 | 25.13 | 10 | 20 | 60 | begin right trapezoids |
| 1500 | 27.029 | 20 | 30 | 60 | |
| 2100 | 27.867 | 30 | 40 | 60 | |
| 2700 | 28.338 | 40 | 50 | 60 | |
| 3300 | 28.639 | 60 | 60 | ||
| >>>>> total area of geometric figures <<<<< | |||||
| 10800 | undefined | 60 | 0 | 360 | large right triangle |
Notes.
set total_sum [ expr { 300+900+1500+2100+2700+3300. } ] # = 10800.0
Script should be pastable into Easy Eye TCL Console.Testcase 9 , 3rd Progression of larger trapezoids
| Table 3 | 3rd Progression of larger trapezoids | printed in | tcl format | ||
|---|---|---|---|---|---|
| quantity | value | value | value | value | comment, if any |
| area | bisection_time | short_side | long_side | width | comment, if any |
| 3000 | undefined | 100 | 60 | really a right triangle, area=0.5*b*h | |
| 9000 | 25.13 | 100 | 200 | 60 | begin right trapezoids |
| 15000 | 27.029 | 200 | 300 | 60 | |
| 21000 | 27.867 | 300 | 400 | 60 | |
| 27000 | 28.338 | 400 | 500 | 60 | |
| 33000 | 28.639 | 500 | 600 | 60 | |
| >>>>> total area of geometric figures <<<<< | |||||
| 108000.0 | undefined | 600 | 0 | 360 | large right triangle, area=0.5*b*h |
Notes.
set total_sum [ expr { 3000+9000+15000+21000+27000+33000. } ] # = 108000.0
Script should be pastable into Easy Eye TCL Console.Screenshots Section
figure 1a.
figure 1b. Babylonian Astronomy Trapezoid Area Concept & Formulas
figure 1c. Previous sample of vaporware

figure 1d., previous sample vaporware
figure 2.

figure 3.
figure 4.
figure 5.
figure 6.
figure 7.
figure 8.
figure 9.
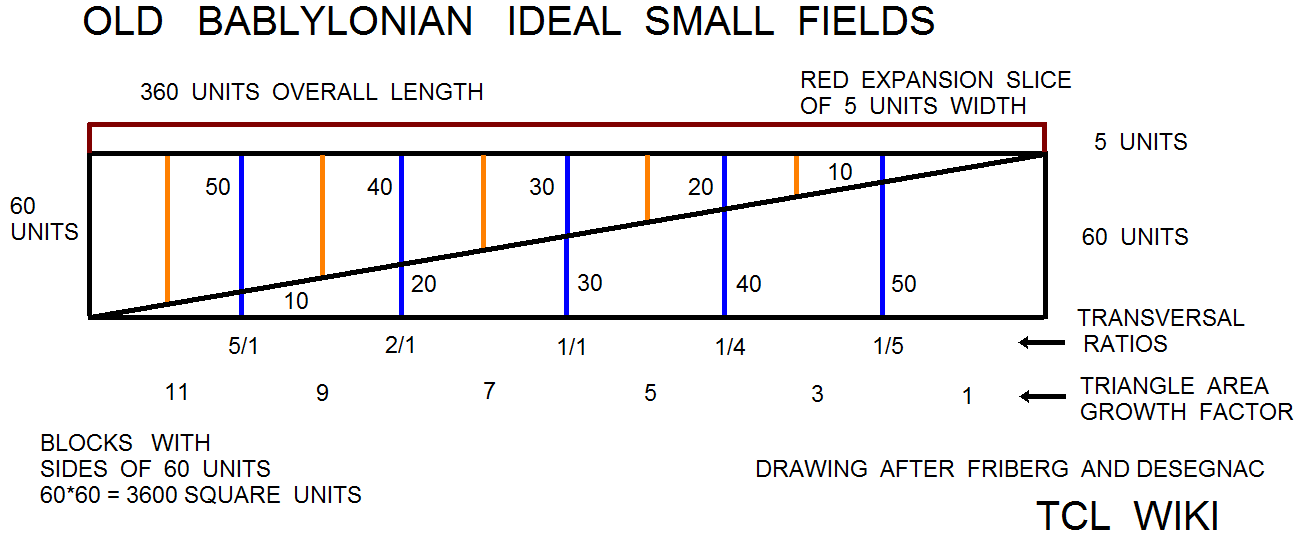
figure 10.
figure 11.
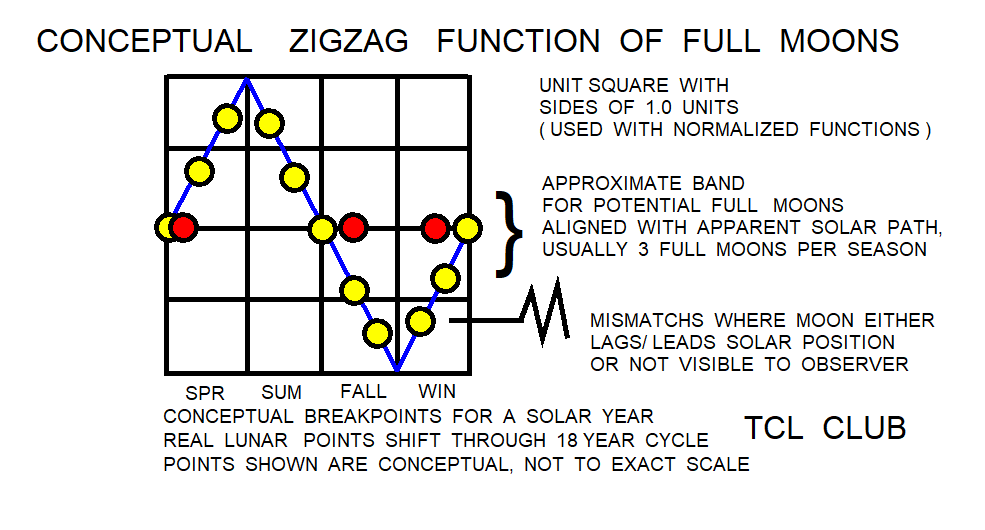
figure 12.Babylonian_zigzag_function_for_full_moon_eclipses
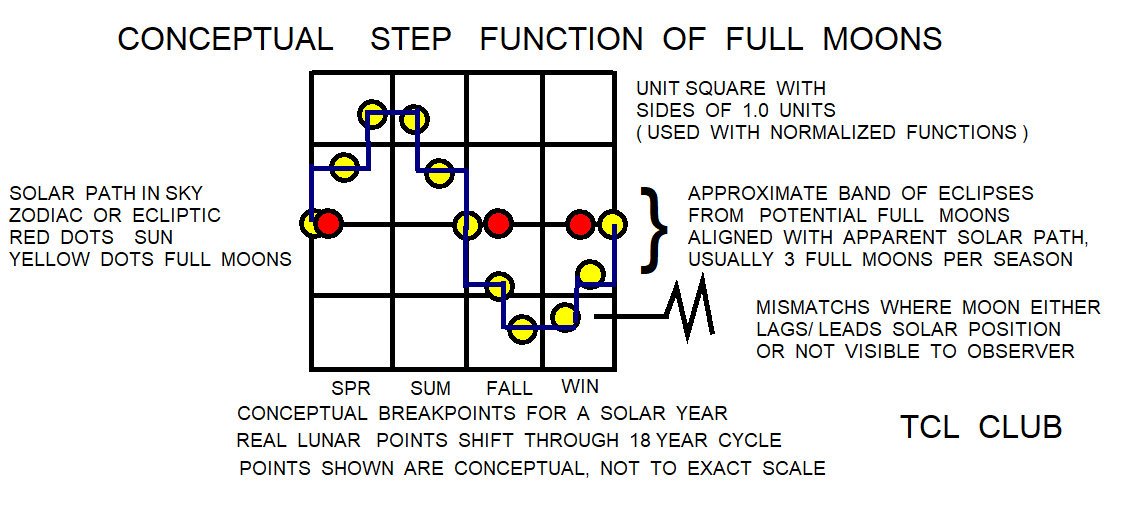
figure 13.Babylonian_step_function_for_full_moon_eclipses
figure 14.Babylonian_step_functions_with_quadratic_zigzags_overlay_for_Jupiter_occultation_of_star
figure 15.Babylonian_Expansion_Procedure_120_day_chart
figure 16.Contrast in 2 Different Prediction Algorithms (meaning, 2 possibilities)
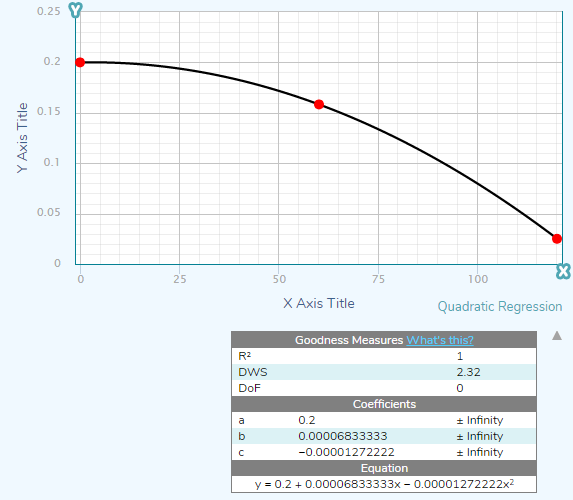
figure 16.quadratic_regression
0 0.2
60 0.1583
120 0.0250 figure 17.image of Jupiter taken by NASA's Hubble Space Telescope
References:
- A Geometric Algorithm with Solutions to Quadratic Equations
- in a Sumerian Juridical Document from Ur III Umma
- Joran Friberg, Chalmers University of Technology, Gothenburg, Sweden
- Geometric division problems, quadratic equations, and recursive
- geometric algorithms in Mesopotamia,Joran Friberg
- google search engine <Trapezoid area bisection>
- Wikipedia search engine <Trapezoid area >
- mathworld.wolfram.com, Trapezoid and right trapezoid
- Mathematical Treasure: Old Babylonian Area Calculation, uses ancient method
- Frank J. Swetz , Pennsylvania State University
- Wikipedia, see temple of Edfu, area method used as late as 200 BC in Egypt.
- Oneliner's Pie in the Sky
- One Liners
- Category Algorithm
- Babylonian Number Series and eTCL demo example calculator
- Brahmagupta Area of Cyclic Quadrilateral and eTCL demo example calculator
- Babylonian Trapezoid Bisection Algorithm and eTCL demo example calculator, numerical analysis
- Chinese Horse Race Problems from Suanshu, DFP, and example eTCL demo calculator, numerical analysis
- Gauss Approximate Number of Primes and eTCL demo example calculator
- Land surveying in ancient Mesopotamia, M. A. R. Cooper
- Sumerian Approximate Area Quadrilateral and eTCL Slot Calculator Demo Example , numerical analysis
- Thomas G. Edwards, Using the Ancient Method of False Position to Find Solutions
- Joy B. Easton, rule of double false position
- Vera Sanford, rule of false position
- www.britannica.com, topic, mathematics trapezoid
- Sumerian Equivalency Values, Ratios, and the Law of Proportions with Demo Example Calculator
- Babylonian Sexagesimal Notation for Math on Clay Tablets in Console Example
- Babylonians Tracked Jupiter With Advanced Tools: Trapezoids, Michael Greshko, news.nationalgeographic.com
- Geometry in Babylonian Astronomy, Cluster of Excellence Topology, Humboldt University of Berlin
- Mathieu Ossendrijver: „Ancient Babylonian astronomers calculated Jupiter’s position
- from the area under a time-velocity graph“, in: Science, January 29, 2016.
- Late Babylonian Field Plans in the British Museum, books.google.com/books
- Karen Rhea Nemet-Nejat
- Late Babylonian Surface Mensuration Author(s): Marvin A. Powell Source: jstor
- translation: trapezoid in two babylonian astronomical cuneiform
- texts for jupiter (act 813 & act 817) from the seleucid era , 310 BC -75 AD
- Otto Neugebauer, Astronomical Cuneiform Texts, 3 Vols.
- Lund Humphreys, London, 1955:405,430-31.
- DeSegnac, MS 3908 A RE-CONSTRUCTION, D.A.R. DeSegnac
- A draft for an essay
- DeSegnac, MENTAL COMPUTING OF THREE ARCHAIC
- MESOPOTAMIAN PUZZLES W 20044, 35, W 20044, 20 & W 20214, essay draft
- DeSegnac, HARMONY OF NUMBERS I and II, D.A.R. DeSegnac, A draft for an essay
More References
- The Marduk Star Nēbiru, Immanuel Freedman,Cuneiform Digital Library Bulletin 2015:3, 8 November 2015
- Computing planetary positions - a tutorial with worked examples, webpage By Paul Schlyter, Stockholm, Sweden
- New perspective on the Exaltation of Planets, Blog of Kiril Stoychev, Bulgarian Astrological Association, December
- 20, 2015
- Probability for Lunar Occultation, for maximum distance from the ecliptic, note by dotancohen, Apr 7 2014,
- Mathematics Stack Exchange
- Babylonian Mathematical Astronomy, Chapter, January 2015, Mathieu Ossendrijver, Freie Universität Berlin
- Babylonian Market Predictions, Chapter on April 2019, Mathieu Ossendrijver, Freie Universität Berlin
- BM 32339+32407+32645 - New Evidence for Late Babylonian Astrology.
- Chapter on September 2018, Mathieu Ossendrijver,
- Freie Universität Berlin
- Ancient Babylonians took first steps to calculus, article By Ron Cowen, Science magazine, 29Jan2016
- Ancient Babylonian astronomers calculated Jupiter’s position from the area under a time-velocity graph,
- Article by Mathieu Ossendrijver, Science magazine, 29Jan2016
- Babylonian mathematical astronomy procedure texts, bibliography
- Babylonian astronomy, Wikipedia, collected 2020
- Babylonian and Indian Astronomy: Early Connections, Subhash Kak, February 17, 2003
- Electrical & Computer Engineering, Louisiana State University, Baton Rouge, LA
- Babylonian Trapezoid Bisection Algorithm and eTCL demo example calculator, numerical analysis
- Babylonian Field Expansion Procedure Algorithm and example demo eTCL calculator, numerical analysis
- Article by Mathieu Ossendrijver, mathematical terminology in Babylonian astronomical texts, 2012
- Babylonian False Position Algorithm and eTCL demo example calculator, numerical analysis
- Babylonian Combined Market Rates and eTCL demo example calculator, numerical analysis
- Babylonian Brothers Inheritance Problems Algorithm and eTCL demo example calculator, numerical analysis
- Babylonian Cubic Equation Problem and eTCL demo example calculator, numerical analysis
- Sumerian Base 60 conversion and eTCL demo example calculator, numerical analysis
- Aryabhat Sum of Squares and Cubes and eTCL demo example calculator, numerical analysis
- Sumerian Approximate Area Quadrilateral and eTCL Slot Calculator Demo Example , numerical analysis
- Article by Mathieu Ossendrijver, Babylonian-computational-astronomy-print.pdf, 2012
- Babylonian Astronomy in Context,
- Keeping the Watch: Babylonian Astronomical Diaries and More, Mathieu Ossendrijver
- Humboldt University Berlin, April 3 2018
- Exploring Jupiter: The Astrological Key to Progress, Prosperity & Potential,
- 310 Pages , 1996 by Stephen Arroyo
- A Primer on Logarithms by Shailesh Shirali, Mathematical Marvels Universities Press
- Studies on the Ancient Exact Sciences in Honor of Lis Brack-Bernsen, eds John M. Steele
- Mathieu Ossendrijver
- A study of Babylonian planetary theory, subtitle The outer planets, by Teije de Jong1
- date 31 August 2018
- Under One Sky: Astronomy and Mathematics in the Ancient Near East
- Author(s): John M. Steele, Annette Imhausen, Publisher: Ugarit-Verlag, Year: 2002
- Rising Time Schemes in Babylonian Astronomy, Author(s): John M. Steele, Publisher: Springer, Year: 2017
- Observation, theory and practice in late Babylonian astronomy: Some preliminary observations, Author(s): Steele J.
- Ancient astronomy and celestial divination, Author(s): N M Swerdlow
- The Babylonian theory of the planets, Author(s): Noel M. Swerdlow,
- Publisher: Princeton University Press, Year: 1998
- Administrative Timekeeping in Ancient Mesopotamia, Robert Englund,
- Journal of the Economic and Social History of the Orient 31 (1988) 121-185
- Bisectable Trapezia in Babylonian Mathematics, Lis Brack Bernsen,Olaf Schmidt
- First published: April 1990
Table, Math Terms Associated with Babylonian Trapezoids
| Table , Math Terms Associated with Babylonian Trapezoids | printed in tcl format | modern equivalent, English | comment if any | |
|---|---|---|---|---|
| sag ki.gu : | side earth | trapezoid | ||
| sag ki.ta : | side earth its , possessive case | upper front of the trapezoid | ||
| sag an.na : | side upper | upper front of the trapezoid | ||
| us gi.na : | length front | true length of the trapezoid | ||
| sag gi.na : | side front | true front of trapezoid | ||
| N1 kus i-ku-lu : | N1 cubit in eats it (it or man), read left to right | feed parameter of the trapezoid | noun derived from Sumerian SOV phrase | |
| sag du : | side | triangle | ||
| N1 arakarum : | N1 multiply | transformation coefficient, usually scale up |
Note. These Math Terms cover 4 or 5 cuneiform languages, and 5000 years of history. Math Terms are best understanding of context and math connotation here,not blessed by linguists and cuneiform dictionaries.
Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# Babylonian Astronomy Trapezoid Area V2
# written on Windows 10 on TCL
# working under TCL version 8.6
# gold on TCL Club, 4Jul2020
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {side height1 , degrees per day:} }
lappend names {side height2 , degrees per day:}
lappend names {base line length1, days: }
lappend names {base line length2, days: }
lappend names { answers, bisection velocity_c degrees per day:}
lappend names { bisection, half area displacement degrees:}
lappend names { bisection_time_c days:}
lappend names { area displacement degrees:}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Babylonian Astronomy Trapezoid Area V2
from TCL ,
# gold on TCL Club, 10Jul2020 "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg "Calculator for Babylonian Astronomy Trapezoid Area V2
from TCL ,
# self help listing
# 4 givens follow.
1) side height1 , degrees per day
2) side height2 , degrees per day
3) base line length1, days
4) base line length2, days
The solution from the clay tablets
is genuine antique method from 1600 BCE
and different looking from modern math methods.
# The Babylonians did not use modern algebraic notation,
# so the reader will have to bear some anachronisms in the TCL code.
# Comparing conventional formula(s) for trapezoid area
# to Babylonian square rule for trapezoid area.
# For comparison, code will include redundant paths & formulas
# to compute trapezoid area. The calculator uses modern
# units for convenience to modern users and textbooks.
# Any convenient and consistent in/output units might be used
# like inches, feet, nindas, cubits, or dollars to donuts.
# Equations
1) median = .5*(l+s) conventional
2) trapezoid area = .5*(l+s)*h conventional
3) feed = (l-s)/h trapezoid_area_sq_law
4) h = (l-s)/f trapezoid_area_sq_law
5) trapezoid area = (l**2-s**2)/(2.*feed) trapezoid_area_sq_law
# Also, the B. square rule for trapezoid area
# was extended to volumes by *width.
6) trapezoidal volume = .5*(l+s)*h*w conventional
7) trapezoidal volume = w*(l**2-s**2)/(2.*feed) trapezoid_area_sq_law
# Recommended procedure is push testcase and fill frame,
# change first three entries etc, push solve,
# and then push report. Report allows copy and paste
# from console to conventional texteditor. For testcases
# testcase number is internal to the calculator and
# will not be printed until the report button is pushed
# for the current result numbers.
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK 8.6 license terms.
# Editorial rights retained under the TCL/TK license terms
# and will be defended as necessary in court.
Conventional text editor formulas or grabbed from internet
screens can be pasted into green console.
Try copy and paste following into green screen console
set answer [* 1. 2. 3. 4. 5. ]
returns 120
# gold on TCL Club, 10jul2020 "
tk_messageBox -title "About" -message $msg }
# following proc is not used now
proc trapezoid_solution { long_side short_side feed width} {
global trapezoid_area height_calc feed_calc median trapezoidal_vol
set median [* .5 [+ $long_side $short_side ]]
set height_calc [/ [- $long_side $short_side] $feed ]
set trapezoid_area [/ [- [* $long_side $long_side] [* $short_side $short_side] ] [* 2. $feed ] ]
set trapezoidal_vol [* $width [/ [- [* $long_side $long_side] [* $short_side $short_side] ] [* 2. $feed ] ]]
set feed_calc [ expr { ($long_side-$short_side)/ $height_calc } ]
puts " check $long_side $short_side $feed height_calc= $height_calc area= $trapezoid_area feed= $feed_calc "
return $trapezoid_area }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set side5 1.
set side6 1.
set side7 1.
set side8 1.
set velocity_0 $side1
set velocity_1 $side2
set base_line [ expr { abs ( $side4 - $side3 )} ]
set calculation_1 [ expr { .5 * ( $side1 + $side2 ) * 60. } ]
set bisection_1 [ expr { .5 * $calculation_1 } ]
set bisection_velocity_c [ expr { ((($velocity_0)**2 +($velocity_1)**2)/2.)**.5 }]
set bisection_time_c [ expr { $base_line * ( $velocity_0 - $bisection_velocity_c ) / ( $velocity_0 - $velocity_1 ) }]
set side5 $bisection_velocity_c
set side6 $bisection_1
set side7 $bisection_time_c
set side8 $calculation_1
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
console show;
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Babylonian Astronomy Trapezoid V2 Report , screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts "%|table $testcase_number|printed in| tcl format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |&"
puts "&| $side1 :|side height1 , degrees per day: | |&"
puts "&| $side2 :|side height2 , degrees per day: | |& "
puts "&| $side3 :|base line length1, days: | |& "
puts "&| $side4 :|base line length2, days: | |&"
puts "&| $side5 :|answers, bisection velocity_c degrees per day:| | |&"
puts "&| $side6 :|bisection, half area displacement degrees:| | |&"
puts "&| $side7 :|bisection_time_c days:| | |&"
puts "&| $side8 :|area displacement degrees:| | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 0.2 0.1583 0. 60. 0.1803 5.3745 28.2601 10.75 }
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 0.1583 0.0250 60. 120. 5.5 2.74949 20.2450 5.5 }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 0.2 0.0250 0. 120. 0.1425 3.375 39.4135 6.75 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .self_help -text self_help -command {self_help}
::ttk::button .console2 -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .console2 .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Babylonian Astronomy Trapezoid Area V2"
# gold on TCL Club, 8Jul2020
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK 8.6 license terms.
# Editorial rights retained under the TCL/TK license terms
# and will be defended as necessary in court.
# end of filePushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
Console program under test.
Expansion subroutine
gold - 2020-07-5
# console program written on Windows 10
# working under TCL version 8.6
# gold moniker on TCL WIKI , 7jul2020
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
proc expansion_procedure_2 { side1 side2 side3 side4 side5 epsilon } {
set counter 1
set token1 $side1
set token2 $side2
set token3 $side3
set epsilon [/ 1. $side5]
puts " %| Table of Natural Log and Round_off |% "
puts " %| counter | value | rounded value | ln | round off | round off |% "
while { $counter < 30. } {
#if { [abs [- $side4 [* $token1 $token2 $token3 1. ] ] ] < $epsilon } {break;}
#if { [- $side4 [* $token1 $token2 $token3 1. ] ] > 0 } {set correction_fraction [* 1. [/ 1. $side5] ]}
#if { [- $side4 [* $token1 $token2 $token3 1. ] ] < 0 } {set correction_fraction [* -1. [/ 1. $side5] ]}
#set correction_fraction [- $side3 [* $token1 $token2 1. ] ]
incr counter
set token1 [ expr ($token1 + .1 ) ]
set token2 [ expr (log ($token1)) ]
set round_off [format %7.2f $token2 ]
set value_rounded [format %7.2f $token1 ]
puts " &| $counter | $token1 | $value_rounded | $token2 | $round_off | $round_off |& "
} }
set side8 [ expansion_procedure_2 1.0 1.0 1.0 1000. 10. 1. ]
# printoutprintout
# pretty print from autoindent and ased editor
# Babylonian Expansion Procedure Algorithm Calculator V2
# console program written on Windows 10
# working under TCL version 8.6
# TCL WIKI , 2jul2020
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
proc expansion_procedure2 { side1 side2 side3 side4 side5 epsilon } {
set counter 1
set token1 $side1
set token2 $side2
set token3 $side3
set saver1 .00001
set saver2 .00001
set saver3 .00001
set epsilon [/ 1. $side5]
while { $counter < 1000. } {
if { [abs [- $side4 [* $token1 $token2 $token3 1. ] ] ] < $epsilon } {break;}
if { [- $side4 [* $token1 $token2 $token3 1. ] ] > 0 } {set correction_fraction [* 1. [/ 1. $side5] ]}
if { [- $side4 [* $token1 $token2 $token3 1. ] ] < 0 } {set correction_fraction [* -1. [/ 1. $side5] ]}
#set correction_fraction [- $side3 [* $token1 $token2 1. ] ]
set token1 [+ $token1 $correction_fraction ]
set token2 [+ $token2 $correction_fraction ]
set token3 [+ $token3 $correction_fraction ]
incr counter
puts " &| token1 | $token1 | token2 | $token2 | token3 | $token3 | product | [* $token1 $token2 $token3 ] | correction | $correction_fraction |& "
} }
set side8 [ expansion_procedure_2 9.6 9.6 9.6 1000. 60. .15 ]
# printout followsTable of Natural Log and Round_off
| Table of Natural Log and Round_off | |||||
|---|---|---|---|---|---|
| table | printed in | tcl wiki format | |||
| quantity | value | comment, if any | |||
| quantity | value | comment, if any | |||
| counter | value | rounded value | ln | round off | round off |
| 2 | 1.1000000000000001 | 1.10 | 0.095310179804324935 | 0.10 | 0.10 |
| 3 | 1.2000000000000002 | 1.20 | 0.18232155679395479 | 0.18 | 0.18 |
| 4 | 1.3000000000000003 | 1.30 | 0.26236426446749128 | 0.26 | 0.26 |
| 5 | 1.4000000000000004 | 1.40 | 0.33647223662121317 | 0.34 | 0.34 |
| 6 | 1.5000000000000004 | 1.50 | 0.40546510810816466 | 0.41 | 0.41 |
| 7 | 1.6000000000000005 | 1.60 | 0.47000362924573591 | 0.47 | 0.47 |
| 8 | 1.7000000000000006 | 1.70 | 0.53062825106217071 | 0.53 | 0.53 |
| 9 | 1.8000000000000007 | 1.80 | 0.58778666490211939 | 0.59 | 0.59 |
| 10 | 1.9000000000000008 | 1.90 | 0.64185388617239525 | 0.64 | 0.64 |
| 11 | 2.0000000000000009 | 2.00 | 0.69314718055994573 | 0.69 | 0.69 |
| 12 | 2.100000000000001 | 2.10 | 0.74193734472937778 | 0.74 | 0.74 |
| 13 | 2.2000000000000011 | 2.20 | 0.78845736036427061 | 0.79 | 0.79 |
| 14 | 2.3000000000000012 | 2.30 | 0.83290912293510455 | 0.83 | 0.83 |
| 15 | 2.4000000000000012 | 2.40 | 0.87546873735390041 | 0.88 | 0.88 |
| 16 | 2.5000000000000013 | 2.50 | 0.91629073187415555 | 0.92 | 0.92 |
| 17 | 2.6000000000000014 | 2.60 | 0.9555114450274369 | 0.96 | 0.96 |
| 18 | 2.7000000000000015 | 2.70 | 0.993251773010284 | 0.99 | 0.99 |
| 19 | 2.8000000000000016 | 2.80 | 1.0296194171811588 | 1.03 | 1.03 |
| 20 | 2.9000000000000017 | 2.90 | 1.0647107369924289 | 1.06 | 1.06 |
| 21 | 3.0000000000000018 | 3.00 | 1.0986122886681102 | 1.10 | 1.10 |
| 22 | 3.1000000000000019 | 3.10 | 1.1314021114911013 | 1.13 | 1.13 |
| 23 | 3.200000000000002 | 3.20 | 1.1631508098056815 | 1.16 | 1.16 |
| 24 | 3.300000000000002 | 3.30 | 1.1939224684724352 | 1.19 | 1.19 |
| 25 | 3.4000000000000021 | 3.40 | 1.2237754316221163 | 1.22 | 1.22 |
| 26 | 3.5000000000000022 | 3.50 | 1.2527629684953687 | 1.25 | 1.25 |
| 27 | 3.6000000000000023 | 3.60 | 1.2809338454620649 | 1.28 | 1.28 |
| 28 | 3.7000000000000024 | 3.70 | 1.3083328196501793 | 1.31 | 1.31 |
| 29 | 3.8000000000000025 | 3.80 | 1.3350010667323406 | 1.34 | 1.34 |
| 30 | 3.9000000000000026 | 3.90 | 1.3609765531356015 | 1.36 | 1.36 |
gold This page is copyrighted under the TCL/TK license terms, this license .
Comments Section
Please place any comments here, Thanks.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |