Polygon intersection
Richard Suchenwirth 2004-07-22 - Given the coordinates of two convex polygons (in the same meaning as canvas items), I wanted to determine the coordinates of the polygon where the two overlap. You can interpret this also as the intersection, if the two polygons represent sets of points inside them.
The idea was: The overlap polygon is bounded by the convex hull of those points where
- a side of one polygon crosses a side of the other, or
- a corner of one polygon is enclosed in the other
Enclosure of a point in a polygon was tested by checking whether the line between the point and another that is known to be inside the polygon (namely, its center :) crosses no boundaries of the polygon. So both criteria could be simplified down to checking whether, and if so, where, two lines cross.
And here's the code (make sure the functions ccw and hull2d from Convex hull are also available):
namespace eval polygon {}
proc polygon::overlap {p1 p2} {
set res {}
set lines2 [sides $p2]
#-- collect crossing points
foreach a [sides $p1] {
foreach b $lines2 {
set point [lines'cross $a $b]
if {$point ne ""} {lappend res $point}
}
}
#-- collects points of one polygon enclosed in the other
foreach a [corners $p1] {
if [enclosed $p2 $a] {lappend res $a}
}
foreach a [corners $p2] {
if [enclosed $p1 $a] {lappend res $a}
}
join [hull2d $res]
}
proc polygon::center coords {
# returns the x y coordinates of the center
set xsum 0.0
set ysum 0.0
set n 0
foreach {x y} $coords {
+= xsum $x
+= ysum $y
incr n
}
list [expr {$xsum/$n}] [expr {$ysum/$n}]
}
proc polygon::enclosed {coords point} {
set testline [concat $point [center $coords]]
foreach side [sides $coords] {
if {[lines'cross $side $testline] ne ""} {return 0}
}
return 1
}
proc polygon::sides coords {
foreach {x0 y0} $coords break
set res {}
foreach {x y} [lrange $coords 2 end] {
lappend res [list $x0 $y0 $x $y]
set x0 $x
set y0 $y
}
lappend res [list $x $y [lindex $coords 0] [lindex $coords 1]]
}
proc polygon::corners coords {
set res {}
foreach {x y} $coords {
lappend res [list $x $y]
}
set res
}
# This took me most thinking - find out whether (and where) two lines cross
# Let the point of intersection of the two lines be (x,y)
# 2x = xa * (1-p) + xb * (1+p) = xc * (1-q) + xd * (1+q)
# 2y = ya * (1-p) + yb * (1+p) = yc * (1-q) + yd * (1+q)
# The point of intersection lies within the first line segment
# if and only if p<=1, and within the second line segment
# if and only if q<=1. We recast this into a 2x2 linear
# system and solve. We avoid dividing by the determinant
# until we've determined that both intersections lie within
# the lines in question
proc lines'cross { line1 line2 } {
foreach { xa ya xb yb } $line1 break
foreach { xc yc xd yd } $line2 break
set det [expr { ( $xb - $xa ) * ( $yd - $yc )
- ( $xd - $xc ) * ( $yb - $ya ) }]
if { $det == 0 } { # line segments are parallel
# or collinear
return {}
}
set nump [expr { ( $xd - $xc ) * ( $yb + $ya )
- ( $xb + $xa ) * ( $yd - $yc )
+ 2. * ( $xc * $yd - $xd * $yc ) }]
if { abs($nump) > abs($det) } { # point of intersection is
# outside first line segment
return
}
set numq [expr { ( $xd + $xc ) * ( $yb - $ya )
- ( $xb - $xa ) * ( $yd + $yc )
+ 2. * ( $xb * $ya - $xa * $yb ) }]
if { abs($numq) > abs($det) } { # point of intersction is
# outside second line segment
return
}
set p [expr { $nump / $det }]
set opp [expr { 1. + $p }]
set omp [expr { 1. - $p }]
set x [expr { ($xa * $omp + $xb * $opp) / 2. }]
set y [expr { ($ya * $omp + $yb * $opp) / 2. }]
return [list $x $y]
}KBK - Another approach to intersection of polygons, due to Sutherland and Hodgman, is common in graphics applications, where it is used to clip polygons to the screen borders. Normally, it's pretty ugly, but Tcl 8.6 and coroutines make it fairly straightforward.
# cw --
#
# Does the path (x0,y0)->(x1,y1)->(x2,y2) turn clockwise
# or counterclockwise?
#
# Parameters:
# x0, y0 - First point
# x1, y1 - Second point
# x2, y2 - Third point
#
# Results:
# Returns 1 if point 2 is to the right of a line joining points 0
# and 1, and -1 if it is to the left of the line.
#
# If the three points are collinear, returns 1 if the third point is
# the middle point, -1 if point 0 is the middle point, 0 if
# point 1 is the middle point
proc cw {x0 y0 x1 y1 x2 y2} {
set dx1 [expr {$x1 - $x0}]; set dy1 [expr {$y1 - $y0}]
set dx2 [expr {$x2 - $x0}]; set dy2 [expr {$y2 - $y0}]
# (0,0,$dx1*$dy2 - $dx2*$dy1) is the crossproduct of
# ($x1-$x0,$y1-$y0,0) and ($x2-$x0,$y2-$y0,0).
# Its z-component is positive if the turn
# is clockwise, negative if the turn is counterclockwise.
set pr1 [expr {$dx1 * $dy2}]
set pr2 [expr {$dx2 * $dy1}]
if {$pr1 > $pr2} {
# Clockwise
return 1
} elseif {$pr1 < $pr2} {
# Counter-clockwise
return -1
} elseif {$dx1*$dx2 < 0 || $dy1*$dy2 < 0} {
# point 0 is the middle point
return 0
} elseif {($dx1*$dx1 + $dy1*$dy1) < ($dx2*$dx2 + $dy2+$dy2)} {
# point 1 is the middle point
return 0
} else {
# point 2 lies on the segment joining points 0 and 1
return 1
}
}
# intersect --
#
# Calculate the point of intersection of two lines
# containing the line segments (x1,y1)-(x2,y2) and (x3,y3)-(x4,y4)
#
# Parameters:
# x1,y1 x2,y2 - Endpoints of the first line segment
# x3,y3 x4,y4 - Endpoints of the second line segment
#
# Results:
# Returns a two-element list containing the point of intersection.
# Returns an empty list if the line segments are parallel
# (including the case where the segments are concurrent).
proc intersect {x1 y1 x2 y2 x3 y3 x4 y4} {
set d [expr {($y4 - $y3) * ($x2 - $x1)
- ($x4 - $x3) * ($y2 - $y1)}]
set na [expr {($x4 - $x3) * ($y1 - $y3)
- ($y4 - $y3) * ($x1 - $x3)}]
if {$d == 0} {
return {}
}
set r [list \
[expr {$x1 + $na * ($x2 - $x1) / $d}] \
[expr {$y1 + $na * ($y2 - $y1) / $d}]]
return $r
}
# pairs --
#
# Coroutine that yields the elements of a list in pairs
#
# Parameters:
# list - List to decompose
#
# Immediate result:
# Returns the name of the coroutine
#
# Further results:
# Returns two-element ranges from the given list, one at a time.
# Returns {} at the end of the iteration.
proc pairs {list} {
yield [info coroutine]
foreach {x y} $list {
yield [list $x $y]
}
return {}
}
# clipsegment --
#
# Clips one segment of a polygon against a line.
#
# Parameters:
# inside0 - Flag = 1 if sx0,sy0 is to the right of the clipping line
# cx0,cy1 cx1,cy1 - Two points determining the clipping line
# sx0,sy0 sx1,sy1 - Two points determining the subject line
#
# Results:
# Returns 1 if sx1,sy1 is to the right of the clipping line, 0 otherwise
#
# Yields:
# Yields, in order:
#
# The intersection point of the segment and the line, if
# the segment intersects the line.
#
# The endpoint of the segment, if the segment ends to the
# right of the line.
proc clipsegment {inside0 cx0 cy0 cx1 cy1 sx0 sy0 sx1 sy1} {
set inside1 [expr {[cw $cx0 $cy0 $cx1 $cy1 $sx1 $sy1] > 0}]
if {$inside1} {
if {!$inside0} {
set int [intersect $cx0 $cy0 $cx1 $cy1 \
$sx0 $sy0 $sx1 $sy1]
if {[llength $int] > 0} {
yield $int
}
}
yield [list $sx1 $sy1]
} else {
if {$inside0} {
set int [intersect $cx0 $cy0 $cx1 $cy1 \
$sx0 $sy0 $sx1 $sy1]
if {[llength $int] > 0} {
yield $int
}
}
}
return $inside1
}
# clipstep --
#
# Coroutine to perform one step of Sutherland-Hodgman polygon clipping
#
# Parameters:
# source - Name of a coroutine that will return the vertices of a
# subject polygon to clip, and return {} at the end of the
# iteration.
# cx0,cy0 cx1,cy1 - Endpoints of an edge of the clip polygon
#
# Immediate result:
# Returns the name of the coroutine
#
# Further results:
# Returns the vertices of the clipped polygon
proc clipstep {source cx0 cy0 cx1 cy1} {
yield [info coroutine]
set pt0 [{*}$source]
if {[llength $pt0] == 0} {
return
}
lassign $pt0 sx0 sy0
set inside0 [expr {[cw $cx0 $cy0 $cx1 $cy1 $sx0 $sy0] > 0}]
set finished 0
while {!$finished} {
set thispt [{*}$source]
if {[llength $thispt] == 0} {
set thispt $pt0
set finished 1
}
lassign $thispt sx1 sy1
set inside0 [clipsegment $inside0 \
$cx0 $cy0 $cx1 $cy1 $sx0 $sy0 $sx1 $sy1]
set sx0 $sx1
set sy0 $sy1
}
return {}
}
# clippoly --
#
# Perform Sutherland-Hodgman polygon clipping
#
# Parameters:
# cpoly - Coordinates of the clip polygon, listed in clockwise order.
# spoly - Coordinates of the subject polygon, listed in clockwise order.
#
# Results:
# Returns the coordinates of the clipped polygon, listed in clockwise
# order.
#
# The clip polygon must be convex. The subject polygon may be any polygon,
# including degenerate and self-intersecting ones.
# The procedure works by composing coroutines that clip the subject polygon
# against each edge of the clip polygon in sequence.
proc clippoly {cpoly spoly} {
variable clipindx
set source [coroutine clipper[incr clipindx] \
pairs $spoly]
set cx0 [lindex $cpoly end-1]
set cy0 [lindex $cpoly end]
foreach {cx1 cy1} $cpoly {
set source [coroutine clipper[incr clipindx] \
clipstep $source $cx0 $cy0 $cx1 $cy1]
set cx0 $cx1; set cy0 $cy1
}
set result {}
while {[llength [set pt [{*}$source]]] > 0} {
lappend result {*}$pt
}
return $result
}
# DEMONSTRATION PROGRAM
if {![info exists ::argv0] || [string compare $::argv0 [info script]]} {
return
}
package require Tk
grid [canvas .c -width 800 -height 400 -background \#ffffff]
proc demonstrate {cpoly spoly} {
.c create polygon {*}$cpoly -outline \#ff0000 -fill {} \
-width 5
.c create polygon {*}$spoly -outline \#0000cc -fill {}
.c lower [.c create polygon {*}[clippoly $cpoly $spoly] \
-fill \#ffff99 -outline {}]
}
demonstrate {100 100 300 100 300 300 100 300} \
{50 100 350 100 350 300 250 300 200 250 150 350 100 250 100 200}
demonstrate {600 100 700 100 725 200 700 300 600 300 575 200} \
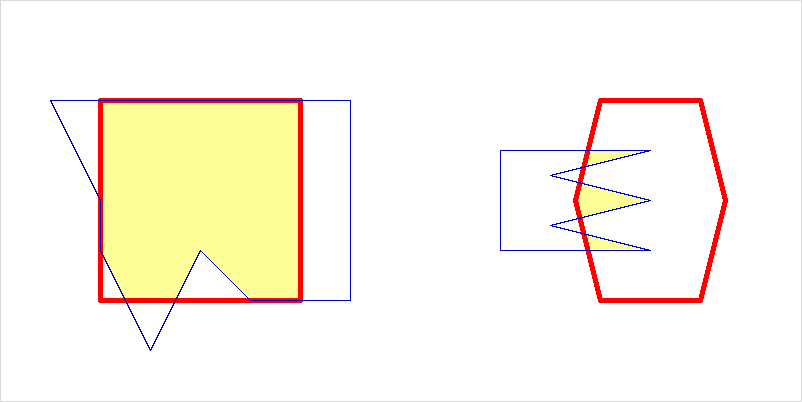
{500 150 650 150 550 175 650 200 550 225 650 250 500 250}The demonstration shows some of the peculiarities of the algorithm. The left-hand image shows a subject polygon being clipped against a rectangle. The right-hand image shows how non-convex subject polygons can give rise to degenerate result polygons, where edges are coincident. (There are other algorithms, like Weiler-Atherton, that can return lists of polygons for this case.
In the important case where both subject and clip polygons are convex, there are also better algorithms than what is presented here.
Arts and crafts of Tcl-Tk programming