Stick Shadow Time From VEDIC Math Astronomy & demo example TCL calculator, numerical analysis
Stick Shadow Time From VEDIC Math Astronomy & demo example TCL calculator, numerical analysis
This page is under development. Constructive comments are welcome, but please load any constructive comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 08Jul2020
- Stick Shadow Time From VEDIC Math Astronomy & demo example TCL calculator, numerical analysis
- Calculator Use
- Pseudocode Section
- More References from Stack B.
- Appendix Code
- Console program under test.
- printout
- Table of Natural Log and Round_off
- Comments Section
Preface
gold Here are some TCL calculations for Stick Shadow Time From VEDIC Math Astronomy. The Vedic formula for Stick Shadow Time was loaded into a TCL calculator gui. Additional console program below is used to check or improve subroutine.
Introduction
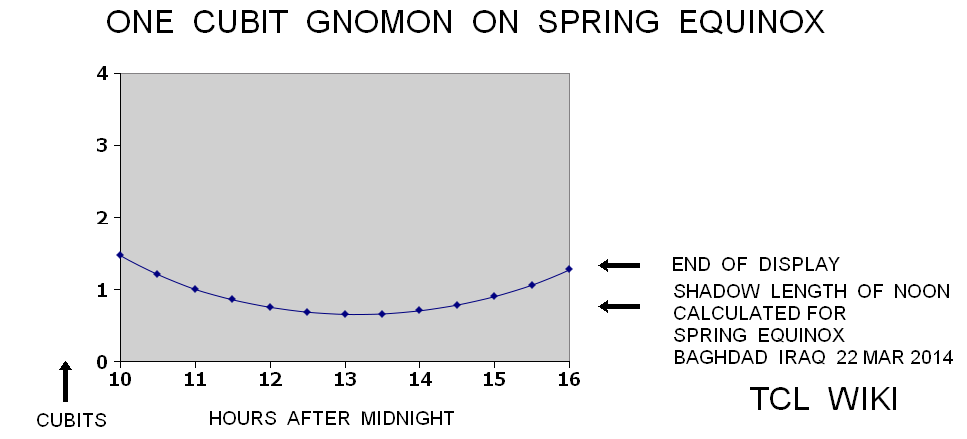
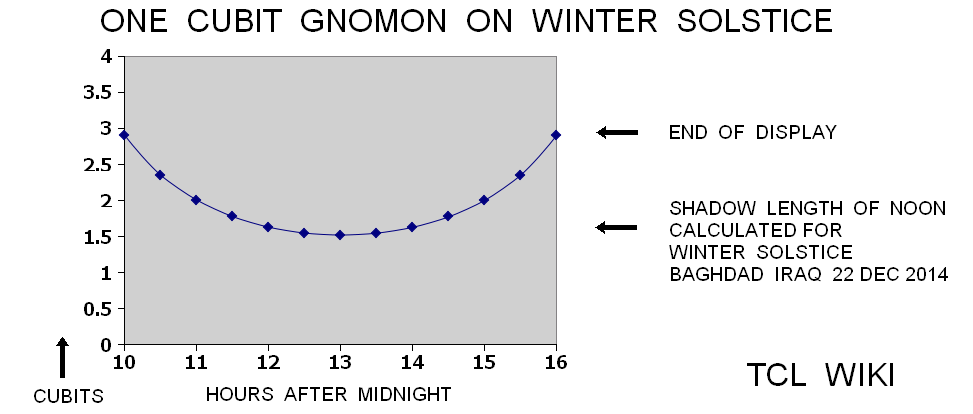
The Vedic formula is the ratio of day over 2*time, d/(2*t) = ((S-S0)/g)+C , where S is horizontal shadow length, time is length of day, S0 is shadow length at noon, d is time of day as relative portion of 24 hours. The vertical sun stick or gnomon length <g> is usually a constant length over the sessions. The constant C is usually one, but may change as a function of latitude depending on the location of measurements. The Vedic formula is measuring the ratios of gnomon and shadow length, so the units cancel out. Mostly, the stick shadow equals length of the vertical stick gnomon at the time of high noon on equator. For restating the problem in a computer algorithm, the calculator will be in conventional modern units.
The Vedic math is primarily studied for historical purposes. The earliest Babylonian and Vedic examples of stick shadows did not use algebra notation, decimal notation, sin/cos trigonometry, or modern units, so the reader will have to bear some anachronisms in the TCL code. At least one approach for the modern reader and using modern terminology is to develop the implied algebraic equations and decimal equivalents from the text translations. Then the TCL calculator can be run over a number of testcases to validate the algebraic equations. For the examples of presenting algorithms to modern readers, the calculator shell will give results in modern decimal units. The units can be changed in the internal calculator formulas as TCL code. Any convenient and consistent output units might be used like millimeters, inches, cubits, feet, or dollars to donuts.
Procedures
For comparison of the Vedic and Babylonian algorithm(s) with conventional Western methods, the TCL code may include redundant procedures, redundant calculation paths, and printout check formulas to compute product, area, check diagnostics, and relative errors.
Testcases are important in development of TCL programs.
In planning any software, it is advisable to gather a number of testcases to check the results of the program. Here, a TCL slot calculator is being used as a testbed for the Vedic gnomon shadow ratios. The results of the testcases are estimated using the hand calculator and then checked in the slot calculator. Pseudocode and equations are developed from the hand calculations and theory. Small console programs are written to check or proof the alternate subroutines or procedures, rather than keeping the unblessed code and comment lines in the main slot calculator. Finally the improved or alternate subroutines are loaded into the slot calculator. The TCL slot calculator is effectively a shell program to input entries, retain loaded standard testcases, host calculation routines, and display results. Additional significant figures are used to check the TCL calculator, not to infer the accuracy of inputs and product reports. Four significant figures is considered sufficient for most engineering projects.
Most of the testcases involve experiments or models, using assumptions, and rules of thumb. For the push buttons in the TCL calculator, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console to conventional texteditor. For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers should be cleared either on the clear button or on the next solve button.
Discussion
The extant portions of the cited Astronomy procedure texts are usually very terse, spotty, and need a lot of backgound for understanding.
The hand techniques that the Babylonian Astronomers used to measure sky angles are not well known to the later amateurs. However, the Babylonian Astronomy diaries record the angular measurements of stars in cubits and susi. In some older tablet translations, susi are translated fingers. There are either 20 or 24 susi in a cubit depending on the era of the tablet. The clay tablets also record some calculations using the Us Babylonian unit or 4 minutes of time. An Us or one unit of the water clock is equivalent to one modern degree of angle. One cubit in the sky for celestial angles is equivalent to 2 Us or 2 degrees. Using proportions, a Babylonian susi or finger might be about (1 cubit)/(24 susi)*(2 degrees) / (1 cubit) or < expr (1./24.)*(2./1. > or 0.083 degree. 6 fingers would be < expr (1./24.)*(2./1. )*6.> or 0.5 degrees.
One possible hand technique to measure sky angles is to hold a straight edge or ruler at arms length and parallel to the to the heavens. For the modern observer, the sun or moon is convenient standard of 5 degrees across the disc. For example on a given night, if a star is observed 4 lunar discs from the moon, then the equivalent angle would be < expr 4*5. > or 20 degrees. If one takes a blank wooden ruler of about 1 foot and marks the apparent lunar disc in successions across the ruler, that ruler might give some rough measure of sky angles. With a little patience and dodging summer mosquitoes, one can further divide one or two of the successive lunar markings into fifths for a degree mark. Both the ancient Babylonian and Egyptians had both hand rulers and measuring rods marked in cubits, so this possible hand technique seems likely. Actually with a little experience, a single human finger width at arms reach is about 1 degree. Or combined finger joints of an out stretched hand against the sky can give a rough angle measurement.
In the Babylonian Astronomy instruction texts, the Babylonian mathematicians appear to be solving the problem of sun stick time by graphical methods. Unfortunately, a lot of the context, turns of phrase, and off tablet calculations has been lost to modern readers of the Babylonian Astronomy instruction texts. The rarity of the Babylonian Astronomy instruction texts means that sometimes there is not a full understanding of the word usage to the linguists. The Vedic or later Sanskrit results on stick shadows use more understandable arithmetic and context to modern readers, aside from the wealth of Sanskrit literature for linguist comparison.
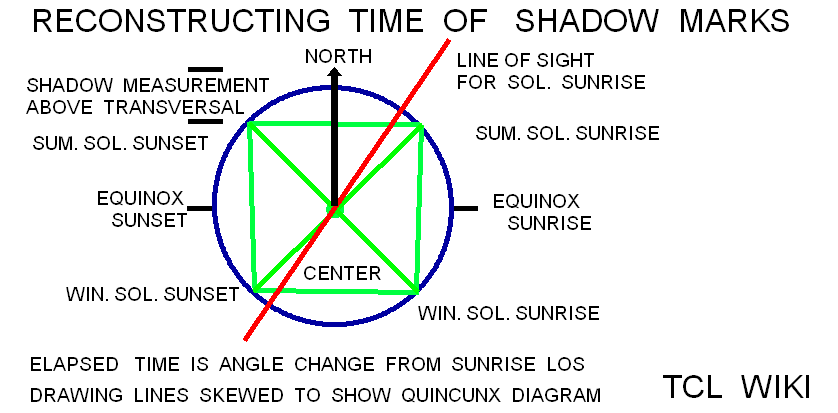
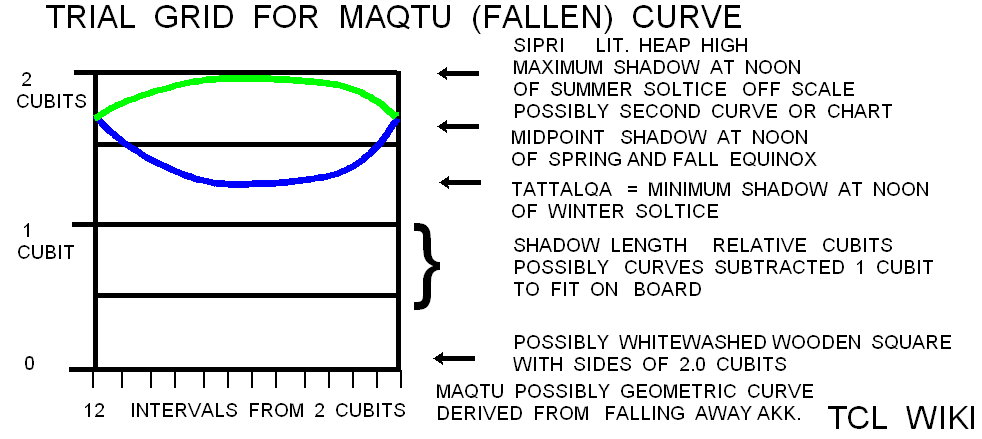
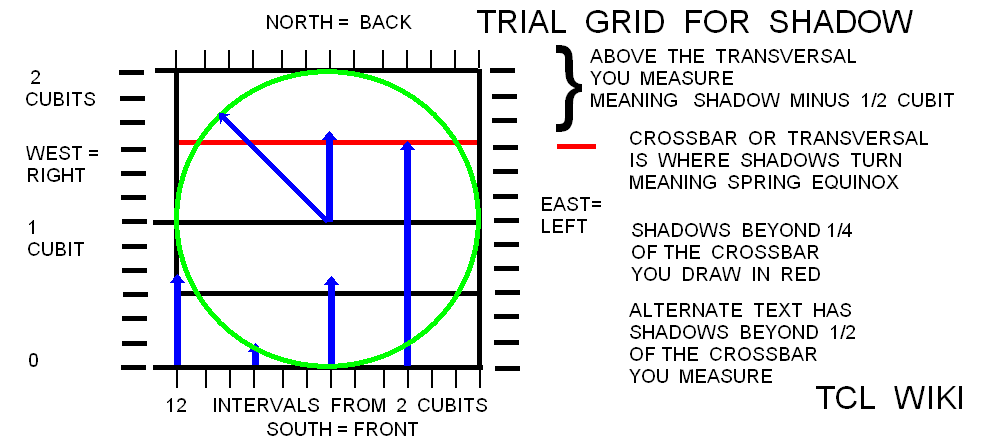
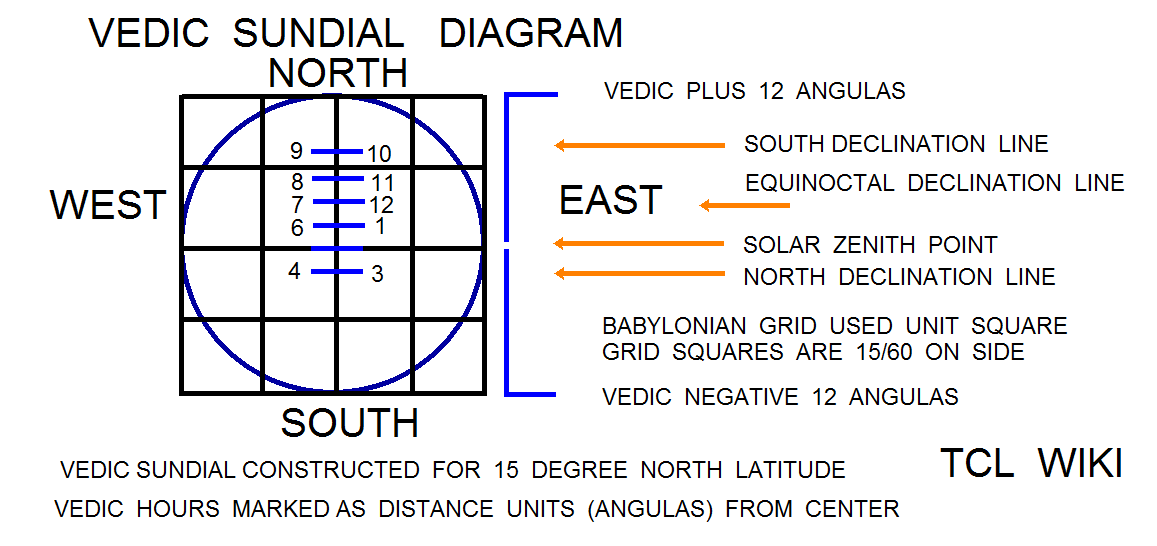
The research is looking for hints on the gnomon and the horizontal diagram or dial discussed in the Hindu astronomy and Surya Siddhanta. In Early Indian Astronomy by George Abraham, the term (shadow minus noon shadow) is used in a Hindu formula for daylight length as d/(2*t)=( (S-S0)/g )+1, where g is gnomon length, S is shadow length,S0 is shadow length at noon, and t/d is fraction of time from sunrise over the total daylight time. In the Indian Sanskrit literature, the shadow on the horizontal dial is called the bhuj or earth and forms a right triangle with the upright gnomon (nara yantra (man instrument) or sandu (stake)). The hypotenuse would be from the upper tip of the gnomon to the end of the shadow. The angle on the horizontal chart between North and the shadow is the azimuth of the sun from North, referring to the Babylonian gnomon alignment in the Northern hemisphere. The angle on the horizontal dial between the East to West line and the shadow on the dial is translated as "amplitude of the sun" (agra). The total shadow or parts of the shadow (subtracting the equinox shadow, antya) are translated as the rsine (radius*sine) of the solar amplitude (agra jya). Agra is derived from a root word meaning field.
gold 10/24/2020. There may be some inconsistencies in the table definitions. To get <d/2t=2> at noon, one would have to use a 24 hour day as proof follows. If d/t is fraction of time for 24 hours of total day and night over time from sunrise. d/2t is fraction of time for total and night time over 2X time from sunrise. Reconstructing for the ideal case of noon at the equator, then day length equals night length at equinox. At noon in Western hour assumptions, t/d equals 6/24 or 1/4, d/t equals 24/6 or 4, and d/2t equals 24/(2*6) or 2. For the ideal case as understood here, midmorning would be 3 hours before noon or 3 hours after sunrise. At midmorning, t/d equals 3/24 or 1/8, d/t equals 24/3 or 8, and d/2t equals 24/(2*3) or 4. Refer to Table 1, Time Estimate Vedic Math.
The factors 1/4 and 1/2 have been seen before in Babylonian time of shadow calculations. In Shadow-Length Schemes by Dr. Steele, 1/4 and 1/2 were factors used to calculate daily changes in the time after sunrise to the midmorning shadow and noon shadow of the gnomons. The Babylonians measured these changes in "us" units (4 minutes each on a water clock) . In a simplified form, the first equation would be daily change in daylight period in "us" units times 1/4 equals daily change in time from sunrise to midmorning. The second equation would be daily change in daylight period in us units times 1/2 equals daily change in time from sunrise to noon. Not sure about the validity in astronomy, but the measurement system in the texts transfers proportions in time (from the Mul Apin) to proportions in gnomon shadow length. The shadow function(1/4) equals daily shadow change at midmorning (1 cubit shadow) and shadow function(1/2) equals daily shadow change at noon. The functions for time after sunrise and shadow length are attempting to model nonlinear quantities with a constant rate or proportions. In terms of the math available to the Babylonians, a long table for every day or month of the year would probably be more effective.
Calculator Use
For the TCL calculator, the length of any gnomon is normalized or set in the master length as 100 units or 100 centimeters. The vertical stick length or gnomon length is usually constant over the session. The units cancel out in the formula. The gnomon master length could be in inches or feet with the same units returned on the shadow.
Conclusions
The TCL calculator is replicating correctly the gnomon shadow table in the Abrahams paper.
Table 1, Time Estimate Vedic Math
| Table 1 | Time Estimate Vedic Math | printed in | tcl format | |
|---|---|---|---|---|
| 1: | testcase_number | |||
| quantity | value | value | value | comment, if any |
| Western assumptions | d/2t Vedic Time | s/g | t/d | |
| 0800 AM | 9 | 8 | 1/18 | early morning |
| 0900 AM | 7 | 6 | 1/14 | |
| 1000 AM | 4 | 4 | 1/8 | mid morning |
| 1100 AM | 3 | 2 | 1/6 | |
| 1200 AM | 2 | 1 | 1/4 | mostly equal gnomon and shadow at equator & equinox |
| 1300 PM | 5/3 | 2/3 | 3/10 | |
| 1400 PM | 4/3 | 1/3 | 3/8 | mid afternoon |
| 1500 PM | 1 | 0 | 1/2 | late afternoon |
Based on table in Early Indian Astronomy by George Abraham. The Bablylonians and Vedics probably used quarterday watches with two hour increments, but not sure how Vedics called out their hours. A watch is expr 24./4. or 6 hours long. There would be expr 6./2. or 3 segments of two hours in a watch. Reconstructing for the ideal case of noon at the equator, then day length equals night length at spring and fall equinox.
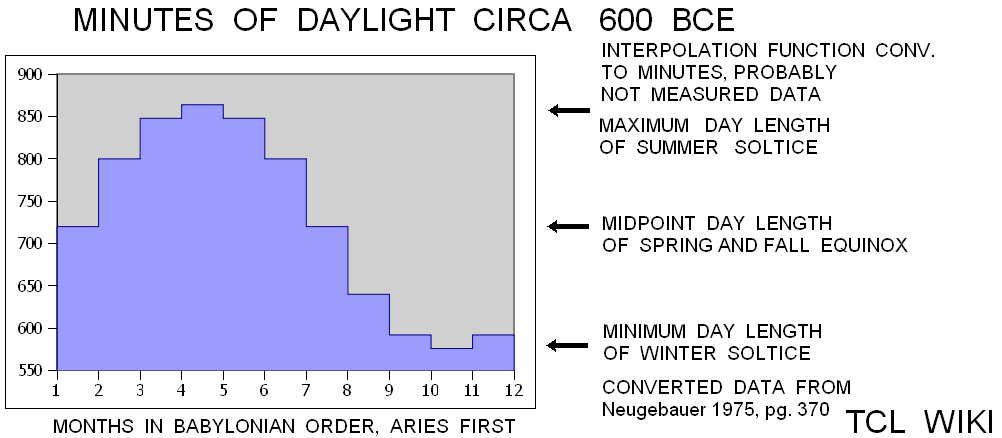
Table 2,Babylonian Day Length Circa 600 BCE
| Month | Constellation | minutes | decimal minas |
|---|---|---|---|
| 1 | Aries | 720 | 3 |
| 2 | Taurus | 800 | 3.3 |
| 3 | Gemini | 848 | 3.53 |
| 4 | Cancer | 864 | 3.6 |
| 5 | Leo | 848 | 3.53 |
| 6 | Virgo | 800 | 3.33 |
| 7 | Libra | 720 | 3 |
| 8 | Scorpius | 640 | 2.66 |
| 9 | Sagittarius | 592 | 2.46 |
| 10 | Capricorn | 576 | 2.4 |
| 11 | Aquarius | 592 | 2.46 |
| 12 | Pisces | 640 | 2.66 |
| converted data from Neugebauer 1975, pg. 370) |
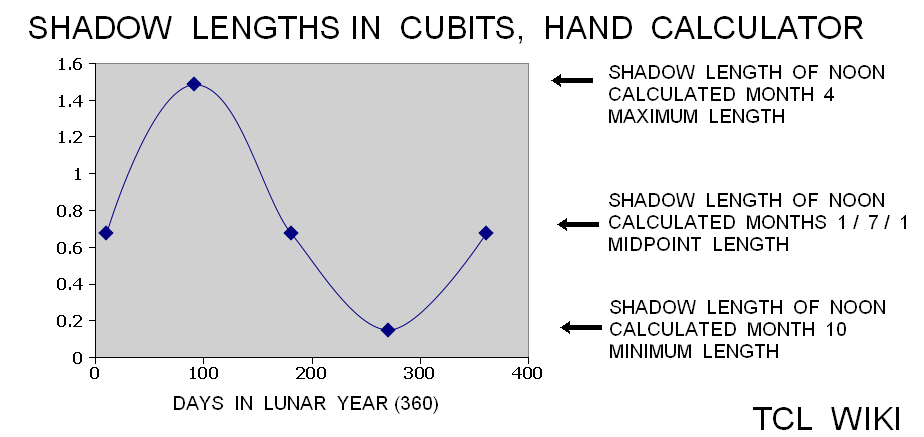
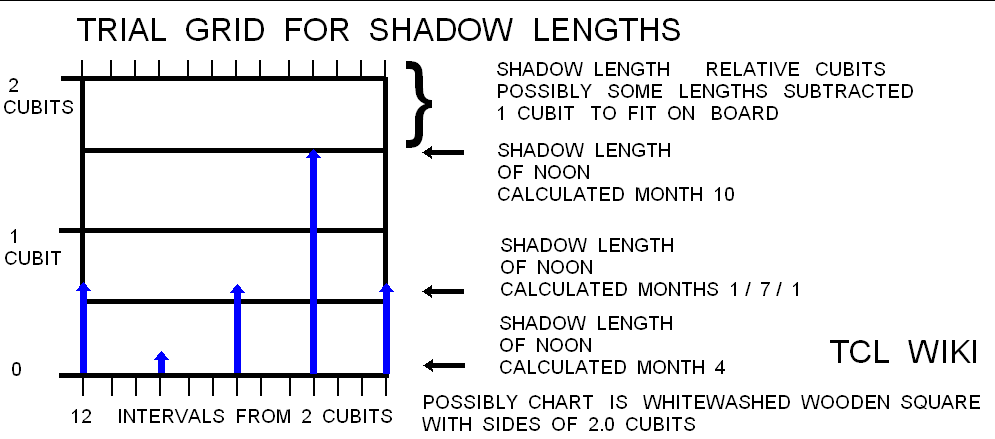
Table 3,Babylonian Noon Shadows, hand calculator
| hand calculator | formula | months in | Babylonian order | ||
|---|---|---|---|---|---|
| shadow length cubits | decimal cubits | days lunar year | B. month | constellation=month | comment |
| 38/60 | 0.6733 | 10 | 1 | Aries | spring equinox, midpoint shadow |
| 89/60 | 1.4833 | 91 | 4 | Cancer | summer solstice, maximum shadow |
| 38/60 | 0.6733 | 181 | 7 | Libra | fall equinox, midpoint shadow |
| 9/60 | 0.15 | 271 | 10 | Capricorn | winter solstice, minimum shadow |
| 38/60 | 0.6733 | 361 | 1 | Aries | spring equinox, midpoint shadow |
Table 4,Trial Reduction of he-gal or handuhhu, hand calculator
| B. month | he-gal, handuhhu | noon length (modern formula) | mid morning shadow? | possible reduction |
|---|---|---|---|---|
| B. month | cubits? | cubits | cubits | cubits |
| 4 | 60/60 | 89/60 | 60/60 | 89/60-(38/60)*.707=62/60 |
| 5 | 50/60 | 72/60 | 65/60 | 72/60-(38/60)*.707=45/60 |
| 6 | 40/60 | 60/60 | 70/60 | 60/60-(38/60)*.707=33/60 |
| 7 | 30/60 | 38/60 | 75/60 | 38/60-(38/60)*.707=11/60 |
| 8 | 20/60 | 36/60 | 80/60 | 36/60-(38/60)*.707=11/60 |
| 9 | 10/60 | 22/60 | 85/60 | minus number not used in B. |
| 10 | (5/60? ) | 9/60 | 90/60 | minus number not used in B. |
Pseudocode Section
# using pseudocode
# possible problem instances
initialize algorithm_result = 1.
check algorithm
check_sum = a+b+c+d+e = original
set answers and printout with resulting values
pseudocode: need test cases > small,medium, giant
pseudocode: need testcases within range of expected operation.
pseudocode: are there any cases too small or large to be solved?
more than one formula for 1) tables and 2) calculator shell
Babylonian multiplication rule a * b = ((a + b)/2)^2 - ((a - b)/2)^2 # used in calculator shell
conventional Western formula for quarter square multiplication tables
is a * b= (1/4)*(((a+b)**2) - ( (a-b)**2 ) ) # used in Western tables circa 1600 to 1950 CE.
quarter square multiplication formula for the tables
is x*y = <.25* (x+y)**2> * <.25* (x-y)**2>.
# recommended, avoids division by zero
half square multiplication formula for the tables
may be equivalent to x*y = 0.5* <.5* (x+y)**2> * <.5* (x-y)**2> # used in tables,
# recommended, avoids division by zero
modern extension to the Babylonian multiplication algorithm
from the binomial theorem is a*b = 0.5*{a+b)**2 -a**2-b**2} # considered for calculator shell
a * b = expr { $a * $b } # TCL math.c call for check answer
QS(N) = (1/4) * N**2 , or 0.25 * N**2, or int’ed [ int [ expr 0.25*$N**2]]
HS(N) = (1/2) * N**2 , or 0.5 * N**2, or int’ed [ int [ expr 0.5*$N**2 ]]
approximate Babylonian quadrilateral formula expr <((a+c)/2) *((b+d)/2) > (not exact!!!)
product of 50*40*30 using modern base_60 logarithms, # used in thinking pod
the sum of logs is expr { 0.95546+0.90096+0.830706} , 2.687126.
The antilog in base_60 is expr 60**2.687126= 59995.193.
For the tables, the int function is used to clip remainders to integers.
the precision function by [AM] is used occasionally, but not every time.
note: mental and undocumented components in the Babylonian multiplication methods.
# exponent/ logarithm expressions
log (sqrt (m)) = (1/2)*log (m)
log (crt (m)) = (1/3)*log (m)
log (sqrt (m)) = (1/2)*log (m)
(1/2) = log (sqrt (m)) / log (m)
(1/2) = log (sqrt (m)) - (m))
log (crt (m)) = (1/3)*log (m)
(1/3) = log (crt (m)) / log (m)
(1/3) = log (crt (m)) - (m))
(1/2) = log (sqrt (m)) / log (m)
(2/1) = log (m) / log (sqrt (m))
2 = log (m - (sqrt (m))
(3/1) = log (m) / log (crt (m))
3 = log (m - (crt (m))
N = log (m - (N’rt(m))
N+1 = log (m - ((N+1)’rt(m))
log2 defined as ln N / ln 2 ,
log2 N =~ 1.442695 * ln N
log2 N =~ 3.321928 * log10 N
proc pyra_d {hh bb} { [ acotand [* .5 [/ $bb $hh] ]] }
# seked = (7 * .5 * 360 cubits) / 250 cubits = 5.04 decimal palms
proc seked_d {hh bb} { [/ [* 7. .5 $bb ] $hh ] }
# usage seked 250. 360. equals 5.04
# end of file, pseudocode:Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
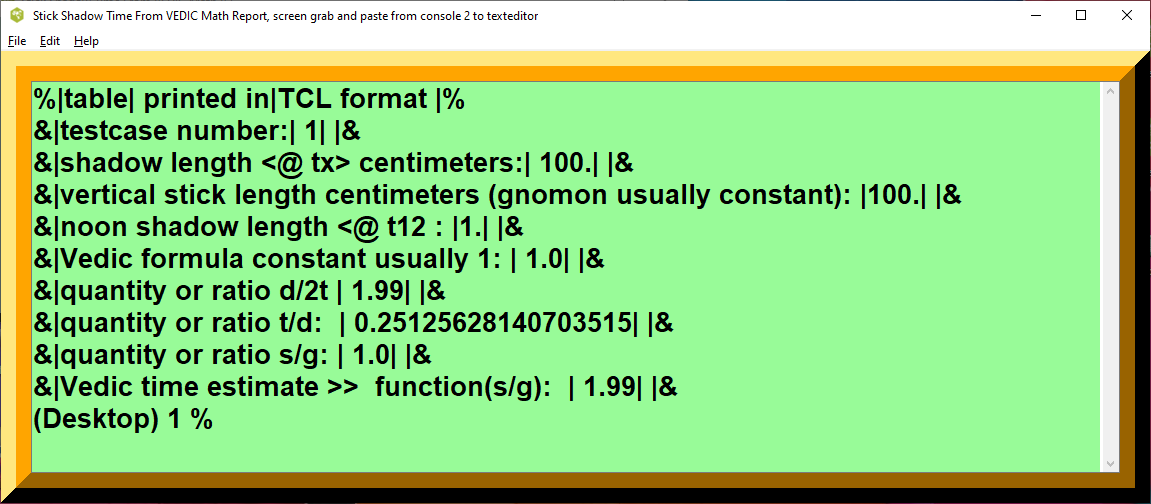
Testcase 1
| table | printed in | TCL format |
|---|---|---|
| testcase number: | 1 | |
| shadow length <@ tx> centimeters: | 100. | |
| vertical stick length centimeters (gnomon usually constant): | 100. | |
| noon shadow length <@ t12 : | 1. | |
| Vedic formula constant usually 1: | 1.0 | |
| quantity or ratio d/2t | 1.99 | |
| quantity or ratio t/d: | 0.25 | (1/4) integer fraction |
| quantity or ratio s/g: | 1.0 | (1/1) integer fraction |
| Vedic time estimate >> function(s/g): | 1.99 |
Testcase 2
| table | printed in | TCL format |
|---|---|---|
| testcase number: | 2 | |
| shadow length <@ tx> centimeters: | 33. | |
| vertical stick length centimeters (gnomon usually constant): | 100. | |
| noon shadow length <@ t12 : | 1. | |
| Vedic formula constant usually 1: | 1.0 | |
| quantity or ratio d/2t | 1.32 | |
| quantity or ratio t/d: | 0.38 | |
| quantity or ratio s/g: | 0.33 | (1/3) integer fraction |
| Vedic time estimate >> function(s/g): | 1.32 |
Testcase 3
| table | printed in | TCL format |
|---|---|---|
| testcase number: | 3 | |
| shadow length <@ tx> centimeters: | 66. | |
| vertical stick length centimeters (gnomon usually constant): | 100. | |
| noon shadow length <@ t12 : | 1. | |
| Vedic formula constant usually 1: | 1.0 | |
| quantity or ratio d/2t | 1.65 | |
| quantity or ratio t/d: | 0.303 | |
| quantity or ratio s/g: | 0.66 | (2/3) integer fraction |
| Vedic time estimate >> function(s/g): | 1.65 |
Testcase 4
| table | printed in | TCL format |
|---|---|---|
| testcase number: | 4 | |
| shadow length <@ tx> centimeters: | 800. | |
| vertical stick length centimeters (gnomon usually constant): | 100. | |
| noon shadow length <@ t12 : | 1. | |
| Vedic formula constant usually 1: | 1.0 | |
| quantity or ratio d/2t | 8.99 | |
| quantity or ratio t/d: | 0.055 | |
| quantity or ratio s/g: | 8.0 | (8/1) integer fraction |
| Vedic time estimate >> function(s/g): | 8.99 |
Testcase 5
| table | printed in | TCL format |
|---|---|---|
| testcase number: | 2 | |
| shadow length <@ tx> centimeters: | 600. | |
| vertical stick length centimeters (gnomon usually constant): | 100. | |
| noon shadow length <@ t12 : | 1. | |
| Vedic formula constant usually 1: | 1.0 | |
| quantity or ratio d/2t | 6.99 | |
| quantity or ratio t/d: | 0.07153075822603719 | |
| quantity or ratio s/g: | 6.0 | (6/1) integer fraction |
| Vedic time estimate >> function(s/g): | 6.99 |
Testcase 6
| table | printed in | TCL format |
|---|---|---|
| testcase number: | 6 | |
| shadow length <@ tx> centimeters: | 400. | |
| vertical stick length centimeters (gnomon usually constant): | 100. | |
| noon shadow length <@ t12 : | 1. | |
| Vedic formula constant usually 1: | 1.0 | |
| quantity or ratio d/2t | 4.99 | |
| quantity or ratio t/d: | 0.100 | (1/10) integer fraction |
| quantity or ratio s/g: | 4.0 | (4/1) integer fraction |
| Vedic time estimate >> function(s/g): | 4.99 |
Testcase 7
| table | printed in | TCL format |
|---|---|---|
| testcase number: | 7 | |
| shadow length <@ tx> centimeters: | 200. | |
| vertical stick length centimeters (gnomon usually constant): | 100. | |
| noon shadow length <@ t12 : | 1. | |
| Vedic formula constant usually 1: | 1.0 | |
| quantity or ratio d/2t | 2.99 | |
| quantity or ratio t/d: | 0.167 | |
| quantity or ratio s/g: | 2.0 | (2/1) integer fraction |
| Vedic time estimate >> function(s/g): | 2.99 |
Screenshots Section
figure 1a.
figure 1b.
figure 2.
figure 3.
figure 4.
figure 5.
figure 6.
figure 7.
figure 8.
figure 9.
figure 10.
figure 11., Test Sundial Hour Markers from IChing sticks
figure 12. Portable Solar Hour Dial from Ancient Egyptian Pattern
Note the hour markers are short distances and non-linear from the vertical stick gnomon. Canting the gnomon for a zero shadow length at noon is a possiblity.
Primary References:
- Babylonian Astronomy, LIS BRACK-BERNSEN AND JOHN M. STEELE†
- Celestial Measurement in Babylonian Astronomy J. M. Steele, 13 Jun 2007
- Lunar Eclipse Astronomy,Kristian Peder Moesgaard,August 2011
- Eclipse Predictions and Earth's Rotation[L1 ]
- Delta T (ΔT) and Universal Time[L2 ]
- Shadow-Length Schemes in Babylonian Astronomy,J. M. Steele, SCIAMVS 14 (2013), 3-39,revised 2012
- Brack-Bernsen, L. and Hunger, H., 2002, “TU 11: A Collection of Rules for the
- Prediction of Lunar Phases and of Month Lengths”, SCIAMVS 3, 3–90, J. M. Steele
- Late Babylonian procedure texts for gnomons ,Mathieu Ossendrijver – 12 february 2014
- Astronomical Instruments In Ancient India, Shekher Narveker,June, 2007,esp.shanku, gnomon
- Early Indian Astronomy by George Abraham
- Hindu Astronomy
- Neugebauer and Pingree, The Pancasiddhantika of Varahamihira vol 1 1970
- Sanskrit Astronomical Tables In England ( Manuscripts) David Pingree
- Astral Sciences In Mesopotamia Hermann Hunger & David Pingree 1999 ( BRILL)
More References from Stack A:
- A Geometric Algorithm with Solutions to Quadratic Equations
- in a Sumerian Juridical Document from Ur III Umma
- Joran Friberg, Chalmers University of Technology, Gothenburg, Sweden
- Geometric division problems, quadratic equations, and recursive
- geometric algorithms in Mesopotamia,Joran Friberg
- google search engine <Trapezoid area bisection>
- Wikipedia search engine <Trapezoid area >
- mathworld.wolfram.com, Trapezoid and right trapezoid
- Mathematical Treasure: Old Babylonian Area Calculation, uses ancient method
- Frank J. Swetz , Pennsylvania State University
- Wikipedia, see temple of Edfu, area method used as late as 200 BC in Egypt.
- Oneliner's Pie in the Sky
- One Liners
- Category Algorithm
- Babylonian Number Series and eTCL demo example calculator
- Brahmagupta Area of Cyclic Quadrilateral and eTCL demo example calculator
- Babylonian Trapezoid Bisection Algorithm and eTCL demo example calculator, numerical analysis
- Chinese Horse Race Problems from Suanshu, DFP, and example eTCL demo calculator, numerical analysis
- Gauss Approximate Number of Primes and eTCL demo example calculator
- Land surveying in ancient Mesopotamia, M. A. R. Cooper
- Sumerian Approximate Area Quadrilateral and eTCL Slot Calculator Demo Example , numerical analysis
- Thomas G. Edwards, Using the Ancient Method of False Position to Find Solutions
- Joy B. Easton, rule of double false position
- Vera Sanford, rule of false position
- www.britannica.com, topic, mathematics trapezoid
- Sumerian Equivalency Values, Ratios, and the Law of Proportions with Demo Example Calculator
- Babylonian Sexagesimal Notation for Math on Clay Tablets in Console Example
- Babylonians Tracked Jupiter With Advanced Tools: Trapezoids, Michael Greshko, news.nationalgeographic.com
- Geometry in Babylonian Astronomy, Cluster of Excellence Topology, Humboldt University of Berlin
- Mathieu Ossendrijver: „Ancient Babylonian astronomers calculated Jupiter’s position
- from the area under a time-velocity graph“, in: Science, January 29, 2016.
- Late Babylonian Field Plans in the British Museum, books.google.com/books
- Karen Rhea Nemet-Nejat
- Late Babylonian Surface Mensuration Author(s): Marvin A. Powell Source: jstor
- translation: trapezoid in two babylonian astronomical cuneiform
- texts for jupiter (act 813 & act 817) from the seleucid era , 310 BC -75 AD
- Otto Neugebauer, Astronomical Cuneiform Texts, 3 Vols.
- Lund Humphreys, London, 1955:405,430-31.
- DeSegnac, MS 3908 A RE-CONSTRUCTION, D.A.R. DeSegnac
- A draft for an essay
- DeSegnac, MENTAL COMPUTING OF THREE ARCHAIC
- MESOPOTAMIAN PUZZLES W 20044, 35, W 20044, 20 & W 20214, essay draft
- DeSegnac, HARMONY OF NUMBERS I and II, D.A.R. DeSegnac, A draft for an essay
More References from Stack B.
- The Marduk Star Nēbiru, Immanuel Freedman,Cuneiform Digital Library Bulletin 2015:3, 8 November 2015
- Computing planetary positions - a tutorial with worked examples, webpage By Paul Schlyter, Stockholm, Sweden
- New perspective on the Exaltation of Planets, Blog of Kiril Stoychev, Bulgarian Astrological Association, December
- 20, 2015
- Probability for Lunar Occultation, for maximum distance from the ecliptic, note by dotancohen, Apr 7 2014,
- Mathematics Stack Exchange
- Babylonian Mathematical Astronomy, Chapter, January 2015, Mathieu Ossendrijver, Freie Universität Berlin
- Babylonian Market Predictions, Chapter on April 2019, Mathieu Ossendrijver, Freie Universität Berlin
- BM 32339+32407+32645 - New Evidence for Late Babylonian Astrology.
- Chapter on September 2018, Mathieu Ossendrijver,
- Freie Universität Berlin
- Ancient Babylonians took first steps to calculus, article By Ron Cowen, Science magazine, 29Jan2016
- Ancient Babylonian astronomers calculated Jupiter’s position from the area under a time-velocity graph,
- Article by Mathieu Ossendrijver, Science magazine, 29Jan2016
- Babylonian mathematical astronomy procedure texts, bibliography
- Babylonian astronomy, Wikipedia, collected 2020
- Babylonian and Indian Astronomy: Early Connections, Subhash Kak, February 17, 2003
- Electrical & Computer Engineering, Louisiana State University, Baton Rouge, LA
- Babylonian Trapezoid Bisection Algorithm and eTCL demo example calculator, numerical analysis
- Babylonian Field Expansion Procedure Algorithm and example demo eTCL calculator, numerical analysis
- Article by Mathieu Ossendrijver, mathematical terminology in Babylonian astronomical texts, 2012
- Babylonian False Position Algorithm and eTCL demo example calculator, numerical analysis
- Babylonian Combined Market Rates and eTCL demo example calculator, numerical analysis
- Babylonian Brothers Inheritance Problems Algorithm and eTCL demo example calculator, numerical analysis
- Babylonian Cubic Equation Problem and eTCL demo example calculator, numerical analysis
- Sumerian Base 60 conversion and eTCL demo example calculator, numerical analysis
- Aryabhat Sum of Squares and Cubes and eTCL demo example calculator, numerical analysis
- Sumerian Approximate Area Quadrilateral and eTCL Slot Calculator Demo Example , numerical analysis
- Article by Mathieu Ossendrijver, Babylonian-computational-astronomy-print.pdf, 2012
- Babylonian Astronomy in Context,
- Keeping the Watch: Babylonian Astronomical Diaries and More, Mathieu Ossendrijver
- Humboldt University Berlin, April 3 2018
- Exploring Jupiter: The Astrological Key to Progress, Prosperity & Potential,
- 310 Pages , 1996 by Stephen Arroyo
- A Primer on Logarithms by Shailesh Shirali, Mathematical Marvels Universities Press
- Studies on the Ancient Exact Sciences in Honor of Lis Brack-Bernsen, eds John M. Steele
- Mathieu Ossendrijver
- A study of Babylonian planetary theory, subtitle The outer planets, by Teije de Jong1
- date 31 August 2018
- Under One Sky: Astronomy and Mathematics in the Ancient Near East
- Author(s): John M. Steele, Annette Imhausen, Publisher: Ugarit-Verlag, Year: 2002
- Rising Time Schemes in Babylonian Astronomy, Author(s): John M. Steele, Publisher: Springer, Year: 2017
- Observation, theory and practice in late Babylonian astronomy: Some preliminary observations, Author(s): Steele J.
- Ancient astronomy and celestial divination, Author(s): N M Swerdlow
- The Babylonian theory of the planets, Author(s): Noel M. Swerdlow,
- Publisher: Princeton University Press, Year: 1998
- Administrative Timekeeping in Ancient Mesopotamia, Robert Englund,
- Journal of the Economic and Social History of the Orient 31 (1988) 121-185
- Bisectable Trapezia in Babylonian Mathematics, Lis Brack Bernsen,Olaf Schmidt
- First published: April 1990
Table, Math Terms Associated with Babylonian Trapezoids
| Table , Math Terms Associated with Babylonian Trapezoids | printed in tcl format | modern equivalent, English | comment if any | |
|---|---|---|---|---|
| sag ki.gu : | side earth | trapezoid | ||
| sag ki.ta : | side earth its , possessive case | upper front of the trapezoid | ||
| sag an.na : | side upper | upper front of the trapezoid | ||
| us gi.na : | length front | true length of the trapezoid | ||
| sag gi.na : | side front | true front of trapezoid | ||
| N1 kus i-ku-lu : | N1 cubit in eats it (it or man), read left to right | feed parameter of the trapezoid | noun derived from Sumerian SOV phrase | |
| sag du : | side | triangle | ||
| N1 arakarum : | N1 multiply | transformation coefficient, usually scale up |
Note. These Math Terms cover 4 or 5 cuneiform languages, and 5000 years of history. Math Terms are best understanding of context and math connotation here,not blessed by linguists and cuneiform dictionaries.
Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# Stick Shadow Time From VEDIC Math
# written on windows XP on eTCL
# working under TCL version 8.6
# gold on TCL CLUB , 14jun2014
# comment follows from gold, 12Jul2020
# pretty print from autoindent and ased editor
# Stick Shadow Time From VEDIC Math V2
# written on Windows 10 on TCL
# working under TCL version 8.6
# Revamping older program from 2014.
# One of my early TCL programs on wiki.
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
#package require math::combinatorics
#namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {shadow length <@ tx> centimeters:} }
lappend names {vertical stick length centimeters (gnomon usually constant):}
lappend names {noon shadow length <@ t12> centimeters:: }
lappend names {Vedic formula constant usually 1: }
lappend names {answers: quantity or ratio d/2t: }
lappend names {quantity or ratio t/d:}
lappend names {quantity or ratio s/g: }
lappend names {Vedic time estimate >> function(s/g): }
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Babylonian Shadow Length V2
from TCL ,
# gold on TCL Club, 12Dec2018 "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg " Stick Shadow Time From VEDIC Math V2
from TCL Club ,
# self help listing
# problem, Stick Shadow Time From VEDIC Math V2
# 3 givens follow.
1) shadow length <@ t1> centimeters:
2) vertical stick length centimeters
3) noon shadow length <@ t12> centimeters:
# Recommended procedure is push testcase
# and fill frame,
# change first three entries etc, push solve,
# and then push report.
# Report allows copy and paste
# from console to conventional texteditor.
# For testcases, testcase number is internal
# to the calculator and will not be printed
# until the report button is pushed
# for the current result numbers.
# >>> copyright notice <<<
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK license terms.
# Editorial rights and disclaimers
# retained under the TCL/TK license terms
# and will be defended as necessary in court.
Conventional text editor formulas
or formulas grabbed from internet
screens can be pasted into green console.
# gold on TCL Club, 12Dec2018 "
tk_messageBox -title "Self_Help" -message $msg }
proc pi {} {expr 1.*acos(-1)}
proc radianstodegconst {} {return [/ 180. [pi] ] }
proc xradianstodegconst {} {return [/ [pi] 180. ] }
proc degz {} {return [/ 180. [pi] ]}
proc degx {aa} {return [ expr { [degz]*atan($aa) } ]}
proc precisionx {precision float} {
# tcl:wiki:Floating-point formatting, <AM>
# select numbers only, not used on every number.
set x [ expr {round( 10 ** $precision * $float) / (10.0 ** $precision)} ]
# rounded or clipped to nearest 5ird significant figure
set x [ format "%#.5g" $x ]
return $x
}
# following procs invoke TCLLIB
proc pyramid_d {hh bb} { [ acotand [expr (.5*$bb/$hh) ]] }
proc pyra_d {hh bb} { [ acotand [* .5 [/ $bb $hh] ]] }
# pyramid_degrees 57.692 106.346 answer 47.334157521261254
# seked = (7 * .5 * 360 cubits) / 250 cubits = 5.04 decimal palms
proc seked_d {hh bb} { [/ [* 7. .5 $bb ] $hh ] }
# usage seked 250. 360. equals 5.04
# end TCLLIB
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8 testcase_number
global length0 shadow
incr testcase_number
set $side1 [* $side1 1. ]
set $side2 [* $side2 1. ]
set $side3 [* $side3 1. ]
set $side4 [* $side4 1. ]
set $side5 [* $side5 1. ]
set stick_shadow $side1
set gnomon_length $side2
set noon_shadow $side3
# formula constant usually integer 1
set constant $side4
set time_fraction [expr {($stick_shadow - $noon_shadow)/$gnomon_length + $constant } ]
set shadow_over_gnomon [/ $stick_shadow $gnomon_length]
set fraction_t_over_d [ expr { (1./2.)*(1./$time_fraction ) } ]
set side5 $time_fraction
set side6 $fraction_t_over_d
set side7 $shadow_over_gnomon
set side8 $time_fraction
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8} {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8 testcase_number
global length0 shadow
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Stick Shadow Time From VEDIC Math Report, screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
console show;
puts "%|table| printed in|TCL format |% "
puts "&|testcase number:| $testcase_number| |& "
puts "&|shadow length <@ tx> centimeters:| $side1| |& "
puts "&|vertical stick length centimeters (gnomon usually constant): |$side2| |& "
puts "&|noon shadow length <@ t12 : |$side3| |& "
puts "&|Vedic formula constant usually 1: | $side4| |& "
puts "&|quantity or ratio d/2t | $side5| |& "
puts "&|quantity or ratio t/d: | $side6| |& "
puts "&|quantity or ratio s/g: | $side7| |& "
puts "&|Vedic time estimate >> function(s/g): | $side8| |& "
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 100. 100. 1. 1.0 2. 2. 1. 2.}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 100. 100. 1. 1.0 2. 2. 1. 2. }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 100. 100. 1. 1.0 2. 2. 1. 2. }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command about
::ttk::button .self_help -text self_help -command { self_help }
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Stick Shadow Time From VEDIC Math V2" Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
Console program under test.
Expansion subroutine
gold - 2020-07-5
# console program written on Windows 10
# working under TCL version 8.6
# gold moniker on TCL WIKI , 7jul2020
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
proc expansion_procedure_2 { side1 side2 side3 side4 side5 epsilon } {
set counter 1
set token1 $side1
set token2 $side2
set token3 $side3
set epsilon [/ 1. $side5]
puts " %| Table of Natural Log and Round_off |% "
puts " %| counter | value | rounded value | ln | round off | round off |% "
while { $counter < 30. } {
#if { [abs [- $side4 [* $token1 $token2 $token3 1. ] ] ] < $epsilon } {break;}
#if { [- $side4 [* $token1 $token2 $token3 1. ] ] > 0 } {set correction_fraction [* 1. [/ 1. $side5] ]}
#if { [- $side4 [* $token1 $token2 $token3 1. ] ] < 0 } {set correction_fraction [* -1. [/ 1. $side5] ]}
#set correction_fraction [- $side3 [* $token1 $token2 1. ] ]
incr counter
set token1 [ expr ($token1 + .1 ) ]
set token2 [ expr (log ($token1)) ]
set round_off [format %7.2f $token2 ]
set value_rounded [format %7.2f $token1 ]
puts " &| $counter | $token1 | $value_rounded | $token2 | $round_off | $round_off |& "
} }
set side8 [ expansion_procedure_2 1.0 1.0 1.0 1000. 10. 1. ]
# printoutprintout
# pretty print from autoindent and ased editor
# Babylonian Expansion Procedure Algorithm Calculator V2
# console program written on Windows 10
# working under TCL version 8.6
# TCL WIKI , 2jul2020
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
proc expansion_procedure2 { side1 side2 side3 side4 side5 epsilon } {
set counter 1
set token1 $side1
set token2 $side2
set token3 $side3
set saver1 .00001
set saver2 .00001
set saver3 .00001
set epsilon [/ 1. $side5]
while { $counter < 1000. } {
if { [abs [- $side4 [* $token1 $token2 $token3 1. ] ] ] < $epsilon } {break;}
if { [- $side4 [* $token1 $token2 $token3 1. ] ] > 0 } {set correction_fraction [* 1. [/ 1. $side5] ]}
if { [- $side4 [* $token1 $token2 $token3 1. ] ] < 0 } {set correction_fraction [* -1. [/ 1. $side5] ]}
#set correction_fraction [- $side3 [* $token1 $token2 1. ] ]
set token1 [+ $token1 $correction_fraction ]
set token2 [+ $token2 $correction_fraction ]
set token3 [+ $token3 $correction_fraction ]
incr counter
puts " &| token1 | $token1 | token2 | $token2 | token3 | $token3 | product | [* $token1 $token2 $token3 ] | correction | $correction_fraction |& "
} }
set side8 [ expansion_procedure_2 9.6 9.6 9.6 1000. 60. .15 ]
# printout followsTable of Natural Log and Round_off
| Table of Natural Log and Round_off | |||||
|---|---|---|---|---|---|
| table | printed in | tcl wiki format | |||
| quantity | value | comment, if any | |||
| quantity | value | comment, if any | |||
| counter | value | rounded value | ln | round off | round off |
| 2 | 1.1000000000000001 | 1.10 | 0.095310179804324935 | 0.10 | 0.10 |
| 3 | 1.2000000000000002 | 1.20 | 0.18232155679395479 | 0.18 | 0.18 |
| 4 | 1.3000000000000003 | 1.30 | 0.26236426446749128 | 0.26 | 0.26 |
| 5 | 1.4000000000000004 | 1.40 | 0.33647223662121317 | 0.34 | 0.34 |
| 6 | 1.5000000000000004 | 1.50 | 0.40546510810816466 | 0.41 | 0.41 |
| 7 | 1.6000000000000005 | 1.60 | 0.47000362924573591 | 0.47 | 0.47 |
| 8 | 1.7000000000000006 | 1.70 | 0.53062825106217071 | 0.53 | 0.53 |
| 9 | 1.8000000000000007 | 1.80 | 0.58778666490211939 | 0.59 | 0.59 |
| 10 | 1.9000000000000008 | 1.90 | 0.64185388617239525 | 0.64 | 0.64 |
| 11 | 2.0000000000000009 | 2.00 | 0.69314718055994573 | 0.69 | 0.69 |
| 12 | 2.100000000000001 | 2.10 | 0.74193734472937778 | 0.74 | 0.74 |
| 13 | 2.2000000000000011 | 2.20 | 0.78845736036427061 | 0.79 | 0.79 |
| 14 | 2.3000000000000012 | 2.30 | 0.83290912293510455 | 0.83 | 0.83 |
| 15 | 2.4000000000000012 | 2.40 | 0.87546873735390041 | 0.88 | 0.88 |
| 16 | 2.5000000000000013 | 2.50 | 0.91629073187415555 | 0.92 | 0.92 |
| 17 | 2.6000000000000014 | 2.60 | 0.9555114450274369 | 0.96 | 0.96 |
| 18 | 2.7000000000000015 | 2.70 | 0.993251773010284 | 0.99 | 0.99 |
| 19 | 2.8000000000000016 | 2.80 | 1.0296194171811588 | 1.03 | 1.03 |
| 20 | 2.9000000000000017 | 2.90 | 1.0647107369924289 | 1.06 | 1.06 |
| 21 | 3.0000000000000018 | 3.00 | 1.0986122886681102 | 1.10 | 1.10 |
| 22 | 3.1000000000000019 | 3.10 | 1.1314021114911013 | 1.13 | 1.13 |
| 23 | 3.200000000000002 | 3.20 | 1.1631508098056815 | 1.16 | 1.16 |
| 24 | 3.300000000000002 | 3.30 | 1.1939224684724352 | 1.19 | 1.19 |
| 25 | 3.4000000000000021 | 3.40 | 1.2237754316221163 | 1.22 | 1.22 |
| 26 | 3.5000000000000022 | 3.50 | 1.2527629684953687 | 1.25 | 1.25 |
| 27 | 3.6000000000000023 | 3.60 | 1.2809338454620649 | 1.28 | 1.28 |
| 28 | 3.7000000000000024 | 3.70 | 1.3083328196501793 | 1.31 | 1.31 |
| 29 | 3.8000000000000025 | 3.80 | 1.3350010667323406 | 1.34 | 1.34 |
| 30 | 3.9000000000000026 | 3.90 | 1.3609765531356015 | 1.36 | 1.36 |
Comments Section
Please place any comments here, Thanks.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |