Version 8 of Creating Circles and Arcs in the Gnocl Canvas
Updated 2010-04-10 22:06:37 by wjgWJG (05/03/10) The gnocl canvas has no direct support for arc, is that odd? Not really, examination of the source for the Gnome Canvas shows that the ellipse is in fact a bezier circle. So, not only is this an approximation to a circle but the creation of arcs is going to be a nightmare. Ok, I've seen it done on Graphics apps such as animation systems using nurbs modelling, but we want to avoid curves as much as possible! Heres a simple, solution on the scripting side. Build a list of coordinates that generate a circle or arc and pass these to the gnocl::canvas object line command. This will create a suitable polyline. Here's a sample script that I've just puts together which does the job. Notice too, that the segments count for the arc is dependent upon the angle sweep. This could be modified to take into account the radius of the curve of the object if needed.
Here's the screenshot:
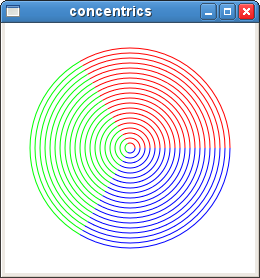
So, here's the script:
#!/bin/sh
# the next line restarts using tclsh \
exec tclsh "$0" "$@"
package require Gnocl
package require GnoclCanvas
# convert degs to rads
proc rads {a}{return[expr $a * 0.017453333] ;# ie PI/180}
# x,y co-ordinates of the centre of the arc
# r radius of the arc
# a1 angle of start point
# a2 angle of subtended by the arc
# s minimum number of steps in the arc
proc poly_arc {x y r a1 a2 {s 4}} {
# calculate the number of segments
set j [expr $a2 / 5]
if {$j >= $s } {set s $j}
# calculate angle increment
set delta [expr $a2 / $s]
# create coordinates for the polyline
for {set da $a1} {$da <= [expr $a1+ $a2] } {incr da $delta} {
set x2 [expr $x + cos( [rads $da] ) * $r]
set y2 [expr $y - sin( [rads $da] ) * $r]
lappend coords $x2
lappend coords $y2
}
return $coords
}
set canv [gnocl::canvas -background white]
gnocl::window \
-width 250 \
-height 250 \
-child $canv \
-title concentrics \
-onDelete exit
foreach {ang clr} {0 red 120 green 240 blue} {
for {set i 100} {$i >= 5} {incr i -5} {
# draw the line
$canv create line \
-coords [poly_arc 125 125 $i $ang 120] \
-fill $clr \
-width 1 \
-tags "concentric"
}
}
gnocl::mainLoopIDG Apr. 10/2010 If there's a bezier primitive, it's quite easy to use this to produce circles and ellipses. See A. Riskus, Information Technology and Control, 35, 371 (2006). (But note that equations 9 seem cocked up)
WJG (10/04/10) Yes, the Gnome Canvas creates 'ellipses' using four Bezier curves. Calculating the right positions for the control nodes for all contingencies is probably more processor intensive than the old trigonometry.
IDG It's not too bad. Here's code to produce a general ellipse, approximated by 4 bezier curves. I can't remember why I chose such weird names for the internal variables, but just use the output list 4 points at a time to draw the 4 beziers.
`
proc bezier_ellipse_points {xc yc R r angle} {
# calculate the 12 points needed for 4-arc bezier approximation to
# ellipse defined by arguments. xc, yc are centre coordinates,
# R and r are major and minor radii, angle is angle in degrees between
# major axis of ellipse and x coordinate axis.
# external variable ::PV180 contains pi/180.
set M [expr {0.551784 * $R}]
set m [expr {0.551784 * $r}]
set c [expr {cos($angle * $::PV180)}]
set s [expr {sin($angle * $::PV180)}]
set xa [expr {$xc + $R * $c}]
set ya [expr {$yc + $R * $s}]
set xb [expr {$xc - $r * $s}]
set yb [expr {$yc + $r * $c}]
set xd [expr {$xc - $R * $c}]
set yd [expr {$yc - $R * $s}]
set xe [expr {$xc + $r * $s}]
set ye [expr {$yc - $r * $c}]
set x1 [expr {$xa - $m * $s}]
set y1 [expr {$ya + $m * $c}]
set x2 [expr {$xb + $M * $c}]
set y2 [expr {$yb + $M * $s}]
set x3 [expr {$xb - $M * $c}]
set y3 [expr {$yb - $M * $s}]
set x4 [expr {$xd - $m * $s}]
set y4 [expr {$yd + $m * $c}]
set x5 [expr {$xd + $m * $s}]
set y5 [expr {$yd - $m * $c}]
set x6 [expr {$xe - $M * $c}]
set y6 [expr {$ye - $M * $s}]
set x7 [expr {$xe + $M * $c}]
set y7 [expr {$ye + $M * $s}]
set x8 [expr {$xa + $m * $s}]
set y8 [expr {$ya - $m * $c}]
return [list $xa $ya $x1 $y1 $x2 $y2 $xb $yb $x3 $y3 $x4 $y4\
$xd $yd $x5 $y5 $x6 $y6 $xe $ye $x7 $y7 $x8 $y8]
}` WJG (10/04/10) Its worth taking a look at. My experiments always resulted in a slightly flattened circle.