GS - Iterated Function Systems (IFS) is a self-similar model introduced by Michael Barnsley to generate fractal images like fern leaf or other aesthetic natural shapes. Here is a script to draw some of them like Serpienski gasket or Von Koch curve.
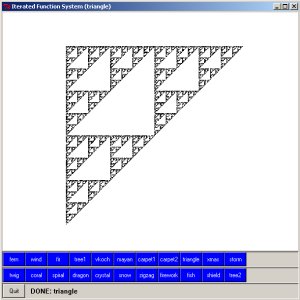
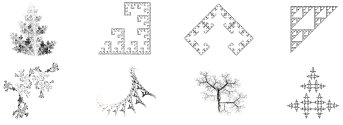
For more details about the theory behind IFS, see:
- Michael F. Barnsley, Fractals everywhere, Academic Press, 1993.
- H.-O. Peitgen, H. Juergens, D. Saupe, Chaos and Fractals: New Frontiers of Science, Springer-Verlag, 1992, Chapter 5.
# ifs.tcl
package require Tk
proc IFSMain { wd ht } {
set w .ifs
catch {destroy $w}
toplevel $w
wm withdraw .
wm title $w "Iterated Function System"
wm iconname $w "ifs"
wm geometry $w +100+10
set i 0
# Parameters
# 1st group: name of the fractal
# 2nd group: iterations, scale_x, scale_y, translation_x, translation_y
# 3rd group: coefficients for the affine transformation:
# x = a(i)x + b(i)y + e(i)
# y = c(i)x + d(i)y + f(i)
set tab {
{{fern} {24000 520 470 70 420} \
{0 0 0 .172 .496 -.091 0.076 .312 -.257 .204 .494 .133 \
0.821 -.028 .03 .845 .088 .176 -.024 -.356 -.323 .074 .47 .26}}
{{wind} {32000 80 140 30 440} \
{.3333 0 0 .3333 0 0 .1666 -.2886 .2886 .1666 3.3333 0 \
.1666 .2886 -.2886 .1666 5 2.8867 .3333 0 0 .3333 .6666 0}}
{{fir} {32000 460 480 110 470} \
{.65 -.013 .013 .65 .175 0 .65 -.026 .026 .65 .165 .325 \
0.318 -.318 .318 .318 .2 0 -.1666 .2886 .2886 .1666 .6666 0}}
{{tree1} {44000 1000 1000 300 480} \
{0 0 0 .5 0 0 0.42 -.42 .42 .42 0 .2 \
0.42 .42 -.42 .42 0 .2 0.1 0 0 .1 0 .2}}
{{vkoch} {10000 580 580 10 300} \
{0.3333 0 0 .3333 0 0 0.3333 0 0 .3333 .6666 0 \
0.1666 -.2886 .2886 .1666 .3333 0 -.1666 .2886 .28867 .1666 .6666 0}}
{{mayan} {19000 40 40 300 440} \
{.5 0 0 .5 -2.5634 -.000003 .5 0 0 .5 2.4365 -.000003 \
.0 -.5 .5 0 4.8730 7.5635}}
{{carpet1} {28000 420 400 90 440} \
{.333 0 0 .333 .333 .666 0 .333 1 0 .666 0 0 -.333 1 0 .333 0}}
{{carpet2} {19000 40 40 300 450} \
{0 -.5 .5 0 -1.7323 3.3661 .5 0 0 .5 -.0278 5.0148 \
0 .5 -.5 0 1.6208 3.3104}}
{{triangle} {22000 180 180 130 430} \
{.5 0 0 .5 0 0 .5 0 0 .5 0 1 .5 0 0 .5 1 1}}
{{xmas} {22000 400 400 100 450} \
{0 -.5 .5 0 .5 0 0 .5 -.5 0 .5 .5 .5 0 0 .5 .25 .5}}
{{storm} {12000 400 400 90 430} \
{0 .577 -.577 0 .0951 .5893 0 .577 -.577 0 .4413 .7893 \
0 .577 -.577 0 .0952 .9893}}
{{twig} {19000 600 600 30 530} \
{.387 .43 .43 -.387 .256 .522 .441 -.091 -.009 -.322 .4219 .5059 \
-.468 .2 -.113 .15 .4 .4}}
{{coral} {28000 43 43 300 450} \
{.3076 -.5314 -.4615 -.2937 5.402 8.6551 .3076 -.077 .1538 -.4475 -1.2952 4.153 \
0 .5454 .6923 -.1958 -4.8936 7.2697}}
{{spiral} {44000 38 38 300 440} \
{.7878 -.4242 .2424 .8598 1.7586 1.408 -.1212 .2575 .1515 .053 -6.7216 1.3772 \
.1818 -.1363 .091 .1818 6.0861 1.568}}
{{dragon} {34000 40 40 300 440} \
{.824 .2814 -.2123 .8641 -1.8823 -.1106 \
.0882 .521 -.4638 -.3777 .7853 8.0957}}
{{crystal} {36000 60 44 290 470} \
{.6969 -.481 -.394 -.6628 2.147 10.3102 \
.091 -.4431 .5151 -.0946 4.2865 2.9257}}
{{snow} {32000 500 500 40 520} \
{.255 0 0 .255 .3726 .6714 .255 0 0 .255 .1146 .2232 \
.255 0 0 .255 .6306 .2232 .37 -.642 .642 .37 .6356 -.0061}}
{{zigzag} {42000 40 40 310 450} \
{-.6324 -.6148 -.5453 .6592 3.8408 1.2823 \
-.0361 .4444 .2101 .037 2.071 8.3305}}
{{firework} {28000 40 40 300 450} \
{.7454 -.4591 .406 .8871 1.4602 .691 \
-.4242 -.0651 -.1757 -.2181 3.8095 6.7414}}
{{fish} {22000 40 34 300 420} \
{.3077 0 0 .2941 4.1191 1.6042 .1923 -.2058 .6538 .0882 -0.6888 5.979 \
.1923 .2058 -.6538 .0882 .6685 5.9625 .3077 0 0 .2941 -4.1365 1.6042 \
.3846 0 0 -.2941 -.0077 2.9411}}
{{shield} {22000 400 400 100 460} \
{.382 0 0 .382 .3072 .619 .382 0 0 .382 .6033 .4044 \
.382 0 0 .382 .0139 .4044 .382 0 0 .382 .1253 0.595 \
.382 0 0 .382 .492 .0595}}
{{tree2} {24000 410 410 80 430} \
{.195 -.488 .344 .443 .4431 .2452 .462 .414 -.252 .361 .2511 .5692 \
-.058 -.07 .453 -.111 .5976 .097 -.035 .7 -.469 -.022 .4884 0.507 \
-.637 0 0 .501 .8562 .2513}}
}
pack [canvas $w.c -width $wd -height $ht -bg white]
set f1 [frame $w.f1 -relief sunken -borderwidth 2]
pack $f1 -fill x
set f2 [frame $w.f2 -relief sunken -borderwidth 2]
pack $f2 -fill x
set n [expr {[llength $tab]/2}]
set f $f1
foreach l $tab {
set s [lindex [lindex $tab $i] 0]
button $f.b$i -text $s -width 5 \
-bg blue -fg white \
-command "IFS $w $s [list [lindex [lindex $tab $i] 1]] [list [lindex [lindex $tab $i] 2]]"
incr i
if {$i >= $n} then {set f $f2}
}
eval pack [winfo children $f1] -side left
eval pack [winfo children $f2] -side left
set f3 [frame $w.f3 -relief sunken -borderwidth 2]
pack $f3 -fill x
button $f3.bq -text Quit -width 5 -command exit
label $f3.lb -text " " -font system
eval pack [winfo children $f3] -side left
}
proc IFS { w s sparam fparam } {
array set m {}
set x0 0
set y0 0
$w.c delete all
[lindex [winfo children $w.f3] 0] configure -state disabled
[lindex [winfo children $w.f3] 1] configure -text " RUNNING: $s"
wm title $w "Iterated Function System ($s)"
set pix [image create photo]
set cmap #000000
$w.c create image 0 0 -anchor nw -image $pix
foreach {maxit mx my tx ty} $sparam {}
set j 0
foreach {m1 m2 m3 m4 m5 m6} $fparam {
incr j
set m($j,1) $m1
set m($j,2) $m2
set m($j,3) $m3
set m($j,4) $m4
set m($j,5) $m5
set m($j,6) $m6
}
for {set i 1} {$i <= $maxit} {incr i} {
set k [expr {int($j*rand() - 0.0001) + 1}]
set x [expr {$m($k,1)*$x0 + $m($k,2)*$y0 + $m($k,5)}]
set y [expr {$m($k,3)*$x0 + $m($k,4)*$y0 + $m($k,6)}]
set x0 $x
set y0 $y
if {$maxit > 10} then {
set X [expr {round([expr $mx*$x + $tx])}]
set Y [expr {round([expr -$my*$y + $ty])}]
$pix put $cmap -to $X $Y
update
}
}
[lindex [winfo children $w.f3] 0] configure -state normal
[lindex [winfo children $w.f3] 1] configure -text " DONE: $s"
}
IFSMain 600 480 ; # Screen size (x,y)