Version 223 of Indian Math Bhaskara (1) Sine formula and extensions, history of math
Updated 2018-01-22 21:29:52 by goldIndian math Bhaskara sine formula and extensions, History math
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER in your comment with the same courtesy that I will give you. Its very hard to reply intelligibly without some background of the correspondent. Thanks,gold
- Indian math Bhaskara sine formula and extensions, History math
- Introduction
- Bhaskara sine function of historical interest
- Bhaskara function and extensions into TCL code
- Console program for Bhaskara sine function
- Screenshots Section
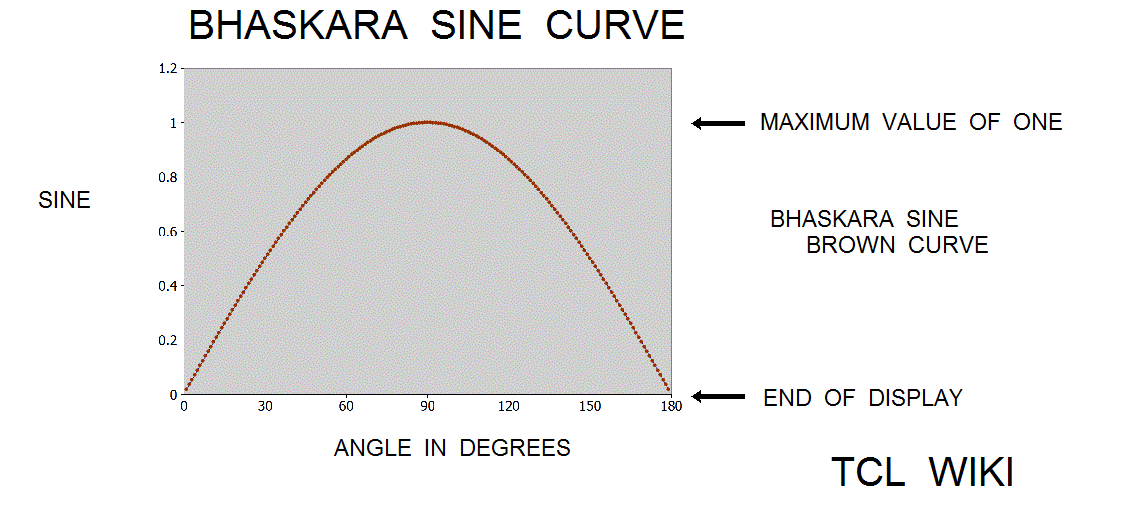
- figure 1. Original Bhaskara Sine with 40500 constant
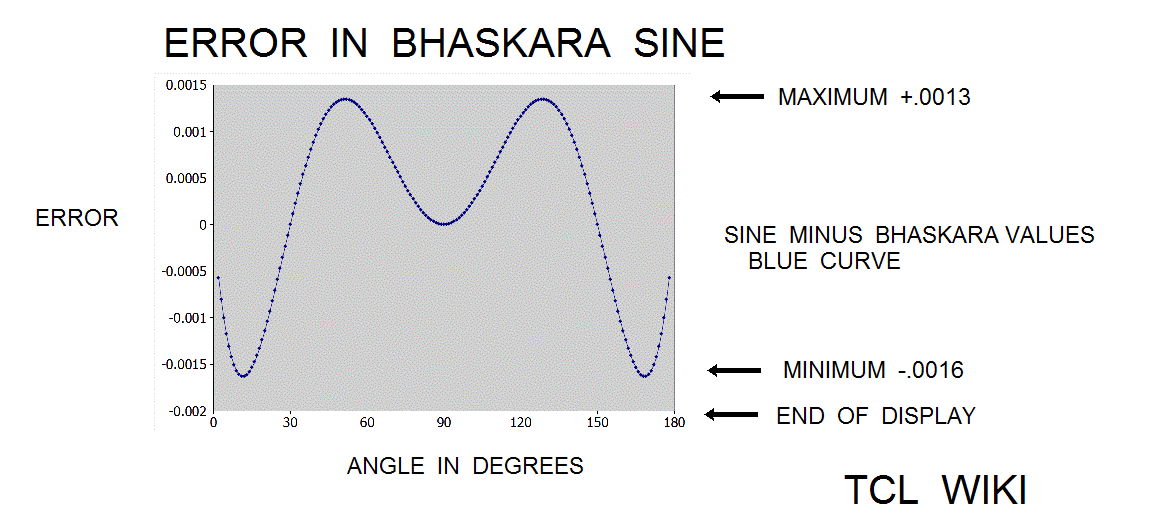
- figure 2. Error of Bhaskara Sine with 40500 constant
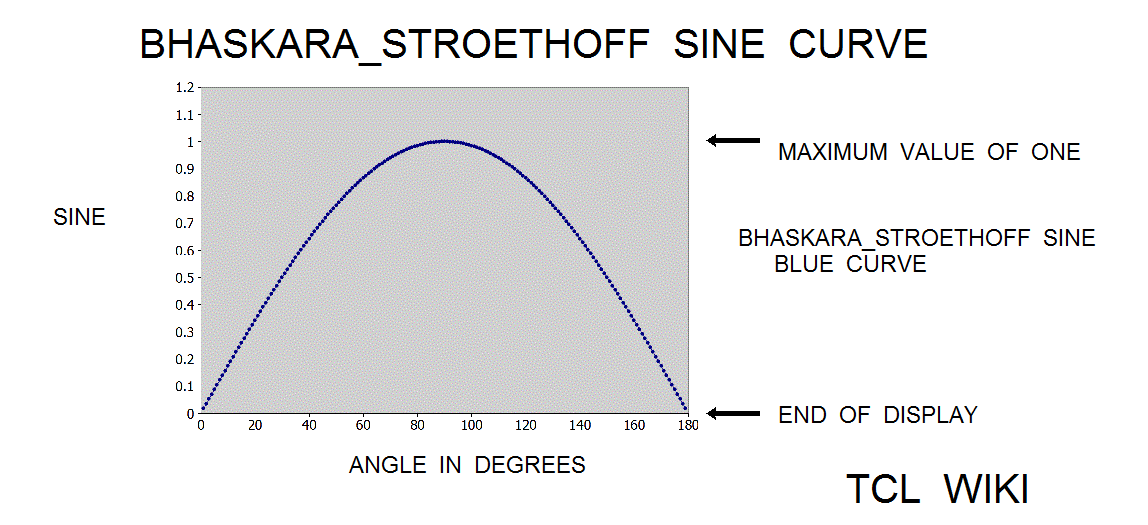
- figure 3. Bhaskar_Stroethoff Sine with corrective poly
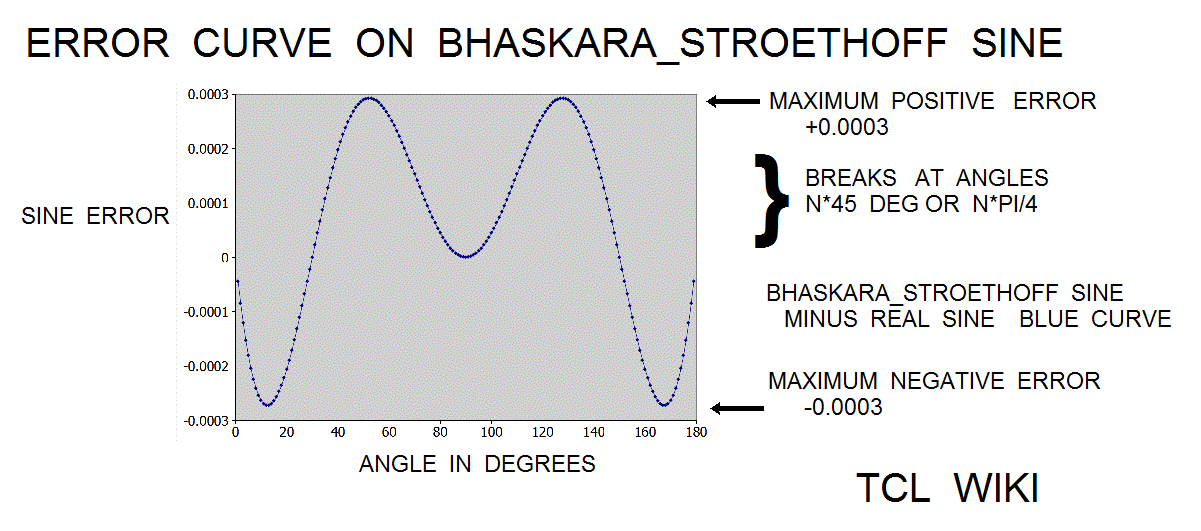
- figure 4. Error of Bhaskar_Stroethoff Sine with corrective poly
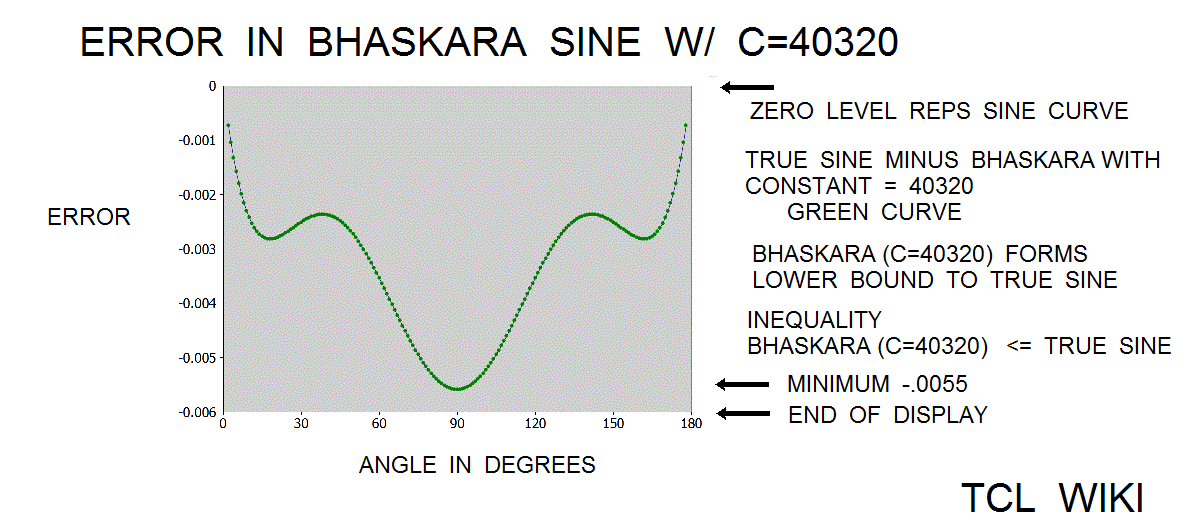
- figure 5. Error of Bhaskara Sine with 40320 constant
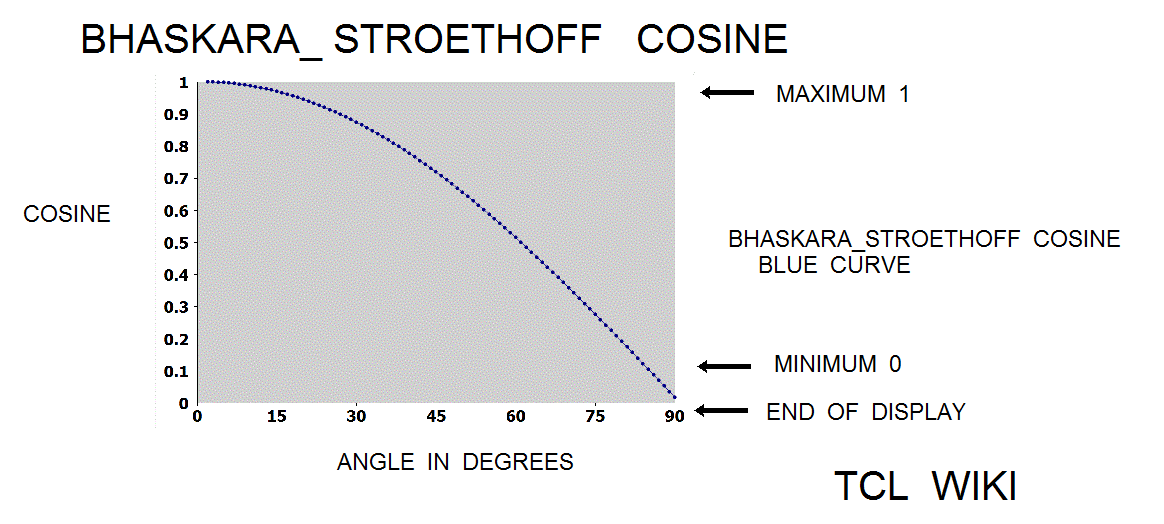
- figure 6. Bhaskara_Stroethoff Cosine
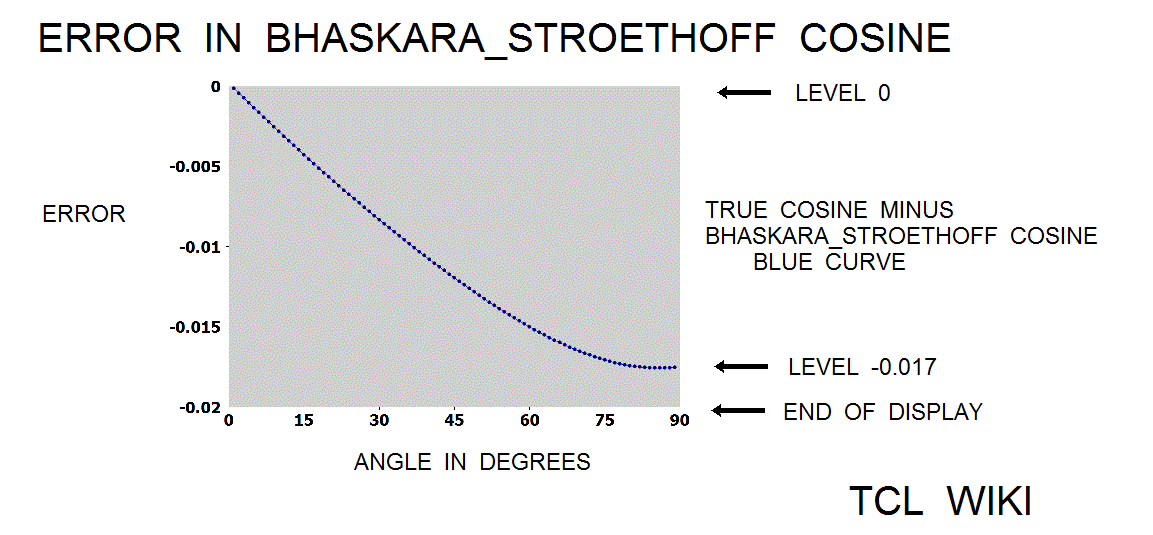
- figure 7. Bhaskara_Stroethoff Cosine Error
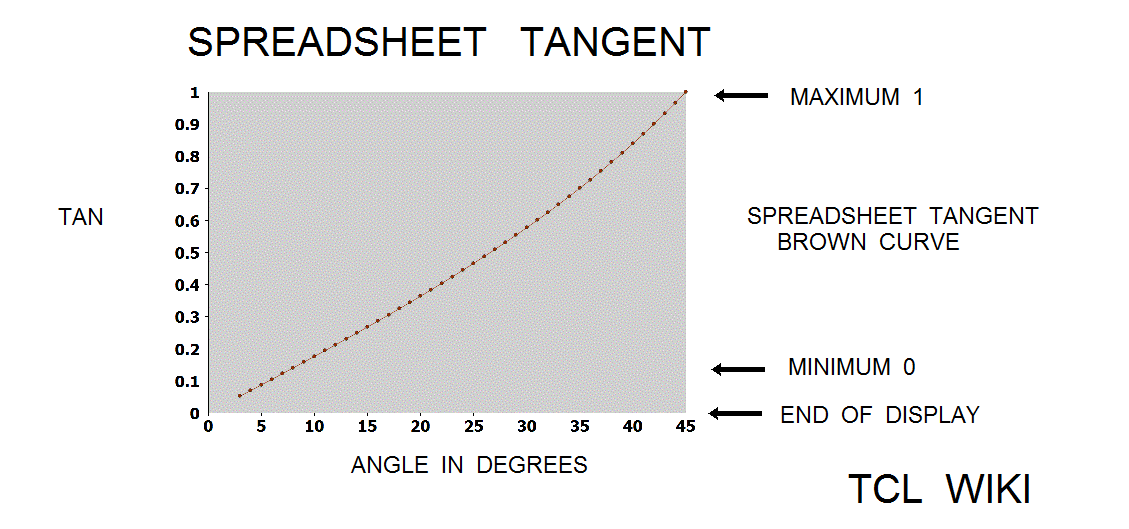
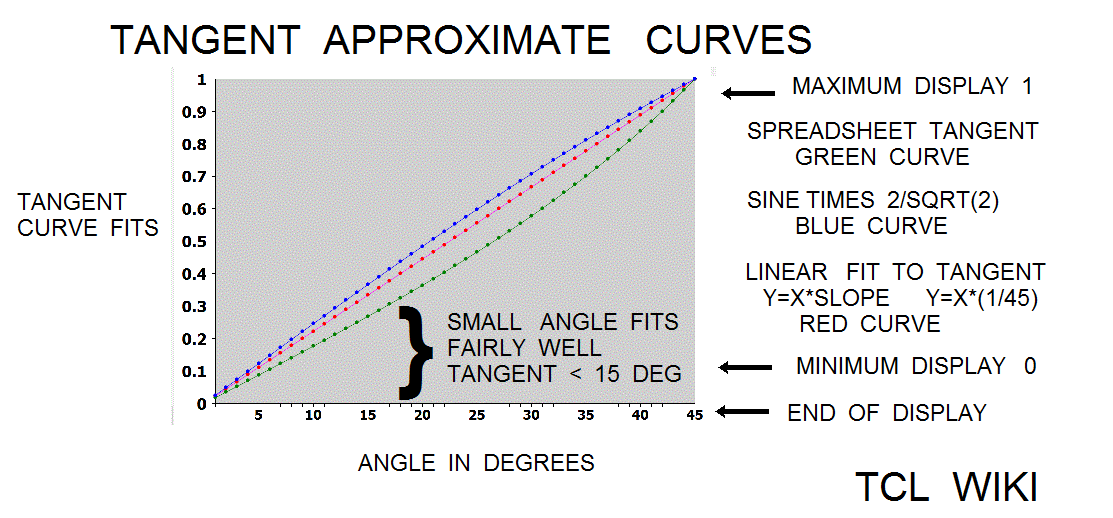
- figure 8. Spreadsheet tangent
- figure 9. Curve fits to spreadsheet tangent
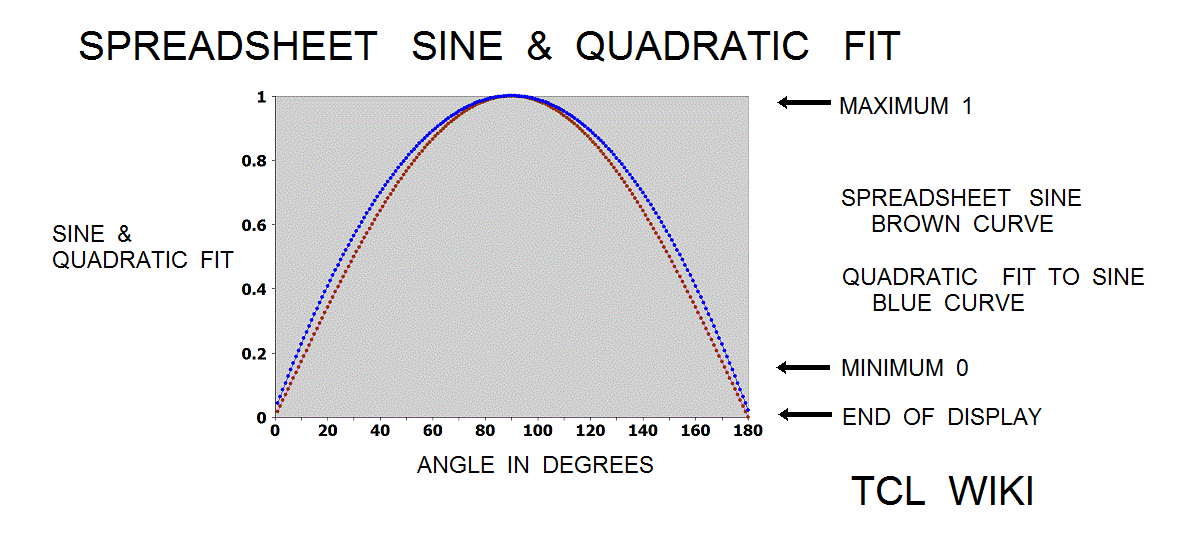
- figure 10. Quadratic Curve fits to spreadsheet sine
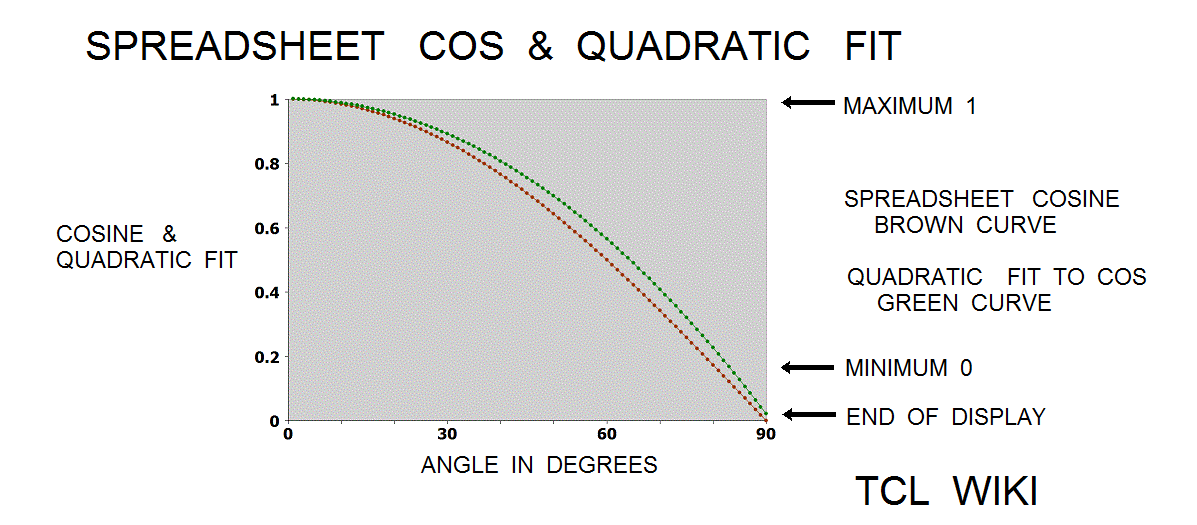
- figure 11. Quadratic Curve fits to spreadsheet cosine
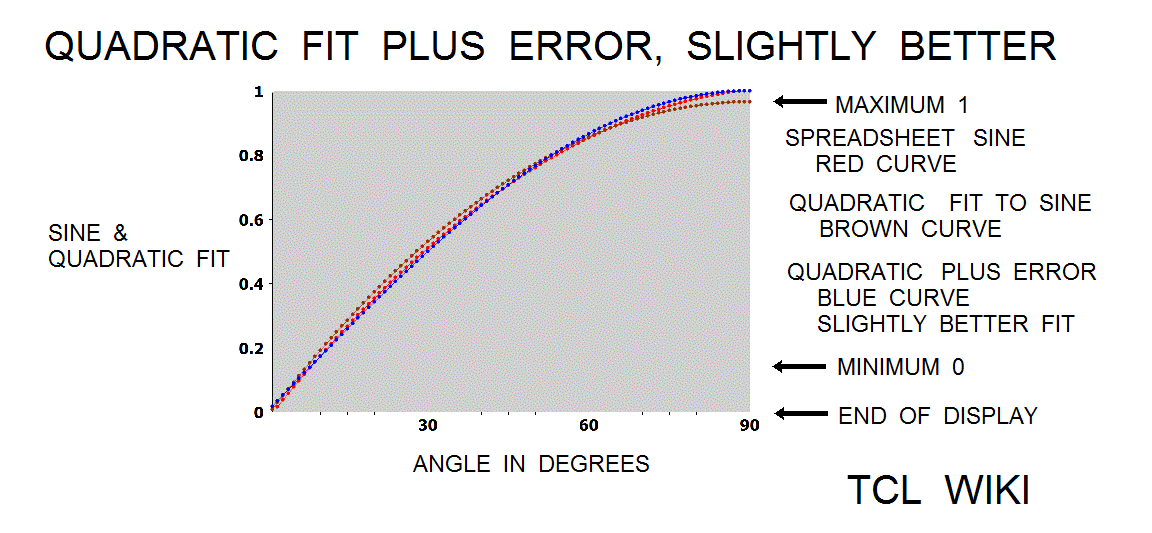
- figure 12. Quadratic Curve fit plus error curve, slightly better fit
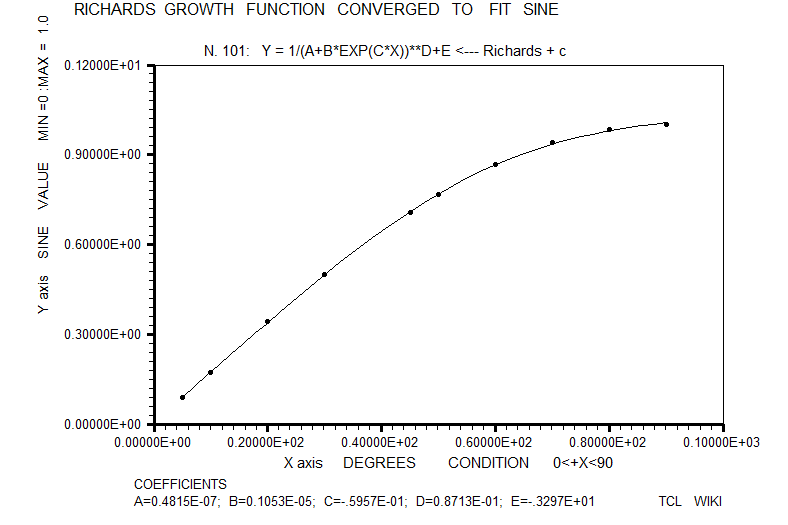
- figure 13. Richards growth function converged to sine
- figure 14. Richards growth function, plotted residuals
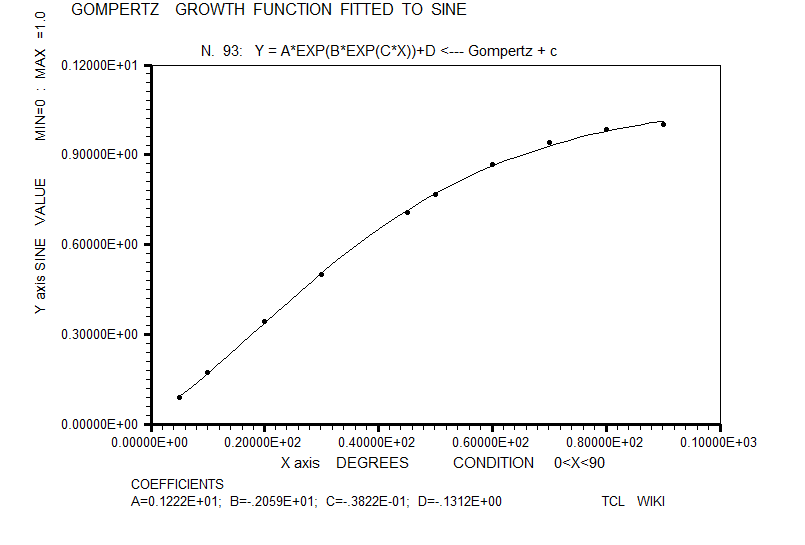
- figure 15. Gompertz growth function fitted to sine
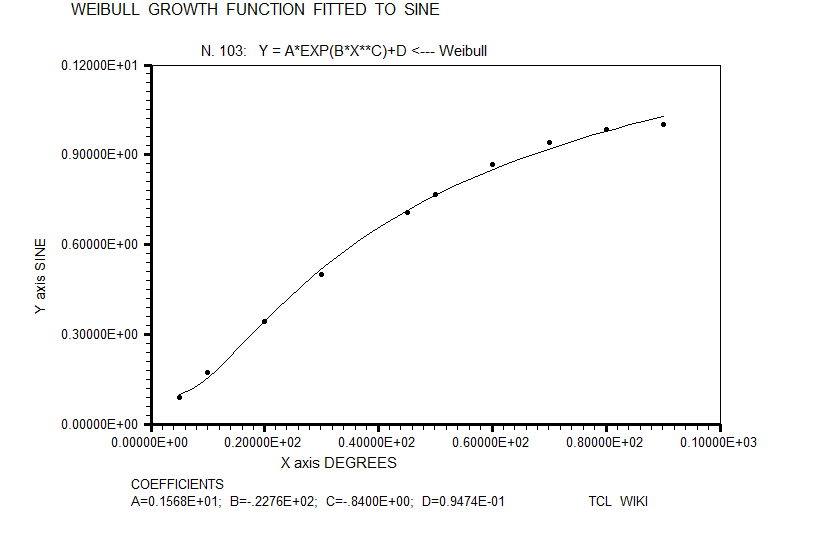
- figure 16. Weibull growth function fitted to sine
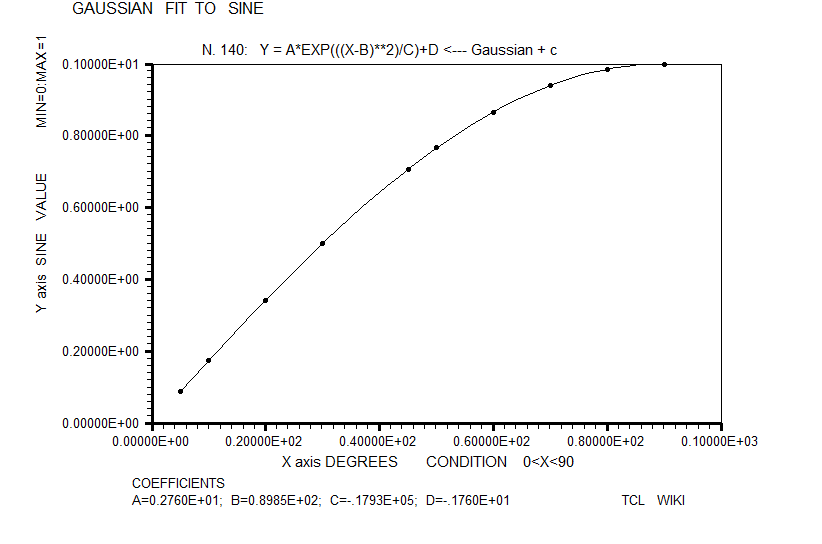
- figure 17. Gaussian growth function fitted to sine
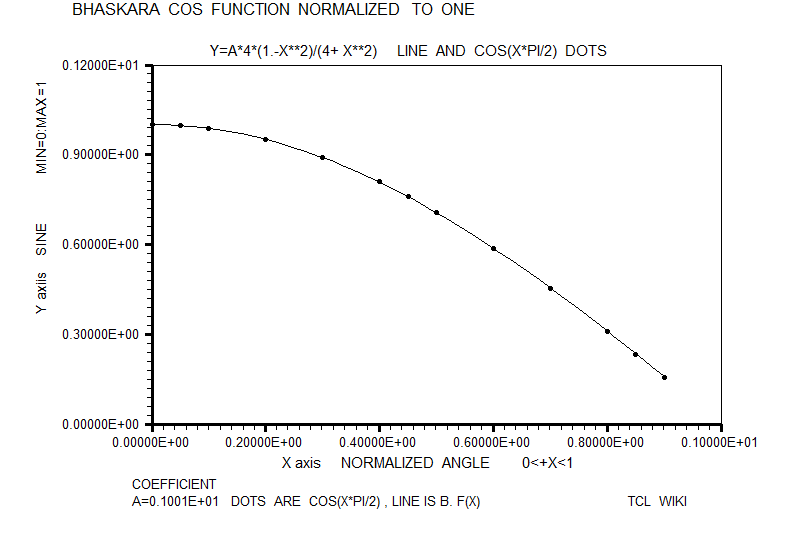
- figure 18. Bhaskara cosine formula normalized to one
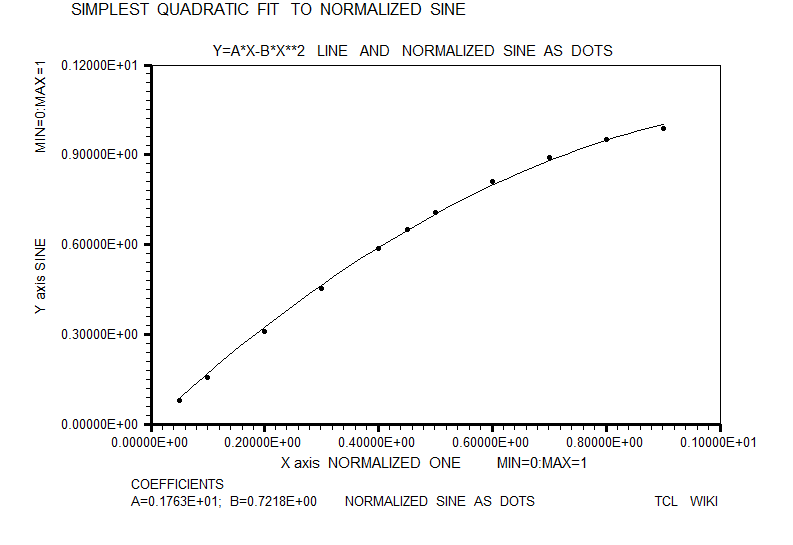
- figure 19. Simplest quadratic fit to sine, normalized to one
- figure 20. Fit to normalized sine curve
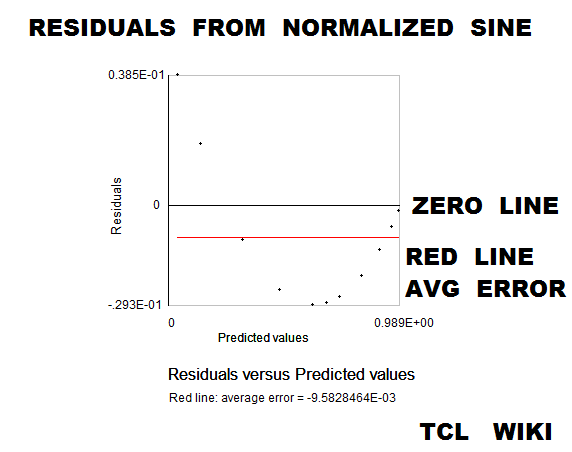
- figure 21. Residuals from fit to normalized sine
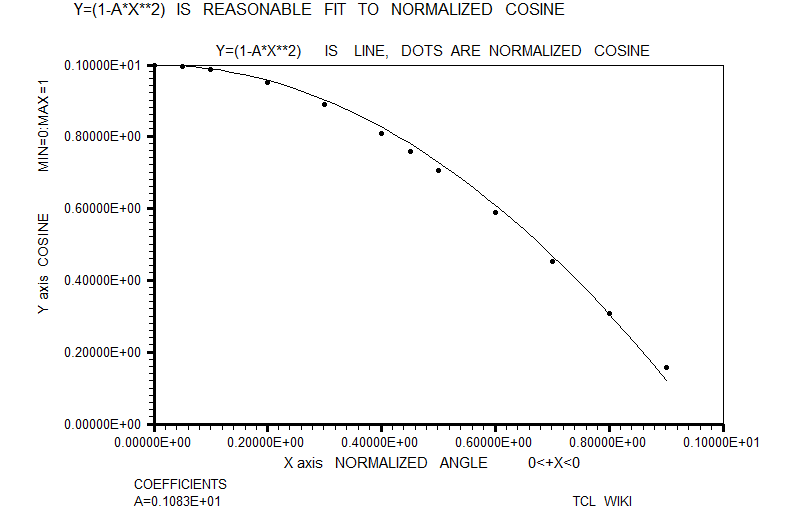
- figure 22. Fit to normalized cosine
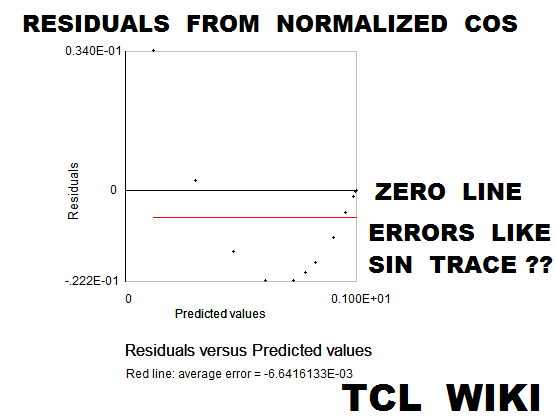
- figure 23. Residuals from fit to normalized cosine
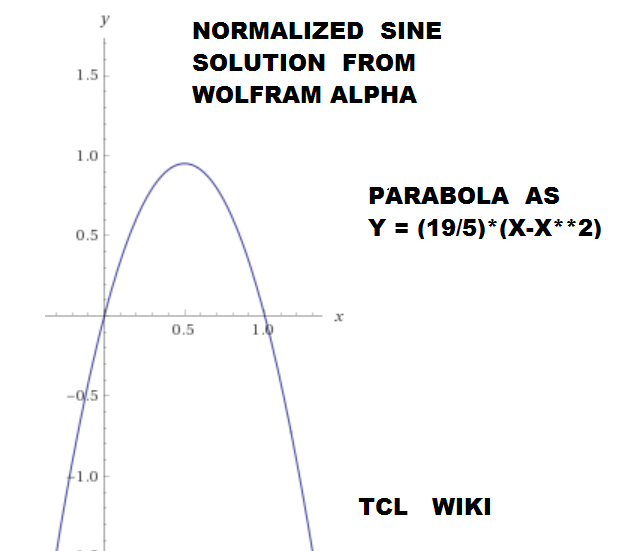
- figure 24. Wolfram solution to normalized sin
- Testcase 1
- Testcase 2
- Testcase 3
- Testcase 4
- References:
- Appendix Code
- Comments Section
Introduction
gold Here is some TCL starter code for Indian math Bhaskara sine formula and extensions. The Bhaskara sine formula is of historical interest, but has not been used since the era of the great Indian astronomers.
Bhaskara sine function of historical interest
The Bhaskara sine function or formula was the basis of sine tables edited by the Indian mathematician Bhaskara 1 in the seventh century. The Bhaskara sine function was possibly derived from the parabolic curve, from article in Mathematics Magazine by Dr . Shailesh A. Shirali. The Bhaskara sine formula and extended formulas are mostly for positive x < pi/2. Bhaskara used integers in the formula from the seventh century. Given the normal trig relations, the Bhaskara sine function can be extended to sind, cosd, tand in equivalence to the accuracy of 2nd order taylor series. As Dr . Shailesh A. Shirali demonstrated, the similarity of Bhaskara sine function to the Taylor and Pade formulas is worth some study. Often wondered whether the parabolic curve could be fudged into a sine or cosine curve.
Bhaskara function and extensions into TCL code
Details for loading TCL procedures. The Bhaskara sine function was extended into a set of TCL expressions into a catch-all TCL proc using degree measures. The original Bhaskara sine function used angle measurement in jotas, transformed into radians, and then transformed into cordics, according to the Shirali article. Here the formulas used the degree measures, although adaptations to radian measure are available. The Bhaskara sind was expr { (4.*$x*(180.-$x))/( 40500.-$x*(180.-$x)) }, for positive pi and 0>$x<pi. Dr. Shirali used the the identity cos(a)deg = sin(90-x) deg for the derived Bhaskara cosd of expr { (4.*(90.-$x))*(90.+$x)/( 32400.+$x*$x) }, -pi/2<$x>pi/2.
Continuing in a similar manner, the derived Bhaskara tand was expr { $bhaskara_sindx/$bhaskara_cosdx } and the derived Bhaskara tand was expr {$bhaskara_cosdx/$bhaskara_sindx }. The derived bhaskara_secdx was expr { ( 32400.+$x*$x)/(4.*(90.-$x))*(90.+$x) } and bhaskara_cscdx was expr { ( 40500.-$x*(180.-$x))/(4.*$x*(180.-$x)) } .
The Bhaskara step quadratic formulas and set up can be used to develop a crude tangent formula. These axioms were developed in the papers by Dr. Shirali , Stroethoff ,and Gupta. Some conditions are found in other Indian sutras: the sine tables were developed on a standard circle of 21600 minutes with a radius of 3438 minutes (for astronomy). The sind is sind(x) = x*(180-x)/8100. In polynomial P, the sind(P) = (4*P)/(5-P). The cosd is cosd(x) (90-x)+(180-(90-x)/8100. The tand is sind/cosd which expands to tand = (x*(180-x)/8100)/((90-x)+(180-(90-x)/8100). Reduction, tand = (x*(180-x)) /((90-x)*(90+x)). So far, these step equations have about an 8 percent error. Substituting P= x*(180-x)/8100 into sind = (4*P)/(5-P) gives the Bhaskara sine formula with 0.37 percent error. Boiling down pages of algebra, the Bhaskara sine formula is a quadratic equation of sind(x) = x*(180-x)/8100 that is evaluated in (4*P)/(5-P) at sind(30) = 1/2. A quadratic equation with solutions at 0 and 180 is transformed into an equation with solutions at 0,180,and 30 degrees. < The trial step equations in polynomial P are sin = (4*P)/(5-P);side ~ (5-P) - (4*P*4*P) / 4, cos ~ ((5-P) -(4*P*4*P)/4)/(5-P); tan ~ ((5-P) - (4*P*4*P) / 4)/((4*P)/(5-P)) >
In the Grahalaghava manuscript of 1520 CE, the Indian mathematician Ganesa Daivajna published the Bhaskara formula with a different constant of 40320 versus the original Bhaskara constant of 40500. The error curve derived from the true sine minus formula(cc=40320) is largely negative, meaning the values of formula(cc=40320) are mostly above the true sine curve. As an inequality, true sine. <= formula(cc=40320) . Now compare the error curve derived from true sine minus formula(cc=40500), which does pass several times through the zero level representing the true sine. But the formula(cc=40500) is mostly positive and below true sine over the interval from 45 degrees (pi/4) to 135 degrees (3*pi/4). Thus in the region of greatest interest, the true sine lies between formula(cc=40500) and formula(cc=40350 )!! With conditions, the inequality exists that formula(cc=40500) <= true sine <= formula(cc=40350), over interval of (pi/4) to (3*pi/4).
There are several ways to estimate an optimal constant in the Blaskara sine formula. Roughly the optimal constant is in a band between 40400 and 40500, based on trial and error at setting input angle aa at 45 degrees or pi/4. The error curve of cc = 40500 has maximum of +.0013 and minimum of -0.0016, average ABS extremes would be (0.0013+0.0016)/2 or 0.00145. Setting extremes to average 0.00145, cc = 40500 * (0.70710678-0.00145)/0.70710678,40416.95. The formula(cc=40417) had relative error of 0.068 percent versus the relative error of 0.173 percent on the original formula(cc=40500). The formula(cc=40417) gave roughly about 0.173/0.068 or 2.5 times improvement in relative error. But will continue to study the error bounds.
A least squares method was fit to the sine curve with some known initial points from the small sine table. The 5 points were (0,0),(30,.5),(90,1),(150,.5), and(180,0). The quadratic curve fit to the sine was quad_sine = -0.00012094*x^2 +0.02176871*x -0.01360544, condition that 0<+A1<180 degrees. Another least squares fit was tried with points (0,0)(30,.5)(45,0.7071067811865476) and (90,1). The quadratic curve fit to the sine was = -9.84020089e-05*x^2 +2.00021484e-02*x -2.09138902e-03, condition that 0<+x<90 degrees. The quadratic formula for +x<90 was loaded into a TCL procedure and returned an error of 2 percent from the sine. Lets develop and model an error curve by spreadsheet sine minus quadratic formula. The error curve was modeled by another quadratic as error = 1.39361485e-05*x^2 -6.99389504e-04*x -1.15936030e-02. The sum of the quadratic fit and error fit curves was slightly better in tracking the spreadsheet sine, up to the limit or turning point of 90 degrees.
Taking a clue from Bhaskara, other fits to the sine curve can be tried from an online curve fitter, using the least squares method. The cubic equation was sind = 1.077526*e^(-(x - 90)^2/(2*44.85532^2)), condition 0<x<180 degrees. A fifth degree polynomial from least squares was sind = 0.00003431266 + 0.01720044*x + 0.00001589327*x^2 - 0.000001238347*x^3 + 3.439853e-9*x^4 + 1.479442e-24*x^5 degrees, from 6 points and 0<x<180. A Gaussian bell curve was sind = 1.077526*e^(-(x - 90)^2/(2*44.85532^2)), where 0<x<180 and not a good fit to the eyeball. Somewhat closer fits to sine are found by limiting the interval from 0 to 90 degrees and not turning the corner. The linear fit or stick fit was sind = 0.01578989*x + 0.01203364 degrees, condition that 0<x<90. The linear slope can be defined from simple points such as .5/30 = 0.0166...666 or ((sqrt 2)/2)/45 = 0.0157... An exponential growth fit is sind = -0.04863185 - (-0.02464133/0.01849654)*(1 - e^(-0.01849654*x)).
Horses 1)quadratic and 2)exponential appear winners of field with more than 200 entries for sine fitting functions. The fitted points on the sine curve were 0<x<90 degrees and available to double precision, E-14. Some calculations appear defaulted to single precision, E-7. Tabled chi results from 208 equations of 2 parameters (2P) or 2 terms (t2), from the non-linear curve fit algorithm (NLCF). Undoubtly, this would be hundreds of man-hours in paper calculations, but done automatically on the computer in three seconds or less. As might be expected, the sine, cosine, and tangent functions appear with high on the computed CHI scores, but analysis is looking for functions comparable to Taylor series and independent of trig functions, not snake eating tail. Trig functions are trivial results in this search, but leaving available in table, in case trig results jog memory.
For inclusion in the horse race of sine fitting formulas, the classic sigmoidal functions were estimated like the Richards growth curve, Weibull growth curve, Gaussian growth curve, and Gompertz growth curve, but sigmoidal chi scores were not stressing the pack. In these growth functions, the Levenberg-Marquardt (L-M) algorithm was used with double precision C's. These sigmoidal formulas were loaded into TCL procs.
#Normalized trig equations. The simplest quadratic match was sind = A*X+B*X**2, solving above for 0<+X<180. However, the autosolve can also solve (A*X+B*X**2) for the angle normalized to one, as condition for 0<+X<1.0. As graphed below, the normalized solution was sin_n = 1.763*X-0.7218*X**2. The normalized sine curve has the break points of (0,0),(.5,1),and (1,0) which generate three equations, <+c=0,0.25a+0.5b+c=1,a+b+c=0 # norm. sin> which can solved as 4*x-4*x**2 , 4*(x-x**2), or 4*x*(1-x). The normalized cosine curve has the break points of (-.5,0),(0,1),and (.5,0) which generate three equations, < 0.25a-0.5b+c=0,+c=1,0.25a+0.5b+c=0 #norm. cos > which can solved as 1-4*x**2. The normalized tangent curve has the break points of (-.5,-1),(0,0),and (.5,1) which generate three equations <0.25a-0.5b+c=0,+c=0,0.25a+0.5b+c=1 #norm. tan> which can solved as +2*x. The curve y= (1-A*(x-1)**2) is reasonable fit to the normalized sine. The average error on residuals to the normalized sine was -9.58E-03 or roughly ABS(.01). The curve y= (1-x**2) is reasonable fit to the normalized cosine. The average error on residuals to the normalized cosine was -6.68E-03 or roughly ABS(.01). The critical point in Bhaskara's sine derivation (read genius here!) was (30 degrees,0.5 sine), which is ((1/3)*(1/2),0.5) on the normalized sine curve. The additional and fourth equation was .0277777a+.16666666b+c =.5 or ((1/6)**2)*a+ (1/6)*b+c =(1/2). Loading the equivalent fourth equation with the previous solution, the Wolfram alpha solver reported solution as (19/5)* .
The paper of Karel Stroethoff averages a correcting polynomial to the Bhaskara sine with results accurate to 4 decimal points. Average means ((formula(40500) plus correcting poly))/2. The extended Bhaskara_Stroethoff sine was (2*aa*(180-aa))/(40500-aa*(180-aa))+(31*aa*(180-aa))/648000 + (aa*aa*((180-aa)**2))/583200000. The relative error on the Bhaskara_Stroethoff sine was 0.0366 percent versus the relative error of 0.173 percent on the original formula(cc=40500). The bhaskara_stroethoff sine gave about 0.173/0.0366 or 4.7 times improvement. Using the original formula and cos(phi)= sin (aa+90), the Stroethoff paper derived a cosine formula (32400-4*aa*aa)/(2*(32400+aa*aa))+(27900*(90*90-aa)+(90*90-aa*aa)*(90*90-aa*aa))/(2*291600000), (Blaskara cosine and correcting polynomial function)/2. The relative error on the Bhaskara_Stroethoff cosine was about 0.099 percent.
Various curve fits for the tangent can be evaluated over the interval from 0 < aa < pi/4 and compared to the spreadsheet tangent. The first curve was a linear fit as Y=aa*slope or Y = aa* (1/45) degrees. The linear fit for small angles less than 15 degrees is fairly good and has been used in numerous astronomy papers. At small angle, the sine curve is very close to the tangent and the second order sine multiplied by 2/(sqrt 2) to fit the tangent exactly at pi/4 is fairly close to the spreadsheet tangent. However, the tangent curve is steeper than the second order sine. Given the first two terms for taylor series of tangent (x+(1/3)x**3), a second order sine expression like the Bhaskara_sine would not match the steepness of the true tangent. The Bhaskara sine formula (cc=40500) times 2/(sqrt 2) is fairly close to the tangent and was found to have a relative error of 0.17 percent over the interval of interest, 0 < aa < pi/4 . Adapting the Stroethoff formula for the tangent, the Stroethoff_tangent is (2/(sqrt 2)*27900*aa*(180-aa)+aa*aa*(180-aa)*(180-aa)/291600000.
Console program for Bhaskara sine function
The console program below contains an angle wrap reduction procedure in degree measures for the Blaskara sine. Several dusty C++ posts have mentioned a large angle wrap error in C++ versions of angle reduction schemes, for angles of 1.E22 radians. Another post cited angle wrap reduction for trig functions as a non-trivial and unsung problem (probably in round-off error on floating points). This style error can be duplicated in the TCL proc with an input large angle and an input angle error, counting an initial error as 1E-13 and loading large angles as proc(1.0000000000001E5 degrees) returning 280.00000000999, proc(1.0...1E10 degrees) returning 280.000999, and 1.0...1E12 returning 280.0999 . The wish85 window delays returning console after loading greater magnitude angles, but the error growth will sink useful answers after inputs over 1E15 degrees.
The trial error for the console program below for pi/4 or 45 degrees was expr (0.707106-.705882)/.705882 = 0.001734 or 0.17 percent. For angles greater than -+360 degrees, an angle reduction procedure was added to evaluate only angles less than 360 degrees magnitude. The validity for the original Blaskara sine formula was positive angle in the interval from zero to 180 degrees. Blaskara was very careful in selecting his interval of validity; the published Blaskara sine table was from zero to 90 degrees. One good feature of the Bhaskara sine is that the Blaskara sine by itself is roughly accurate short of the interval end at 180 degrees or pi limit, unlike the Taylor and Pade sines which fail much beyond pi/4. For example in testcase 4, the Bhaskara sine evals 179 degrees with relative accuracy of 0.017 or 1.7 percent. Some of the other B_trig functions begin to fail after pi/4, so the valid region for each B_trig function has to be carefully checked. Extending the Bhaskara sine into other N*180 regions is possible with fold and multiply -1. statements. Additional significant figures are used to check the TCL console program, not to infer the accuracy of inputs and product reports.
Blaskara sine formula versions, 13 centuries of Indian mathematics and astronomy
| Blaskara sine formula versions, 13 centuries of Indian mathematics and astronomy | printed in TCL/WIKI format | ||
|---|---|---|---|
| formula version | date CE | source | comment |
| sin aa = ( 4*aa*(180-aa))/(40500-aa*(180-aa)) degrees | 600 | Mahdbhdskaflya of Bhaskara I | |
| R*sin aa=( R*aa*(180-aa))/(10125-(1/4)*aa*(180-aa)) | 628 | Siddhata | |
| sin aa = (aa*(180-aa)*4)/(40500-aa*(180-aa)) | 904 | Vatesvara-siddhanta | |
| sin aa = (aa*(180-aa*aa))/(10125-(1/4)*(aa*180-aa*aa)) | 904 | Vatesvara-siddhanta | taking angle square |
| sin aa = (aa*(180-aa*aa))/(40500-aa*(180-aa*aa)) | 1039 | Brahmagupta's (598 – 668 CE) Brhma-Sphuta-Siddhanta | taking angle square |
| 2*R*sin aa=(2 *R*(180*180-(180-2*aa)**2)/((1/4)*(360*360+(180-2*aa)**2)) | 1150 | Bhaskara II (1114 – 1185 CE) Lilavati | taking angle square |
| 2*R*sin aa=(2 *R*(360-2*aa)*2*aa)/((40500-aa*(180-aa)) | 1356 | Ganita Bharati | |
| sin aa =( 4*aa*(180-aa))/((40320-aa*(180-aa)) | 1520 | sanati | used different constant |
| cos aa =( 4*(90+aa)*(90-aa))/(40500-(90+aa)*(90-aa)) | 1910 | shulka, publshed 1910 in west | modern derivation from shifting phi= 90-aa |
| cos aa = (4*(8100-aa*aa))/(32400+aa*aa) | 1915 | lucknow edition | modern derivation from shifting phi= 90-aa |
| sin aa =( 4*aa*(180-aa))/(40500-aa*(180-aa)) | 1967 | Gupta using c.f.., Thiele originated | modern derivation continued fractions |
| sin aa = (4*P)/(5-P) where P=aa*(180-aa)/8100 | 1967 | Gupta, from linear rule | modern derivation from linear rule and substitution |
| sin aa = (4*P)/(5-P) where P=phi*(2-phi) and phi in quadrants (90 deg) | 1967 | Gupta, from linear rule | believed close to original Bhaskara (1&2) derivation from linear rule and substitution |
| Bhaskara 1 called his rule the source of direct and indirect (inverse) sines | implying that his formula could produce the inverse sine as well. |
Sine Fitting functions Rated by CHI scores
| Sine Fitting functions Rated by CHI scores | in TCL wiki format | printed in TCL wiki format | ||||
|---|---|---|---|---|---|---|
| f(x) slang name | formula | f(x) comp no. | Red. Chisq. | comment. if any | ||
| 1 | sine, might expect | Y=A*SIN(B*X) | 61 | 5.33152e-016 | sine f(x), might expect No. 1, A=0.100000E+01 ,B=0.174533E-01 | |
| 2 | quadratic | Y=A*X+B*X**2 | 24 | 5.88382e-006 | A=0.181886E-01, B=-.539003E-04 | |
| 3 | exponential | Y=A*(1-EXP(B*X)) | 58 | 7.74694e-006 | A=0.271990E+01 , B=-.672045E-02 | |
| 4 | linear fit,stick fit | Y=A*X+B | 6 | 0.000163659 | A=0.157899E-01, B=0.120337E-01 | |
| 5 | inverted parabolic | Y=A/X**2 | 2 | 0.000197795 | A=0.161473E-01 | |
| 6 | tangent, might expect | Y=A*TAN(B*X) | 63 | 0.00162301 | A=0.177184E+01, B=0.925430E-02 | |
| 7 | near quadratic, t2 | Y=A*X**2+B | 7 | 0.00751673 | A=0.324470E-03, B=0.116307E+00 | |
| 8 | cosh, hyperbolic | Y=A*COSH(B*X) | 151 | 0.0122198 | A=0.155194E+00 , B=0.509858E-01 | |
| 9 | sinh, hyperbolic | Y=A*SINH(B*X) | 150 | 0.0137778 | A=-.147058E+01 , B=-.835068E-02 | |
| 10 | parabolic | Y=A*X**2 | 3 | 0.0145212 | A=-.147058E+01 , B=-.835068E-02 | |
| 11 | fixed constant | Y=A | 1 | 0.0764166 | A=0.350388E+00 | |
| 12 | cosine, might expect | Y=A*COS(B*X) | 59 | 0.243049 | A=0.166935E+00 ,B=0.384725E-01 | |
| 13 | bhaskara sine formula | A + ( 4*x*(180-x))/(40500-x*(180-x)) | 1.15000E-06 | L-M, A = 0.65887563862E-04, stats seem wrong, check? | ||
| 14 | Richards growth function | Y = 1/(A+B*EXP(C*X))**D+E | 29.2152E-06 | L-M, solved for double precision constants | ||
| 15 | Gompertz growth function | Y = A*EXP(B*EXP(C*X))+D | 80.8294E-06 | L-M, solved for double precision constants | ||
| 16 | Gaussian growth function, bell curve | Y = A*EXP(((X-B)**2)/C)+D | 3.76536E-06 | L-M, solved for double precision constants |
| notes | chi results from 208 equations of 2P or 2t | trig functions are trivial results, but leaving, in case memory jog | ||||
| notes | calcs are either single precision, E-7 or solved for double precision, E-14 | horses 1)quadratic and 2)exponential appear winners of field with 208 entries | ||||
| Data fitted | X Axis Degrees | Y Axis sine | ||||
| 1 | 0 | 0 | ||||
| 2 | 5 | 0.08715574274766 | ||||
| 3 | 10 | 0.17364817766693 | ||||
| 4 | 20 | 0.34202014332567 | ||||
| 5 | 30 | 0.5 | ||||
| 6 | 40 | 0.64278760968654 | ||||
| 7 | 45 | 0.70710678118655 | ||||
| 8 | 50 | 0.76604444311898 | ||||
| 9 | 60 | 0.86602540378444 | ||||
| 10 | 70 | 0.93969262078591 | ||||
| 11 | 80 | 0.98480775301221 | ||||
| 12 | 90 | 1 | ||||
| 13, stop > 90 | 100 | 0.98480775301221 | ||||
| 14 | 110 | 0.93969262078591 | ||||
| 15 | 120 | 0.86602540378444 | ||||
| 16 | 130 | 0.76604444311898 | ||||
| 17 | 140 | 0.64278760968654 | ||||
| 18 | 150 | 0.5 | ||||
| 19 | 160 | 0.34202014332567 | ||||
| 20 | 170 | 0.17364817766693 | ||||
| 21 | 180 | 0 |
Screenshots Section
figure 1. Original Bhaskara Sine with 40500 constant
figure 2. Error of Bhaskara Sine with 40500 constant
figure 3. Bhaskar_Stroethoff Sine with corrective poly
figure 4. Error of Bhaskar_Stroethoff Sine with corrective poly
figure 5. Error of Bhaskara Sine with 40320 constant
figure 6. Bhaskara_Stroethoff Cosine
figure 7. Bhaskara_Stroethoff Cosine Error
figure 8. Spreadsheet tangent
figure 9. Curve fits to spreadsheet tangent
figure 10. Quadratic Curve fits to spreadsheet sine
figure 11. Quadratic Curve fits to spreadsheet cosine
figure 12. Quadratic Curve fit plus error curve, slightly better fit
figure 13. Richards growth function converged to sine
figure 14. Richards growth function, plotted residuals
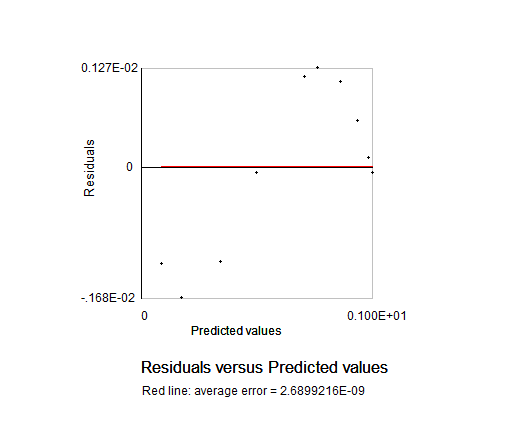
figure 15. Gompertz growth function fitted to sine
figure 16. Weibull growth function fitted to sine
figure 17. Gaussian growth function fitted to sine
figure 18. Bhaskara cosine formula normalized to one
figure 19. Simplest quadratic fit to sine, normalized to one
figure 20. Fit to normalized sine curve
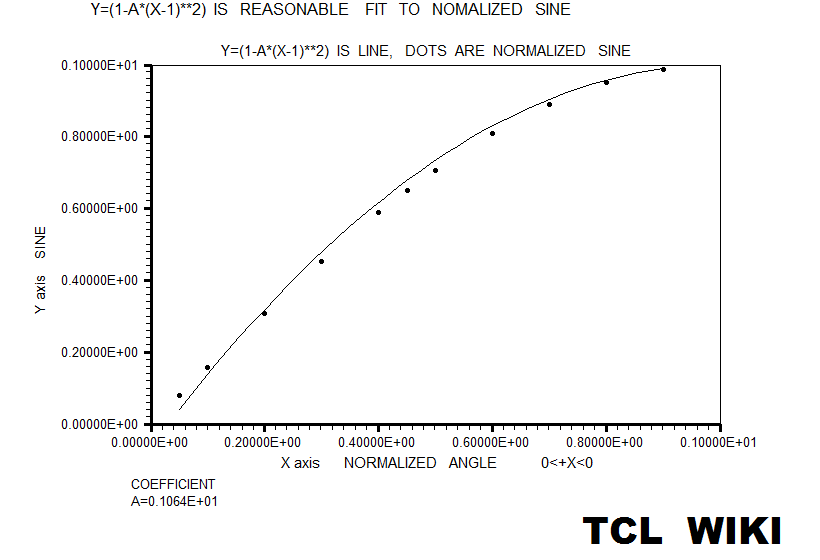
figure 21. Residuals from fit to normalized sine
figure 22. Fit to normalized cosine
figure 23. Residuals from fit to normalized cosine
figure 24. Wolfram solution to normalized sin
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console.
Testcase 1
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 765 original_angle_side1 : | degrees | original angle reduced for computation |
| 45.0 : | degrees | entry angle after reduction |
| 0.017453292519943 : | answers : conv. to radians | |
| 0.7058823529411765 : | cosd function | math.h derived cosd 0.7071067811865569 |
| 1.0 : | tand function | math.h derived tand 0.9999999999999735 |
| 1.0 : | cotd function | |
| 1.4166666666666667 : | secd function | |
| 1.4166666666666667 : | cscd function | |
| 0.7058823529411765 : | sind function | math.h derived cosd 0.7071067811865569 |
Testcase 2
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 60 original_angle_side1 : | degrees | original angle reduced for computation |
| 60 : | degrees | entry angle after reduction |
| 0.017453292519943 : | answers : conv. radians, used in arc functions | |
| 0.5 : | cosd function | comparison math.h derived cosd 0.5000000000000153 |
| 1.7297297297297298 : | tand function | comparison math.h derived 1.7320508075688066 |
| 0.578125 : | cotd function | |
| 2.0 : | secd function | |
| 1.15625 : | cscd function | |
| 0.8648648648648649 : | sind function | comparison math.h sind 0.8660254037844298 |
Testcase 3
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 20 original_angle_side1 : | degrees | original angle reduced for computation |
| 20 : | degrees | entry angle after reduction |
| 0.017453292519943 : | answers : conv. radians, used in arc functions | |
| 0.9390243902439024 : | cosd function | comparison math.h derived cosd 0.9396926207859104 |
| 0.3654468855541242 : | tand function | comparison math.h derived tand 0.3639702342661957 |
| 2.736375762195122 : | cotd function | |
| 1.0649350649350648 : | secd function | |
| 2.9140625 : | cscd function | |
| 0.34316353887399464 : | sind function | comparison math.h derived sind 0.34202014332566316 |
Testcase 4
| table 4 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 4: | testcase_number | |
| 179. original_angle_side1 : | degrees | original angle reduced for computation |
| 179. : | degrees | entry angle after reduction |
| 0.017453292519943 : | answers : conv. to radians | |
| -1.4860725314628884 : | cosd function | |
| -0.011949279539112682 : | tand function | |
| -83.68705382837308 : | cotd function | |
| -0.6729146652186625 : | secd function | |
| 56.314245810055866 : | cscd function | |
| 0.01775749609384688 : | sind function |
bhaskara_sinx 179. 0.01775749609384688 179 deg comparison tcl derived
cosd -0.9998476951563903 sind 0.017452406437336275 tand -0.01745506492827037 atan 1.261013419037191
References:
- search keywords for "faster" trig approximations.
- sin cos tan trig series efficient approximation "nested polynomial" multiplication
- "Horner's method" "Horner's form" recursive telescoping
- The Bhaskara-Aryabhata Approximation to the Sine Function,
- Author(s): Dr. Shailesh A. Shirali, Source: Mathematics Magazine,
- Vol. 84, No. 2 (April 2011), pp. 98-107
- Payne, Mary H.; Hanek, Robert N., Radian reduction for Large Angles,
- implemented on Sparc 3, probably C++ code and bit instructions
- Argument reduction for huge arguments: Good to the Last Bit,
- K. C. Ng, SunPro Works , March 24, 1992
- High Precision Calculation of Arcsin x, Arceos x, and Arctan
- By I. E. Perlin and J. R. Garrett, ie. polynomial approximation
- A Fast-Start Method for Computing the Inverse Tangent,
- Peter Markstein, Hewlett-Packard Laboratories
- Faster Math Functions, Robin Green , Sony Computer Entertainment America
- Bhaskara 1's approximation to sine, R.C. Gupta,1967
- very detailed on multiple versions of Bhaskara sine formula
- Wikipedia, Bhaskara I's sine approximation formula
- Bhaskara’s approximation for the Sine, Karel Stroethoff
Appendix Code
appendix TCL programs and scripts
console TCL script for Bhaskara sine formulas
# Indian math Bhaskara sine formula and extensions, History math
# pretty print from autoindent and ased editor
# Bhaskara sine formula and extensions into TCL
# written on Windows XP on TCL
# working under TCL version 8.5.6
# gold on TCL WIKI , 20dec2017
package require Tk
package require math::numtheory
package require math::geometry
package require math::constants
package require math::bigfloat
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::geometry math::constants math::bigfloat}
#namespace import ::math::bigfloat::*
set tclprecision 17
wm title . "Bhaskara sine formula and extensions into TCL"
console show
proc degree_reduction {aa} {
if { $aa > 360. } {
while {$aa > 360.} {
set aa [- $aa 360.] }
return $aa }
if { $aa < -360. } {
while {$aa < -360.} {
set aa [+ $aa 360.] }
return $aa }
return $aa }
proc reportx {} {
global bhaskara_sindx bhaskara_cosdx bhaskara_tandx x angle_keeper
global bhaskara_secdx bhaskara_cscdx bhaskara_cotandx reduced_angle
set testcase_number 1
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |&"
puts "&| $angle_keeper original_angle_side1 :|degrees | original angle reduced for computation |&"
puts "&| $reduced_angle :|degrees | entry angle after reduction |&"
puts "&| $math::constants::degtorad :|answers : conv. to radians | |& "
puts "&| $bhaskara_cosdx :|cosd function| |& " proc bhaskara_tandx {x} {
# probably use globals to fill out wiki table
global bhaskara_sindx bhaskara_cosdx bhaskara_tandx angle_keeper
global bhaskara_secdx bhaskara_cscdx bhaskara_cotandx reduced_angle
set angle_keeper $x
set reduced_angle [ degree_reduction $x ]
set x [ degree_reduction $x ]
# uncomment below to return to radian measure
#set x [* $x $math::constants::degtorad ];
# sind was -pi< x >pi,
# but other trig funcs were mostly positive x < pi/2
set pi $math::constants::pi
set bhaskara_sindx [ expr { (4.*$x*(180.-$x))/( 40500.-$x*(180.-$x)) } ]
set bhaskara_cosdx [ expr { ((4.*(90.-$x))*(90.+$x))/( 32400.+$x*$x) } ]
set bhaskara_tandx [ expr { $bhaskara_sindx/$bhaskara_cosdx } ]
set bhaskara_cotandx [ expr {$bhaskara_cosdx/$bhaskara_sindx } ]
set bhaskara_secdx [ expr { ( 32400.+$x*$x)/((4.*(90.-$x))*(90.+$x)) } ]
set bhaskara_cscdx [ expr { ( 40500.-$x*(180.-$x))/(4.*$x*(180.-$x)) } ]
set result $bhaskara_tandx
return $result }
puts "&| $bhaskara_tandx :|tand function| |&"
puts "&| $bhaskara_cotandx :|cotd function | |&"
puts "&| $bhaskara_secdx :|secd function | |&"
puts "&| $bhaskara_cscdx :|cscd function | |&"
puts "&| $bhaskara_sindx :|sind function | |&"
}
puts " bhaskara_tandx 765 [ bhaskara_tandx 360045.0000000000001 ] "
reportx
# output
# bhaskara_tandx 45 1.0 # folding statements for Bhaskara sine
#Extending the Bhaskara sine into other N*180 regions
#is possible with fold and multiply -1. statements ( slang fold and flip) .
# for 180 < $x < 360, fold to 0-180 degrees and multiply -1.
set bhaskara_sindx [ expr { (4.*$x*(180.-$x))/( 40461.287-$x*(180.-$x)) } ]
if { $x > 179.9999999 && $x < 359.9999999 } { set x [- $x 180. ]; set bhaskara_sindx [ expr { -1.*(4.*$x*(180.-$x))/( 40500.-$x*(180.-$x)) } ] }
if { $x > -360 && $x < -180.0000001 } { set x [+ $x 360. ]; set bhaskara_sindx [ expr { +1.*(4.*$x*(180.-$x))/( 40500.-$x*(180.-$x)) } ] }
if { $x > -180 && $x < -0.0000001} { set x [+ $x 180. ]; set bhaskara_sindx [ expr { -1.*(4.*$x*(180.-$x))/( 40500.-$x*(180.-$x)) } ] }Extending the Bhaskara sine formula
# bhaskara_stroethoff_sine, corrected bhaskara sine with polynomial
# sine limits are 0 <aa <pi
proc bhaskara_stroethoff_sine {aa} {
set bhaskara_stroethoff_sine [ expr { (2.*$aa*(180.-$aa))/(40500.-$aa*(180.-$aa))+(31.*$aa*(180.-$aa))/648000 + ($aa*$aa*((180.-$aa)**2))/583200000. }]
set result $bhaskara_stroethoff_sine
return $result }
# cosine limits are 0 <aa <pi/2
proc bhaskara_stroethoff_cosine {aa}
set bhaskara_stroethoff_cosine [ expr { (32400.-4.*$aa*$aa)/(2.*(32400.+$aa*$aa))+(27900.*(90.*90.-$aa*$aa)+(90.*90.-$aa*$aa)*(90.*90.-$aa*$aa))/(2.*291600000.) }]
set result $bhaskara_stroethoff_cosine
return $result }
# changed constant, still limits of 0>aa<180
proc bhaskara_stroethoff_sine_c_40417 {aa}
set bhaskara_sind_ext [ expr { (4.*$x*(180.-$x))/( 40417.-$x*(180.-$x)) } ]
set result $bhaskara_sind_ext
return $result }
Bhaskara quadrant switch
# Bhaskara quadrant switch
# pretty print from autoindent and ased editor
# Bhaskara sine formula and extensions into TCL
# written on Windows XP on TCL
# working under TCL version 8.5.6
# gold on TCL WIKI , 20dec2017
package require Tk
package require math::numtheory
package require math::geometry
package require math::constants
package require math::bigfloat
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::geometry math::constants math::bigfloat}
#namespace import ::math::bigfloat::*
set tclprecision 17
wm title . "Bhaskara quadrant switch "
console show
if {0} {
set pi $math::constants::pi
set bhaskara_sindx [ expr { (4.*$x*(180.-$x))/( 40320.-$x*(180.-$x)) } ]
if { $x > 179.9999999 && $x < 359.9999999 } { set x [- $x 180. ]; set bhaskara_sindx [ expr { -1.*(4.*$x*(180.-$x))/( 40500.-$x*(180.-$x)) } ] }
if { $x > -360 && $x < -180.0000001 } { set x [+ $x 360. ]; set bhaskara_sindx [ expr { +1.*(4.*$x*(180.-$x))/( 40500.-$x*(180.-$x)) } ] }
if { $x > -180 && $x < -0.0000001} { set x [+ $x 180. ]; set bhaskara_sindx [ expr { -1.*(4.*$x*(180.-$x))/( 40500.-$x*(180.-$x)) } ] }
}
#proc errorx always returns a positive error.
#Normally assume $aa is human estimate,
#assume $bb is divinely exact.
proc errorx {aa bb} {expr { $aa > $bb ? (($aa*1.)/$bb -1.)*100. : (($bb*1.)/$aa -1.)*100.}}
#
proc sinl { aa } {
# switch for -360 < aa < 360
# 4 cases of 180 degrees each
set quadrant 1
set quadrant [+ [int [/ $aa 180.] ] 1]
# puts dropped for timing checks
# puts " $aa $quadrant "
if { $aa < 0 } { set quadrant [+ [int [/ $aa 180.] ] 4 ]}
# puts dropped for timing checks
# puts " $aa $quadrant "
set quadrant 0x$quadrant
set x $aa
set sinl 1
set number 0x5
#switch -- [format %d $quadrant]
switch -exact [format %d $quadrant] {
1 {set sinl [ expr { +1.*(4.*$x*(180.-$x))/( 40500.-$x*(180.-$x)) } ]}
2 {set x [- $x 180. ]; set sinl [ expr { -1.*(4.*$x*(180.-$x))/( 40320.-$x*(180.-$x)) } ]}
3 {set x [+ $x 360. ];set sinl [ expr { +1.*(4.*$x*(180.-$x))/( 40500.-$x*(180.-$x)) } ]}
4 {set x [+ $x 180. ];set sinl [ expr { -1.*(4.*$x*(180.-$x))/( 40500.-$x*(180.-$x)) } ]}
default {return "default = unknown error out of bins"}
}
return $sinl}
set count -350
set aa -350
while {$aa < 340.} {
set aa $count
set x [* $aa $math::constants::degtorad ]
puts " homebrew sinl $aa [ sinl $aa ] comparison tcl derived sind [sin $x ] error [ errorx [ sinl $aa ] [sin $x ] ] ";
incr count 30 }
# testing switch TCL switch proc
set $aa 45.
set x [* $aa $math::constants::degtorad ]
puts " homebrew sinl 45 [ sinl $aa ] comparison tcl derived sind [sin $x ] "
puts " timing quadrant 1 time is [ time { sinl $aa } 10 ] "
puts " timing TCL_sin time is [ time { sin $x } 10 ] "
puts " timing quadrant 1 time is [ time { sinl $aa } 10 ] "
puts " timing TCL_sin time is [ time { sin $x } 10 ] "
proc time_tester {tt} {
set result ""
set number 0x5
switch -- [format %d $number] {
5 {set result "switch works " }
default {set result " switch unknown, default = unknown error out of bins"}
}
return $result}
puts " [ time_tester 1 ] "
puts " timing time_tester 1 [ time_tester 1 ] time is [ time { time_tester 1 } 100 ] "
# The Bhaskara trig functions have optimum accuracy between origin and pi/4.
# The Bhaskara trig functions continue to degrade after pi/4. The folding into
# quadrants of 90 degrees or sectors of 180 degrees help correct the
# functions, but do not eliminate the trend past pi/4. output
homebrew sinl -350 0.17525773195876287 comparison tcl derived sind 0.17364817766703186 error 0.9269053746232325
homebrew sinl -320 0.6418338108882522 comparison tcl derived sind 0.6427876096866116 error 0.1486052592086784
homebrew sinl -290 0.9390243902439024 comparison tcl derived sind 0.9396926207859377 error 0.07116221356739949
homebrew sinl -260 0.9846153846153847 comparison tcl derived sind 0.9848077530121948 error 0.019537415301029704
homebrew sinl -230 0.7647058823529411 comparison tcl derived sind 0.7660444431189345 error 0.17504256170681742
homebrew sinl -200 0.34316353887399464 comparison tcl derived sind 0.34202014332561315 error 0.3343064935485307
homebrew sinl -170 -0.17525773195876287 comparison tcl derived sind -0.17364817766697968 error -0.9183927429586514
homebrew sinl -140 -0.6418338108882522 comparison tcl derived sind -0.6427876096865711 error -0.14838475165754872
homebrew sinl -110 -0.9390243902439024 comparison tcl derived sind -0.9396926207859195 error -0.07111160897042001
homebrew sinl -80 -0.9846153846153847 comparison tcl derived sind -0.9848077530122039 error -0.019533598941601227
homebrew sinl -50 -0.7647058823529411 comparison tcl derived sind -0.7660444431189686 error -0.17473669811864934
homebrew sinl -20 -0.34316353887399464 comparison tcl derived sind -0.34202014332566316 error -0.33319260900597225
homebrew sinl 10 0.17525773195876287 comparison tcl derived sind 0.17364817766692744 error 0.9269053746839173
homebrew sinl 40 0.6418338108882522 comparison tcl derived sind 0.6427876096865303 error 0.14860525919599965
homebrew sinl 70 0.9390243902439024 comparison tcl derived sind 0.9396926207859013 error 0.07116221356351371
homebrew sinl 100 0.9846153846153847 comparison tcl derived sind 0.9848077530122132 error 0.01953741530289488
homebrew sinl 130 0.7647058823529411 comparison tcl derived sind 0.7660444431190025 error 0.1750425617157214
homebrew sinl 160 0.34316353887399464 comparison tcl derived sind 0.3420201433257131 error 0.3343064935191986
homebrew sinl 190 -0.17607457276022787 comparison tcl derived sind -0.17364817766687493 error -1.3780496839013279
homebrew sinl 220 -0.6451612903225806 comparison tcl derived sind -0.6427876096864896 error -0.3679204985941098
homebrew sinl 250 -0.944206008583691 comparison tcl derived sind -0.9396926207858832 error -0.47800879858600487
homebrew sinl 280 -0.9900990099009901 comparison tcl derived sind -0.9848077530122225 error -0.5344169457655368
homebrew sinl 310 -0.768775872264932 comparison tcl derived sind -0.766044443119037 error -0.35529589890066493
homebrew sinl 340 -0.3448275862068966 comparison tcl derived sind -0.3420201433257629 error -0.8141584355287557
homebrew sinl 45 -0.3448275862068966 comparison tcl derived sind -0.3420201433257629
timing quadrant 1 time is 21.5 microseconds per iteration
timing TCL_sin time is 2.7 microseconds per iteration
quadrant 1 time is 20.6 microseconds per iteration
TCL_sin time is 2.8 microseconds per iteration
switch works
timing time_tester 1 switch works time is 3.98 microseconds per iteration # test code for very rough tangent
# based on early statement derivations
# early base of Bhaskara derivations
proc tanm {x} {
set tanm [ expr { ($x*(180.-$x))/((90.-$x)*(90.+$x)) }]
return $tanm
}
# tanm 45. 1.0
# tanm 30. 0.625 , should be (sqrt 3) /3, error 8 percent
proc sin_angle_reduction {aa } {set pi [ expr { acos(-1) } ]; expr {abs($aa)>360? asin ( sin($aa*($pi/180.)) ) * (180./$pi) : $aa } }
puts " sin angle reduction [ sin_angle_reduction 30. ] "
puts " sin angle reduction [ sin_angle_reduction 760. ] "
puts " sin angle reduction [ sin_angle_reduction -760. ] "
puts " timing sin angle reduction [ time {sin_angle_reduction -760. } 100 ] "
puts " timing degree_reduction [ degree_reduction 900005.0000000000001 ] "
puts " timing degree_reduction [ time {degree_reduction 900055.0000000000001 } 100 ] "
# sin angle reduction 30.0
#sin angle reduction 40.00000000000003
#sin angle reduction -40.00000000000003
#timing sin angle reduction 5.7 microseconds per iteration
#timing degree_reduction 4.98 microseconds per iteration
Classic sigmoidal functions in TCL script
proc sindgaussian {x} {
# fit gaussian growth curve to sine
# condition 0<+x<90
#set x [* $x $math::constants::degtorad ];
set A 0.27601397923E+01
set B 0.89847055041E+02
set C -0.17926590835E+05
set D -0.17602884876E+01
set x [ expr { $A*exp((($x-$B)**2)/$C)+$D }]
return $x}
proc sindrichards {x} {
# fit richards growth curve to sine
# condition 0<+x<90
#set x [* $x $math::constants::degtorad ];
set A 0.48154253688E-07
set B 0.10525783963E-05
set C -0.59573538036E-01
set D 0.87125623376E-01
set E -0.32971579577E+01
set x [ expr { 1./($A+$B*exp($C*$x))**$D+$E }]
return $x}
proc sindgompertz {x} {
# fit gompertz growth curve to sine
# "double exponential fits most anything"
# condition 0<+x<90
#set x [* $x $math::constants::degtorad ];
set A 0.12218253807E+01
set B -0.20592195352E+01
set C -0.38221525189E-01
set D -0.13115026413E+00
set x [ expr { $A*exp($B*exp($C*$x))+$D }]
return $x}
puts " sindgaussian 30 [ sindgaussian 30 ] "
puts " sindrichards 30 [ sindrichards 30 ] "
puts " sindgompertz 30 [ sindgompertz 30 ] "gold This page is copyrighted under the TCL/TK license terms, this license .
Comments Section
Please place any comments here, Thanks.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |