Version 1 of Kahan compensated summation algorithm and Neumaier variant summation algorithm, numerical analysis
Updated 2018-01-13 14:24:00 by goldGauss Approximate Number of Primes and eTCL demo example calculator, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER in your comment with the same courtesy that I will give you. Its very hard to reply intelligibly without some background of the correspondent. Thanks,gold
- Gauss Approximate Number of Primes and eTCL demo example calculator, numerical analysis
- Introduction
- Gauss and Legendre approximations
- devil's notch in Pcf(x)
- Appendix Code
- Comments Section
Introduction
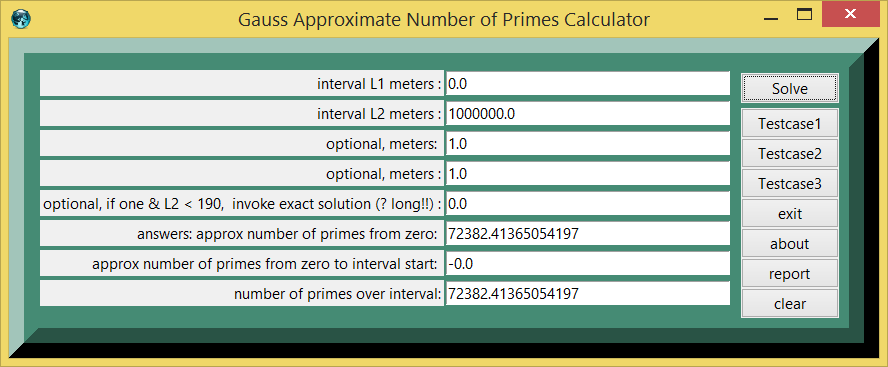
gold Here is some eTCL starter code for Gauss approximate number of primes. The impetus for these calculations was checking approximations for the Riemann theorem. Most of the testcases involve assumptions and rules of thumb.
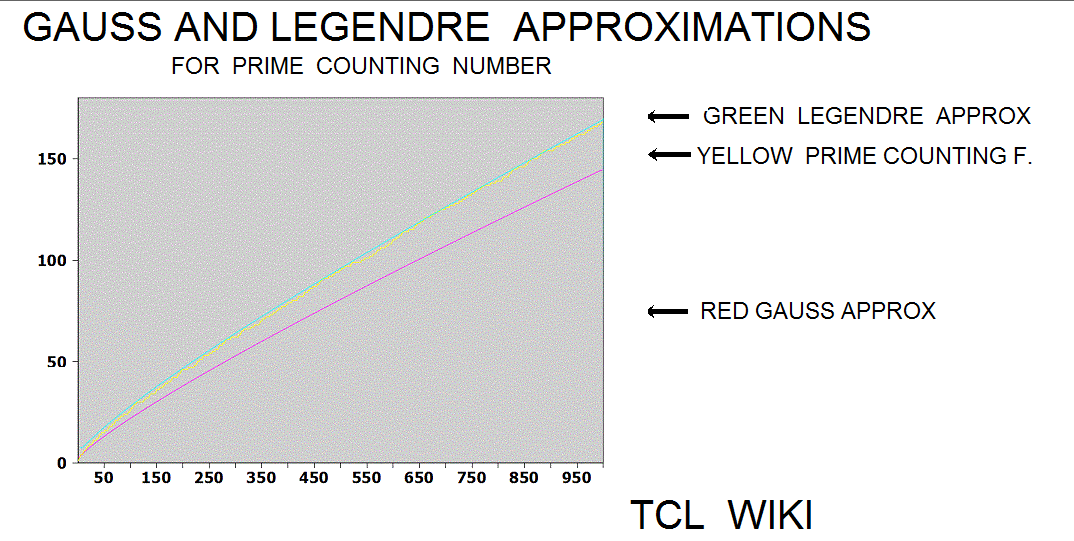
Gauss and Legendre approximations
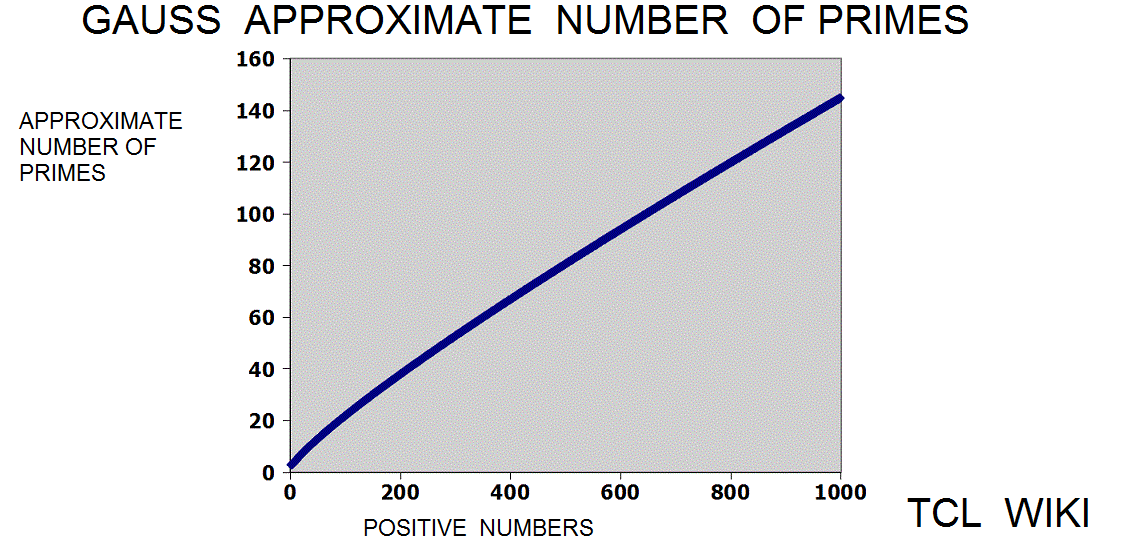
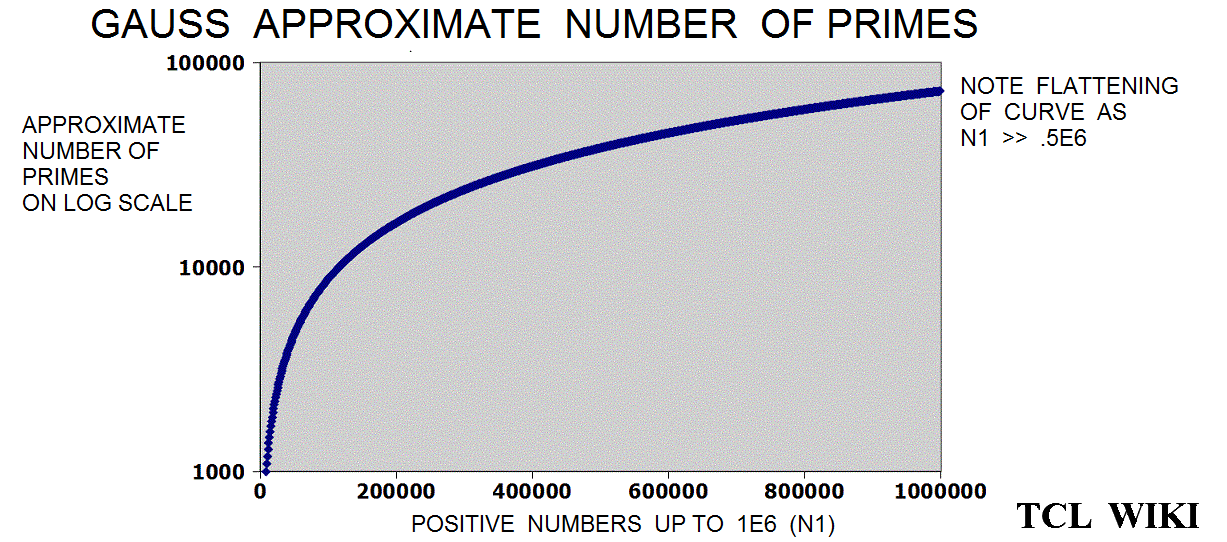
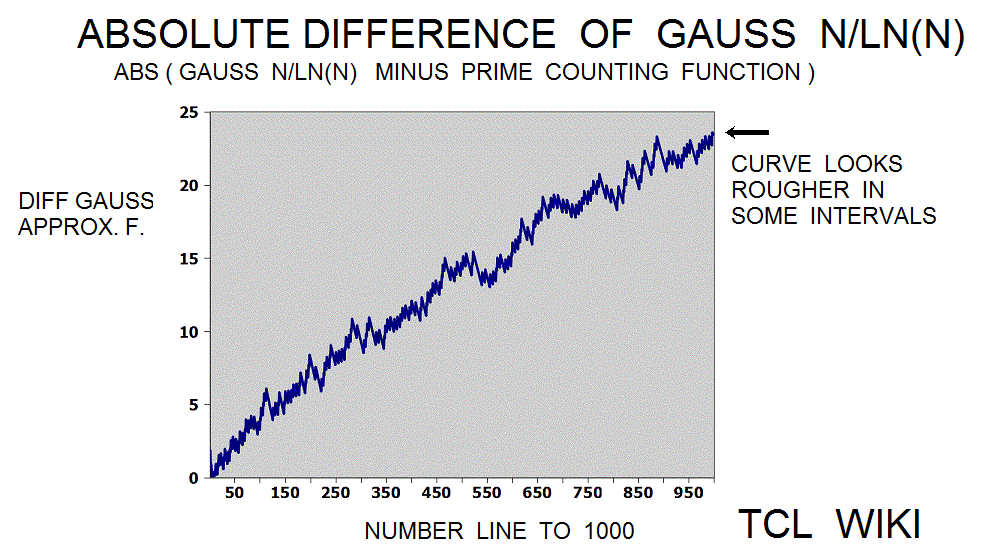
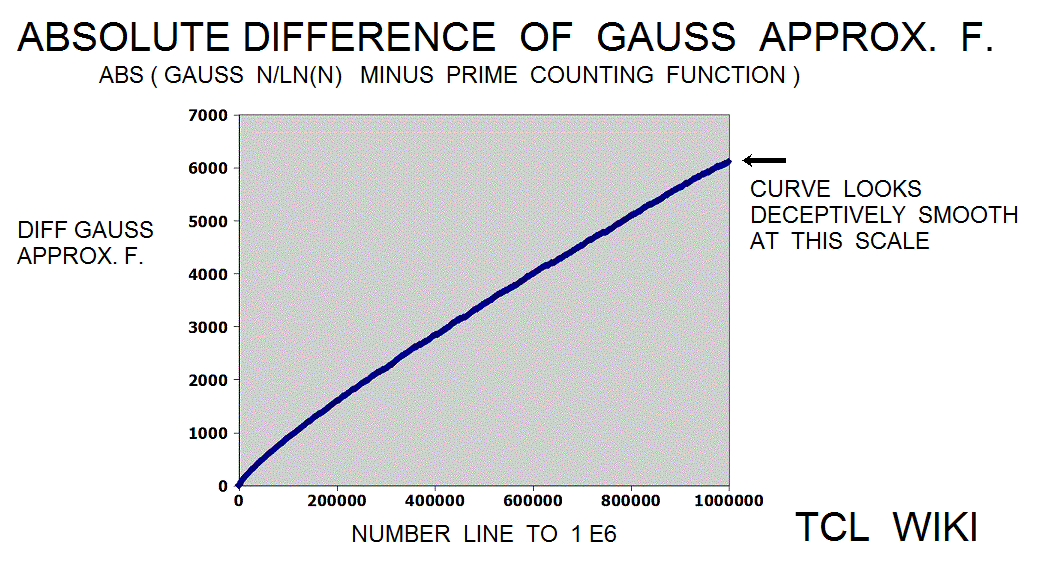
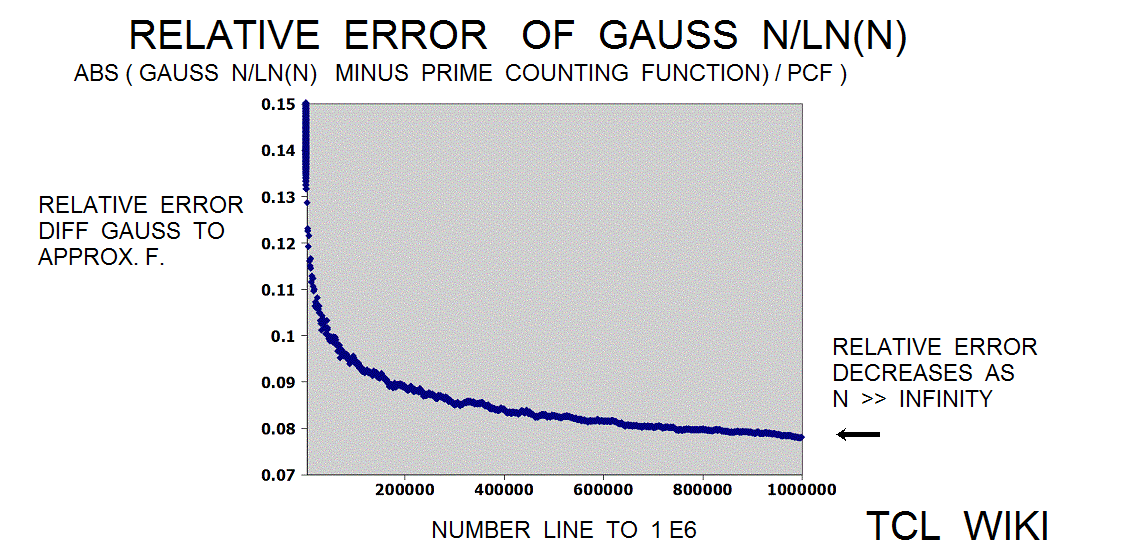
The Gauss approximation for number of primes is approx_number_primes = N1 / ln (N1), 15 percent average error. Gauss developed this formula at the age of 14! and formula was first published in 1863. If the exact solution is tabbed as one, the program is storing the exact solution in a list of limited size. The number one should not be counted as a prime and the number two is counted as prime, so some starting algorithm statements are tricky.
The Legendre approximation for number of primes was approx_legendre_primes2 = N1 / (ln (N1)-1), 2 percent average error beyond 1E4. A variant of the Legendre equation was approx_legendre_primes3 = N1 / (ln (N1)-1.08366).
# following statements can be pasted into eTCL console set project 1.0 set approx_legendre_primes2 [/ 100. [- [log 100.] 1.] ] # answer 27.73794157864211 set approx_gauss_number_primes [/ 100. [log 100.] ] # answer 21.71472409516259
devil's notch in Pcf(x)
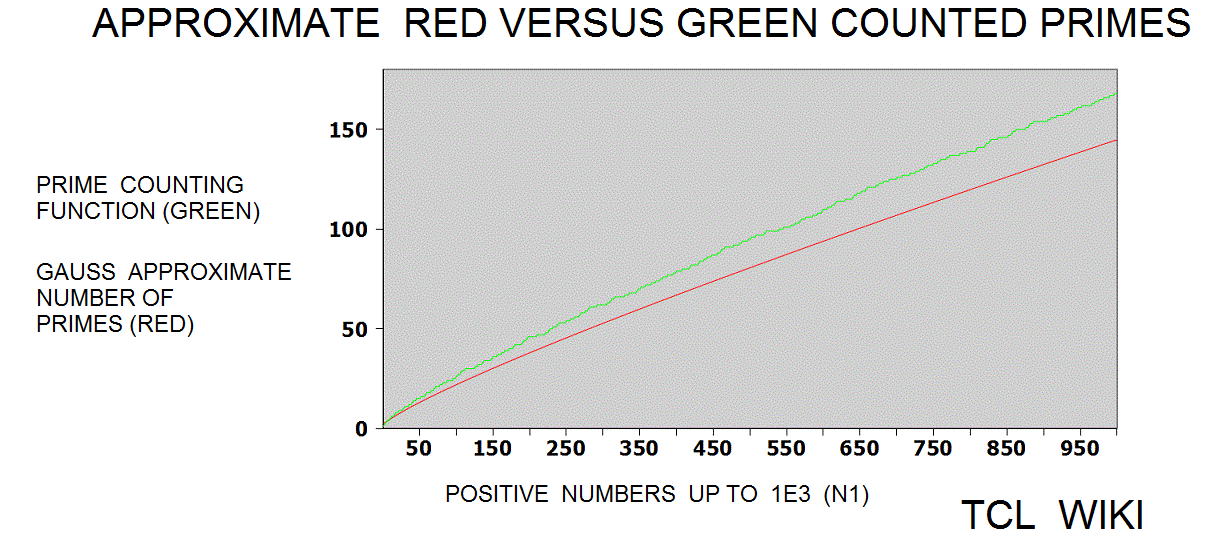
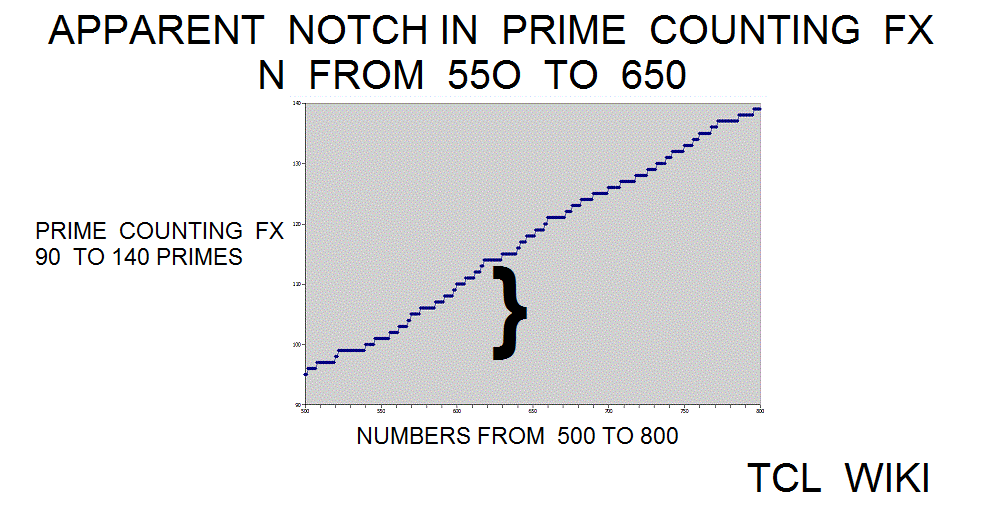
What causes the devil's notch in the prime counting function from numbers 550 to 650? This region is best seen on the graphs of the prime counting function or the difference curves between the prime counting function and the Gauss approximation. Maybe the notch is numerical coincidence in "random noise" or human misperception, but the notch can show some of the calculator uses. The calculator and some subroutines in the TCLLIB can be used to examine this region. Using the calculator in step intervals of (450 550), (550 650), and (550 650), there was a slight increase in the number of primes as steps 14,17,14. The gauss reported predictions of 13.505,13.191,12.936 primes in the notch and adjacent regions. The corrected legendre function reported predictions of 15.696,15.281,14.947 primes in the notch and adjacent regions. The slight increase in the devil's notch goes against the general trend that primes should become more rare either in the large numbers or as N increases. The corrected legendre function is one or two off in its prediction of prime numbers in the adjacent intervals, but the expectation from both the gauss and legendre functions is a gentle decrease in primes, not a bump up to 17 primes. As the calculator passes through the devil's notch, the prime numbers can be gathered in a list and printed out on the console. Try inserting lappend list and put statements in the TCLLIB::math::numtheory::prime_counting_functionx or the calculator . The prime number 601 is in the middle of the notch and its nearest integer root is 25, if a prime number has such baggage. Hinkley's Tables of primes has similar intervals of 100 mapped out, but no answer leaped from the pages.
Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
Testcase 1
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 1 | |
| 0.0 : | interval L1 meters | |
| 1000000.0 : | meters L2 meters | |
| 1.0 : | meters | |
| 1.0 : | meters | |
| 0.0 : | optional,if one, invoke exact solution (? long) | |
| 72382.41365054197 : | answers:approx_number_primes | |
| -0.0 : | approx_number_primes_interval_start | |
| 72382.41365054197 : | approx. number_primes_over_interval | |
| 78498: | exact solution from internet | |
| 8.4 : | error percent |
Testcase 2
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 2 | |
| 0.0 : | interval L1 meters | |
| 5.0 : | meters L2 meters | |
| 1.0 : | meters | |
| 1.0 : | meters | |
| 0.0 : | optional,if one, invoke exact solution (? long) | |
| 3.1066746727980594 : | answers:approx_number_primes | |
| -0.0 : | approx_number_primes_interval_start | |
| 3.1066746727980594 : | number_primes_over_interval | |
| 3.0 : | exact solution number_primes_over_interval | |
| 2.0 3.0 5.0 : | list number_primes_over_interval of 0 to 5 | |
| 0.55 : | error percent |
Testcase 3
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 3 | |
| 0.0 : | interval L1 meters | |
| 10.0 : | meters L2 meters | |
| 1.0 : | meters | |
| 1.0 : | meters | |
| 0.0 : | optional,if one, invoke exact solution (? long) | |
| 4.3429448190325175 : | answers:approx_number_primes meters | |
| -0.0 : | approx_number_primes_interval_start | |
| 4.3429448190325175 : | number_primes_over_interval | |
| 4.0 : | exact solution number_primes_over_interval | |
| 2.0 3.0 5.0 7.0 : | list number_primes_over_interval of 0 to 10 | |
| 8.5 : | error percent |
Testcase 4
| table 4 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 4 | |
| 0.0 : | interval L1 meters | |
| 100.0 : | meters L2 meters | |
| 1.0 : | meters | |
| 1.0 : | meters | |
| 1.0 : | optional,if one, invoke exact solution (? long) | |
| 21.71472409516259 : | answers:approx_number_primes meters | |
| -0.0 : | approx_number_primes_interval_start | |
| 25 : | exact solution number_primes_over_interval | |
| 2.0 3.0 5.0 7.0 11.0 13.0 17.0 19.0 23.0 29.0 31.0 37.0 41.0 43.0 47.0 53.0 59.0 61.0 67.0 71.0 73.0 79.0 83.0 89.0 97.0 : | list number_primes_over_interval | |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 | exact solution from internet | |
| 5.6 : | error percent |
Testcase 5
| table 5 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 5 | |
| 0.0 : | interval L1 meters | |
| 190.0 : | meters L2 meters | |
| 1.0 : | meters | |
| 1.0 : | meters | |
| 1.0 : | optional,if one, invoke exact solution (? long) | |
| 36.2110021579845 : | answers:approx_number_primes meters | |
| -0.0 : | approx_number_primes_interval_start | |
| 42 : | exact number_primes_over_interval meters | |
| 2.0 3.0 5.0 7.0 11.0 13.0 17.0 19.0 23.0 29.0 31.0 37.0 41.0 43.0 47.0 53.0 59.0 61.0 67.0 71.0 73.0 79.0 83.0 89.0 97.0 101.0 103.0 107.0 109.0 113.0 127.0 131.0 137.0 139.0 149.0 151.0 157.0 163.0 167.0 173.0 179.0 181.0 : | list number_primes_over_interval | |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181 | exact solution from internet |
| 15.9 : | error percent |
Testcase 6
| table 6 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 2 | |
| 0.0 : | interval L1 meters | |
| 1e+27 : | meters L2 meters | |
| 1.0 : | meters | |
| 1.0 : | meters | |
| 0.0 : | optional,if one, invoke exact solution (? long) | |
| 1.608498081123155e+25 : | answers:approx_number_primes | |
| -0.0 : | approx_number_primes_interval_start | |
| 1.608498081123155e+25 : | approx. number_primes_over_interval from 0 to 10E26 | |
| 1,699,246,750,872,437,141,327,603 28,883,358,936,853,188,823,261 155,891,678,121 58.850: | exact solution from internet | |
| 5.6 : | error percent |
Testcase 7 , devil's notch
| table 7 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 7 | |
| 550.0 : | interval L1 | devil's notch |
| 650.0 : | end number L2 | |
| 1.0 : | optional,if one, invoke exact solution (? long) | |
| 100.35553088418682 : | answers: gauss function ~number_primes | |
| 120.51962806243556 : | legendre function ~number_primes | |
| 100.35553088418682 : | gauss approx_number_primes | |
| 87.164361842509408 : | gauss approx_number_primes_interval_start | |
| 118 : | gauss number_primes_over_interval | |
| 120.51962806243556 : | legendre_function number_primes_N1 |
&| lister {557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647} :|exact solution from TCLLIB::math::numtheory]::prime_counting_functionx | |&
| 17 : | prime_counting_function over interval |
Screenshots Section
figure 1.
figure 2.
figure 3.
figure 4.
figure 5.
figure 6.
figure 7.
figure 8.
figure 9.
References:
- Primes
- Oneliner's Pie in the Sky
- One Liners
- TCLLIB ::math::numtheory]::prime_counting_functionx
- https://en.wikipedia.org/wiki/Prime-counting_function
- http://sweet.ua.pt/tos/primes.html#i
- http://mathworld.wolfram.com/PrimeCountingFunction.html
- http://www.math.uni-bonn.de/people/jbuethe/topics/AnalyticPiX.html
- http://primes.utm.edu/notes/rh.html
- http://numbers.computation.free.fr/Constants/Primes/pixtable.html
- http://numbers.computation.free.fr/Constants/constants.html
- on line prime number generator, see
- http://www.miniwebtool.com/list-of-prime-numbers/?to=50
- Mathematician pair find prime numbers aren't as random as thought, March 15, 2016 by Bob Yirka,
- ref Robert Lemke Oliver and Kannan Soundararajan, Stanford University
- google < Prime number theorem Wikipedia >
- Probability that a number is prime, John D. Cook, 6 October 2010
- Probability of Next Prime Digit, Kevin's Math Page, Kevin Gong,March 17th, 2016
- Mathematicians Discover Prime Conspiracy, Erica Klarreich , March 13, 2016, Quanta Magazine
- Prime Probability: Catch the Wave, Michael M. Ross , Excel spreadsheet, Jan2008
- Prime Numbers and Their Statistical Properties,Dr. Phillip M. Feldman
- 19TH CENTURY MATHEMATICS - GAUSS, The Story of Mathematics
- Dan Rockmore Stalking the Riemann Hypothesis, The Quest to Find the Hidden Law of Prime Numbers
Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# Gauss approximate number of primes calculator
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI, 15may2016
package require Tk
package require math::numtheory
#namespace path {math::numtheory}
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {interval number L1 :} }
lappend names {end number L2 :}
lappend names {optional, if one & L2 < 190, invoke exact solution (? long!!): }
lappend names {answers: gauss function ~number_primes for N1 :}
lappend names {legendre function ~number_primes for N1 :}
lappend names {gauss approx number of primes from zero: }
lappend names {gauss approx number of primes from zero to interval start: }
lappend names {gauss number of primes over interval:}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Gauss Approximate Number of Primes
from TCL WIKI,
written on eTCL "
tk_messageBox -title "About" -message $msg }
# ref. TCLLIB::math::numtheory::prime_counting_functionx
# ref. alternate TCLLIB::math::numtheory::isprime
proc prime_counting_function { start end } {
set start [int $start ]
set end [int $end ]
set counter 0
if { $start > 1 } { set counter $start }
set end $end
set prime_counting_function 0
while { $counter < $end } {
incr counter
incr prime_counting_function [isprime $counter ]
}
return $prime_counting_function }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global switch_factor big_giant_list legendre_function
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set L1 $side1
set L2 $side2
set N1 $side2
set switch_factor $side3
set approx_number_primes [/ $N1 [log $N1 ] ]
set legendre_function [/ $N1 [- [log $N1 ] 1.08366 ] ]
# conditions, all numbers real and positive.
# conditions L1 =! 1 and L2 > L1, otherwise division by zero and undefined Q's.
# if { $L1 == 1.0 } { set $L1 0.0 }
set approx_number_primes_interval_start [/ $L1 [log $L1 ] ]
set approx_number_primes_over_interval [- [/ $L2 [log $L2 ] ] [/ $L1 [log $L1 ] ] ]
set side4 $approx_number_primes
set side5 $legendre_function
set side6 $approx_number_primes
set side7 $approx_number_primes_interval_start
set side8 $approx_number_primes_over_interval
if { $switch_factor > 0 && $L2 < 200 } { exact_solution }
}
proc listprimes { aa bb} {lappend booboo 2.0; for {set i 1} {$i<=$bb} {incr i 2} { if {[isprime $i] } {lappend booboo [expr 1.*$i] } };return $booboo}
#returns list of prime numbers from aa to bb, usage [listprimes 0 25],
# answer is 2.0 3.0 5.0 7.0 11.0 13.0 17.0 19.0 23.0,
# list returned as real numbers, not counting 1.0 unity
proc exact_solution {} {
global side1 side2 side3 side4 side5
global side6 side7 side8 big_giant_list prime_counting
set big_giant_list [ listprimes $side1 $side2 ]
set side8 [ llength $big_giant_list ]
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global switch_factor big_giant_list legendre_function
global testcase_number
console show;
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| testcase number:|$testcase_number | |&"
puts "&| $side1 :|interval L1 | |&"
puts "&| $side2 :|end number L2 | |& "
puts "&| $side3 :|optional,if one, invoke exact solution (? long) | |& "
puts "&| $side4 :|answers: gauss function ~number_primes| |&"
puts "&| $side5 :|legendre function ~number_primes| |&"
puts "&| $side6 :|gauss approx_number_primes | |&"
puts "&| $side7 :|gauss approx_number_primes_interval_start | |&"
puts "&| $side8 :|gauss number_primes_over_interval | |&"
puts "&| $legendre_function :|legendre_function number_primes_N1| |&"
if {$switch_factor > 0.0} { puts "&| [prime_counting_function $side1 $side2 ] :|prime_counting_function over interval| |&" }
if {$switch_factor > 0.0 && $side2 < 190.} {puts "&| $big_giant_list :|list number_primes_over_interval | |&" }
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 0.0 1E1 1.0 4.3 8.20 4.3 0.00 4.30}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 0.0 5.0 1.0 3.1 9.50 3.1 0.00 3.10 }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 1E3 1E6 1.0 7E5 7E5 72382.0 0.0 72382.0 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Gauss Approximate Number of Primes Calculator"Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
Console program used to build csv spreadsheet charts.
# autoindent from ased editor
# console program for graph numbers
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# TCL WIKI , 12dec2016
console show
package require math::numtheory
#namespace path {math::numtheory}
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
proc factors {} {
set counter 0
set prime_counting_function 0
while {$counter < 500} {
puts " [* $counter 1.] , [/ [* $counter 1.] [log [* $counter 1.]] ], [isprime $counter ], $prime_counting_function "
incr counter
incr prime_counting_function [isprime $counter ]
}
return }
factorsconsole output
2.0 , 2.8853900817779268, 1, 1 3.0 , 2.7307176798805122, 1, 2 4.0 , 2.8853900817779268, 0, 2 5.0 , 3.1066746727980594, 1, 3 6.0 , 3.3486637593074837, 0, 3 7.0 , 3.5972883965882549, 1, 4 8.0 , 3.8471867757039027, 0, 4 9.0 , 4.0960765198207678, 0, 4 10.0 , 4.3429448190325175, 0, 4
# under test, biasing approx. from interval to save computer time
proc prime_counting_function { start end } {
set counter 0
if { $start > 1 } { set counter [int $start ] }
set end [int $end ]
set prime_counting_function 0
while { $counter < $end } {
incr counter
incr prime_counting_function [isprime $counter ]
}
return $prime_counting_function }
proc biased_count { N1 } {
set N1 [int $N1 ]
set bias1 [* 1. [ prime_counting_function [int [* $N1 .99] ] $N1 ]]
set bias2 [* 1. [ prime_counting_function $N1 [int [* $N1 1.01]] ]]
puts " $bias1 "
puts " $bias2 "
set bias 1.
set approx_number_primes 1.
set bias [expr $bias2/ double($bias1) ]
puts " $bias $bias2 $bias1 "
set approx_number_primes [* [/ $N1 [log $N1 ] ] $bias ]
return $approx_number_primes
}Console program for devil's notch
# pretty print from autoindent and ased editor
# testing devil's notch
# prime number function from TCLLIB
# written on Windows XP
# working under TCL version 8.6.6
# gold on TCL WIKI , 20dec2017
package require Tk
package require math::numtheory
package require math::constants
#package require math::bigfloat
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::constants }
console show
# corrected legendre_function
proc leg {N1 N2 } {
set legendre_function [/ $N1 [- [ ::tcl::mathfunc::log $N1 ] 1.08366 ] ]
set legendre_functionx [/ $N2 [- [ ::tcl::mathfunc::log $N2 ] 1.08366 ] ]
return [- $legendre_functionx $legendre_function ]
}
set numberx [ ::math::numtheory::prime_counting_functionx 450 550 ]
puts "prime counting function $numberx corrected legendre [ leg 450. 550. ] "
set numberx [ ::math::numtheory::prime_counting_functionx 550 650 ]
puts "prime counting function $numberx corrected legendre [ leg 550. 650. ] "
set numberx [ ::math::numtheory::prime_counting_functionx 650 750 ]
puts "prime counting function $numberx corrected legendre [ leg 650. 750. ] "
# padded statements into <local> ::math::numtheory::prime_counting_functionx
# for list of primes in interval
#if {[::math::numtheory::isprime $counter ] } { lappend lister $counter }
# }
# puts $listergold This page is copyrighted under the TCL/TK license terms, this license .
Comments Section
Please place any comments here, Thanks.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |