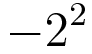**
expr "raise to power" operator, similar to pow function
Returns an integer value if both arguments are integers, and double-precision floating-point otherwise.
For integer-only arguments:
- The left operand may be any integer from Tcl's unlimited integer range.
- The right operand is limited to a max integer value of 268435455 (0xfffffff) (i.e., 28 bits) (unless the left operand is -1, 0, or 1, so that the answer is trivial).
- Expect to wait a long while for [expr 2**0xfffffff] to return.
If either argument is a floating-point value, this operator just call's the C math library pow() function behind the scenes.
Precedence
During early 2009, a thread broke out in the comp.lang.tcl usenet group discussing the observation that Tcl's calculation for
puts [expr {-2**2}]surprised someone who was expecting that to mean
puts [expr {-(2**2)}while Tcl's operator precedence rules cause it to mean
puts [expr {(-2)**2}What this does mean is that it is consistently possible to interpret -2 as minus two; no other operators around can change the interpretation.
It also means the answer you get will be different than most, if not all, other computer programming languages.
AMG: Is this set in concrete? I was recently surprised by this behavior, not for the first time, and likely not for the last time. I'm hard pressed to think of any case where it's important that - have higher precedence than **, especially since Tcl expr doesn't do complex numbers.
RLE: (2012-03-07) The problem is that the raw (no parens) equation is requesting expr to calculate this value:
Does that mean the negative of the square of two, or does it mean the square of negative two? If I am remembering my math correctly from way too long ago, I would interpret that equation to mean the square of minus two, which would result in four, just as Tcl produces.
AMG: Typically exponents have precedence over multiplication [L1 ], and I suggest that negation is multiplication. I take your expression to mean negative four, and my TI-89 agrees. Naturally, there's debate over this point [L2 ]. While Tcl's interpretation may be valid, it's also not very useful. What's the point in applying negation first, when Tcl doesn't have complex numbers?
RLE: (2012-03-09) Were you able to directly enter the algebraic equation into your TI-89? Because otherwise, the TI-89 would be agreeing with how you entered the equation. I.e., if you entered it this way -(2^2) you'll get -4, but if you enter it this way: (-2)^2 you'll get 4.
Note, I'm not disagreeing with what you cite via. Wikipedia, as I said, "my math ... from way too long ago", and the Wikipedia article does state that -2^2 should typically be interpreted as -(2^2), although it does indicate that this is a point of some disagreement. I think a portion of the disagreement may arise depending on whether one interprets -2 to mean -1*2 or to mean the number "negative 2" (i.e., a free standing, independent, "number" called "minus two").
To bring this back to a bit of Tcl discussion, items like this are why I very long ago built up the habit of simply using extra parens to force the evaluation order I wanted, even if that order was the default to begin with. Getting burned more than a few times when a computation didn't produce an expected result due to a slight disagreement between what I thought the language/system/spreadsheet should be doing vs. what it was actually doing led me to simply add defensive parens in all but the simplest of formula evaluation situations. Does this habit possibly slow things down slightly, yes. Is the slowdown worth saving hours of head scratching time figuring out why an answer is not what I expected, well to me, yes it is worth saving that time.
- DKF: Mind you, it only slows things down during expression compilation (and that's very marginal unless you've got horrendous expressions). Execution will be just as fast.
- RLE: Thanks DKF, that is a good fact to know, that my "paranoia" habit does not actually cost much at all during runtime.
AMG: Entering -2^2 into my TI-89 produces -4, as does -(2^2). It applies exponentiation before negation. Yes, you're right, the disagreement stems from -2 being seen as "negative 2" versus "2" with a negation operator applied, where negation is equivalent to multiplication by negative 1. I believe the latter interpretation is closer to how the code sees things, since we also have things like ---------2.
From comp.lang.tcl:
In math:
a**0 == 1, a != 0, and 0**a == 0, a != 0. 0**0 is indeterminate
In Tcl (8.5.7):
expr {0**0} => 1 Here is an interesting example which tests the precedence of ** and - and demonstrates the right to left application of **:
expr {2**-2**2} => 16 Force delayed application of -:
expr {2.0**-(2**2)} => .0625 Force left to right exponentiation:
expr {(2.0**-2)**2} => .0625 Unambiguous:
expr {(2.0)**((-2)**2)} => 16