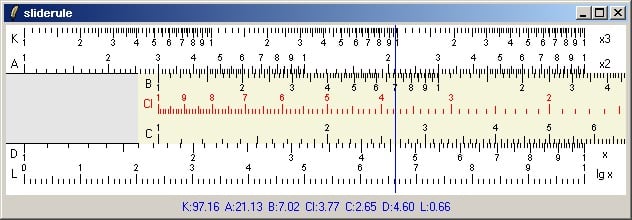
A little slide-rule
Richard Suchenwirth 2003-08-31 - The slide rule was an analog, mechanical device for approximate engineering computing, made obsolete by the pocket calculator since about the 1970-80s. The basic principle is that multiplication is done by adding logarithms, hence most of the scales are logarithmic, with uneven increments.
This fun project recreates a slide rule (roughly an Aristo-Rietz Nr. 89 with 7 scales - high-notch ones had up to 24) with a white "body" and a beige "slide" which you can move left or right with mouse button 1 clicked, or in pixel increment with the <Shift-Left>/<Shift-Right> cursor keys. Finally, the blue line represents the "mark" (how is that correctly called? "runner"? "slider"?) (it's called a "cursor") which you can move with the mouse over the whole thing to read a value. Fine movements with <Left>/<Right>.
Due to rounding errors (integer pixels), this plaything is even less precise than a physical slide rule was, but maybe you still enjoy the memories... The screenshot shows how I found out that 3 times 7 is approx. 21... (check the A and B scales).
For another mathematical toy, see TkSoroban.
proc ui {} {
set width 620
pack [canvas .c -width $width -height 170 -bg white]
pack [label .l -textvariable info -fg blue] -fill x
.c create rect 0 50 $width 120 -fill grey90
.c create rect 0 50 $width 120 -fill beige -outline beige \
-tag {slide slidebase}
.c create line 0 0 0 120 -tag mark -fill blue
drawScale .c K x3 10 5 5 log10 1 1000 186.6666667
drawScale .c A x2 10 50 -5 log10 1 100 280
drawScale .c B x2 10 50 5 log10 1 100 280 slide
drawScale .c CI 1/x 10 90 -5 -log10 1 10 560 slide
drawScale .c C x 10 120 -5 log10 1 10 560 slide
drawScale .c D x 10 120 5 log10 1 10 560
drawScale .c L "lg x" 10 160 -5 by100 0 10 5600
bind .c <Motion> {.c coords mark %x 0 %x 170; set info [values .c]}
bind .c <1> {set x %x}
bind .c <B1-Motion> {%W move slide [expr {%x-$x}] 0; set x %x}
bind . <Shift-Left> {.c move slide -1 0; set info [values .c]}
bind . <Shift-Right> {.c move slide 1 0; set info [values .c]}
bind . <Left> {.c move mark -1 0; set info [values .c]}
bind . <Right> {.c move mark 1 0; set info [values .c]}
}
proc drawScale {w name label x y dy f from to fac {tag {}}} {
set color [expr {[string match -* $f]? "red": "black"}]
$w create text $x [expr $y+2*$dy] -text $name -tag $tag -fill $color
$w create text 600 [expr $y+2*$dy] -text $label -tag $tag -fill $color
set x [expr {[string match -* $f]? 580: $x+10}]
set mod 5
set lastlabel ""
set lastx 0
for {set i [expr {$from*10}]} {$i<=$to*10} {incr i} {
if {$i>100} {
if {$i%10} continue ;# coarser increments
set mod 50
}
if {$i>1000} {
if {$i%100} continue ;# coarser increments
set mod 500
}
set x0 [expr $x+[$f [expr {$i/10.}]]*$fac]
set y1 [expr {$i%(2*$mod)==0? $y+2.*$dy: $i%$mod==0? $y+1.7*$dy: $y+$dy}]
set firstdigit [string index $i 0]
if {$y1==$y+$dy && abs($x0-$lastx)<2} continue
set lastx $x0
if {$i%($mod*2)==0 && $firstdigit != $lastlabel} {
$w create text $x0 [expr $y+3*$dy] -text $firstdigit \
-tag $tag -font {Helvetica 7} -fill $color
set lastlabel $firstdigit
}
$w create line $x0 $y $x0 $y1 -tag $tag -fill $color
}
}
proc values w {
set x0 [lindex [$w coords slidebase] 0]
set x1 [lindex [$w coords mark] 0]
set lgx [expr {($x1-20)/560.}]
set x [expr {pow(10,$lgx)}]
set lgxs [expr {($x1-$x0-20)/560.}]
set xs [expr {pow(10,$lgxs)}]
set res K:[format %.2f [expr {pow($x,3)}]]
append res " A:[format %.2f [expr {pow($x,2)}]]"
append res " B:[format %.2f [expr {pow($xs,2)}]]"
append res " CI:[format %.2f [expr {pow(10,-$lgxs)*10}]]"
append res " C:[format %.2f $xs]"
append res " D:[format %.2f $x]"
append res " L:[format %.2f $lgx]"
}
proc pow10 x {expr {pow(10,$x)}}
proc log10 x {expr {log10($x)}}
proc -log10 x {expr {-log10($x)}}
proc by100 x {expr {$x/100.}}
#--------------------------------
ui
bind . <Escape> {exec wish $argv0 &; exit}Judging from some web sites, it appears as if the parts of a slide-rule are called "stator" (big white), "slide" (thin beige), and "cursor" (transparent little thing, blue line in the above example). Also, there's a roughly comparable emulation in Java at http://www.cs.utsa.edu/~wagner/slide/Slide5.html
Absolutely Amazing for such little code! Nicely DONE!
AM I can add a personal touch to the end of the slide-rule era:
When I took my final exams in secondary school (in 1978-79), there was a debate whether electronic calculators should be allowed. The decision was no, because they were still pretty expensive at the time and allowing them might force students who did not yet have one to buy such a thing.
It was, however, a prequisite when I went to university in that same year. After school I have used it sporadically, but I envy my father for his possessing a very smooth wooden slide-rule in a nice wooden casing.
This page inspired me to look into another obsolete instrument, the klepsydra.
Anyone ever build a Tcl toy circular slide rule [L1 ] ?
GWM I also used slide rules for A level exams in 1970 - this version doesn't have the sliding part sticking out of the end which was useful for taking people's eyes out. I met my first 'pocket' calculator (an HP with RPN notation costing some £200, or $500 at the time) working for ESTEC in 1972; it had some 20 math functions and the head of department took it to the Munich Olympics to calculate the speed of the runners. I discovered that selecting the arc-tan function repeatedly eventually produced a constant value (89.35883916.. you can repeat this with a modern calculator) - just a short way from discovering Mandelbrot sets (this solves the equation f=atan(f)). One colleague had an Otis King cylindrical slide rule giving an effective 200 cm long slide rule (all of 5 sig figs accuracy!). See http://www.hpmuseum.org/srcyl.htm for pictures of slide rules. The figures in this note are probably distorted by my memory, do not rely on them for correctness.
RFox - I used a Keufel-Esser Log-Log Duplex Decitrig model slide rule throughout graduate school, especially, while being a TA at UIUC's PHYS 101 class. I did this mostly to attempt to discourage students from reacting to a problem by ducking their heads into their calculator, rather than taking the time to analytically solve their problems first... Richard.. Having the cursor location shown numerically at the bottom of the stator is cheating ;-) The whole point of being a slide-rule whiz was to learn to estimate/interpolate by eye where the cursor was on the stator or slide.
GS (040915) Don't forget the Curta [L2 ], one of the first pocket calculator (mechanical).
US Changing the proc ui to the following makes it, at least for me, better usable. Left button clicked and moved on the 'stator' moves the 'cursor', whereas clicking and moving on the 'slide' moves the 'slide'.
proc ui {} {
set width 620
pack [canvas .c -width $width -height 170 -bg white]
pack [label .l -textvariable info -fg blue] -fill x
.c create rect 0 0 $width 170 -fill white -outline white \
-tag stator
.c create rect 0 50 $width 120 -fill grey90
.c create rect 0 50 $width 120 -fill beige -outline beige \
-tag {slide slidebase}
.c create line 0 0 0 120 -tag mark -fill blue
drawScale .c K x3 10 5 5 log10 1 1000 186.6666667 stator
drawScale .c A x2 10 50 -5 log10 1 100 280 stator
drawScale .c B x2 10 50 5 log10 1 100 280 slide
drawScale .c CI 1/x 10 90 -5 -log10 1 10 560 slide
drawScale .c C x 10 120 -5 log10 1 10 560 slide
drawScale .c D x 10 120 5 log10 1 10 560 stator
drawScale .c L "lg x" 10 160 -5 by100 0 10 5600 stator
.c bind stator <B1-Motion> {.c coords mark %x 0 %x 170; set info [values .c]}
.c bind stator <1> {.c coords mark %x 0 %x 170; set info [values .c]}
.c bind slide <1> {set x %x}
.c bind slide <B1-Motion> {%W move slide [expr {%x-$x}] 0; set x %x}
bind . <Shift-Left> {.c move slide -1 0; set info [values .c]}
bind . <Shift-Right> {.c move slide 1 0; set info [values .c]}
bind . <Left> {.c move mark -1 0; set info [values .c]}
bind . <Right> {.c move mark 1 0; set info [values .c]}
}TP Here's a nice link on how to actually use a slide rule: http://www.sliderulemuseum.com/SR_Course.htm The page includes an HTML version that you can open in a browser.