Babylonian False Position Algorithm and eTCL demo example calculator, numerical analysis
Babylonian False Position Algorithm and eTCL demo example calculator, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 12Dec2018
- Babylonian False Position Algorithm and eTCL demo example calculator, numerical analysis
- Pseudocode Section
- Appendix Code
- HIdden Comments Section
gold Here is some eTCL starter code for Babylonian false position algorithm.
The Babylonian false position algorithm was loaded into an eTCL calculator. The Babylonians did not use algebra notation, so the reader will have to bear some anachronisms in the eTCL pseudocode. The field is assumed to be a square or right rectangle. The area of the field and the short side constraint ratio are given values. The tablet has a set of line by line calculations which effectively guess the two sides of a field and compute a scale factor from the sqrt ratio of true area to the product of the guessed or false position sides. The short and long false position sides are constrained, multiplied, and rescaled to calculate the short and long sides of the field. The answer was checked to see if product of the corrected short and long sides equal the given initial area. For restating the problem in a computer algorithm, the sides and field area will be in meters and square meters, respectively.
The Babylonian false position algorithm, in particular, is an intriguing example of how our ancestors used logic and calculation to solve complex problems. The TCL calculator is a modern tool that can help us understand and apply these ancient methods in our own work. By loading the Babylonian false position algorithm into the calculator, we can see how this technique was used to find the correct dimensions of a field, given the area and the short side constraint ratio. It is interesting to note that the Babylonians did not use algebra notation, which may seem anachronistic to us today. However, their use of this algorithm shows that they were able to think logically and solve complex problems without the benefit of modern mathematical notation.
The field is assumed to be a square or right rectangle, which is a common assumption in geometry. By applying the constraints of the short side and the given area, the algorithm effectively guesses the two sides of the field and computes a scale factor from the square root of the ratio of the true area to the product of the guessed or false position sides. The short and long false position sides are then constrained, multiplied, and rescaled to calculate the short and long sides of the field. The answer is checked to see if the product of the corrected short and long sides equal the given initial area.
While this false position algorithm may seem complex, it is a powerful tool that can help us better understand and apply ancient mathematical methods to modern problems. By restating the problem in a computer algorithm, we can use tools like the TCL calculator to solve complex problems more efficiently and accurately. Overall, the Babylonian false position algorithm is a fascinating example of how our ancestors used logic and calculation to solve complex problems. The Babylonian false position algorithm serves as a reminder of the incredible potential of human ingenuity and innovation.
Pseudocode Section
# using pseudocode for Babylonian false position algorithm
# possible problem instances include separate tables for cubes n*n*n and quasi_cubes
true_area = supplied value
false_long_side = initial guess
false_short_side = 2/3 length, supplied ratio
set false_area [expr $false_long_side*$false_short_side ]
initialise correction = 0.25
correction = sqrt (true_area / false_area)
long_side = false_long_side * correction
short_side = false_short_side * correction
check_answer long_side * short_side =? true_area (yes/no)
set answers and printout with resulting valuesTestcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
Testcase 1
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 1000.0 : | true area meters squared | |
| 0.6660 : | short side is x of long (ratio) | |
| 100.0 : | initial guess of long side meters | |
| 66.600 : | answers: false short side meters | |
| 6660.000 : | false area meters squared | |
| 0.387 : | correction factor (ratio) | |
| 25.806 : | short side meters | |
| 38.7492 : | long side meters |
Testcase 2
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 1200.0 : | true area meters squared | |
| 0.666 : | short side is x of long (ratio) | |
| 120.0 : | initial guess of long side meters | |
| 79.920 : | answers: false short side meters | |
| 9590.399 : | false area meters squared | |
| 0.353 : | correction factor (ratio) | |
| 28.270 : | short side meters | |
| 42.447 : | long side meters |
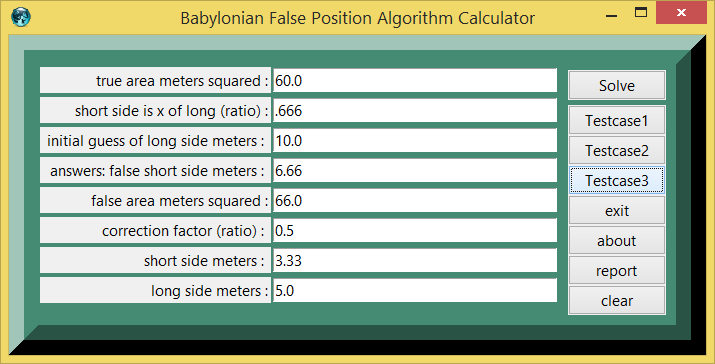
Testcase 3
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 60.0 : | true area meters squared | |
| 0.666 : | short side is x of long (ratio) | |
| 10.0 : | initial guess of long side meters | |
| 6.660 : | answers: false short side meters | |
| 66.599 : | false area meters squared | |
| 0.949 : | correction factor (ratio) | |
| 6.321 : | short side meters | |
| 9.491 : | long side meters |
Screenshots Section
figure 1.
References:
- Wikipedia <False position method>
- Galdino, Sérgio (2011). "A family of regula falsi root-finding methods".
- Proceedings of 2011 World Congress on Engineering
- Mathematical Treasure: Old Babylonian Area Calculation, uses ancient method
- Frank J. Swetz , Pennsylvania State University
- Wikipedia, see temple of Edfu, area method used as late as 200 BC in Egypt.
- Oneliner's Pie in the Sky
- One Liners
- Category Algorithm
- Babylonian Number Series and eTCL demo example calculator
- Brahmagupta Area of Cyclic Quadrilateral and eTCL demo example calculator
- Gauss Approximate Number of Primes and eTCL demo example calculator
- Land surveying in ancient Mesopotamia, M. A. R. Cooper
- Sumerian Approximate Area Quadrilateral and eTCL Slot Calculator Demo Example , numerical analysis
- Thomas G. Edwards, Using the Ancient Method of False Position to Find Solutions
- Joy B. Easton, rule of double false position
- Vera Sanford, rule of false position
- www.britannica.com, topic, mathematics false position
- Sumerian Equivalency Values, Ratios, and the Law of Proportions with Demo Example Calculator
- Babylonian Sexagesimal Notation for Math on Clay Tablets in Console Example
Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# Babylonian False Position Algorithm calculator
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI, 15jan2017
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} { true area meters squared :} }
lappend names { short side is x of long (ratio) :}
lappend names { initial guess of long side meters : }
lappend names { answers: false short side meters : }
lappend names { false area meters squared :}
lappend names { correction factor (ratio) : }
lappend names { short side meters : }
lappend names { long side meters :}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Babylonian False Position Algorithm
from TCL WIKI,
written on eTCL "
tk_messageBox -title "About" -message $msg }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set true_area $side1
set false_long $side3
set false_short [* $false_long $side2 ]
set false_area [* $false_long $false_short ]
set correction_ratio .25
set correction_ratio [/ $true_area $false_area]
set correction_ratio [sqrt $correction_ratio ]
set side4 $false_short
set side5 $false_area
set side6 $correction_ratio
set side7 [* $false_short $correction_ratio ]
set side8 [* $side3 $correction_ratio ]
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number reference_factor flag
console show;
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |& "
puts "&| $side1 :|true area meters squared | |&"
puts "&| $side2 :|short side is x of long (ratio)| |& "
puts "&| $side3 :|initial guess of long side meters| |& "
puts "&| $side4 :|answers: false short side meters| |&"
puts "&| $side5 :|false area meters squared | |&"
puts "&| $side6 :|correction factor (ratio) | |&"
puts "&| $side7 :|short side meters | |&"
puts "&| $side8 :|long side meters | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 1000.0 .666 100.0 66.0 6660.0 0.38 26. 38.}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 1200. .666 120. 79. 9590.0 0.35 28. 42. }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 60.0 .666 10.0 6.66 66.0 0.5 3.33 5.0 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Babylonian False Position Algorithm Calculator" Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
gold12Dec2018. This page is copyrighted under the TCL/TK license terms, this license .
HIdden Comments Section
Please place any comments here with your wiki MONIKER and date, Thanks.gold12Dec2018