Babylonian False Shares Algorithm, numerical analysis, history of math & computers
Babylonian False Shares Algorithm, numerical analysis, history of math & computers
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 12Dec2018
- Babylonian False Shares Algorithm, numerical analysis, history of math & computers
- Introduction
- Pseudocode Setup for false shares method
- Inheritance Testcases
- Testcases Section
- Testcase 1a, Tablet YBC10722
- Testcase 1b, Tablet AO8862, (2nd t) from Larsa, rated at 1739/1749 BCE
- Testcase 1c, Tablet AO8862, (1st t) from Larsa, rated at 1739/1749 BCE
- Testcase 2, "Talmudic" Inheritance from Ben Erza
- Testcase 3, Gentile Inheritance rule from Ibn Ezra
- Testcase 4, Inheritance under Islamic law
- Testcase 5, Inheritance under Islamic law
- Testcase 6, Double portion, Ancient Jewish Inheritance
- Testcase 7, Sum of Sequence
- Screenshots Section
- References:
- Testcases Section
- Appendix Code
- Comments Section
Introduction
gold Here are some TCL calculations on the false shares method from Babylonian math problems. The false shares method or false shares problem is of historical interest, but seems to be the Babylonian tool of choice for expanding into new math horizons. Most of the testcases involve replicas or models, using assumptions and rules of thumb.
In the cuneiform math problems and coefficient lists on clay tablets, there are coefficient numbers which were used in determining the amount of materials and the daily work rates of the workers. In most cases, the math problem is how the coefficient was used in estimating materials, work rates, and math problems. One difficulty is determining the effective magnitude or power of the number coefficient in the base 60 notation. In cuneiform, numbers in base 60 are written using a relative notation. For example, 20 could represent either 20*3600,20,20/60, 20/3600, or even 1/20. The basic dimensions and final tallies were presented in the cuneiform accounts on clay tablets, but some calculations, some units, and some problem answers (aw shucks!) were left off the tablet. Successive or iterated math solutions are called algorithms and the Babylonian methods are some of the earliest algorithms documented circa 1600 BCE. The TCL procedures are descendants of this idea. The Babylonians did not use algebra notation, decimal notation, or modern units, so the reader will have to bear some anachronisms in the TCL code. At least one approach for the modern reader and using modern terminology is to develop the implied algebraic equations and decimal equivalents from the cuneiform numbers. Then the TCL calculator can be run over a number of testcases to validate the algebraic equations.
Babylonian False Shares Method
The Babylonian false shares method algorithm from clay tablets was loaded into a TCL calculator. The Babylonians did not use algebra notation, so the reader will have to bear some anachronisms in the TCL pseudocode. The false shares method is defined as the method used by scribes to portion multiple shares of a quantity, including estate inheritances, wages, land divisions, and bricks. Successive or iterated math solutions are called algorithms and the false shares method algorithm is one of the earliest algorithms documented. The TCL procedures are descendants of this idea.
Pseudocode Setup for false shares method
Setup for Pseudocode. From the tablet YBC10722, the work standard for moving 9*60 bricks over 30 rods per day is 15 units of barley, ref Friberg. In this testcase, 4 men share the work and pay in proportions of 7,11,13,14. The Babylonians did not use algebraic notation, but the algebraic solution is shown here for quicker understanding for the modern reader and for psuedocode for the TCL procedure. Tabbing the false shares as $X, the initial setup is 7*$X+11*$X+13*$X+14*$X=15,45*$X=15, $S=(sum of shares)/ (total pay units), $S= 15/ 45= (1/3) unit pay per shares. 1st= 7*(1/3),2nd=11*(1/3),3ird=13*(1/3),4th=14*(1/3). Check that expr { 7*(1./3)+11*(1./3)+13*(1./3)+14*(1./3) } = 15. Order here is increasing pay, but (tablet) norm was that order was in decreasing amounts. Ref. Friberg on YBC10722. Ref AO8862, four-sided prism from Larsa, was rated at 1739/1749 BCE. Note: AO8862 sets the problem up but the method of solution was not completely recorded on AO8862. Some uncertaincy must be recognized in the problem solution on both tablets YBC10722 and AO8862 . Note: There are some Babylonian problems where the setup is multiplied by an integer (usually 2 or 3 ) at some point in the method and later factored out of the solution. Check that expr {(2*15.)/(2*45.)} = (1/3). The average of the sequence {7 11 13 14} was expr {(7 +11 +13 +14)/4. } or 11.25.
Pseudocode Section
# using Pseudocode for Babylonian false shares method
# entry 1) quantity for sharing
# 4) { 1 2 3 4 } share ratios in sequence list.
# possible Babylonian style solution
# scribes often put in columns from off tablet computations
entries calc decimal base_60 fraction
7 7*2 7*(1/3) 2.3333 2+20/60
11 11*2 11*(1/3) 3.6666 3+40/60
13 13*2 13*(1/3) 4.3333 4+20/60
14 14*2 14*(1/3) 4.6666 4+40/60
sum = 90
share rate = 15*2/90 = 30/90. = 1/3 = 20/60 = reciprocal 3
expr { 7*(20/60.)+11*(20/60.)+13*(20/60.)+14*(20/60.) } = 15
# try to avoid numbers like 7,11,13 in base_60 by odd*even=even
# numbers like 7,11,13 are prime numbers and can not be factored
# to produce regular closed form reciprocals in base_60.
# expr { ( 7*(3.)+11*(3.)+13*(3.)+14*(3.))*(1/9.) } = 15The tablet AO8862 from Larsa is calculating shares for four men on a complex or combined job. The tablet AO8862 is almost a sui generis, but there are later tablets from Umma in UR3 that round out some of the Sumerian customs. An overseer would give the scribe small hand tablets or oral instructions. The scribe would figure the wages or shares of the workers and tally the amounts from the customary work quotas. The usual low skilled pay was two bowls of cracked barley per man. Uncommon, but half and quarter days are found in the accounts. Continuing with the scenario, a half day would be one bowl and a quarter day would be 1/2 bowl. However, AO8862 is figuring the pay to 1/3600 of a bowl as volume unit. Barley was not usually measured to 1/3600 bowl (bowl = liter), but some water weights and time measures in the water clocks may approach this precision. Not sure that plausible hours, double hours, or quarter days as Sumerian time units could be reduced to the {7 11 13 14} multiple ratio given. With the calculator, the 12 hours of the Sumerian workday was portioned with {7 11 13 14} multiple ratio and the decimal hours were { 1.8667 2.9333 3.4667 3.7333}. The Sumerians used other units of time and the double hours in decimal units were { 0.9333 1.4667 1.7333 1.8667}. In many cases the multiple ratio can be reduced in the calculator and give the same answer. For example, 20 portioned with { 4 4 4 4 } gives the same result in the calculator as the reduced { 2 2 2 2 }. However, 3 ratios in sequence {7 11 13 14} are prime and can not be reduced to smaller whole numbers. It is possible the false shares algorithm is being tested or demonstrated in AO8862 that the algorithm will work with prime numbers and return accurate pay. Some of the Babylonian algorithms did not work with prime numbers (irregular in base_60) or had to be adapted-supplemented because the prime numbers could not be factored.
The tablet AO8862 from Larsa was rated at 1739/1749 BCE to (as recent as) 1720 BCE, sophisticated but near end of Larsa math tradition. Concept for sum of sequence(s) would be necessary for false shares algorithm, whether terms multiplied by integer or not in the algorithm. At least in the available problems, the published sequences have 4 to 5 terms. Sum of sequences has many implications in history of math.
Inheritance Testcases
Rabbi Abraham Ibn Ezra (1140 CE, born Tudela, Navarre,(or modern)Spain) has an interesting discussion on proportional division and other "just" divisions under Jewish law in the Talmud and commentaries. The available clay tablets on the false shares method is roughly from 1800 to 1500 BCE, but Rabbi Ibn Ezra expounds on proportional division from some "gentile" or "foreign" source. The Babylonian false share methods did not have a free ride, but were condemned by several sources in mainstream Talmudist and Christian traditions. It would be interesting to include or compare Talmudist division in the calculator. The calculator handles simple cases of Islamic inheritance as it stands.
Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
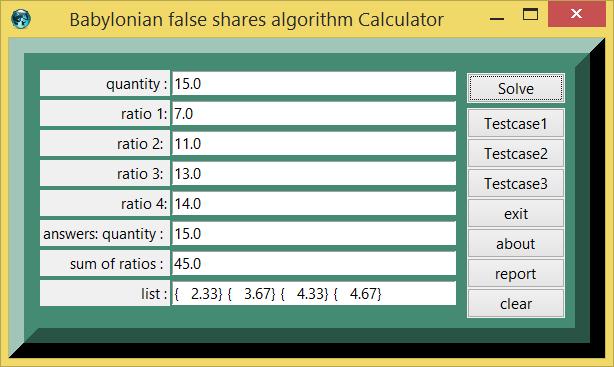
Testcase 1a, Tablet YBC10722
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 15.0 : | quantity | |
| 7.0 : | ratio 1 | |
| 11.0 : | ratio 2 | |
| 13.0 : | ratio 3 | |
| 14.0 : | ratio 4: | |
| 15.0 : | answers: quantity | |
| 45.0 : | sum of ratios | |
| 2.3333 3.6666 4.3333 4.6666 : | list | |
| 2.3333 3.6666 4.3333 4.6666 : | check sum =? 15 |
Testcase 1b, Tablet AO8862, (2nd t) from Larsa, rated at 1739/1749 BCE
| table 1b | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 1b: | testcase_number | |
| 20.0 : | quantity | |
| 7.0 : | ratio 1 | |
| 11.0 : | ratio 2 | |
| 13.0 : | ratio 3 | |
| 14.0 : | ratio 4: | |
| 20.0 : | answers: quantity | |
| 45.0 : | sum of ratios | |
| { 3.11 4.89 5.78 6.22 } : | list |
Testcase 1c, Tablet AO8862, (1st t) from Larsa, rated at 1739/1749 BCE
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 20.0 : | quantity | |
| 1.0 : | ratio 1 | |
| 2.0 : | ratio 2 | |
| 3.0 : | ratio 3 | |
| 4.0 : | ratio 4: | |
| 5.0 : | ratio 5 | |
| 15.0 : | sum of ratios | |
| { 1.3333 2.6667 4.0000 5.3333 6.6667} : | list | modified program temp. for 5 entries |
Testcase 2, "Talmudic" Inheritance from Ben Erza
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 1000.0 : | quantity | |
| 67.0 : | son 1 | |
| 17.0 : | son 2 | |
| 9.0 : | son 3 | |
| 6.0 : | son 4: | |
| 1000.0 : | answers: quantity | |
| 6.0 : | sum of ratios | |
| 674.00 174.00 90.00 63.00 : | list | |
| algorithm needs substantial change for this result: |
Testcase 3, Gentile Inheritance rule from Ibn Ezra
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 1.0 : | quantity | |
| 1.0 : | ratio 1 | |
| 0.5 : | ratio 2 | |
| 0.333 : | ratio 3 | |
| 0.25 : | ratio 4: | |
| 1.0 : | answers: quantity | |
| 2.0832 : | sum of ratios | |
| 0.48 0.24 0.16 0.12 : | list | |
| 0.48 0.24 0.16 0.12 : | check sum =? 1 |
Testcase 4, Inheritance under Islamic law
| table 4 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 4: | testcase_number | |
| 1000.0 : | quantity | |
| 2.0 : | son 1 | |
| 2.0 : | son 2 | |
| 1.0 : | daughter 1 | |
| 1.0 : | daughter 2 | |
| 1000.0 : | answers: quantity | |
| 6.0 : | sum of ratios | |
| 333.33 333.33 166.67 166.67 : | list | |
| 333.33 333.33 166.67 166.67 : | check sum =? 1000 |
Testcase 5, Inheritance under Islamic law
---
| table 5 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 5: | testcase_number | |
| 1000.0 : | quantity | |
| 2.0 : | son 1 | |
| 2.0 : | son 2 | |
| 2.0 : | son 3 | |
| 2.0 : | son 4: | |
| 1000.0 : | answers: quantity | |
| 6.0 : | sum of ratios | |
| 250.00 250.00 250.00 250.00 : | list |
Testcase 6, Double portion, Ancient Jewish Inheritance
| table 6 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 6: | testcase_number | |
| 1000.0 : | quantity | |
| 2.0 : | ratio 1 | |
| 1.0 : | ratio 2 | |
| 1.0 : | ratio 3 | |
| 1.0 : | ratio 4: | |
| 1000.0 : | answers: quantity | |
| 5.0 : | sum of ratios | |
| 400.00 200.00 200.00 200.00 : | list |
Testcase 7, Sum of Sequence
| table 7 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 7: | testcase_number | |
| 15.0 : | quantity | |
| 1.0 : | ratio 1 | |
| 2.0 : | ratio 2 | |
| 3.0 : | ratio 3 | |
| 4.0 : | ratio 4: | |
| 5.0 : | ratio 5 | |
| 15.0 : | sum of ratios | |
| { 1.0000 2.0000 3.0000 4.0000 5.0000} : | list |
Screenshots Section
figure 1.
References:
- Bricks and mud in metro-mathematical cuneiform texts,
- Joran Friberg
- O. Neugebauer and A. Sachs, Mathematical Cuneiform Texts,
- American Oriental Society, Series 29. New Haven, 1945.
- A Remarkable Collection of Babylonian Mathematical Texts,
- Joran Friberg
- the historical origins of algebraic thinking, essay,
- Luis g. Radford
- Talmud, mathematical theories of arbitration , Oneill
- The Inheritance of Brothers and Sisters, Islamic (Sunni)
- Sequences and series in Old Babylonian mathematics,
- Duncan J Melville
- MS 2830, obv. A theme text with five inheritance problems,Joran Friberg .
- Oeis {7 11 13 14},
- Numbers n such that Mordell's equation y^2 = x^3 + n
- has no integral solutions.
- Oeis {7 11 13 14}, sums of three distinct powers of 2.
- Oeis {7 11 13 14}, Numbers n such that 16n+15 is prime.
- YBC10722 relates the quantity 15 with the sequence {7 11 13 14}!
- Otto Neugebauer, Mathematical Cuneiform Texts, YBC10722=Text p,
- ref. YBC4673
Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# Babylonian false shares algorithm calculator
# keyword proportional division in current math terms
# written on Windows XP on TCL
# working under TCL version 8.6
# gold on TCL WIKI, 20jan2018
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {quantity :} }
lappend names {ratio 1:}
lappend names {ratio 2: }
lappend names {ratio 3: }
lappend names {ratio 4:}
lappend names {answers: quantity : }
lappend names {sum of ratios : }
lappend names {list :}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Babylonian false shares algorithm
from TCL WIKI,
written on eTCL "
tk_messageBox -title "About" -message $msg }
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
#
# ::math::false_shares --
#
# Return the division of quantity by proportional division
#
# Arguments:
# val first value is quantity
# args other values are two or more given ratios
#
# Results: parts of quantity proportional division
#
# puts " [ ::math::false_shares 84 ] # zip
# for (::math::false_shares) # returns zero "
proc ::math::false_shares {quantity args} {
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
set sum 0
set false_share 2.
foreach val $args {
set sum [ expr { $sum + $val*$false_share } ]
}
foreach val $args {
lappend answer [format %7.2f [ expr { $val * ($quantity*1.)/($sum/$false_share) } ]]
}
set answer
}
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set answer2 [ ::math::false_shares $side1 $side2 $side3 $side4 $side5]
set sum_of_ratios [+ $side2 $side3 $side4 $side5 ]
set side6 $side1
set side7 $sum_of_ratios
set side8 $answer2
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
console show;
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |&"
puts "&| $side1 :|quantity | |&"
puts "&| $side2 :|ratio 1 | |& "
puts "&| $side3 :|ratio 2 | |& "
puts "&| $side4 :|ratio 3 | |&"
puts "&| $side5 :|ratio 4: | |&"
puts "&| $side6 :|answers: quantity | |&"
puts "&| $side7 :|sum of ratios | |&"
puts "&| $side8 :|list| |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { set side8 0 ; calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 15.0 7. 11.0 13.0 14.0 15. 7.0 15.0}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 120.0 1.0 2.0 3.0 4.0 120.0 6.0 20.0}
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 1.0 1.0 2.0 3.0 4.0 360.0 12.0 30.0}
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Babylonian false shares algorithm Calculator" Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
gold This page is copyrighted under the TCL/TK license terms, this license .
Comments Section
Please place any comments here, Thanks. x
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Toys and Games | Category Games | Category Application | Category GUI |