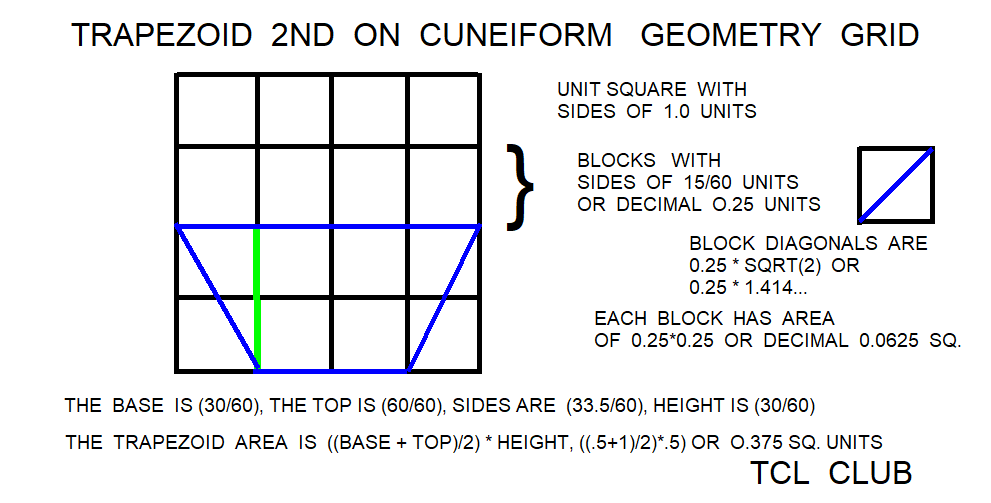
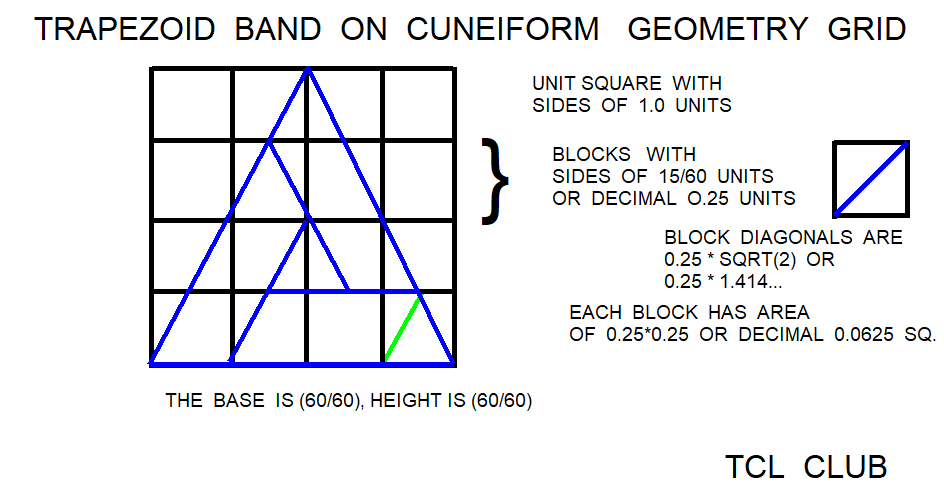
Babylonian Trapezoid Area V5
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 3/2/2024
- Appendix Code
- Hidden Comments Section
Title: Babylonian Trapezoid Area V5
Introduction
gold Here are some TCL calculations for trapezoid area using both conventional formulas and the Babylonian square law formula. The calculator uses modern units as meters for convenience to modern users and textbook examples. The units are not critical in the calculator internal math and any consistent units and output might be used like dollars to donuts. A number of Babylonian math problems have been found on Babylonian square law formula for trapezoid areas and volumes, ref Friberg.
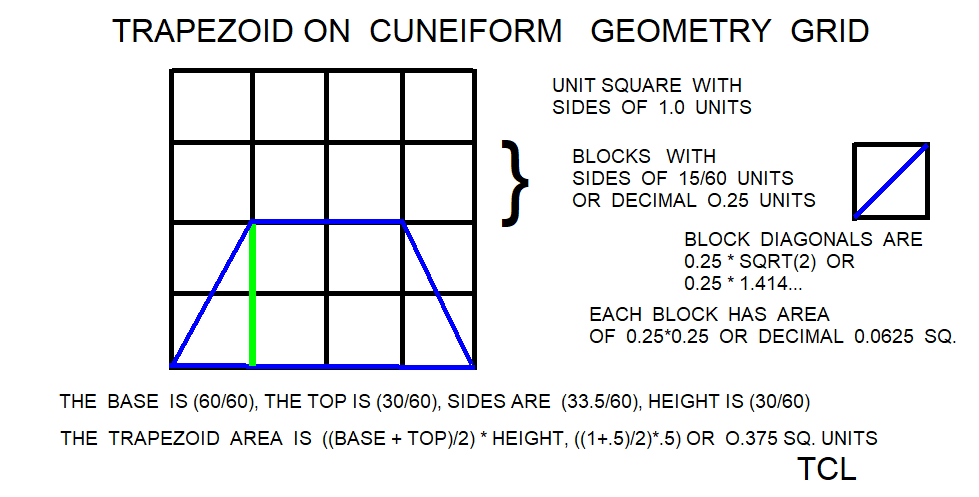
In the cuneiform math problems and coefficient lists on clay tablets, there are coefficient numbers which were used in determining the amount of materials and the daily work rates of the workers. In most cases, the math problem is how the coefficient was used in estimating materials, work rates, and math problems. One difficulty is determining the effective magnitude or power of the number coefficient in the base 60 notation. In cuneiform, numbers in base 60 are written using a relative notation. For example, 20 could represent either 20*3600,20,20/60, 20/3600, or even 1/20. The basic dimensions and final tallies were presented in the cuneiform accounts on clay tablets, but some calculations, some units, and some problem answers (aw shucks!) were left off the tablet. Successive or iterated math solutions are called algorithms and the Babylonian methods are some of the earliest algorithms documented circa 1600 BCE. The TCL procedures are descendants of this idea. The Babylonians did not use algebra notation, decimal notation, or modern units, so the reader will have to bear some anachronisms in the TCL code. At least one approach for the modern reader and using modern terminology is to develop the implied algebraic equations and decimal equivalents from the cuneiform numbers. Then the TCL calculator can be run over a number of testcases to validate the algebraic equations.
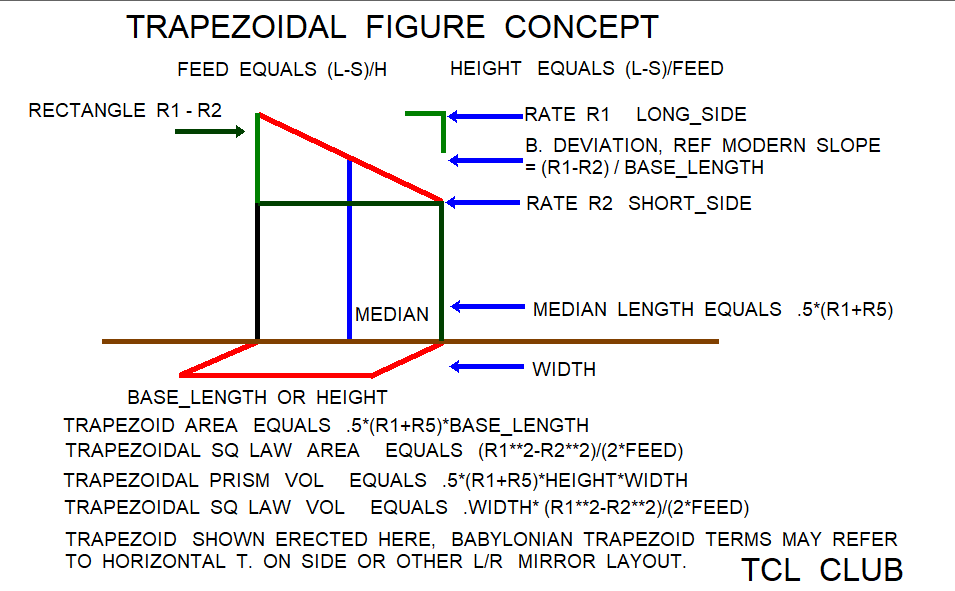
Babylonian Square Rule for Trapezoid Area
The Babylonian square rule for trapezoid area gives trapezoidal area = (l**2-s**2)/(2.*f), in conventional algebraic notation. In the TCL calculator, the Babylonian square rule for trapezoid area uses three given's as 1) parallel long_side length meters l, 2) parallel short_side length meters s, and 3) feed no units f. Most available tablets here suggest l > s as a condition where feed => 0 , but exceptions are possible. This paper refers to meters, square meters, and degrees to orient the modern user in problems compatible with modern textbooks. The feed parameter f = (l-s)/h. Rearranging terms, trapezoid height h = (l-s)/f. The Babylonian feed parameter for trapezoids may be defined as the rate or coefficient that for a given unit of height or depth (y), usually cubits, the horizontal distance (x) recedes N1 units. The Babylonian math problems dealt with trapezoids where the long and short parallel sides were either 1) horizontal, eg. 0 degrees) 2) vertical, eg. 90 degrees, or 3) in-between, eg. 45 degrees. If the long and short parallel sides of the trapezoid are horizontal, the feed parameter in the conventional and modern sense is equivalent to horizontal(r1-r2)/height(y) =oc x/y =oc inverse slope =oc cotangent (x/y). If the long and short parallel sides of the trapezoid are vertical, the feed parameter in the conventional and modern sense is equivalent to vertical(r1-r2)/horizontal(x) =oc y/x =oc slope =oc tangent (y/x). Also, the Babylonian square law for trapezoid area was extended to volumes by *width factor w. The trapezoid_area_sq_law gives trapezoidal volume = w*(l**2-s**2)/(2.*f).
Conventional Western Formula for Trapezoid Area
The Babylonian square rule for trapezoid area gives trapezoidal area = (l**2-s**2)/(2.*f), in conventional algebraic notation. following gives the conventional Western formulas used for trapezoidal area. The conventional trapezoid area is area2 = .5*(l+s)*h. The conventional median is median m1 = .5*(l+s). The conventional trapezoidal volume gives vol2 = .5*(l+s)*h*w.
For comparison of the Babylonian Square Rule with conventional formulas, TCL code will include redundant procs, calculation paths, and formulas to compute trapezoid area and volume.
Push Button Operation
For the push buttons, the recommended procedure is push a testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console. For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2)., TC(3), TC(4) etc. The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button.
Table, Math Terms Associated with Babylonian Trapezoids
| Table , Math Terms Associated with Babylonian Trapezoids | printed in tcl format | modern equivalent, English | comment if any | |
|---|---|---|---|---|
| sag ki.gu : | side earth | trapezoid | ||
| sag ki.ta : | side earth its , possessive case | upper front of the trapezoid | ||
| sag an.na : | side upper | upper front of the trapezoid | ||
| us gi.na : | length front | true length of the trapezoid | ||
| sag gi.na : | side front | true front of trapezoid | ||
| N1 kus i-ku-lu : | N1 cubit in eats it (it or man), read left to right | feed parameter of the trapezoid | noun derived from Sumerian SOV phrase | |
| sag du : | side | triangle | ||
| N1 arakarum : | N1 multiply | transformation coefficient, usually scale up |
Note. These Math Terms cover 4 or 5 cuneiform languages, and 5000 years of history. Math Terms are best understanding of context and math connotation here,not blessed by linguists and cuneiform dictionaries.
Testcases Section
Testcase 1
| table 1 | printed in | tcl format | |
|---|---|---|---|
| quantity | value | comment, if any | |
| 1: | testcase_number | ||
| 38.0 : | long_side length , meters: | ||
| 21.0 : | short_side length , meters: | ||
| 1.0625 : | feed rating: | ||
| 1.0 : | optional, default=1 , width meters: | ||
| 16.0 : | answers, height calculated, meters : | ||
| 29.5 : | conventional median, (l+s)/2, meters: | ||
| 1.0625 : | feed calculated: | ||
| 472.0 : | volume, width * B. sq law, meters cubed: | ||
| 472.0 : | conventional area formula, .5*(l+s)*h, meters squared: | ||
| 472.0 : | trapezoid area from square rule, meters squared: |
Testcase 2
| table 2 | printed in | tcl format | |
|---|---|---|---|
| quantity | value | comment, if any | |
| 2: | testcase_number | ||
| 18.0 : | long_side length , meters: | ||
| 6.0 : | short_side length , meters: | ||
| 1.330 : | feed rating: | ||
| 1.0 : | optional, default=1 , width meters: | ||
| 9.022 : | answers, height calculated, meters : | ||
| 12.0 : | conventional median, (l+s)/2, meters: | ||
| 1.329 : | feed calculated: | ||
| 108.270 : | volume, width * B. sq law, meters cubed: | ||
| 108.270 : | conventional area formula, .5*(l+s)*h, meters squared: | ||
| 108.270 : | trapezoid area from square rule, meters squared: |
---
Testcase 3
| table 3 | printed in | tcl format | |
|---|---|---|---|
| quantity | value | comment, if any | |
| 3: | testcase_number | ||
| 24.0 : | long_side length , meters: | ||
| 20.0 : | short_side length , meters: | ||
| 0.333 : | feed rating: | ||
| 1.0 : | optional, default=1 , width meters: | ||
| 12.012 : | answers, height calculated, meters : | ||
| 22.0 : | conventional median, (l+s)/2, meters: | ||
| 0.333 : | feed calculated: | ||
| 264.264 : | volume, width * B. sq law, meters cubed: | ||
| 264.264 : | conventional area formula, .5*(l+s)*h, meters squared: | ||
| 264.264 : | trapezoid area from square rule, meters squared: |
Screenshots Section
figure 1.

figure 2.

figure 3.
figure 4.
figure 5.
figure 6.
figure 7.
figure 8.
References:
- Amazing-Traces-of-a-Babylonian-Origin-in-Greek-Mathematics,
- Joran Friberg. Primary reference
- google < Babylonian trapezoid Wikipedia >
- Wikipedia search engine < trapezoid >
- Wikipedia search engine <mesopotamian unit measurement >
- Wolfram Alpha search engine < trapezoid >
- Ancient Babylonian Algorithms, Donald E. Knuth, Stanford University
- Category Algorithm
- A Remarkable Collection of Babylonian Mathematical Texts, Joran Friberg, 2007
- Chalmers University of Technology Gothenburg, Sweden
- Joran Friberg and andrew george,
- Six more mathematical cuneiform texts in the Schoyen collection, MS 3895,
- Amazing Traces of a Babylonian Origin in Greek Mathematics,
- Joran Friberg
- A Remarkable Collection of Babylonian Mathematical Texts:
- Manuscripts in the Schøyen Collection: Cuneiform Texts I},
- Joran Friberg
- Babylonian Mathematical Astronomy: Procedure Texts,
- by Mathieu Ossendrijver, trapezoids in astronomy
- measures Jupiter motion
Pseudocode & Equations Section
formulas
following includes algebraic expressions,
terms, and notation
Western trapezoid formulas
and trapezoidal prism volume
following includes algebraic expressions,
terms, and notation not used on tablets
side_aa refs top, t. on side
side_bb refs bottom, t. on side
side_cc refs height, t. on side
median_length = .5*(side_aa+side_bb)
trapezoid_area= 0.5*(side_aa+side_bb)*height
trapezoid_area= median*height
trapezoidal_prism_volume=
t. vol=length*(0.5*(side_aa+side_bb))*height
median divides equal side lengths
Equations reference
1) median = .5*(l+s) conventional
2) trapezoid area = .5*(l+s)*h conventional
3) feed = (l-s)/h trapezoid_area_sq_law
4) h = (l-s)/feed trapezoid_area_sq_law
5) trapezoid area = (l**2-s**2)/(2.*feed) trapezoid_area_sq_law
# Also, the B. square rule for trapezoid area
# was extended to volumes by *width factor.
6) trapezoidal volume = .5*(l+s)*h*w conventional
7) trapezoidal volume = w*(l**2-s**2)/(2.*feed) trapezoid_area_sq_law
# end of file, pseudocode:Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# Babylonian Trapezoid Area V2
# written on Windows XP on TCL
# working under TCL version 8.6
# gold on TCL Club, 4oct2018
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {long_side length , meters:} }
lappend names {short_side length , meters:}
lappend names {feed rating: }
lappend names {optional, default=1 , width meters: }
lappend names {answers, height calculated :}
lappend names {conventional median, (l+s)/2, meters::}
lappend names {conventional area formula, .5*(l+s)*h, meters squared: }
lappend names {trapezoid area from square rule, meters squared:}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Babylonian Trapezoid Area V2
from TCL ,
# gold on TCL Club, 10aug2018 "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg "Calculator for Babylonian Trapezoid Area V2
from TCL ,
# self help listing
# 3 givens follow.
1) long_side length meters
2) short_side length meters
3) feed, B. parameter related oc modern slant or slope
4) optional height meters
The solution from the clay tablets
is genuine antique method from 1600 BCE
and different looking from modern math methods.
# The Babylonians did not use modern algebraic notation,
# so the reader will have to bear some anachronisms in the TCL code.
# Comparing conventional formula(s) for trapezoid area
# to Babylonian square rule for trapezoid area.
# For comparision, code will include redundant paths & formulas
# to compute trapezoid area. The calculator uses modern
# units as meters for convenience to modern users and textbooks.
# Any convenient and consistent in/output units might be used
# like inches, feet, nindas, cubits, or dollars to donuts.
# Equations
1) median = .5*(l+s) conventional
2) trapezoid area = .5*(l+s)*h conventional
3) feed = (l-s)/h trapezoid_area_sq_law
4) h = (l-s)/f trapezoid_area_sq_law
5) trapezoid area = (l**2-s**2)/(2.*feed) trapezoid_area_sq_law
# Also, the B. square rule for trapezoid area
# was extended to volumes by *width.
6) trapezoidal volume = .5*(l+s)*h*w conventional
7) trapezoidal volume = w*(l**2-s**2)/(2.*feed) trapezoid_area_sq_law
# Recommended procedure is push testcase and fill frame,
# change first three entries etc, push solve,
# and then push report. Report allows copy and paste
# from console to conventional texteditor. For testcases
# testcase number is internal to the calculator and
# will not be printed until the report button is pushed
# for the current result numbers.
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK 8.6 license terms.
# Editorial rights retained under the TCL/TK license terms
# and will be defended as necessary in court.
Conventional text editor formulas or grabbed from internet
screens can be pasted into green console.
Try copy and paste following into green screen console
set answer [* 1. 2. 3. 4. 5. ]
returns 120
# gold on TCL Club, 10aug2018 "
tk_messageBox -title "About" -message $msg }
proc trapezoid_solution { long_side short_side feed width} {
global trapezoid_area height_calc feed_calc median trapezoidal_vol
set median [* .5 [+ $long_side $short_side ]]
set height_calc [/ [- $long_side $short_side] $feed ]
set trapezoid_area [/ [- [* $long_side $long_side] [* $short_side $short_side] ] [* 2. $feed ] ]
set trapezoidal_vol [* $width [/ [- [* $long_side $long_side] [* $short_side $short_side] ] [* 2. $feed ] ]]
set feed_calc [ expr { ($long_side-$short_side)/ $height_calc } ]
puts " check $long_side $short_side $feed height_calc= $height_calc area= $trapezoid_area feed= $feed_calc "
return $trapezoid_area }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
global trapezoid_area height_calc feed_calc median trapezoidal_vol
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set side5 1
set side6 1
set side7 1
set side8 1
set long_side $side1
set short_side $side2
set feed $side3
set width $side4
# height_calc calculated from feed and sides,
# default for width equals 1.
set trapezoid_area_sq_law [ trapezoid_solution $side1 $side2 $side3 $side4 ]
set trapezoid_area_conventional [ expr { .5*($long_side+$short_side)* $height_calc } ]
set side5 $height_calc
set side6 $feed_calc
set side7 $trapezoid_area_conventional
set side8 $trapezoid_area_sq_law
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
global trapezoid_area height_calc feed_calc median trapezoidal_vol
console show;
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Babylonian Trapezoid Area V2 Report , screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts "%|table $testcase_number|printed in| tcl format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |&"
puts "&| $side1 :|long_side length , meters: | |&"
puts "&| $side2 :|short_side length , meters: | |& "
puts "&| $side3 :|feed rating: | |& "
puts "&| $side4 :|optional, default=1 , width meters:| | |&"
puts "&| $side5 :|answers, height calculated, meters :| | |&"
puts "&| $median :|conventional median, (l+s)/2, meters:| | |&"
puts "&| $side6 :|feed calculated:| | |&"
puts "&| $trapezoidal_vol :| volume, width * B. sq law, meters cubed:| | |&"
puts "&| $side7 :|conventional area formula, .5*(l+s)*h, meters squared:| | |&"
puts "&| $side8 :|trapezoid area from square rule, meters squared: | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 38.0 21.0 1.0625 1. 16. 1.0625 472. 472.}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 18.0 6.0 1.33 1. 1.0 1.333 108. 108. }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 24.0 20. 0.333 1. 1.0 0.333 264. 264. }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .self_help -text self_help -command {self_help}
::ttk::button .console2 -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .console2 .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Babylonian Trapezoid Area V2"
# gold on TCL Club, 4oct2018
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK 8.6 license terms.
# Editorial rights retained under the TCL/TK license terms
# and will be defended as necessary in court.
# end of fileappendix, procs for Tablet VAT_7848
# Tablet VAT_7848, published in MCT, Seleucid t. circa 300 BCE
# numbers from trapezoid problem in VAT_7848
# VAT_7848 uses version of Pythagorean theorem
# Numbers for isoceles trapezoid, not sure if formula
# works for all cases. ?cases of acute and right angle traps?
# both slant sides r3=30
# short parallel side s= 14
# long parallel side l= 50
# height h=24
# trapezoid_area = 768
# check formulas for trapezoid
set trapezoid_height2 [ expr { sqrt ( 30**2- ((50-14)/2.)**2 ) } ]
# square terms = expr sqrt(576), height = 24
set trapezoid_area2 [ expr 24.*((50-14)/2.) ] # answer = 768.
# develop TCL procs
proc trapezoid_height { l s r3 } {return [ expr { sqrt ( $r3**2- (($l-$s)/2.)**2 ) } ] }
proc trapezoid_area {s l h} {return [ expr { $h*(($l+$s)/2.) } ] }
trapezoid_height 30. 50. 14. # answer = 24
trapezoid_area 50. 14. 24. # answer = 768
# end of fileappendix, Calculations for another Tablet DPA34
# Tablet DPA34, pub Friberg,
# Old Akkadian period (c. 2340-2200 BC)
# example: field expansion procedure (algorithm)
# example: trapezoid field problem
# probably task was calc area and converting
# to regular “almost round” units of area.
# school problem on near trap. field
# dimensions in 3 lines as follows.
# 26 nindas north 110 nindas east
# 58 nindas south 106? nindas west
# (given area) 2 bur 1 ese 3 iku (cuneiform units of area)
# note: answer and solution method not supplied on tablet.
# Answer above equivalent to
# expr 2*1800+1*6*100+3*100 = 4500 nindas
# Not on the tablet, but a check answer could be
# computed from the approximate quadrilateral formula.
# Opposite sides are a&c,b&d, but formula not exact
# condition {a b c d} > 0
proc approx_quadrilateral_area { a b c d } {
return [ expr { (($a+$c)/2.)*(($b+$d)/2.) } ]
}
set field area [ approx_quadrilateral_area 26 110 58 106 ]
# proc answer 4536??? decimal nindas, problems in agreement
# online internet calc answer = 4480.86
# online cyclic quadrilateral = 4480.8570
# Strangely, average expr (4536+4480)/2=4508.0 is
# right on the money.
# end of fileappendix, Calculations for another Tablet W20044
# Tablet W20044, pub CDLI, Friberg & D.A.R. DeSegnac,
# Archaic period (c. (3350 to 3200 BCE)
# example: field expansion procedure (algorithm)
# example: trapezoid (algorithm)
# probably task was calculating area and converting
# to regular “almost round” units of area.
# school problem on near trap. field
# dimensions in 4 slots as follows.
# 75 nindas (north?, | stroke)
# 100 nindas (east?, - stroke)
# 60 nindas (south?, | stroke )
# 120 nindas (west?, - stroke)
# Not on the tablet,
# ( area book answer) is 7425 square nindas
# 7425 square nindas conv. 4 burs and 2 iku (units of area)
# area = 4*1800+2*100 = 7400 square nindas
# Not on the tablet, but a check answer could be
# computed from the cyclic quadrilateral formula.
set field_area1 [ approx_quadrilateral_area 26 110 58 106 ]
# proc answer 7325.978 decimal nindas, 4 burs.
# quadrilateral broken into 2 right triangles.
# ajacent sides used
set field_area2 expr 60*100*.5+120*75*.5
# 7500.0 = = 4 burs 3 iku.
approximate quad = expr ((75.+60.)/2.)* ((100.+120.)/2.)
# 7425.0, gives 4 burs 2 iku rounded
# 60*60 sq. nindas = 2 bur, 1 bur = 1800 sq ninda
# Friberg shows area from approx. formula was
# expr {7425-4*1800} # or 225 sq. n. over a whole number in 4 burs.
# 7425/(4*1800.) = 1.03125 decimal over whole number (1).
# Field expansion procedure algorithm as square of (side+1/60),
# (side+1/60 fraction)+(side+1/60 fraction)=
expr { (1+1/60.)*(1+1/60) } = 1.0336 decimal
# is close to result.
# Also, a sqrt of expr (4*1800)**.5 = 84.852 decimal or 84+51/60
# test square of same area = 84.8*84.8=7191 sq nindas
# test square of same area, 84.8, on side,
# expr { (84.8+84.8*1/60.)*(84.8+84.8*1/60.) }= 7432.73
average long side = expr (120+100)/2. = 110.0
average long side = expr (60+75)/2. = 67.5
average ratio of average sides expr ((120+100)/2.)/( (60+75)/2.)=1.629
The golden mean is expr (1. +sqrt(5))/2 = 1.61803
short avg over long avg is expr ((60+75)/2.)/ ((120+100)/2.)= 0.6136
expr 1./((1. +sqrt(5))/2.)= 0.61803
This is the earliest documented example of Golden Mean that
has been found, in Archaic period (c. (3350 to 3200 BCE).
In base_60 and rounded to near 1/60 (B. regular number), the Golden Mean
or Golden Ratio would be expr { 1+ .61803*60} or 1+37/60.
The Golden Ratio Conjugate = expr {1/1.61803} = .61803 or 37/60.
# end of fileappendix, Calculations for another Tablet W 19408_76+
# Tablet W 19408_76+, pub CDLI, Friberg, & D.A.R. DeSegnac,
# Archaic period (c. (3350 to 3200 BCE)
# example: trapezoid (algorithms)
# probably task was calculating area and converting
# to regular “almost round” units of area.
# school problem on near trap. field
# dimensions in 4 slots as follows.
# units 60*60 square nindas = 2 bur, 1 bur = 1800 sq ninda
# 1280 nindas from expr { 2*600+1*60+2*10 } ( | slash , north? )
# 990 nindas expr { 1*600+6*60+3*10 } ( ____ slash , east? )
# 520 nindas from expr { 8*60+4*10 } ( | slash , south?)
# 1410 from expr { 2*600+ 3*60+3*10 } ( ____ slash west?)
# Area answer not on the tablet, but a check answer could be
# computed from the cyclic quadrilateral formula.
# ( area round number) is 1080000.0 square nindas or 600 burs
# t. area 996142.580 sq nindas from cyclic_quadrilateral_area 1280 990 520 1410
# c.q. approx 996142/1800 or 553 burs, prob. intended 600 burs.
# area = 1080000.0 approx_quadrilateral_area 1280 990 520 1410
# expr {600*1800} = 1080000 square nindas
# ratio of averages for opposite sides.
# 1.333 or 80/60 from expr { ( .5* (990+1410))/(.5*(1280+ 520)) }
# Note. 600 burs was relatively huge and unrealistic grain field
# for a city state. Each plow team was assigned 3 burs to plow
# over ten day period.
# The field of 600 burs would require expr {600/3} or 200 plow teams.
# The city of Umma in the classic URIII period required not more than
# 60 plow teams for 233.28 sq km of state land.
# Equivalent square side was expr {sqrt (1080000)} or 1039 nindas
# end of fileappendix, Golden Rectangle Dimensions for even numbered area units (burs)
golden rectangle ratio for 2 bur units
short_side_S*long_side_L = 2 bur in golden rectangle ratio
(1*S)*(1.61803*S)=expr 2*1800 # 4 bur
1.61803*(S**2)=3600 sq nindas
S**2= expr { 3600./1.61803 }
set S [expr { sqrt (2224.927) }]
S=47.169, L = 76.321 from expr { 1.61803*47.169}
check expr {47.169*76.321 } = 3599.985 square nindas golden rectangle ratio for 4 bur units
short_side_S*long_side_L = 4 bur in golden rectangle ratio
(1*S)*(1.61803*S)=expr 4*1800 # 4 bur
1.61803*(S**2)=7200 sq nindas
S**2= expr { 7200./1.61803 }
set S [expr { sqrt 4449.855 }]
S=66.7, L = 107.922 from expr { 1.61803*66.7}
check expr {66.7*107.922 } = 7198.3974 square nindasgold This page is copyrighted under the TCL/TK license terms, this license .
Hidden Comments Section
** Hidden Comments Section **
Please place any comments here with your moniker, Thanks.
test! seems to work
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |