Binomial Probability Slot Calculator Example

This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 12Dec2018

Introduction

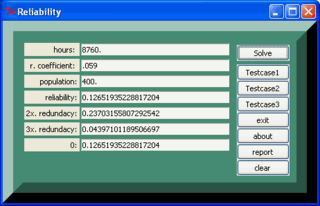
gold Here is some starter code for Binomial Probability Slot Calculator Example. The impetus for this calculator was checking some iching probabilities on the Chinese Iching Random Weather Predictions. Its easy enough to plug in two formulas into the Slot_Calculator_Demo example. Most of the checked testcases involve flipping two sided objects like coins or popsicle sticks.

In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Also, some of the pseudocode statements were checked in the google search engine which will take math expressions. The factorial procedure used below was posted by Suchenworth. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the binomial function. and the factorial (fact) function.

For a system of 2 sided sticks or coins of the number N, the probability of getting all zeros or ones would be:

 set aa [ expr { (1./(2**$N))} ] ;# generic TCL

For three coins, the formula would be 1/(2**3) or 1/8.

 set aa [ expr { (1./(2**3)} ]

For six coins, the formula would be 1./(2**6) or 1/64

 set aa [ expr { (1./(2**6)} ]

For N coins, the probability that a one or zero would show up on one of N coins would be

 set aa [ expr { (1.-(1./(2**$N)))} ]

Testcase 1

The testcase 1 was 6 choose 2. The sample size was 2**6 or 64.

 set gg [ expr { 2**6 } ]

The probabliity of getting all heads or all tails from 6 coins was 1/(2**6) or 1/64.

 set rr [ expr { 1./(2**6) } ]

The answer for 6 coins choose 2 was 0.234

Testcase 2

The testcase 2 was 3 choose 2. The sample size was 2**3 or 8.

 set kk [ expr { 2**3 } ]

The probability of getting all heads or all tails from 3 coins was 1/(2**3) or 1/8.

 set jj [ expr { 1./(2**3) } ]

The answer for 3 coins choose 2 was 0.375.

Testcase 3

The testcase 3 was 12 choose 2. The sample size was 2**10 or 4096.

 set xx [ expr { 2**12 } ]

The probabliity of getting all heads or all tails from 12 coins was 1/(2**12) or 1/4096 or 2.441E-4

 set vv [ expr { 1./(2**12) } ]

The answer for 12 choose 2 was 0.01611.

Session from console

    1% set rr [ expr { 1./(2**12) } ]
      0.000244140625
    2% set gg [ expr { 2**12 } ]
    4096
    3% set rr [ expr { 1./(2**6) } ]
    0.015625
    4% set gg [ expr { 2**6 } ]
    64

Testcase 4

The testcase 4 was 4 coins choose 2. The sample size was 2**4 or 16.

 set xx [ expr { 2**4 } ]

The probabliity of getting all heads or all tails. from 4 coins was 1/(2**4) or 1/16 or .0625

 set vv [ expr { 1./(2**4) } ]

The answer for 4 coins choose 2 was 0.375.

Testcase 5

The testcase 5 was 9 coins choose 2. The sample size was 2**9 or 512.

 set xx [ expr { 2**9 } ]

The probabliity of getting all heads or all tails from 9 coins was 1/(2**9) or 1/512 or .00195

 set vv [ expr { 1./(2**9) } ]

The answer for 9 coins choose 2 was 0.0703

Console session

    1% set xx [ expr { 2**4 } ]
    16
    2% set vv [ expr { 1./(2**4) } ]
    0.0625
    3% binom 4 2 2
    0.375
    4% set xx [ expr { 2**9 } ]
    512
    5% set vv [ expr { 1./(2**9) } ]
    0.001953125
    6% binom 9 2 2
    0.07031251
    % fact 9
      362880

Testcase 6

The testcase 6 was 20 coins choose 10. The sample size was 2**20 or 1,048,576.

 set zz [ expr { 2**20 } ]

The probabliity of getting all heads or all tails from 20 coins was 1/(2**20) or 1/1,048,576 or 9.536E-7.

 set xx [ expr { 1./(2**20) } ]

The answer for 20 coins choose 10 was 0.1762.

Testcase 7

The testcase 7 was 100 coins choose 50. The sample size was 2**100 or 1.26765E+30. google(2 ** 100) = 1.2676506 × 10E30

  set zz [ expr { 2**100 } ]

The probabliity of getting all heads or all tails from 20 coins was 1/(2**100) or 1/1.26765E+30 or 7.888609E-31. google(1 / (2 ** 100)) = 7.88860905 × 10-31.

 set xx [ expr { 1./(2**100) } ]

The answer for 100 coins choose 50 was 0.013843748310702326.

Console session compared to stattrek.com

    2% binom 100 50 2
    0.07978845608028655           stattrek( 0.0795892373871788 )     
    3%  binom 100 60 2
    0.010872519679731506          stattrek(0.010843866711638)   
    4% binom 100 70 2
    2.3243440318642605e-5         stattrek( 2.31706905801352E-05 )      
    5% binom 100 80 2 
    4.229044215516387e-10         stattrek( 4.22816326760158E-10 )   
    6% binom 100 90 2  
    1.3656690823232337e-17        stattrek( 1.36554263874631E-17)
    7% binom 100 95 2  
    5.939398609386625e-23         stattrek( 5.93913811790451E-23)
    8% binom 100 99 2
    7.888675454251962e-29         stattrek(7.88860905221012E-29)

Testcase 8

The testcase 8 was 120 coins choose 50.1.329227E+36. The sample size was 2**120 or 1.329227E+36. google(2 ** 120) = 1.329228 × 10E36

 set zz [ expr { 2**120 } ]

The probability of getting all heads or all tails from 120 coins was 1/(2**120) or 1/ 1.329227E+36 or 7.5231E-37 google(1 / (2 ** 120)) = 7.52316385 × 10-37

 set xx [ expr { 1./(2**120) } ]

The answer for 120 coins choose 50 was 0.013843748310702326, omparable to stattrek(0.0138138412069122).

     #console session 
     12% binom 120 50 2
     0.013843748310702326

Extra Credit

For a system of one die with kk sides of the number N tosses, the sample size would be:

 set aa [ expr { ($kk**$N)} ]

For example, a 6 sided die with 2 tosses would have a sample size of 6**2 or 36.

 set aa [ expr { ( 6**2 )} ]

The probability of two dice having the same face like snake eyes (1:1) on one throw is 1/(sample size) or 1/36.

 set pp [ expr { 1./(6**2) } ]

The following sums the numbers on two faces. For 2 dice of 6 sides, the probability of a number 7 coming up is 0.1666. In pseudocode statements, the probability of two dice landing with sum 7 would be the number of combinations that add up to seven over the number of all possible combinations from throwing 2 dice. Such a $list can generated in the auxillary eTCL script at the bottom of page.

   prob. pseudocode   = nom ($list) / denom ( $list) 
   prob. pseudocode
   = llength [lsearch -all $list 7 ] / [llength $list ]
   prob. pseudocode
   = [llength [lsearch -all $list 7 ]] / [llength $list ]

This would find our probability of throw 7 on a one time basis. For the calculator, this process could be generalized into a subroutine that generated a list for 2 to N sides: list(N), an expected dice throw as $facenumber, counted the number of throws showing $facenumber in list(N), and counted all the elements in the list(N).

  prob. pseudocode   = 
  [llength [lsearch -all $list(N) $facenumber ]] / [llength $list(N) ]

Also, another foreach loop in the list generator could probably generate the possible throws of three dice.

Screenshots Section

test reload of images from offsite

Screenshots Section

figure 1.

figure 2.

figure 3.

figure 4.

figure 5.

figure 6.

References

factorial
Slot_Calculator_Demo
http://www.knowyourluck.com/coins3u.html (currently 404)
http://www.learning.com/pdfs/et/activity-35-cointoss.pdf
http://stattrek.com/Tables/Binomial.aspx Binomial Distribution Calculator
Sample Math Programs modified [PSE} operation tables to generate throw do-loops
http://hyperphysics.phy-astr.gsu.edu/hbase/math/dice.html Statistics of Dice Throw
http://wizardofodds.com/gambling/dice.html Dice Probability basics
http://www.cobalt.chem.ucalgary.ca/ziegler/educmat/chm386/rudiment/mathbas/probab.htm Probability
http://gwydir.demon.co.uk/jo/probability/calcinfo.htm Calculating probabilities of throwing two dice
Math Forum,Date: 05/16/99, Doctor Anthony,Probability dealing with combinations of dice
Math Forum,Doctor Jeremiah,Probability of dicehttps://wiki.tcl-lang.org/13243
Google Answers Probability of Coin Flip.mht
2 Dice Rolls Probability-Statistics -
Doctor Math,[L1 ]

appendix TCL programs

Pretty Print Version

    # Pretty Print version from autoindent and ased editor
    # written on Windows XP on eTCL
    # working under TCL version 8.5.6 and eTCL 1.0.1
    # gold on TCL WIKI , 21Jul2010
  package require Tk
    frame .frame -relief flat -bg aquamarine4
    pack .frame -side top -fill y -anchor center
    
    set names {{} N_coins: heads: {sides:} {sample:} {1/sample:} {answer:} 1/sample:}
    foreach i {1 2 3 4 5 6 } {
        label .frame.label$i -text [lindex $names $i] -anchor e
        entry .frame.entry$i -width 35 -textvariable side$i
        grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1
    }
    proc about {} {
        set msg "Calculator for binomial probabliity.
        from TCL WIKI,
        written on eTCL "
        
        tk_messageBox -title "About" -message $msg
    }
    proc pi {} {expr acos(-1)}
    
    proc fact n {expr {
            
            $n<2? 1:
            $n>20? pow($n,$n)*exp(-$n)*sqrt(2*acos(-1)*$n):
            wide($n)*[fact [incr n -1]]}
    }
    
    proc binomialprobabilty { aa  bb  cc dd  ee   } {
        
        #set aa 6
        #set bb 4
        #set cc 2
        set sidex $cc
        set aa [ expr { int($aa) } ]
        set cc [ expr { int($bb) } ]
        set bb [ expr { $aa-$cc } ]
        
        set term1 [ fact $aa ]
        set term2 [ fact $bb ]
        set term3 [ fact $cc ]
        
        set sample [ expr { $sidex**$aa} ]
        set binprob [ expr { ($term1*1.)/($term2*$term3*$sample*1.)  } ]
        
        return  $binprob  ;
        
    }
    
    proc binom { aa  bb  cc    } {
        
        #set aa 6
        #set bb 4
        #set cc 2
        set sidex $cc
        set aa [ expr { int($aa) } ]
        set cc [ expr { int($bb) } ]
        set bb [ expr { ($aa-$cc) } ]
        set term1 [ fact $aa ]
        set term2 [ fact $bb ]
        set term3 [ fact $cc ]
        
        set sample [ expr { $sidex**$aa} ]
        set binprob [ expr { ($term1*1.)/($term2*$term3*$sample*1.)  } ]
        
        return  $binprob  ;
        
    }
    
    proc pol { xx1 yy1 xx3 yy3 xx2   } {
        return [expr {  ((($xx2-$xx1)*($yy3-$yy1))/($xx3-$xx1))+ $yy1 } ] ;}
    
    proc calculate {     } {
        global answer2  
        global side1 side2 side3 side4 side5 side6
        set answer2  [ binomialprobabilty  $side1 $side2 $side3 $side4 $side5  ]
        set side4 [ expr { $side3**$side1     } ]
        set side5 [ expr { 1./ ($side3**$side1)     } ]
        set side6 $answer2
        
        set pi5 [pi]
        if {$answer2 >= $pi5} { set error5   [expr {100.*$answer2/$pi5-100.}]   }
        if {$answer2 <= $pi5} { set error5   [expr {100.*$pi5/$answer2-100.}]   }
        #$x insert 1.0 " % error $error5 "
        #$t insert 1.0 " % error  $error5 "
        
    }
    proc fillup {aa bb cc dd ee ff } {
        
        .frame.entry1 insert 0 "$aa"
        .frame.entry2 insert 0 "$bb"
        .frame.entry3 insert 0 "$cc"
        .frame.entry4 insert 0 "$dd"
        .frame.entry5 insert 0 "$ee"
        .frame.entry6 insert 0 "$ff "
        
    }
    proc clearx {} {
        foreach i {1 2 3 4 5 6 } {
            .frame.entry$i delete 0 end
        }
    }
    
    proc reportx {} {
        console show;
        puts "
        The binom function takes
        three  quantities.
        The points are aa,bb ,cc.
        The input order of the 3 items
        is  N_coins heads sides
        and solving for binomial probability.
        eg. binom 9 2 2 gives 0.0703
        "
    }
    
    frame .buttons -bg aquamarine4
    
    ::ttk::button .calculator -text "Solve" -command { calculate   }
    
    ::ttk::button .test2 -text "Testcase1" -command { clearx;fillup 6. 2. 2. 64.  .0156 .234375 }
    ::ttk::button .test3 -text "Testcase2" -command { clearx;fillup  3. 2. 2. 8.  .125 .375 }
    ::ttk::button .test4 -text "Testcase3" -command { clearx;fillup 12. 2. 2. 4096.  2.4E-4 .01611 }
    ::ttk::button .clearallx -text clear -command {clearx  }
    ::ttk::button .about -text about -command about
    ::ttk::button .cons -text report -command { reportx }
    ::ttk::button .exit -text exit -command {exit}
    pack .calculator  -in .buttons -side top -padx 10 -pady 5
    
    pack  .clearallx .cons .about .exit .test4 .test3  .test2   -side bottom -in .buttons
    grid .frame .buttons -sticky ns -pady {0 10}
    . configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
    wm title . "Binomial Probablity Slot Calculator Example "

*Auxillary programs

Here's searching through a list of thrown dice combos for probability. The worker bee is

 [ lsearch -all [ listofnn $nn ] $facen ]
 $facen is the sum of a 2-dice throw like 7.
 $nn is the number of sides,eg 6.

Subroutine is invoked by a foreach procedure for probability, which would be number of thrown 7's over all possible throws. Drop (-all) and lose all, returning only one position of "7" in list.

Console program for two 6-sided dice

      # prob. subroutines for two 6-sided dice
      # throw of 7 etc.
      proc listofnn { nn } {
      set lister [list ]
      for { set i 1 } { $i <= $nn }  { incr i } {
          lappend lister $i
      }
      set i 0
      while { [ incr i ] <= $nn } {
         foreach item $lister {
            append listofnn " [ expr {$item+$i} ]"
         }
 
      }
     return $listofnn
      }
     proc calculation { nn  facen }  {   
     set ee [llength [ listofnn $nn ]]
     set kk [ llength [ lsearch -all [ listofnn $nn ] $facen ] ]
     set prob [ expr { ($kk*1.) / $ee  } ]
     return $prob
     }
    console show
          set limit 12
          for { set i 1 } { $i <= $limit }  { incr i } {
          lappend listxxx $i 
          lappend listxxx [ calculation 6 $i ]
          puts " $i [ calculation 6 $i ] "
          }
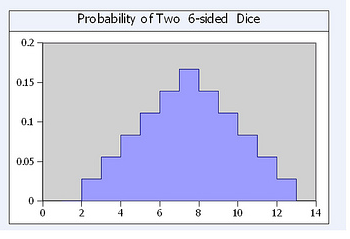
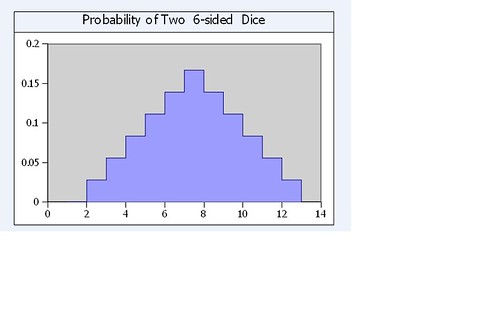
     puts $listxxx

Output for plot

output plotted in jpg above

 1 0.0 
 2 0.027777777777777776 
 3 0.05555555555555555 
 4 0.08333333333333333 
 5 0.1111111111111111 
 6 0.1388888888888889 
 7 0.16666666666666666 
 8 0.1388888888888889 
 9 0.1111111111111111 
 10 0.08333333333333333 
 11 0.05555555555555555 
 12 0.027777777777777776 
    #end

Console program for two 6-sided dice

     # written on Windowws XP on eTCL 
     # working under TCL version 8.5.6 and eTCL 1.0.1 
     # gold on TCL WIKI , 21Jul2010
     # find probability of 7 on 2 6-sided dice.

      proc listofnn { nn } {
      set lister [list ]
      for { set i 1 } { $i <= $nn }  { incr i } {
          lappend lister $i
      }
      set i 0
      #puts $lister
      while { [ incr i ] <= $nn } {
         foreach item $lister {
            append listofnn " [ expr {$item+$i} ]"
         }
 
      }
     return $listofnn
 }

Pseudocode program for two dice

    console show
    #not efficient code here.
    #trying to show evolution
    #from pseudocode
    puts " prob. pseudocode   = nom (\$list) \/ denom ( \$list) "
    puts "pseudocode:find all possible combinations from throwing 2 dice"
    puts [ listofnn 6 ]
    puts "pseudocode: find length of list"
    puts "pseudocode:\[llength \$list \]"
    puts [llength [ listofnn 6 ]]
    set ee [llength [ listofnn 6 ]]
    puts "pseudocode: find positions of 7 in list"
    puts "prob. pseudocode   \= \[lsearch -all \$list 7 \] "
    puts [ lsearch -all [ listofnn 6 ] 7 ]
    puts "pseudocode: count number of throws of 7"
    puts " prob. pseudocode   \= llength \[lsearch -all \$list 7 \] "
    puts [ llength [ lsearch -all [ listofnn 6 ] 7 ] ]
    set kk [ llength [ lsearch -all [ listofnn 6 ] 7 ] ]
     puts "prob. pseudocode   = \[llength \[lsearch -all \$list 7 \]\] \/ \[llength \$list \]"
    #not efficient code here.
    #trying to show evolution
    #from pseudocode
    set prob [ expr { ($kk*1.) / $ee  } ]
    puts $prob
    #end of deck

Pseudocode for finding positions of 7 in sequence

   printed output of deck
  prob. pseudocode   = nom ($list) / denom ( $list) 
  pseudocode:find all possible combinations from throwing 2 dice
   2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 7 8 9 5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12
  pseudocode: find length of list
  pseudocode:[llength $list ]
  36
  pseudocode: find positions of 7 in list
  prob. pseudocode   = [lsearch -all $list 7 ] 
  5 10 15 20 25 30
  pseudocode: count number of throws of 7
  prob. pseudocode   = llength [lsearch -all $list 7 ] 
  6
  prob. pseudocode   = [llength [lsearch -all $list 7 ]] / [llength $list ]
  0.16666666666666666

eTCL program

     # written on Windowws XP on eTCL 
     # working under TCL version 8.5.6 and eTCL 1.0.1 
     # gold on TCL WIKI , 21Jul2010
     frame .frame -relief flat -bg aquamarine4
      pack .frame -side top -fill y -anchor center

    set names {{} {throw:} {N_sides:} {No_dice:} {sample:} {1/sample:} {answer:} 1/sample:}
   foreach i {1 2 3 4 5 6 } {
    label .frame.label$i -text [lindex $names $i] -anchor e
    entry .frame.entry$i -width 35 -textvariable side$i
    grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1
     }
  proc about {} {
    set msg "Calculator for Probablity N-sided Double Dice.
          from TCL WIKI,
          written on eTCL "
    
    tk_messageBox -title "About" -message $msg
 }
     proc pi {} {expr acos(-1)}

     proc fact n {expr {
    
     $n<2? 1:
     $n>20? pow($n,$n)*exp(-$n)*sqrt(2*acos(-1)*$n):
            wide($n)*[fact [incr n -1]]}
     }

      proc listofnn { nn } {
      # prob. subroutines for two 6-sided dice
      # throw of 7 etc.
      
      for { set i 1 } { $i <= $nn }  { incr i } {
          lappend lister $i
      }
      set i 0
      while { [ incr i ] <= $nn } {
         foreach item $lister {
            append listofnn " [ expr {$item+$i} ]"
         }
 
      }
     return $listofnn
      }
     proc dice { facen nn   }  { 
     # prob. subroutines for two 6-sided dice
     # throw of 7 etc.
       set facen [ expr { int($facen) } ] 
       set nn [ expr { int($nn) } ] 
     set ee [llength [ listofnn $nn ]]
     
     set kk [ llength [ lsearch -all [ listofnn $nn ] $facen ] ]
     set prob [ expr { ($kk*1.) / ($ee*1.)  } ]
     return $prob
     }

  proc binom { aa  bb  cc    } {

      #set aa 6
      #set bb 4
      #set cc 2
       set sidex $cc
       set aa [ expr { int($aa) } ] 
       set cc [ expr { int($bb) } ] 
       set bb [ expr { ($aa-$cc) } ] 
      set term1 [ fact $aa ]
      set term2 [ fact $bb ]
      set term3 [ fact $cc ]

      set sample [ expr { $sidex**$aa} ]
      
      set binprob [ expr { ($term1*1.)/($term2*$term3*$sample*1.)  } ]

     return  $binprob  ;

     }

    proc pol { xx1 yy1 xx3 yy3 xx2   } {
     return [expr {  ((($xx2-$xx1)*($yy3-$yy1))/($xx3-$xx1))+ $yy1 } ] ;}

    proc calculate {     } {
    global colorwarning
    global colorback
    global answer2   answer3
    global side1 side2 side3 side4 side5 side6 
       set answer2 ""
   
   set side3 [ expr { int($side3)     } ]
   set answer2  [dice  $side1 $side2  ] 
   
   set side4 [ expr { $side2**$side3     } ]
   set side5 [ expr { 1./ ($side2**$side3)     } ]
   set side6 $answer2  
   
      set pi5 [pi]
   if {$answer2 >= $pi5} { set error5   [expr {100.*$answer2/$pi5-100.}]   }
   if {$answer2 <= $pi5} { set error5   [expr {100.*$pi5/$answer2-100.}]   }
   #$x insert 1.0 " % error $error5 " 
   #$t insert 1.0 " % error  $error5 "

      }
      proc fillup {aa bb cc dd ee ff } {
    
    .frame.entry1 insert 0 "$aa"
    .frame.entry2 insert 0 "$bb"
    .frame.entry3 insert 0 "$cc"
    .frame.entry4 insert 0 "$dd"
    .frame.entry5 insert 0 "$ee"
    .frame.entry6 insert 0 "$ff "
   
      }

      proc clearx {} {
    foreach i {1 2 3 4 5 6 } {
        .frame.entry$i delete 0 end
    }
    }

   proc reportx {} { 
   console show;
   puts "
   The interpolation function takes 
   two know points on a line and
   solves for an intermediate point.
   The points are xx1,yy1,xx2,yy2 and xx3,?yy3?
   The interpolation function loaded as
   proc pol. User should be able 
   to cut and paste (c&p)
   pol 50. 1000. 200. 1200.  150.
   and save answer (1133.3)  on console.
   ********
   The binom function takes 
   three  quantities.
   The input order of the 3 items
   is  N_coins heads sides.  
   and solving for binomial probability.
   eg. (c&p) binom 9 2 2 gives 0.0703
   *********
   The listofnn function 
   returns a list of combos for
   N_sides double dice.
   Max combo should be twice N_sides.
   eg. (c&p) listofnn 6 gives 36 combos
   ************
   The dice function takes 
   two  quantities.
   The input order of the 2 items
   is  throw N_sides.  
   eg.(c&p) dice 7 6 gives 0.166
    "

    }

  frame .buttons -bg aquamarine4
    
    ::ttk::button .calculator -text "Solve" -command { calculate   }

    ::ttk::button .test2 -text "Testcase1" -command { clearx;fillup 7. 6. 2. 36.  .0277 .166 }
    ::ttk::button .test3 -text "Testcase2" -command { clearx;fillup 3. 6. 2. 36.  .0277 .0555 }
    ::ttk::button .test4 -text "Testcase3" -command { clearx;fillup 2. 6. 2. 36.  .0277 .0277 }
    ::ttk::button .clearallx -text clear -command {clearx  }
    ::ttk::button .about -text about -command about
    ::ttk::button .cons -text report -command { reportx }
    ::ttk::button .exit -text exit -command {exit}
    pack .calculator  -in .buttons -side top -padx 10 -pady 5
     
    pack  .clearallx .cons .about .exit .test4 .test3  .test2   -side bottom -in .buttons
    grid .frame .buttons -sticky ns -pady {0 10} 
     . configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
    bind . <Motion> {wm title . "Probablity N-sided Double Dice Slot Calculator Example "}

The testcase 4a was 3 dice rolling all ones. The sample size was 6**3 or 216.

 set zz [ expr { 6**3 } ]

The probability of getting all ones from 3 dice was 1/(6**3) or 0.0046296.

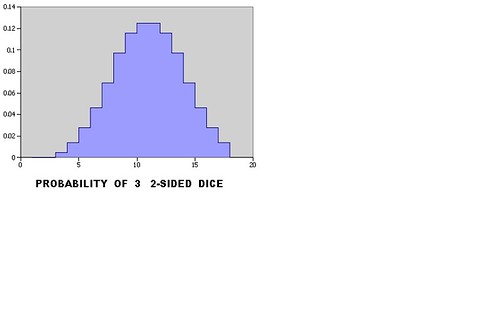
 set xx [ expr { 1./(6**3) } ]

Printout for all throws of 3 dice

printout for all throws of 3 dice. set tcl_precision 17 was not used here, but I can't tell much difference.

 1 0.0 
 2 0.0 
 3 0.004629629629629629 
 4 0.013888888888888888 
 5 0.027777777777777776 
 6 0.046296296296296294 
 7 0.06944444444444445 
 8 0.09722222222222222 
 9 0.11574074074074074 
 10 0.125 
 11 0.125 
 12 0.11574074074074074 
 13 0.09722222222222222 
 14 0.06944444444444445 
 15 0.046296296296296294 
 16 0.027777777777777776 
 17 0.013888888888888888 
 18 0.004629629629629629 
 #end

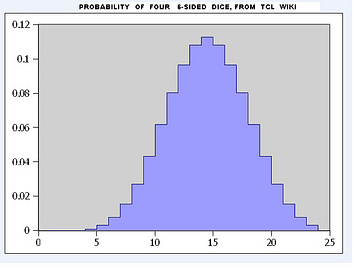
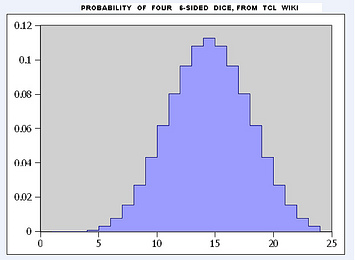
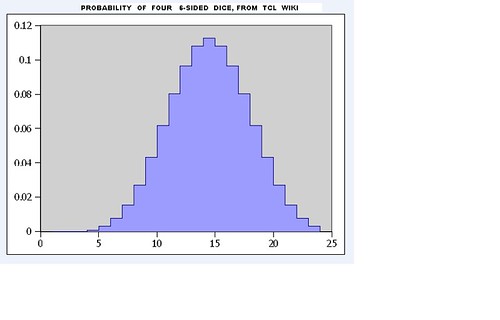
Printout for all throws of 4 dice

all throws of 4 dice set tcl_precision 17 (on)

 1 0.0 
 2 0.0 
 3 0.0 
 4 0.0007716049382716049 
 5 0.0030864197530864196 
 6 0.007716049382716049 
 7 0.015432098765432098 
 8 0.027006172839506171 
 9 0.043209876543209874 
 10 0.061728395061728392 
 11 0.080246913580246909 
 12 0.096450617283950615 
 13 0.10802469135802469 
 14 0.11265432098765432 
 15 0.10802469135802469 
 16 0.096450617283950615 
 17 0.080246913580246909 
 18 0.061728395061728392 
 19 0.043209876543209874 
 20 0.027006172839506171 
 21 0.015432098765432098 
 22 0.007716049382716049 
 23 0.0030864197530864196 
 24 0.0007716049382716049 
 end

The testcase 5a was 5 dice rolling all sixes. The sample size was 6**5 or 7776.