Biruni Estimate of Earth Diameter Slot Calculator eample
Biruni Estimate of Earth Radius Slot Calculator Example
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 12Dec2018
Introduction
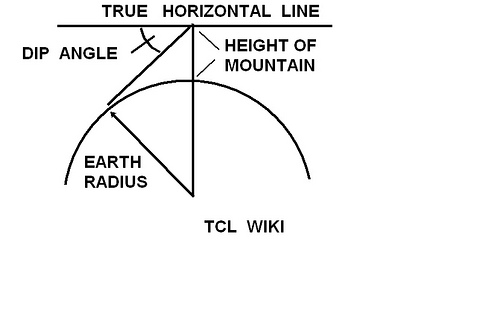
gold Here is an eTCL script on to estimate the radius or diameter of the earth using Al Biruni figures and method from the text Masudi Canon. An equation for the dip angle and height of mountain was used in computing the earth's radius. The equation is striking in that the equation involved a single location versus two locations. Spelled Al Biruni , Al Beruni, Al Bayrooni (born 5 September 973 CE)
testcase 1 from Biruni's calculation as reported
- height was 652+1/20 cubits
- radius was 12851359cubits
- circumference was 80780039 cubits
- arabic cubit ~ 4,933 mm
- circumference ~ 25000+2/7 english miles
- dip reportedly 34 minutes
- testcase was height 479 meters,
- 479 meters is modern survey of Nandian Mountain.
- Persian cubit of about 500.1 mm,
- dip angle was 30 or 34 minutes,
- 30/60 degree or 34/60 degrees.
- (652.05 cubits * cos (.56666) / (1 - cos(.56666) = ?
- Very sensitive equation, cosine would have to be known to 5th position.
- Biruni's answer was in Persian cubits
| quantity | number | units |
|---|---|---|
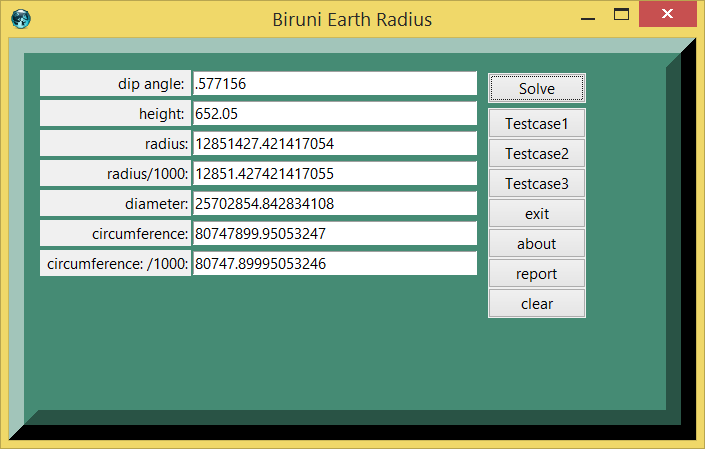
| dip angle: | .577156 | degrees |
| height: | 652 | cubits |
| radius: | 12851427.421417054 | cubits |
| radius/1000 : | 12851.427421417055 | kilocubits |
| diameter: | 25702854.842834108 | cubits |
| circumference: | 40373949.97526623 | cubits |
| circumference/1000: | 80747.89995053246 | kilocubits |
- reverse on Biruni's angle constant
- 652.05/(1-x)=r
- 652.05*x=r(1-x)
- x= r(652.05+r)= 0.99949265 radians
- or 0.577156 degrees.
- Loading 0.577156 degrees and 652.05 cubits, calculator is getting 12851427 cubits, close to Biruni's answer.
- For meters, the Nandian survey height as 479 meters? ... Anyway.
- Loading 652.05 cubits *.5 or 326.025 meters and 0.577156 degrees is returning 6425.714 kilometers
- Modern estimate of earth radius at equator is 6356.75 km.
- Biruni overage is about 1.08 percent.
testcase 2 output from meters entry
| quantity | number | units |
|---|---|---|
| dip angle: | .577156 | degrees |
| height: | 326.025 | meters |
| radius: | 6425713.710708527 | meters |
| radius/1000 : | 6425.713710708527 | kilometers |
| diameter: | 12851427.421417054 | meters |
| circumference: | 40373949.97526623 | meters |
| circumference/1000: | 40373.94997526623 | kilometers |
While the testcase above is in cubits, the units cancel out in the equation. So the units could entered as kilometers, nautical miles, English miles, or Chinese miles. This is an advantage since the units in the ancient Persian, Indian, and Chinese texts are open to question.
Trying to find some earlier estimates of earth's circumference from other cultures. Most of the early constants were given underived without sources. Scanty sources and circular reasoning { no good text reference} speculates that the Sumerians might have used 3600 beru as circumference, with the earth circumference as 3600*10.8 km. Given ~, the earth radius would be 573 beru 9_33,base 60) and diameter would be 1146 beru (19_6,base 60). Still trying to find out if "miles" on clay tablet BM 92687 are beru or else.
Posidonius of Rhodes (ca. 135 BCE - 51 BCE) made two estimates of the earth diameter. The first estimate was 24000 miles or 38600 kilometers in modern terms. The second estimate was 18000 miles or 28900 kilometers. For comparison, the first estimate was 38880 / 38600; 1.00725389, within 0.7 percent of the Sumerian estimate.The second estimate was 38880 / 28900 = 1.34532872, within 34.5 percent of the Sumerian estimate. Within reasonable rounding error, the first estimate of Posidonius was the same as the Sumerian estimate.
On Sumerian clay tablet, there are 655200 "beru ina sama" summed up, Akkadian for "beru in sky." This factors to 364*60*30. There are 86400 seconds in a day. There are 655200 beru in sky over 360 conventional degrees or 1820 per degree. The apparent disk of sun or moon was supposed to be 1000 beru (~to 0.5 degree). In conventional astronomy, a degree contains 60*60 or 3600 arcseconds. So a beru in sky may something like a double second (meaning double arcsecond). In modern constants, a double arcsecond would be equivalent to 1800/111.3km or 16.17 double arcseconds per km ( from one latitude degree equals 111.3 km). A sky triangle of one degree and an opposite side of 1800 would have a side of 1800/tan(1) or 103137.638. A second and almost equal side would be 1800/sin(1) or 103121.93. considerations for circle, 360*60*60=1296000 364*60*60=1310400 , say 1310400/2=655200.
Found some references to early Sumerian translations that there were 3600*12 sky cubits in 360 degrees or 12 beru (double hours). There would be 3600*12/360 or 43200/360 or 120 sky cubits in a degree. Another early reference held that a sky cubit was equivalent to 150 nindans (0.5 meter). Hence the constant would be 120*150*6 or 108000 meters or 108 kilometers in a degree. Hence an earth circumference of 108*360 or 38880 kilometers would be implied. Ref. Thureau Dagin, RA28
Arithmetic Classic of the Gnomon and the Circular Paths of Heaven reported triplet as follows.
- 60000 li, 24948 km, 15502.2 miles
- 80000 li, 33264 km, reputed altitude of sun,
- 100000 li, 41580 km, reputed distance from measuring stick to sun
Chinese li was 0.4158 km (0.25837 miles). 2* babylonian 12709 =25418
Chen Zi of first century reported indirect numbers leading to earth diameter of 911489 li or 378990km. Chen Zi placed tropic of cancer +23.5 latitude at 16000 li south of his location, using modern terms. Chen Zi placed tropic of capricorn -23.5 latitude at 135000 li south of his location, using modern terms. difference of tropic latitude is +23.5-(-23.5) or 47 degrees. Ratio of 47 degree tropic difference to 360 circumference is 47/360. 47/360=(135000-16000)/x x =(135000-16000)/(47/360) x= 119000/(47/360) x = 911490 li or 911490 li*.415 km/li or 378268 km. It seems his li in the text has a factor of ten involved. ChenZi was probably using rod numerals and it is very easy to develop order of magnitude uncertaincy in subsequent copies, without the use of place value and zero. The "li" in the text is about 0.043958 km or 43.958 meters. The number 119000 is mentioned several times in the text, and appears to apply to the distance between the tropics, although subject to interpretation. Can only suggest Chen Zi's number for the earth circumference was 37900. km and implied constant was 105.27 km per degree, in modern terms.
| place/person | date | circumference in modern units |
|---|---|---|
| Eratosthenes | third century BCE | 46250 km |
| Ptolemy | c140CE | 28800 km |
The giant of Chinese legend Pan Gu (or panku, ancient basin) held the earth and sky apart at 90000 li (45000 km). The Egyptians held that the N/S length of Egypt was 1/50 of the globe circumference. The Romans use 75 roman miles as eq to one degree of latitude. The Mogul era "Ain" states the earth's circumference was 8000 farsakh (1600CE).8000 farsakh *5.76 km /farsakh =46080km In some texts of Aryabhatiya, the diameter of the earth is mentioned as 3300 yojanams. Brahmagupta ( 7th c) wrote that the circumference of the earth was 36,000 km, in modern units. one arabic isba =1.6 degrees= one chinese zhi=1.6 deg * 111.3 km/deg=178.08 km one chinese jiao (Ming, period at least) = 1.6/4 or 0 .4 degrees*111.3 km/deg = 44.5 km The length between the eye and the qianxingban board was 55.4 centimeters, Ming period. Pulls star board, # # # , qianxingban 1 deg width of a little finger at arm's length,111.3 km 1.6 deg width of middle finger at arm's length,178.08 km 10 deg the width of a closed fist at arm's length,1113 km, 20 deg width of a handspan at arm's length,2226 km, 713-741 ce, Nangong Yue and Tang Yixing, tang dynasty one deg. latitude equals 351 li and 80 bu (351.26 tang_li???) (129.2km) 351.26 tang_li* 360deg =46512km.
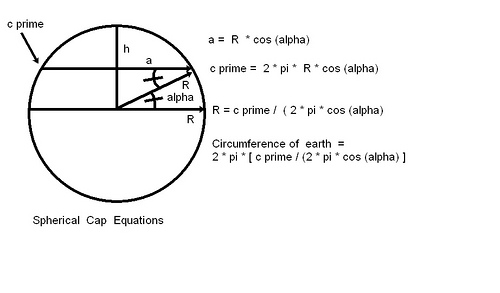
Sumerian trials. The Sumerian astronomers divided the sky into three zones known as the way of Enhil, the way of Anu, and the way of Ea. The way of Enhil was above 17 degrees and totaled 538 units. The way of Anu was between minus 17 degrees and plus 17 degrees and totaled 1080 units. The way of Ea was beyond minus 17 degrees and totaled 2160 units. While these zones appear to suggest a celestial sphere and possibly a spherical earth, the terms celestial equator, Tropic of Cancer, Tropic of Capricorn and celestial south pole were not used by the Sumerians. The Tropics (now at +-23.5 degrees, respectively) have changed over the millennia, so the estimates of +-17 degrees for the Enhil etc bounds may not be reliable. The ratios of the way of Enhl,Anu,& Ea would be 1080/538 (2.007) , 2160/1080 (2.) , and 2160/538 (4.01). In modern terms, the Way of Enhil included stars and constellations in the middle northern latitudes and above the Greek Zodiac.The way of Anu corresponded to the celestial elliptic and included stars and constellations which correspond to the Greek Zodiac. The way of Ea included stars and constellations south of the celestial equator. The Way of Enhil included stars and constellations in the middle northern latitudes and above the Greek Zodiac. However by trigonometry of a spherical cap of height h, the circumference of a slice which is h-R above the center of the sphere is cprime= 2.*pi* a, where a is the radius of the slice. Since a = R cos(alpha), where R is the radius of the sphere and alpha is the angle between the sphere radius and the slice. We find that c prime = 2*pi*R*cos(alpha) and hence R = c prime *(scaling factors) /(2*pi*cos(alpha)).
| person/place | circumference in modern units | percent rel to 40080 km | period or date |
|---|---|---|---|
| Sumeria | 38880 km? 3600 beru? | 3.08 percent short | Sargonic empire,2270 to 2215 BC |
| Posidonius of Rhodes | 38600km | 3.8 percent short | (ca. 135 BCE - 51 BCE) |
| Posidonius of Rhodes | 28900km | 38.6 percent short | (ca. 135 BCE - 51 BCE) |
| Eratosthenes, Cyrene | 46250 km | 15.6 percent high | 3ird century |
| Ptolemy, Egypt | 28800km | 15.6 percent low | circa 140 CE |
| Aristotle, Syracuse | 48000 km | 19.9 percent high | 384 BC – 322 BC |
| Chen Zi, China | 37826.8 km | 5.7 percent short | 1st century |
| Biruni, Persia | 39834.7 km | 0.4 percent short | 937 CE |
| Brahmagupta, India | 36,000 km | 11.1 per cent short | 598–668 CE |
| Roman (2nd c) | 39933 km | 0.187 percent short* | 2nd century |
| Tang dynasty, China | 46512 km | 16 percent high | 700 CE |
| caliph al-Ma'mun, Iraq | 37380 km | 7 percent short | 900 CE |
| Arabia/India sailors | 35840 | 11 percent short ** | 1550 CE |
| Newton, UK | 40123 | 0.1 percent high | 1643 – 1727 |
* meaning 75 roman miles/deg * 360. deg. *1.479 scale km/r. mile
** sailor's marks , 224 isba * 8 zams per isba * 20 km per zams
arabic zam = sanscrit zama = Muldive Dhevehi dama ref. sumerian dana???
lateen day's sail will raise pole star one isba.Screenshots Section
figure 1.
figure 2.
figure 3.
References:
- http://www.highbeam.com/doc/1G2-2830900460.html
- http://en.wikipedia.org/wiki/Biruni
- The history of cartography, Volume 2 By John Brian Harley, David Woodward
appendix TCL programs and scripts
Pretty Print version
# test indent from ased editor
# Biruni Estimate of Earth Diameter
# written on Windowws XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI , 8aug2010
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {dip angle: } {height: } {radius:} {radius/1000:} {diameter:} {circumference:} { circumference: /1000:}}
foreach i {1 2 3 4 5 6 7} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1
}
proc about {} {
set msg "Calculator for Biruni Earth Radius.
from TCL WIKI,
written on eTCL "
tk_messageBox -title "About" -message $msg
}
proc pi {} {expr acos(-1)}
proc strat5 { xx1 } {
global side1 side2 side3
global side4 side5 side6 side7
set ss side1
set tt $side2
set xxx [ expr { $side1*[pi]/180. } ]
set side3 [ expr { 1.*$side2*cos($xxx)/(1.-1.*cos($xxx))} ]
set side3 [ expr { 1.*$side2*cos($xxx)/(1.-1.*cos($xxx))} ]
set side4 [ expr { (1.*$side3)*.001 } ]
set side5 [ expr { (1.*$side3)*2. } ]
set side6 [ expr { (1.*$side3)*2.*[pi] } ]
set side7 [ expr { (1.*$side3)*2.*[pi]*.001 } ]
return $side3
}
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5 side6 side7
set answer2 5
set answer2 [ strat5 $side3 ]
set side3 $answer2
}
proc fillup {aa bb cc dd ee ff gg} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff "
.frame.entry7 insert 0 "$gg "
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7} {
.frame.entry$i delete 0 end
}
}
proc reportx {} {
console show;
puts " "
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup .577156 652.05 12.85E6 12.85E3 2.57E6 8E6 8E4}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup .577156 479 9.44E6 9.44E3 18.9E6 5.9E6 5.9E4}
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup .56666 652.05 13.33E6 1.33E4 26.6E6 8.3E6 8.3E4}
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command about
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Biruni Earth Radius"
gold This page is copyrighted under the TCL/TK license terms, this license .
Comments Section
Comments Section
Please place any comments here, Thanks.
What is your purpose in binding the motion event on your main window to execute the wm title command. I.e., this line:
bind . <Motion> {wm title . "Biruni Earth Diameter"}The result of that binding is that every time you move the mouse, the "wm title" subcommand is called repeatedly. To set the window title, you just need to call "wm title . title" once, not on every event update upon mouse pointer motion.
gold changed to bare "wm title . title"
Please place any comments here, Thanks.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |