Bwise block of the month
Well, not really, but that sounds funny, of the year, more likely!
Anyhow, anyone wanting to share a bwise block: by all means!
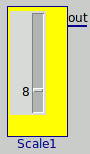
Didn't know which page, of the several dozen bwise pages, to put this on. A slider input for bwise.
proc newscale { {width {60}} {height {130}} {tags {}} {name {}} {x {0}} {y {0}} {in {}} {out {out}} } {
if {$name == {}} {
uplevel #0 {if {[info exists entrycount] == "0"} {set entrycount 0} ;}
global entrycount
incr entrycount
set name Scale$entrycount
}
set t [blockfunc $name]
global mc $t;
newblock $name $x $y $width $height $in $out $tags
blockclear $name
set lc [string tolower $name]
set cmd " uplevel #0 run $name"
scale $mc.$lc -from 0 -to 10 -length 100 -sliderlength 5 -width 10 -tickinterval 0 -variable $name.out -command $cmd
$mc create window [expr $x+3] [expr $y+5] -window $mc.$lc -tags "{$name}" -anchor nw
if {$in == "in"} {
set $name.bfunc "set $name.out \${$name.in}"
}
return $name
}TV Looks nice.
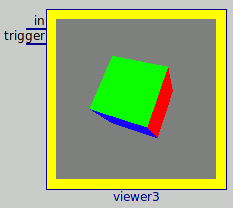
I'm working on a bwise 3D graphics viewer block :
Using these lines:
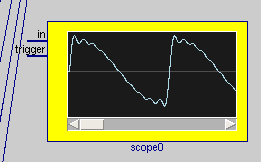
time {set r [domaxima float(makelist(subst(y/44100,x,subst((1/2),v,${mult11.out})),y,0,170))]}
eval ${scope0.bfunc_init} ;foreach i [split [string range $r 1 end-1] ,] { set scope0.in [expr 300*$i] ; eval ${scope0.bfunc} }(see Creating wave formulas with BWise for the context and procs required) this is a mathematically correct waveform, without use of expr or libc or even doubles until the very last rounding step in the computations, so suitable for numerically 'dificult' waves:
This one's nice to remember:
from A musical keyboard for BWise and Midi connections.