Continued Fraction
Keith Vetter 2016-06-15 : This is a tool I wrote a few years ago when I was playing around solving problems from Project Euler.
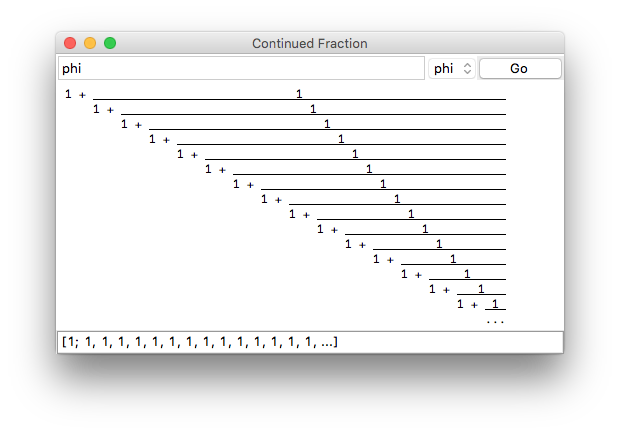
This tool will display an expression's continued fraction both as a list of coefficients and as a fraction. It's limited by the precision of Tcl's double but does some tricks to ameliorate the problem. It also understands the symbols "pi", "e" and "phi" plus all of Tcl's normal math functions.
Every rational number has a finite continued fraction. Periodic Infinite continued fractions are precisely the quadratic irrationals. For example, [1;1,1,1,...] is the golden ratio, and [1;2,2,2,...] is the square root of 2. Pi, on the other hand, has an apparently random continued fraction of [3;7,15,1,292,1,1,...].
##+##########################################################################
#
# Continued Fractions -- Displays the continued fraction for a number,
# either on the console or, if running with Tk, in a window.
# Note: limited by the precision of a double
#
# by Keith Vetter 2013-08-21
# More info: https://en.wikipedia.org/wiki/Continued_fraction
# See also: https://www.wolframalpha.com/input/?i=continued+fraction+sqrt(2)
#
set S(depth) 15
set S(examples) {
"phi" "pi" "e" "5/7" "sqrt(2)" "sqrt(3)" "tan(1/2.)" "tan(1/3.)"
}
set S(expression) [lindex $S(examples) 0]
proc DoDisplay {} {
global S
if {! [info exists ::tk_version]} return
wm title . "Continued Fraction"
::tk::entry .expression -textvariable S(expression)
tk_optionMenu .examples S(expression,example) {*}$S(examples)
for {set i 0} {$i < [llength $S(examples)]} { incr i } {
[winfo child .examples] entryconfig $i -command {Go $::S(expression,example)}
}
::ttk::button .go -text "Go" -command {Go $::S(expression)}
::tk::label .linear -textvariable S(linear) -bg white -bd 2 -relief ridge -anchor w -padx 2m
text .t -height [expr {$S(depth)+1}] -width 70 -wrap none -padx 2m -state disabled
.t tag config under -underline 1
grid .expression .examples .go -sticky ew
grid .t - - -sticky news
grid .linear - - -sticky ew
grid rowconfigure . 1 -weight 1
grid columnconfigure . 0 -weight 1
bind .expression <Key-Return> {.go invoke}
}
proc Go {expression} {
set ::S(expression) $expression
lassign [QuickParseExpression $expression] numExpression denExpression
lassign [MakeRational [SafeMath $numExpression] [SafeMath $denExpression]] num den
set cf [ComputeCF $num $den]
set ::S(linear) [PrettyCF $cf]
ShowCF $cf
}
proc QuickParseExpression {expression} {
# Continued fractions work best with integers, so if we can determine that the expression
# is of the form "a / b" then we can make the denominator "b" and get better accuracy.
# Also, for convenience, convert "pi", "e", and "phi" into their mathematical equivalence.
foreach {word value} {"pi" "acos(-1)" "e" "exp(1)" "phi" "((1 + sqrt(5))/2)"} {
set expression [regsub -all "\\m$word\\M" $expression $value]
}
while {[regexp {^ *\( *(.*) *\) *$} $expression . expression]} { continue }
set lastDivide -1
set parenCount 0
for {set i 0} {$i < [string length $expression]} {incr i} {
set ch [string index $expression $i]
if {$ch eq "("} { incr parenCount ; continue }
if {$ch eq ")"} { incr parenCount -1 ; continue }
if {$ch eq "/" && $parenCount == 0} { set lastDivide $i ; continue }
}
if {$lastDivide == -1} {
return [list $expression 1]
}
return [list [string range $expression 0 $lastDivide-1] [string range $expression $lastDivide+1 end]]
}
proc ComputeCF {n m {maxDepth 0}} {
set result {}
if {$maxDepth <= 0} { set maxDepth $::S(depth) }
for {set depth 0} {$depth < $maxDepth} {incr depth} {
set integer [expr {$n/$m}]
lappend result $integer
set n [expr {$n - $integer * $m}]
if {$n == 0} break
lassign [list $n $m] m n
}
if {$n > 0} {
lappend result "..."
}
return $result
}
proc ShowCF {cf} {
global THIS ALL
if {! [info exists ::tk_version]} {
puts "$::S(expression) => [PrettyCF $cf]"
puts [join [PrettyPrint $cf] \n]
return
}
GetSizesForDisplaying $cf
.t config -state normal
.t delete 0.0 end
set prefix ""
for {set i 0} {$i < [llength $cf]-1} {incr i} {
set j [expr {$i+1}]
set value [lindex $cf $i]
set pre [expr {$ALL($j)/2}]
set post [expr {($ALL($j)-1)/2}]
set one [string repeat " " $pre]1[string repeat " " $post]
set line "$prefix$value + "
.t insert end $line normal $one under \n
append prefix [string repeat " " $THIS($i)]
}
.t insert end "$prefix[lindex $cf end]"
.t config -state disabled
}
proc PrettyCF {cf} {
set rest [lassign $cf first]
return "\[$first; [join $rest {, }]\]"
}
proc PrettyPrint {cf} {
global THIS ALL
GetSizesForDisplaying $cf
set prefix ""
set lines {}
for {set i 0} {$i < [llength $cf]-1} {incr i} {
set j [expr {$i+1}]
set value [lindex $cf $i]
set blanks [expr {$THIS($i) + $ALL($j)/2}]
set line0 "$prefix[string repeat { } $blanks]1"
set line1 "$prefix$value + [string repeat {-} $ALL($j)]"
lappend lines $line0 $line1
append prefix [string repeat " " $THIS($i)]
}
set line "$prefix[lindex $cf end]"
lappend lines $line
return $lines
}
proc GetSizesForDisplaying {cf} {
global THIS ALL
unset -nocomplain THIS
unset -nocomplain ALL
set len [expr {[llength $cf] - 1}]
for {set i $len; set last 0} {$i >= 0} {incr i -1} {
set value [lindex $cf $i]
set THIS($i) [set ALL($i) [string length $value]]
if {$last > 0} {
incr THIS($i) 3
incr ALL($i) 3
incr ALL($i) $last
}
set last $ALL($i)
}
}
proc MakeRational {num den} {
if {[string is entier $num] && [string is entier $den]} {
return [list $num $den]
}
set num_frac [string length [lindex [split $num "."] 1]]
set den_frac [string length [lindex [split $den "."] 1]]
set size [expr {max($num_frac,$den_frac)}]
set scale "1[string repeat 0 $size]"
set num [expr {int($num * $scale)}]
set den [expr {int($den * $scale)}]
set gcd [gcd $num $den]
set num [expr {$num / $gcd}]
set den [expr {$den / $gcd}]
return [list $num $den]
}
proc gcd {p q} {
while {$q != 0} {set q [expr {$p % [set p $q]}]}
return [expr {abs($p)}]
}
proc ReverseCF {cf} {
lassign {1 0} num den
foreach term [lreverse $cf] {
lassign [list [expr {$term * $num + $den}] $num] num den
}
return [list $num / $den]
}
proc SafeMath {expression} {
interp create -safe newInterp
try {
set value [newInterp eval expr \{ $expression \}]
} on error {result option} {
error "bad expression: '$expression'"
} finally {
interp delete newInterp
}
return $value
}
################################################################
DoDisplay
if {$argv eq {}} {
Go [set S(expression,example) [lindex $S(examples) [expr {int(rand()*[llength $S(examples)])}]]]
} else {
Go [lindex $argv 0]
}
returnAK - 2016-06-16 03:46:57
Related: Kevin Kenny's paper about Exact Real Arithmetic in Tcl (pdf) . He uses Moebius-Transforms to represent real numbers. Section 3.3 mentions continued fractions as an earlier attempt. More proceedings at https://www.tcl-lang.org/community/tcl2015/proceedings.html
AMG: Related: https://youtu.be/0z1fIsUNhO4