Fern Fractal
Keith Vetter 2003-12-01 : This image of a Black Spleenwort fern is often called the Barnsley's Fern after Michael Barnsley. It is one of the best known of the Iterated Function System (IFS) fractals. Actually, while everyone calls it a fractal technically it's not--it's not self-similar but self-affine.
An IFS takes a point and performs an affine transformation--translation, rotation and contraction--on it, then repeats. For the fern, there are four affine transformation that are used with certain probabilities.
See also IFS for a page with more general IFS fractals.
DKF: Oooh! I like it!
##+##########################################################################
#
# Fern.tcl - description
# by Keith Vetter -- November 30, 2003
#
# This image of a Black Spleenwort fern is often called the Barnsley's
# Fern after Michael Barnsley. It is one of the best known of the
# Iterated Function System (IFS) fractals (technically it's not a
# fractal but everyone calls it one). An IFS takes a point and
# performs an affine transformation--translation, rotation and
# contraction--on it, then repeats. For the fern, there are four
# affine transformation that are used with certain probabilities.
# Define our affine transformations
# (x,y) <== (rx(cos(A)) - sy(sin(B)) + h, rx(sin(A)) + sy(cos(B)) + k)
# (x,y) <== (ax + by + h, cx + dy + k)
array set TRANS {
- {P a b h c d k}
0 {0.02 0.0 0.0 0.5 0.0 0.27 0}
1 {0.15 -.139 0.263 0.57 0.246 0.224 -.036}
2 {0.13 0.17 -.215 0.408 0.222 0.176 0.0893}
3 {0.70 0.781 0.034 0.1075 -.032 0.739 0.27}
}
array set S {title "Fern Fractal" W 500 H 500 color green}
proc OnePixel {} {
global S xx yy TRANS
# Pick which transformation to use
set rand [expr {rand()}]
for {set i 0} {$i < 3} {incr i} {
set p [lindex $TRANS($i) 0]
if {$rand < $p} break
set rand [expr {$rand - $p}]
}
# (x,y) <== (ax + by + h, cx + dy + k)
foreach {p a b h c d k} $TRANS($i) break
foreach xx [expr {$a*$xx + $b*$yy + $h}] \
yy [expr {$c*$xx + $d*$yy + $k}] break
set sx [expr {$S(W) * $xx}] ;# Map to screen coordinates
set sy [expr {$S(H) - ($S(H) * $yy)}] ;# Make fern grow upwards
.c create rect $sx $sy $sx $sy -fill $S(color) -outline {}
return
}
proc Run {} {
foreach id [after info] {after cancel $id} ;# Be safe
if {$::S(go)} {
OnePixel
after 1 Run
}
}
proc tracer {var1 var2 op} {
if {$::S(go)} {
.start config -state disabled
.stop config -state normal
Run
} else {
.start config -state normal
.stop config -state disabled
}
}
proc Resize {W h w} {
foreach ::S(H) $h ::S(W) $w break
Reset
}
proc Reset {} {
.c delete all
set ::xx [expr {rand()}]
set ::yy [expr {rand()}]
}
proc DoDisplay {} {
global S
wm title . $S(title)
pack [frame .ctrl -relief ridge -bd 2 -padx 5 -pady 5] \
-side right -fill both -ipady 5
pack [frame .top -relief ridge -bd 2] -side top -fill x
pack [frame .screen -bd 2 -relief raised] -side top -fill both -expand 1
canvas .c -relief raised -bd 2 -height $S(H) -width $S(W) -bg black
pack .c -side top -in .screen -fill both -expand 1
set colors {red orange yellow green blue cyan purple violet white black}
foreach color $colors {
radiobutton .top.b$color -width 1 -padx 0 -pady 0 -bg $color \
-variable S(color) -value $color
bind .top.b$color <3> [list .c config -bg $color]
}
eval pack [winfo children .top] -side left -fill y
DoCtrlFrame
bind all <Key-F2> {console show}
bind .c <Configure> {Resize %W %h %w}
trace variable S(go) w tracer
update
}
proc DoCtrlFrame {} {
option add *Button.borderWidth 4
button .start -text "Start" -command {set S(go) 1}
.start configure -font "[font actual [.start cget -font]] -weight bold"
option add *Button.font [.start cget -font]
button .stop -text "Stop" -command {set S(go) 0}
button .reset -text "Reset" -command Reset
button .about -text About -command [list tk_messageBox -title $::S(title) \
-message "$::S(title)\nby Keith Vetter, November 2003"]
grid .start -in .ctrl -row 1 -sticky ew
grid .stop -in .ctrl -row 2 -sticky ew
grid .reset -in .ctrl -row 3 -sticky ew -pady 10
grid rowconfigure .ctrl 50 -weight 1
grid .about -in .ctrl -row 100 -sticky ew
}
DoDisplay
set S(go) 1uniquename 2013aug18
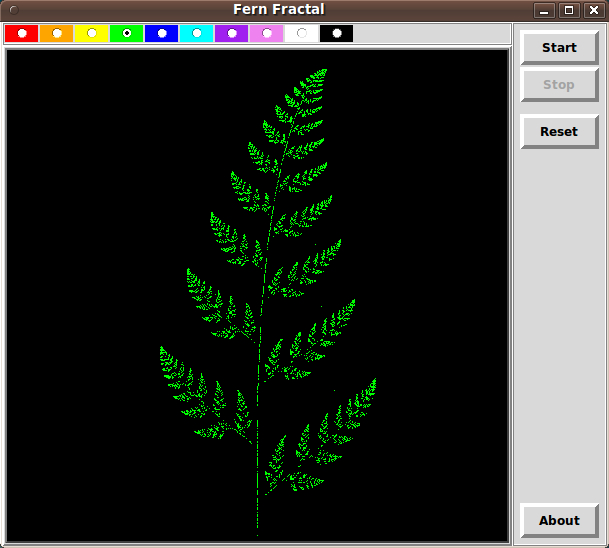
For readers who do not have the time/facilities/whatever to setup the code and execute it, here is an image to show what the code above does.
After the GUI popped up with a black canvas, the fern started drawing in. I clicked the 'Stop' button after several seconds (on a little netbook computer) and captured the image above.
And here is an image that was generated by the 'Fractal Picture' code of AM below. This image popped up complete within a second after I started the AM script --- again on a little netbook computer (Intel Atom N450 chip).
AM (13 august 2009) Here is another example of this technique - just for fun. As at each step a complete picture is drawn, the number of pictures is much smaller than the number of points in the Fern Fractal. I experimented with this to see if it would make a good design for a "flyer".
# fractal_picture.tcl --
# Experiment with a fractal picture
#
# drawPicture --
# Draw the new scaled and dislocated picture
#
# Arguments:
# xc X-coordinate to use (centre)
# yc Y-coordinate to use (centre)
# scale Scale of the picture
#
proc drawPicture {xc yc scale} {
set coords {}
foreach {xp yp} {-50 -50 -50 50 50 50 50 -50} {
lappend coords [expr {$xc + $scale * $xp}] \
[expr {$yc + $scale * $yp}]
}
.cnv lower [.cnv create polygon $coords -fill green -outline black]
}
# nextGeneration --
# Produce the next generation of pictures
#
# Arguments:
# previous Triples describing the previous generation
#
# Returns:
# Flattened list of triples for the new generation
#
proc nextGeneration {previous} {
set next {}
set factor 0.5
foreach {xc yc scale} $previous {
set scale [expr {$factor * $scale}]
foreach {xa ya} {0 0 500 0 500 500 0 500} {
set xn [expr {$xa + $factor * ($xc-$xa)}]
set yn [expr {$ya + $factor * ($yc-$ya)}]
drawPicture $xn $yn $scale
lappend next $xn $yn $scale
}
}
return $next
}
# main --
# Draw the thing
#
pack [canvas .cnv -width 500 -height 500]
set pictureParameters {250 250 1.0}
drawPicture 250 250 1.0
foreach generation {0 1 2 3 4 5} {
set pictureParameters [nextGeneration $pictureParameters]
}AM (2 january 2022) I came across two more examples of an iterated function system (a book by Bailey et al. , and implemented them in the script below. Nothing fancy, mind you, but you can watch the picture grow ...
# ifs.tcl --
# Some more IFS examples:
# - Sierpinski triangle
# - Twin dragon
#
global offset
global scale
global count
set offset 10
# draw --
# Draw a point
#
proc draw {c x y} {
global xmin
global ymin
global scale
global count
global offset
set x [expr {$offset + ($x - $xmin) * $scale}]
set y [expr {$offset + ($y - $ymin) * $scale}]
$c create rectangle $x $y $x $y
incr count
if { $count % 100 == 0 } {
set count 0
update
}
}
# sierpinski --
# Draw a Sierpinski triangle
#
# Arguments:
# c Canvas to draw in
# n Number of iterations
#
proc sierpinski {c n} {
global xmin
global ymin
global scale
global offset
set x1 1.0; set y1 0.0
set x2 -1.0; set y2 0.0
set x3 0.0; set y3 [expr {sqrt(3.0)}]
set x [list $x1 $x2 $x3]
set y [list $y1 $y2 $y3]
set xo 0.0
set yo 0.0
set width [$c cget -width]
set xmin -1.0
set ymin 0.0
set scale [expr {$width / 2.1}]
for {set i 0} {$i < $n} {incr i} {
set r [expr {int(3.0 * rand())}]
set xn [expr {0.5 * ($xo + [lindex $x $r])}]
set yn [expr {0.5 * ($yo + [lindex $y $r])}]
draw $c $xn $yn
set xo $xn
set yo $yn
}
}
# twindragon --
# Draw a "Twin dragon"
#
# Arguments:
# c Canvas to draw in
# n Number of iterations
#
proc twindragon {c n} {
global xmin
global ymin
global scale
global offset
set x1 0.0; set y1 0.0
set x2 1.0; set y2 0.0
set x [list $x1 $x2]
set y [list $y1 $y2]
set xo 0.0
set yo 0.0
set width [$c cget -width]
set xmin -0.75
set ymin -0.25
set scale [expr {$width / 2.1}]
for {set i 0} {$i < $n} {incr i} {
set r [expr {int(2.0 * rand())}]
set xr [lindex $x $r]
set yr [lindex $y $r]
set xx [expr {$xo + $xr}]
set yy [expr {$yo + $yr}]
set xn [expr {0.5 * ($xx - $yy)}]
set yn [expr {0.5 * ($xx + $yy)}]
draw $c $xn $yn
set xo $xn
set yo $yn
}
}
# Set up the canvases and draw
set count 0
pack [canvas .c1 -width 500 -height 500] [canvas .c2 -width 500 -height 500] -side left
sierpinski .c1 10000
twindragon .c2 10000The result on my system is this: