Imperiali
Calculate number of seats per party using the 'Imperiali' system as used in Flanders (Belgium) for local elections.
Each party gets a vote count. This vote count is the number of votes for the party. This count includes:
- Votes for the party only
- Votes for the party and one or more individuals of the same party
- Votes for one or more individuals of the same party
Each of the above counts as '1' in the vote count.
To calculate the seats, all vote counts are divide by 2, 3, 4, 5, 6, ... These division results are sorted high to low and seats are allocated according to this sorted list. When allocating the last seat and the division results are equal for two or more parties, the party with the largest vote count gets the seat.
When the vote count is also equal, the candidate with the most individual votes gets the seat. If they have the same number of individual votes, the oldest candidate gets the seat. These last two rules are not implemented in this script.
When not sure which party gets the seat, the seats still to be decided are colored orange. Allocated seats are colored green.
# List of parties
set partl {a b g h k}
# Maximum number of candiates per party, also number of seats to be chosen
set kandmax 17
# Number of candidates per party
set kandl(a) 17
set kandl(b) 17
set kandl(g) 17
set kandl(h) 1
set kandl(k) 17
###############################################################################
# Make no changes below this line
###############################################################################
set f [frame .f]
pack $f -fill both -expand true
set col 0
set row 0
# Naan van partijen
incr row
set l1 [label $f.lstemc -text "Vote count"]
grid $l1 -column $col -row $row
incr row
for { set i 0 } { $i < $kandmax } { incr i } {
set l [label $f.lkand$i -text $i]
grid $l -column $col -row $row
incr row
}
set row 0
incr col
foreach part $partl {
set l0 [label $f.l$part -text $part -bd 1 -relief raised]
grid $l0 -column $col -row $row -sticky ewns
incr row
set stemcijfer($part) 0
set e1 [entry $f.esc$part -textvariable stemcijfer($part) -width 10 -justify right]
grid $e1 -column $col -row $row -sticky ewns
incr row
for { set i 0 } { $i < $kandl($part) && $i < $kandmax } { incr i } {
set quotienteff($part,$i) 0
set quotient($part,$i) 0
set l [label $f.quot$part$i -textvariable quotient($part,$i) -width 14 -anchor e \
-justify right -bd 1 -relief raised]
grid $l -column $col -row $row -sticky ewns
incr row
}
set row 0
incr col 2
}
set b [button .b -text Calculate -command bereken]
pack $b
proc sort_qe_sc { a b } {
foreach {aqe asc apart ai} $a { break }
foreach {bqe bsc bpart bi} $b { break }
if { ($aqe < $bqe) || ($aqe == $bqe && $asc < $bsc) } {
return -1
} elseif { $aqe == $bqe && $asc == $bsc } {
return 0
} else {
return 1
}
}
proc bereken { } {
global partl kandmax kandl stemcijfer lijst voorkeur quotient f
set ql {}
foreach part $partl {
set div 2
for { set i 0 } { $i < $kandl($part) } { incr i } {
set quotienteff($part,$i) [expr {double($stemcijfer($part)) / $div}]
set quotient($part,$i) [format "%7.4f" $quotienteff($part,$i)]
$f.quot$part$i configure -bg gray50
lappend ql [list $quotienteff($part,$i) $stemcijfer($part) $part $i]
incr div
}
}
set ql [lsort -decreasing -command sort_qe_sc $ql]
# Zoek zelfde quotient rond kandmax-de plaats
set qsc [lindex $ql [expr {$kandmax - 1}]]
foreach {mqe msc mpart mi} $qsc { break }
set qscl {}
set cnt 0
foreach q $ql {
foreach {qe sc part i} $q { break }
if { $qe > $mqe || $qe == $mqe && $sc > $msc } {
$f.quot$part$i configure -bg green
set quotient($part,$i) "$quotient($part,$i) ([expr {$cnt + 1}])"
incr cnt
} elseif { $qe == $mqe && $sc == $msc } {
lappend qscl [list $qe $sc $part $i]
}
}
if { [llength $qscl] == [expr {$kandmax - $cnt}] } {
foreach q $qscl {
foreach {qe sc part i} $q { break }
$f.quot$part$i configure -bg green
set quotient($part,$i) "$quotient($part,$i) ([expr {$cnt + 1}])"
incr cnt
}
} else {
foreach q $qscl {
foreach {qe sc part i} $q { break }
$f.quot$part$i configure -bg orange
set quotient($part,$i) "$quotient($part,$i)"
}
}
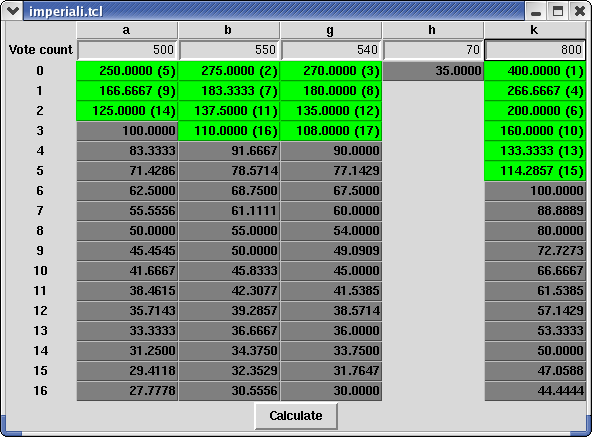
}This is an example when all seats can be allocated:
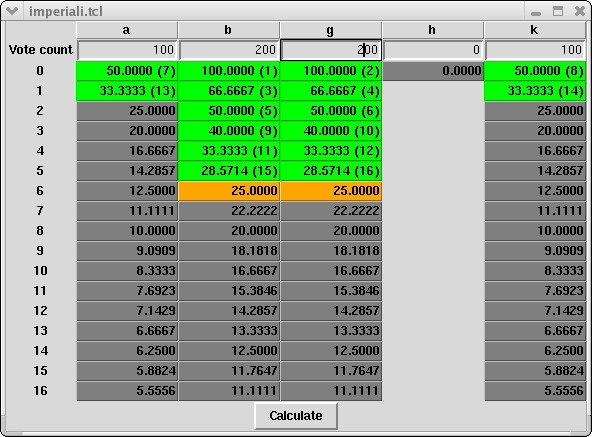
In this example, the last seats still needs to be assigned using the individual vote count or age of the candidates:
Relevant Wikipedia article: http://en.wikipedia.org/wiki/Highest_averages_method