Line Simplification
Keith Vetter 2010-12-17 -- The Douglas-Peucker algorithm [L1 ] is an algorithm for reducing the number of points in a curve by finding a subset that approximates the original curve within a bounded error term.
I needed the algorithm recently when I wanted to download GPS tracks to a GPSr device that had a hard limit to the number of waypoints.
uniquename 2013aug18
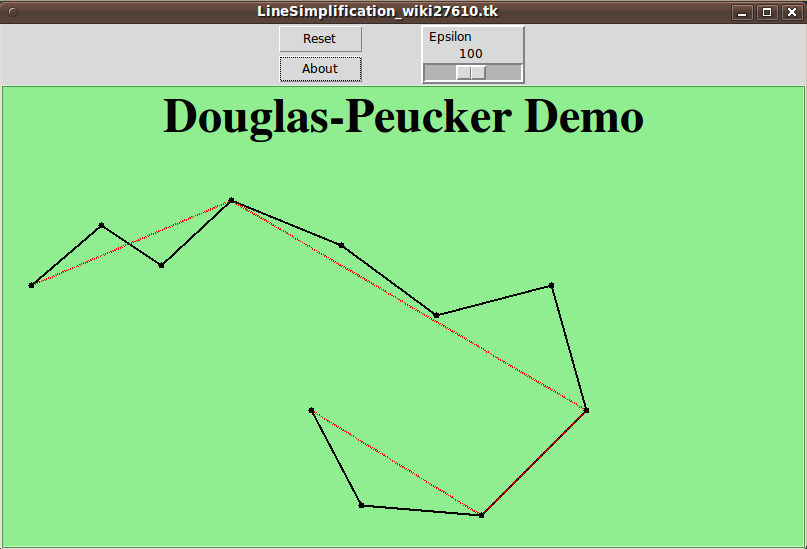
For those readers who do not have the time/facilities/whatever to setup the code below and execute it, here is an image that indicates what the following code can do.
I moved the buttons-frame from the bottom of the GUI to the top, so that the buttons would show on a netbook computer (screen height 600 pixels). I also removed some y-padding (and x-padding) around that frame so that it would not waste y-space.
See the text in the 'About' proc below for an explanation of how to use the GUI and how the algorithm works.
##+##########################################################################
#
# douglaspeucker.tcl -- Implements Douglas-Peucker Line Simplification Algorithm
# by Keith Vetter, Dec 2010
# http://en.wikipedia.org/wiki/Ramer-Douglas-Peucker_algorithm
# http://neonstorm242.blogspot.com/2010/12/douglaspeucker-line-simplification.html
package require Tcl 8.5
package require Tk
set title "Douglas-Peucker Demo"
set P {{50 280} {150 100} {300 150} {450 300}}
set P {{30 200} {100 140} {160 180} {230 115} {340 160} {435 230}
{550 200} {585 325} {480 430} {360 420} {310 325}}
set epsilon 100
proc DouglasPeucker {P epsilon} {
set P0 [lindex $P 0]
set P1 [lindex $P end]
set dmax 0
set idx 0
for {set i 1} {$i < [llength $P]-1} {incr i} {
set d [DistanceToLine [lindex $P $i] $P0 $P1]
if {$d > $dmax} {
set dmax $d
set idx $i
}
}
if {$dmax >= $epsilon} {
set leg1 [DouglasPeucker [lrange $P 0 $idx] $epsilon]
set leg2 [DouglasPeucker [lrange $P $idx end] $epsilon]
set leg [concat [lrange $leg1 0 end-1] $leg2]
} else {
return [list $P0 $P1]
}
}
##+##########################################################################
#
# DistanceToLine
#
# Given a point and a line segment, determines how close that point is
# to that line segment. We drop a perpendicular line and see how far
# along the line segment it is (hdist). If it before or after the line
# segment then we take the euclidean distance, otherwise we take the
# distance along the perpendicular.
#
proc DistanceToLine {P P0 P1} {
lassign $P PX PY
lassign $P0 x0 y0
lassign $P1 x1 y1
set lx [expr {$x1 - $x0}] ;# Line vector
set ly [expr {$y1 - $y0}]
set d [expr {hypot($lx, $ly)}] ;# To normalize line vector
if {$d == 0} { ;# Degenerate line
return 99999
}
set px [expr {$PX - $x0}] ;# Vector to our point
set py [expr {$PY - $y0}]
set hdist [expr {($px*$lx + $py*$ly) / $d}] ;# Distance along line vector
set vdist [expr {($py*$lx - $px*$ly) / $d}] ;# Distance along perpendicular
if {$hdist < 0} { ;# Point behind line segment
set rdist [expr {hypot($px, $py)}]
} elseif {$hdist <= $d} { ;# Point w/i line segment
set rdist [expr {abs($vdist)}]
} else { ;# Point beyond line segment
set px [expr {$PX - $x1}]
set py [expr {$PY - $y1}]
set rdist [expr {hypot($px, $py)}]
}
return $rdist
}
proc Demo {} {
canvas .c -width 800 -height 500 -bd 2 -relief ridge -bg lightgreen \
-highlightthickness 0
frame .f -padx .25i -pady .25i
::ttk::button .reset -text Reset -command Demo:Reset
scale .epsilon -from 10 -to 200 -orient horizontal -command Demo:Show \
-variable ::epsilon -label Epsilon -bd 2 -relief raised
::ttk::button .about -text About -command Demo:About
pack .c -side top -fill both -expand 2
pack .f -side top
grid .reset .epsilon -in .f -padx .25i
grid .about ^ -in .f
.c create text 400 0 -text $::title -font {Times 36 bold} -anchor n -tag title
foreach p $::P {
Demo:DrawPoint {*}$p
}
bind .c <Configure> {Demo:Center %h %w}
bind .c <1> [list Demo:Click %x %y]
bind all <F2> {console show}
}
proc Demo:Reset {} {
set ::P {}
.c delete all
}
proc Demo:Click {x y} {
global P
Demo:DrawPoint $x $y
lappend P [list $x $y]
Demo:Show
}
proc Demo:Center {h w} {
set w [expr {$w/2.0}]
.c coords title $w 0
return
}
proc Demo:DrawPoint {x y} {
set x0 [expr {$x-3}]
set y0 [expr {$y-3}]
set x1 [expr {$x+3}]
set y1 [expr {$y+3}]
set id [.c create oval $x0 $y0 $x1 $y1 -fill black -outline {} -tag dot]
.c bind $id <3> [list Demo:Delete $id $x $y]
}
proc Demo:Delete {id x y} {
global P
set n [lsearch $P [list $x $y]]
if {$n == -1} {
puts "cannot locate $x $y"
return
}
set P [lreplace $P $n $n]
.c delete $id
Demo:Show
}
proc Demo:Show {args} {
global P
.c delete line
if {[llength $P] > 1} {
.c create line [concat {*}$P] -tag line -fill black -width 2
set dp [DouglasPeucker $P $::epsilon]
.c create line [concat {*}$dp] -tag line -fill red -width 2 -dash 1
}
.c raise dot
}
proc Demo:About {} {
set txt "Douglas-Peucker Line Simplification\n"
append txt "demo by Keith Vetter, December 2010\n\n"
append txt "The Douglas-Peucker algorithm is an algorithm for\n"
append txt "reducing the number of points in a curve that is\n"
append txt "approximated by a series of points. It finds a subset\n"
append txt "of points from the original curve that form a\n"
append txt "similar curve.\n"
append txt "\n"
append txt "Demo\n"
append txt "To use this demo, just click on an empty spot to add points.\n"
append txt "Right-click on a dot to remove it. Press Reset to remove all\n"
append txt "points.\n\n"
append txt "Algorithm\n"
append txt "The starting curve is an ordered set of points or lines\n"
append txt "and the distance dimension \u03b5 > 0. \n"
append txt "\n"
append txt "The algorithm recursively divides the line. Initially\n"
append txt "it is given all the points between the first and last\n"
append txt "point. It automatically marks the first and last point\n"
append txt "to be kept. It then finds the point that is furthest\n"
append txt "from the line segment with the first and last points as\n"
append txt "end points. If the point is closer than \u03b5 to the line\n"
append txt "segment then all interior points can be discarded without\n"
append txt "the smoothed curve being worse than \u03b5.\n"
append txt "\n"
append txt "If the point furthest from the line segment is greater\n"
append txt "than \u03b5 from the approximation then that point must be\n"
append txt "kept. The algorithm recursively calls itself with the\n"
append txt "first point and the worst point and then with the worst\n"
append txt "point and the last point.\n"
append txt "\n"
append txt "source:\n"
append txt "http://en.wikipedia.org/wiki/Ramer-Douglas-Peucker_algorithm\n"
tk_messageBox -title "About $::title" -message $txt
}
Demo
return