N-puzzle
Summary
Keith Vetter 2005-12-10 : After writing The Classic 15 Puzzle I decided to write a generalized version that could both play and solve any size board.
I also added some color visualization and made the solving code much cleaner.
Code
##+##########################################################################
#
# N-puzzle.tcl -- Plays and solve the classic N-puzzle for any size board
# by Keith Vetter, Dec 8 2005
#
# Solution algorithm adapted from
# http://www.javaonthebrain.com/java/puzz15/technical.html
#
package require Tk
if {![catch {package require tile} version]} {
if {$version >= 0.5} {
catch {namespace import -force ::ttk::button}
}
}
set S(n,w) 4
set S(n,h) 4
set font Helvetica
if {$tcl_platform(platform) eq "windows"} { set font {Comic Sans MS}}
font create numfont -family $font -size 22 -weight bold
##+##########################################################################
#
# Init -- initializes everything to board size S(n,?)
#
proc Init {} {
global S roundDisp roundDx
set S(n1,w) [expr {$S(n,w) - 1}] ;# Handy constants
set S(n1,h) [expr {$S(n,h) - 1}] ;# Handy constants
set S(n2) [expr {$S(n,w) * $S(n,h)}]
set S(sz) [font measure numfont "15 "] ;# Size of a cell
set S(w) [expr {$S(n,w)*$S(sz) + 1}] ;# Size of board
set S(h) [expr {$S(n,h)*$S(sz) + 1}] ;# Size of board
set S(title) "NM-Puzzle"
set S(state) playing
set S(soln) {}
for {set i 1} {$i <= $S(n2)} {incr i} { lappend S(soln) [expr {$i%$S(n2)}]}
# roundDisp are the offsets walking around a given cell
set t [list -$S(n,w) [expr {-$S(n,w)+1}] 1 [expr {$S(n,w)+1}] $S(n,w) \
[expr {$S(n,w)-1}] -1 [expr {-$S(n,w)-1}]]
MakeArray roundDisp [concat $t $t $t $t]
MakeArray roundDx {0 1 1 1 0 -1 -1 -1 0 1 1 1 0 -1 -1 -1 0 1 1 1 0 -1 -1 -1 0}
}
##+##########################################################################
#
# Resize -- changes the size of the board
#
proc Resize {{whom ""}} {
global S
if {$whom eq "menu"} {
set S(n,w) $S(n)
set S(n,h) $S(n)
}
if {$S(state) eq "solving"} { ;# Are we currently solving???
set S(kill) 1
set S(next) resize
return
}
Init
DoDisplay
NewBoard
}
##+##########################################################################
#
# DoDisplay -- puts up our display
#
proc DoDisplay {} {
global S
if {[winfo exists .c]} {
.c delete all
.c config -width $S(w) -height $S(h)
return
}
bind all <Key-F2> {console show}
wm title . $S(title)
DoMenus
canvas .c -width $S(w) -height $S(h) -highlightthickness 0 -bg gray75
label .msg -textvariable S(msg) -bd 2 -relief ridge
.msg configure -font "[font actual [.msg cget -font]] -weight bold"
pack .c -side top -padx 5 -pady 5
pack .msg -side top -fill x
}
##+##########################################################################
#
# DoMenus -- aren't installing menus really verbose and clunky?
#
proc DoMenus {} {
option add *Menu.tearOff 0
menu .menu
. config -menu .menu
menu .menu.game
.menu add cascade -label "Game" -menu .menu.game
.menu.game add command -label "New Board" -command NewBoard
.menu.game add command -label "Solve" -command Solve
.menu.game add separator
set m .menu.game.size
menu $m
.menu.game add cascade -label "Board Size" -menu $m
foreach n {2 3 4 5 6 7 8 9 10} {
$m add radio -label "${n}x$n" -variable S(n) -value $n \
-command {Resize menu}
}
$m add separator
$m add command -label "Custom..." -command GetSizes
.menu.game add separator
.menu.game add command -label "About" -command About
.menu.game add command -label "Exit" -command exit
}
##+##########################################################################
#
# Draws the board in array B
#
proc DrawNewBoard {} {
global B
.c delete all
for {set row 0} {$row < $::S(n,h)} {incr row} {
for {set col 0} {$col < $::S(n,w)} {incr col} {
set r [TileRect $row $col]
set xy [TileXY $row $col]
set val $B($row,$col)
set tag "tile$val"
set tag2 "cell$val"
if {$B($row,$col) == 0} {
.c create rect $r -width 1 -fill gray75 -tag $tag
continue
}
.c create rect $r -width 1 -fill white -tag [list tile $tag $tag2]
.c create text $xy -text $val -font numfont -tag $tag
.c bind $tag <1> [list Click $val]
}
}
}
##+##########################################################################
#
# NewBoard -- creates a new board in B then draws it
#
proc NewBoard {} {
global B S
if {$S(state) eq "solving"} {
set S(kill) 1
set S(next) "new"
return
}
while {1} {
set b [Shuffle $S(soln)] ;# Pick a random board
if {[IsSolvable $b]} break
}
#set b [ScrambleBoard]
set idx -1
for {set row 0} {$row < $S(n,h)} {incr row} {
for {set col 0} {$col < $S(n,w)} {incr col} {
set val [lindex $b [incr idx]]
set B($row,$col) $val
set B(r,$val) [list $row $col]
}
}
DrawNewBoard
set S(state) playing
set S(msg) ""
}
##+##########################################################################
#
# IsSolvable -- determines if a board is solvable by
# 1. moving hole to solution position
# 2. converting board position into a list
# 3. counting how many swaps needed to get to the solution
# 4. even number of swaps is solvable
#
proc IsSolvable {{lboard {}}} {
global B S
if {$lboard eq {}} { ;# Turn board into a list
set lboard {}
for {set row 0} {$row < $S(n,h)} {incr row} {
for {set col 0} {$col < $S(n,w)} {incr col} {
lappend lboard $B($row,$col)
}
}
}
# Move hole to bottom right position
set hpos [lsearch $lboard 0]
while {$hpos < $S(n2) - $S(n,w)} { ;# Move hole to the bottom
set n [expr {$hpos + $S(n,w)}]
lset lboard $hpos [lindex $lboard $n]
lset lboard $n 0
set hpos $n
}
set lboard [concat [lreplace $lboard $hpos $hpos] 0] ;# Move hole to end
# Count swaps needed to get to solution position
set cnt 0
for {set i 0} {$i < $S(n2)-1} {incr i} {
set who [expr {$i+1}] ;# Who should be in position $i
set n [lsearch $lboard $who]
if {$n == $i} continue
lset lboard $n [lindex $lboard $i] ;# Swap who with piece at $i
lset lboard $i $who
incr cnt
}
return [expr {($cnt % 2) == 0}]
}
##+##########################################################################
#
# Creates a legal random board. To insure legality, it simulates
# moving the tiles MAX times.
#
proc ScrambleBoard {{max 5000}} {
array set DIRS {up {-1 0} down {1 0} left {0 -1} right {0 1}}
set b $::S(soln)
for {set i 0} {$i < $max} {incr i} {
set idx0 [lsearch $b 0] ;# Find the hole
set r0 [expr {$idx0 / $::S(n,w)}]
set c0 [expr {$idx0 - $::S(n,w)*$r0}]
while {1} {
set dir [lindex {up down left right} [expr {int(rand()*4)}]]
foreach {dr dc} $DIRS($dir) break
set r1 [expr {$r0 + $dr}]
set c1 [expr {$c0 + $dc}]
if {$r1 >= 0 && $r1 < $::S(n,h) && $c1 >= 0 && $c1 < $::S(n,w)} break
}
set idx1 [expr {$r1*$::S(n,w) + $c1}]
# Swap idx0 and idx1 in the board
set temp [lindex $b $idx0]
lset b $idx0 [lindex $b $idx1]
lset b $idx1 $temp
}
return $b
}
##+##########################################################################
#
# Shuffle -- shuffles a list
#
proc Shuffle {llist} {
set len [llength $llist]
set len2 $len
for {set i 0} {$i < $len-1} {incr i} {
set n [expr {int($i + $len2 * rand())}]
incr len2 -1
# Swap elements at i & n
set temp [lindex $llist $i]
lset llist $i [lindex $llist $n]
lset llist $n $temp
}
return $llist
}
##+##########################################################################
#
# Moves tiles in response to clicks on the board.
#
proc Click {val {force 0}} {
global B
if {! $force && $::S(state) ne "playing"} return
foreach {row col} $B(r,$val) break
foreach {hrow hcol} $B(r,0) break
set dr [expr {$hrow-$row}]
set dc [expr {$hcol-$col}]
if {$dr != 0 && $dc != 0} return ;# Diagonal move attempt
if {$dr == 0 && $dc == 0} return ;# NOP move attempt
set adr [expr {$dr == 0 ? 0 : $dr/abs($dr)}];# Sign of dr
set adc [expr {$dc == 0 ? 0 : $dc/abs($dc)}]
set len [expr {abs($dr) + abs($dc)}] ;# How many tiles too move
for {set i 1} {$i <= $len} {incr i} {
set r1 [expr {$hrow - $i * $adr}]
set c1 [expr {$hcol - $i * $adc}]
set val $B($r1,$c1)
MoveTile $r1 $c1
UpdateBoard $val 0
}
if {[IsSolved]} Victory
}
##+##########################################################################
#
# MoveTile -- updates data structures for moving a tile
#
proc MoveTile {row col} {
global B
set val $B($row,$col)
foreach {hrow hcol} $B(r,0) break
set B($hrow,$hcol) $B($row,$col) ;# Hole get tile's value
set B($row,$col) 0 ;# Tile is now hole
set B(r,$val) [list $hrow $hcol] ;# Reverse indices
set B(r,0) [list $row $col]
}
##+##########################################################################
#
# UpdateBoard -- updates board to reflect moved tile
#
proc UpdateBoard {val0 val1} {
global B
;# NB. the tiles are ALREADY swapped in B
foreach {x0 y0} [eval TileXY $B(r,$val0)] break
foreach {x1 y1} [eval TileXY $B(r,$val1)] break
set dx [expr {$x1 - $x0}]
set dy [expr {$y1 - $y0}]
.c move tile$val1 $dx $dy
.c move tile$val0 [expr {-$dx}] [expr {-$dy}]
}
##+##########################################################################
#
# Returns TRUE if B is solved
#
proc IsSolved {} {
global B S
set idx 0
for {set row 0} {$row < $S(n,h)} {incr row} {
for {set col 0} {$col < $S(n,w)} {incr col} {
if {[incr idx] != $B($row,$col)} { ;# Always fails for the hole
return [expr {$idx == $S(n2)}]
}
}
}
return 0 ;# Should never get here
}
##+##########################################################################
#
# Shows that you've won
#
proc Victory {} {
.c itemconfig tile -fill magenta
set ::S(state) solved
}
##+##########################################################################
#
# Returns x,y of the center of tile at row,col
#
proc TileXY {row col} {
set x [expr {$col * $::S(sz) + $::S(sz)/2}]
set y [expr {$row * $::S(sz) + $::S(sz)/2}]
return [list $x $y]
}
##+##########################################################################
#
# Returns rectangle of tile at row,col
#
proc TileRect {row col} {
set x0 [expr {$col * $::S(sz)}]
set y0 [expr {$row * $::S(sz)}]
set x1 [expr {$x0 + $::S(sz)}]
set y1 [expr {$y0 + $::S(sz)}]
return [list $x0 $y0 $x1 $y1]
}
proc About {} {
set msg "NM-Puzzle\nby Keith Vetter, December 2005\n\n"
append msg "Lets you create and try to solve the\n"
append msg "classic N-Puzzle. If you have trouble,\n"
append msg "just press the Solve button to see it done."
tk_messageBox -title "About N-Puzzle" -message $msg
}
################################################################
################################################################
#
# Solution code below. Generalized from http://www.javaonthebrain.com
#
proc Solve {} {
global S B MOVES HOLDER
if {$S(state) eq "solving"} { ;# Are we currently solving
set S(kill) 1 ;# Then stop
set S(next) ""
return
}
if {[IsSolved]} { ;# Already solved???
set S(msg) "Already solved"
Victory
return
}
set S(state) solving
set MOVES {}
unset -nocomplain HOLDER
for {set i 0} {$i < $S(n2)} {incr i} {
foreach {row col} $B(r,$i) break
set HOLDER([expr {$row*$S(n,w) + $col}]) $i
}
for {set row 0} {$row < $S(n,h)-2} {incr row} {
SolveRow $row
}
SolveLast2Rows
DoMoves
}
proc Dump {} {
set idx -1
for {set row 0} {$row < $::S(n,h)} {incr row} {
for {set col 0} {$col < $::S(n,w)} {incr col} {
puts -nonewline [format "%3s" $::HOLDER([incr idx])]
}
puts ""
}
}
proc Go {} {
global S B MOVES HOLDER
set MOVES {}
unset -nocomplain HOLDER
for {set i 0} {$i < $S(n2)} {incr i} {
foreach {row col} $B(r,$i) break
set HOLDER([expr {$row*$S(n,w) + $col}]) $i
}
}
##+##########################################################################
#
# SolveRow -- solves any row but the bottom 2. Columns 0 - n-2 are easy,
# the last tow first go vertical then slip right in.
#
proc SolveRow {row} {
global S HOLDER
for {set col 0} {$col < $S(n,w)-2} {incr col} { ;# The easy column
set cell [expr {$row * $S(n,w) + $col}]
set who [expr {$cell + 1}]
AddMessage msg "Putting $who in place"
AddMessage start $who
MoveTo $who $cell
AddMessage done $who
}
set who [expr {$row * $S(n,w) + $S(n,w) - 1}]
set who2 [expr {$who + 1}]
set cell00 [expr {$row*$S(n,w) + $S(n,w) - 2}]
set cell01 [expr {$row*$S(n,w) + $S(n,w) - 1}]
set cell10 [expr {$row*$S(n,w) + 2*$S(n,w) - 2}]
set cell11 [expr {$row*$S(n,w) + 2*$S(n,w) - 1}]
if {$HOLDER($cell00) == $who && $HOLDER($cell01) == $who2} {
AddMessage done $who
AddMessage done $who2
set HOLDER($cell00) -1
set HOLDER($cell01) -1
return
}
AddMessage msg "Putting $who,$who2 in place"
AddMessage start $who
AddMessage start $who2
MoveTo $who $cell01
set hpos [Locate 0]
# Check where $who2 is
if {$HOLDER($cell00) == $who2 && $hpos == $cell11} {
AddMessage msg "Darn! $who2 needs a detour"
MakeDetour {l u r d}
MakeDetour {d l u r d l u r u l d r d}
} elseif {$HOLDER($cell10) == $who2 && $hpos == $cell00} {
AddMessage msg "Darn! $who2 needs a detour"
MakeDetour {r d}
MakeDetour {d l u r d l u r u l d r d}
} elseif {$HOLDER($cell00) == $who2} {
AddMessage msg "Darn! $who2 needs a detour"
MoveTo $who2 $cell10
MakeDetour {r d}
MakeDetour {d l u r d l u r u l d r d}
} else {
MoveTo $who2 $cell11
}
# Now who is in cell01; who2 in cell11
set HOLDER($cell01) $who ;# Unlock this piece
set HOLDER($cell11) -1
MoveTo $who $cell00
AddMessage done $who
set HOLDER($cell11) $who2 ;# Unlock this piece
MoveTo $who2 $cell01
AddMessage done $who2
}
##+##########################################################################
#
# SolveLast2Row -- like SolveRow but works horizontally
#
proc SolveLast2Rows {} {
global S HOLDER
set row [expr {$S(n,h) - 2}]
for {set col 0} {$col < $S(n,w)-2} {incr col} {
set who [expr {$row * $S(n,w) + $S(n,w) + $col + 1}]
set who2 [expr {$row * $S(n,w) + $col + 1}]
set cell00 [expr {$row * $S(n,w) + $col}]
set cell01 [expr {$row * $S(n,w) + $col + 1}]
set cell10 [expr {$row * $S(n,w) + $S(n,w) + $col}]
set cell11 [expr {$row * $S(n,w) + $S(n,w) + $col + 1}]
if {$HOLDER($cell10) == $who && $HOLDER($cell00) == $who2} {
AddMessage done $who
AddMessage done $who2
set HOLDER($cell10) -1
set HOLDER($cell00) -1
continue
}
AddMessage msg "Putting $who,$who2 in place"
AddMessage start $who
AddMessage start $who2
MoveTo $who $cell00
set hpos [Locate 0]
# Check where $who2 is
if {$HOLDER($cell10) == $who2 && $hpos == $cell01} {
AddMessage msg "Darn! $who2 needs a detour"
MakeDetour {d l u r}
MakeDetour {r d l u r d l u l d r u r}
} elseif {$HOLDER($cell11) == $who2 && $hpos == $cell10} {
AddMessage msg "Darn! $who2 needs a detour"
MakeDetour {u r}
MakeDetour {r d l u r d l u l d r u r}
} elseif {$HOLDER($cell10) == $who2} {
AddMessage msg "Darn! $who2 needs a detour"
MoveTo $who2 $cell11
MakeDetour {u r}
MakeDetour {r d l u r d l u l d r u r}
} else {
MoveTo $who2 $cell01
}
set HOLDER($cell00) $who
set HOLDER($cell01) -1
MoveTo $who $cell10
AddMessage done $who
set HOLDER($cell01) $who2
MoveTo $who2 $cell00
AddMessage done $who2
}
# Spin the last 3 pieces into place
set who00 [expr {$S(n2) - $S(n,w) - 1}]
set cell00 [expr {$who00 - 1}]
set who01 [expr {$S(n2) - $S(n,w)}]
set cell01 [expr {$who01 - 1}]
set who10 [expr {$S(n2) - 1}]
set cell10 [expr {$who10 - 1}]
AddMessage msg "Spinning last 3 pieces"
AddMessage start $who00
AddMessage start $who01
AddMessage start $who10
MoveTo $who00 $cell00
MoveTo $who01 $cell01
MoveTo $who10 $cell10
}
##+##########################################################################
#
# MakeDetour -- follows a list of u,d,r&l
#
proc MakeDetour {dirs} {
global S MOVES HOLDER
array set DIRS [list "l" -1 "r" 1 "d" $S(n,w) "u" "-$S(n,w)"]
set hpos [Locate 0]
foreach dir $dirs {
set to [expr {$hpos + $DIRS($dir)}]
set HOLDER($hpos) $HOLDER($to)
set HOLDER($to) 0
set hpos $to
lappend MOVES $to
}
return $MOVES
}
##+##########################################################################
#
# AddMessage -- puts a message into move list to be displayed
#
proc AddMessage {type what} {
lappend ::MOVES [list $type $what]
}
##+##########################################################################
#
# MoveTo -- Moves "piece" to position "to"
#
proc MoveTo {piece to} {
global HOLDER MOVES
set ppath [GetPath $piece $to]
set ppos [Locate $piece]
set HOLDER($ppos) -1
foreach tg $ppath {
MoveHole $tg $ppos ;# Get the hole where we want it
lappend MOVES $ppos ;# Move target into hole
set HOLDER($ppos) 0 ;# Update data structures
set HOLDER($tg) -1
set ppos $tg
}
return $MOVES
}
##+##########################################################################
#
# GetPath -- gets path that "piece" will take to get to "to". How it completes
# this path is somebody elses problem.
#
proc GetPath {piece to} {
set ppath {}
set hpos [Locate $piece]
while {($hpos % $::S(n,w)) < ($to % $::S(n,w))} { ;# Go right if we need to
lappend ppath [incr hpos]
}
while {($hpos % $::S(n,w)) > ($to % $::S(n,w))} { ;# Go left if we need to
lappend ppath [incr hpos -1]
}
while {$hpos > $to} { ;# Get up if we need to
lappend ppath [incr hpos -$::S(n,w)]
}
while {$hpos < $to} { ;# Get up if we need to
lappend ppath [incr hpos $::S(n,w)]
}
return $ppath
}
##+##########################################################################
#
# MoveHole -- the guts of the solution. Figures out how to get the hole to
# the target position next to ppos without disturbing already solved tiles.
#
proc MoveHole {tg ppos} {
global S HOLDER MOVES
global roundDisp roundDx
set hpos [Locate 0] ;# Find the hole
foreach {hrow hcol} [list [expr {$hpos/$S(n,w)}] [expr {$hpos % $S(n,w)}]] break
foreach {prow pcol} [list [expr {$ppos/$S(n,w)}] [expr {$ppos % $S(n,w)}]] break
foreach {trow tcol} [list [expr {$tg / $S(n,w)}] [expr {$tg % $S(n,w)}]] break
# Get in neighborhood of target
while {abs($hcol - $pcol) > 1 || abs($hrow - $prow) > 1} {
if {$hcol < $tcol && $HOLDER([expr {$hpos+1}]) > 0} {
set k [expr {$hpos + 1}]
incr hcol
} elseif {$hcol > $tcol && $HOLDER([expr {$hpos-1}]) > 0} {
set k [expr {$hpos - 1}]
incr hcol -1
} elseif {$hrow < $trow && $HOLDER([expr {$hpos+$S(n,w)}]) > 0} {
set k [expr {$hpos + $S(n,w)}]
incr hrow
} else {
set k [expr {$hpos - $S(n,w)}]
incr hrow -1
}
lappend MOVES $k
set HOLDER($hpos) $HOLDER($k)
set HOLDER($k) 0
set hpos $k
}
# Now we're 1 away from target. Find shortest path to target
if {$hpos == $tg} return ;# Did we get lucky?
# Walk around perimeter of ppos looking for where hpos is
for {set j 8} {$hpos != $ppos + $roundDisp($j)
|| $pcol+$roundDx($j) >= $S(n,w)
|| $pcol+$roundDx($j) < 0} {incr j} {}
# Try going clockwise
set posCount 0
set k $j
while {$ppos + $roundDisp($k) != $tg} {
incr k
set to [expr {$ppos + $roundDisp($k)}]
if {$to >= 0 && $to < $S(n2) && $pcol+$roundDx($k) < $S(n,w) &&
$pcol+$roundDx($k) >= 0 && $HOLDER($to) > 0} {
incr posCount
} else {
incr posCount 50
}
}
# Try going counter-clockwise
set negCount 0
set k $j
while {$ppos+$roundDisp($k) != $tg} {
incr k -1
set to [expr {$ppos + $roundDisp($k)}]
if {$to >= 0 && $to < $S(n2) && $pcol+$roundDx($k) < $S(n,w) &&
$pcol+$roundDx($k) >= 0 && $HOLDER($to) > 0} {
incr negCount
} else {
incr negCount 50
}
}
# Pick optimal direction and do the moves
set dir [expr {$posCount < $negCount ? 1 : -1}]
while {$hpos != $tg} {
incr j $dir
set k [expr {$ppos + $roundDisp($j)}]
lappend MOVES $k
set HOLDER($hpos) $HOLDER($k)
set HOLDER($k) 0
set hpos $k
}
}
##+##########################################################################
#
# Locate -- returns cell in which a given piece is located
#
proc Locate {num} {
for {set i 0} {$num != $::HOLDER($i)} {incr i} {}
return $i
}
##+##########################################################################
#
# DoMoves -- walks our move list and visually does each move
#
proc DoMoves {} {
global S B MOVES
set S(kill) 0
set S(next) ""
set cnt 0
foreach move $MOVES {
if {$S(kill)} break
if {[llength $move] > 1} { ;# Not a move
foreach {type what} $move break
if {$type eq "done"} {
.c itemconfig cell$what -fill green
} elseif {$type eq "start"} {
.c itemconfig cell$what -fill cyan
} else {
set S(msg) $what
}
continue
}
incr cnt
foreach {row col} [list [expr {$move/$S(n,w)}] [expr {$move%$S(n,w)}]] break
Click $B($row,$col) 1
update
after 200
}
set S(state) playing
if {$S(kill)} {
.c itemconfig tile -fill white
set S(msg) "stopped"
if {$S(next) eq "resize"} Resize
if {$S(next) eq "new"} NewBoard
} else {
set MOVES {}
set S(msg) "Done in $cnt move[expr {$cnt > 1 ? "s" : ""}]"
}
}
##+##########################################################################
#
# MakeArray -- turns a list into an array--easier access than lindex
#
proc MakeArray {_var values} {
upvar $_var var
set idx -1
foreach v $values {
set var([incr idx]) $v
}
}
##+##########################################################################
#
# GetSizes -- puts up a dialog to enter new puzzle width and height
#
proc GetSizes {} {
global S
set w .size
destroy $w
toplevel $w
wm title $w "Board Size"
if {[winfo viewable [winfo toplevel [winfo parent $w]]] } {
wm transient $w [winfo toplevel [winfo parent $w]]
}
set S(new,width) $S(n,w)
set S(new,height) $S(n,h)
labelframe $w.f -text "New Board Size" -pady 10
label $w.lwidth -text "Width:"
entry $w.ewidth -textvariable S(new,width) -width 5
label $w.lheight -text "Height:"
entry $w.eheight -textvariable S(new,height) -width 5
grid $w.lwidth $w.ewidth $w.lheight $w.eheight -in $w.f
frame $w.buttons
button $w.ok -text "OK" -command {GotSize 0}
button $w.cancel -text "Cancel" -command {GotSize 1}
grid $w.ok $w.cancel -pady 5 -padx 10 -in $w.buttons
pack $w.f -side top -fill both -expand 1
pack $w.buttons -side top -fill x
wm withdraw $w
update idletasks
set x [expr {[winfo screenwidth $w]/2 - [winfo reqwidth $w]/2 - [winfo vrootx [winfo parent $w]]}]
set y [expr {[winfo screenheight $w]/2 - [winfo reqheight $w]/2 - [winfo vrooty [winfo parent $w]]}]
if {$x < 0} { set x 0 }
if {$y < 0} { set y 0 }
wm maxsize $w [winfo screenwidth $w] [winfo screenheight $w]
wm geom $w +$x+$y
wm deiconify $w
focus $w.ewidth
$w.ewidth icursor end
grab $w
tkwait window $w
}
##+##########################################################################
#
# GotSize -- called when GetSizes dialog is done.
#
proc GotSize {cancel} {
global S
if {$cancel} {
destroy .size
return
}
set emsg ""
if {! [string is integer -strict $S(new,width)] || $S(new,width) < 2} {
set emsg "Bad width value"
} elseif {! [string is integer -strict $S(new,height)] || $S(new,height) < 2} {
set emsg "Bad height value"
} else {
set S(n,w) $S(new,width)
set S(n,h) $S(new,height)
Resize
destroy .size
return
}
tk_messageBox -icon error -parent .size -message $emsg
}
################################################################
################################################################
Init
DoDisplay
NewBoard
returnComments
JAG 11-Dec-2005: Keith, there seems to be a problem with the "Solver" as is depicted in this supposedly "solved" puzzle:
dead link, breaking the link but keeping it: h-t-t-p://www.jeffgodfrey.com/posted_pics/n-puzzle.jpg
KPV oops, somehow the puzzle picked an insolvable starting position. I'm having trouble getting that routine working correctly-- I might have to fall back on just simulating moving the tiles randomly 5,000 times.
KPV 2005-12-12: Now you can play non-square boards, and, hopefully, I fixed the problem of unsolvable starting positions.
uniquename 2013jul29
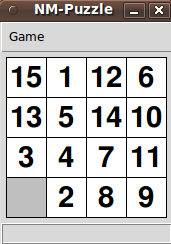
In case the image above at the 'external' jeffgodfrey.com site goes dead, here are a couple of 'locally stored' images of Vetter's GUI. These images show some different aspects of the GUI --- the look on another operating system and the BoardSize menu.
The first image shows what the GUI looks like when it first comes up --- on Ubuntu 9.10 Linux ('Karmic Koala', 2009 October).
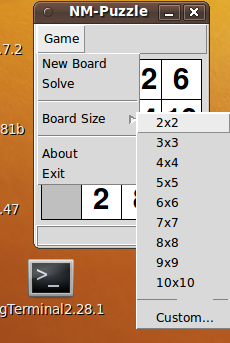
The second image shows how you can use the 'Board Size' menu to choose the MxN size of the game board.
(2013aug16 update: Whoops. I thought Vetter had generalized to handle rectangular boards. I guess I should use the term 'NxN' rather than 'MxN' or 'NM'.)