Old Babylonian Interest Rates and eTCL demo example calculator
Old Babylonian Interest Rates and eTCL demo example calculator, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks,gold9dec2018.
- Old Babylonian Interest Rates and eTCL demo example calculator, numerical analysis
- Sumerian interest rate problem
- Unusual interest rate problems, solution of the silver loan curve (6/5)**N, related? (N*1.2) multiplication table
- Interest Rate Problems Developed from Cuneiform Laws
- Multiplication tablets possibly related? to O.B. interest rates, esp. reciprocal pairs (1_12 and 50)
- Pseudocode and Equations
- Additional reports on Interest Rates
- Growth of a Herd of Cattle in Ten Years
- Table 4. Reconstructed listing of Babylonian Base_60 inverse reciprocals, ref interest rates
- Testcases Section
- Screenshots Section
- figure 1.
- figure 2.
- figure 3.
- figure 4.Solution for small fry, silver loans from 1 to 10 years
- figure 5.Silver loans detail
- figure 6.Linear piece fit of year(N)*(6/5)*(1/2) to Silver loan curve (6/5)**N
- figure 7. Silver loans high scale
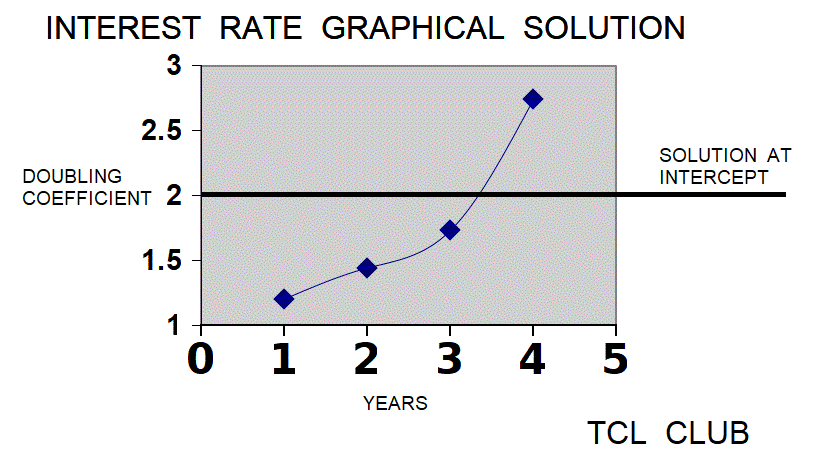
- figure 8. Graphical Solution for Problem
- figure 9. Graphical Solution Extra Chart
- figure 10. Graphical Solution for Grain
- References:
- Appendix Code
- Table for Sumerian interest concept (4/3), modern notation of 33 percent per year
- Table for Sumerian interest concept (6/5), modern notation of 20 percent per year
- Comments Section
Preface
gold9dec2018. Here is some TCL calculations for Old Babylonian interest rates. Most of the testcases involve replicas or models, using assumptions and rules of thumb.
Introduction
In the cuneiform math problems and coefficient lists on clay tablets, there are coefficient numbers which were used in determining the amount of materials and the daily work rates of the workers. In most cases, the math problem is how the coefficient was used in estimating materials, work rates, and math problems. One difficulty is determining the effective magnitude or power of the number coefficient in the base60 notation. In cuneiform, numbers in Base_60 are written using a relative place notation. For example, 20 could represent either 20*3600,20,20/60, 20/3600, or even 1/20. The basic dimensions and final tallies were presented in the cuneiform accounts on clay tablets, but some calculations, some units, some explanations, and some problem answers (aw shucks!) were left off the tablet. The Babylonians did not use algebra notation, decimal notation, errors in percent, or modern units of measurement. So the reader will have to bear some anachronisms in the initial pseudocode preparations and final TCL code. At least one approach for the modern reader and using modern terminology is to develop the implied algebraic equations and decimal equivalents from the cuneiform numbers. Then the TCL calculator can be run over a number of testcases to validate the algebraic equations.
From the cuneiform tablets, the common interest rate for temple or institutional silver was 1/5 or 12/60 per year (360 days), and converted to decimal 0.2 or 20 percent for the calculator. The rule of thumb was for silver to double in 5 years. The common interest rate including default debt obligations for barley or grain was 1/3 or 20/60 per year (360 days), and converted to decimal 0.333 or 33 percent for the calculator. The rule of thumb was for grain at 33.3 percent interest rate to double in 2 years. In some reigns, the harvest tax was 1/2 or 50 percent per annum and possibly listed as default debt interest on the books. In modern terms, the interest rates ranged from 20 to 50 percent. The Babylonian method or "algorithm" was find the total years to double the annual sum of principal and interest, raising the exponent for years of the annual sum to approximate for double or other multiple of the annual product, and interpolate the result for the years less months to double.
Checking TCL Programs with Modern Rule of 70
Both the modern rule of seventy and the rule of seventy two was used to check the Console Program below for Sumerian interest concepts. The rule of 70 is a approximation that gives years to double as dividing 70 by annual percent. Using the 70 rule, the Sumerian rate of 4/3 (P&I) or 33 percent per year should double in expr {70./33} as 2.12 years. Again with the 70 rule, The Sumerian rate of 6/5 (P&I) or 20 percent per year should double in expr {70./20} as 3.5 years. Changing to the 72 rule, The Sumerian rate of 4/3 (P&I) or 33 percent per year should double in expr {72./33} as 2.18 years. The Sumerian rate of 6/5 (P&I) or 20 percent per year should double in expr {72./20} as 3.7 years.
The rule of seventy was used to check the Console Program below for Sumerian interest concepts. The Sumerian rate of 4/3 (P&I) or 33 percent per year should double in 70/20 as 3.5 years. The Sumerian rate of 6/5 (P&I) or 20 percent per year should double in 70/33 as 2.12 years.
Pseudocode and Equations
;# following statements should be pastable into TCL console
;# Alternate and redundant calculations for comparison with
;# approximation results ref. different internet articles and tablets.
;# The Babylonians did not use either algebra, modern equations notation, or interest rates in percent.
;# Babylonians used interest rates expressed in Base_60 rational fractions and Base_60 inverse reciprocals.
set rule_70_problem [/ 70. [* 100. .20 ]] # 3.5 years for doubling amount
set rule_70_problem [/ 70. [* 100. .333 ]] # 2.102 years for doubling amount
set rule_70_problem [/ 70. [* 100. .50 ]] # 1.4 years for doubling amount
set rule_70_problem [/ 70. [* 100. .05 ]] # 14.0 years for doubling amount
set ln_rule_problem [/ [log 2. ] [* 1. .2 ] ] # 3.4657 years for doubling amount
set ln_rule_problem [/ [log 4. ] [* 1. .2 ] ] # 6.931 years for 4X amount
set ln_rule_problem [/ [log 2. ] [* 1. .333 ] ] # 2.0815 years for doubling amount
set ln_rule_problem [/ [log 4. ] [* 1. .333 ] ] # 4.1630 years for 4X amount
;# The rule of 70 and rule of 72 are approximations, not exact results.
set rule_72_problem [/ 72. [* 100. .20 ]] # =~ 3.6 years for doubling amount
set rule_72_problem [/ 72. [* 100. .333 ]] # =~ 2.162 years for doubling amount
set rule_72_problem [/ 72. [* 100. .50 ]] # =~ 1.44 years for doubling amount
set rule_72_problem [/ 72. [* 100. .05 ]] # =~ 14.4 years for doubling amount
;# begin Babylonian issues
;# The Babylonians did not use interest rates in percent.
;# Babylonians used interest rates expressed in Base_60 rational fractions and Base_60 inverse reciprocals.
;# B. interest rates are expressed relative to 60 or 60 parts in silver or grain.
;# B. silver of thumb was < silver doubled in 4 years. >
;# B. silver I equals 1/5 in rational fractions (= .2 decimal)
;# B. silver P&I equals 6/5 or 1+1/5 (= 1.20 decimal)
set sum [+ 1. 0.2 ] # answer decimal 1.2
set months [* 12. [/ [- [** 1.2 4. ] 2. ] [- [** 1.2 4. ] [** 1.2 3. ] ] ]] # 2.555 less months of 30 days
set babylon_problem [** 1.2 3. ] # answer decimal 1.7279
set babylon_problem2 [** 1.20 4. ] # answer decimal 2.0736
set sumer_problem [** [/ 4. 3. ] 7. ] # answer decimal 7.49154
set babylon_problem [** 1.2 3. ] # answer decimal 1.7279, P&I after 3 years
set babylon_problem2 [** 1.2 4. ] # answer decimal 2.0736, P&I after 4 years
;# B. rule of thumb was < grain doubled in 2 years.>
;# B. grain I equals 1/3 in rational fractions (= .3333 repeating decimal)
;# B. grain P&I equals 4/3 or 1+1/3 (= 1.3333 repeating decimal)
set sumer_problem [** [/ 4. 3. ] 7. ] # answer decimal 7.49154
;# inverse problem, speculative formulas, what was interest rate from doubling time?
set sumer_problem2? [ expr { 72./2.1818 } ] ;# answer 33 percent decimal
set sumer_problem3? [ expr { 72./(100.*2.1818) } ] ;# answer 0.3333 decimal =~ Babylonian fraction 1/3
set sumer_problem4? [ expr { 72./(100.*3.4657) } ] ;# answer 0.207 decimal =~ Babylonian fraction 1/5, B. P&I = 6/5 rational fraction
;# curious coincidence? that the inverse of B. silver P&I (R_ 6/5) equals 72
set inverse_P&I? [ expr { 60./(5./6.) } ] ;# answer 72
;# multiplication tables of 5/6 * N have been found,
;# but no obvious uses of 72 on interest problem tablets.
Testcases
The answer for the first testcase was between 3 years for 1.7279 factor and 4 years for 2.0736 factor, see above eTCL statements. The Babylonian solution interpolated between 3 and 4 years for the factor of 2, giving the answer in months short of 4 years.For comparison, the modern lump sum formula for 20 percent at 3.8 years gives factor 1.99. The second testcase was finding the doubling time at 33 percent interest rate. The answer for the second testcase was between 2 years for 1.7689 factor and 3 years for 2.3526 factor. The Babylonian method would interpolate between 2 and 3 years for the factor of 2, giving the answer in months short of 3 years. For comparison, the modern lump sum formula for 33 percent at 2.488 years gives factor 1.908 .The third testcase was finding the doubling time 50 percent interest rate. The answer for the third testcase was between 1 year for 1.5 factor and 2 years for 2.25 factor. The Babylonian method would interpolate between 1 and 2 years for the factor of 2, giving the answer in months short of 2 years. For comparison, the modern lump sum formula for 50 percent interest at 1.7 years gives factor 1.992 .
Its clear that the Babylonian interpolation is pretty sophisticated, several rule of three trials with a single post did not give reliable estimates. eval 4.*(2./2.0736) gives 3.8580. eval 4*1.7279/2. gives 3.4558. Ref. paper of Donald Knuth.
Some testcases were developed to check the lump sum formula in the eTCL calculator. For fifth testcase, the modern lump sum formula for principal of 1 and 12 percent interest at 7 years gives amount of 7.5 .For sixth testcase, the modern lump sum formula for principal of 1000 and 15 percent interest at 3 years gives amount of 1520. For seventh testcase, the modern lump sum formula for principal of 1000 and 33 percent interest at 5 years gives amount of 4208.
Open Office Spreadsheets for Compound Interest Rates for Silver and Grain
Open Office Spreadsheets. To simplify typical problems, the Babylonians would normalize the base quantity ( principal here) to unity ( 1 ) and it was silently understood that 1 = 60 parts and 1 = 60/60 in the base60 notation. For example, the Open Office Spreadsheets below are really dealing with a normalized one dollar in USA currency and decimal units, but the normalized one could apply to one gur of grain (300 liters), one shekel of silver, or one ounce of silver dollar. As understood here, the specific end balance in silver or kind over N years equals principal in amount deposit units * (normalized end balance over N years for interest rate). For example in Babylon, the original loan in kind might be 20 calves over 10 years at P&I = (1+1/5) or 20 percent per annum. The specific end balance from the normalized end balance of 6.1917 in the spreadsheet would be expr { 20* 6.1917} or 123.834 decimal calves. Don't laugh, the Sumerian word for interest is "mas" and means calf or young beast, reflecting the natural increase in herds of cattle. Even though these spreadsheets are in decimal notation, its fairly easy to mentally change the principal from 1 to 60 for base60 fractions, just as the Babylonian mathematicians did. The decimal parts were run out 6 places, so each normalized line in the Open Office spreadsheets can be used to check the calculator results in most Babylonian interest problems or even cattle herd increase.
Even though these Open Office spreadsheets are in decimal notation, its fairly easy to mental change 1 to 60 for base60 fractions, just as the Babylonian mathematicians did. The decimal parts were run out 6 places, so each normalized line in the Open Office spreadsheets can be used to check the calculator results. One supposes that the Babylonian would begin looking at the close matches to the geometric series { 1X,2X,4X,8X,16X,32X,64X} in the silver interest table, as representing powers of 2. Whereas I in the Western mindset look for close matches to the mixed sequence { 10X,50X,100X,1000X} in the grain interest table, as representing powers of 10. But that is the difference between the former genius and the later peanuts.
Sumerian interest rate problem
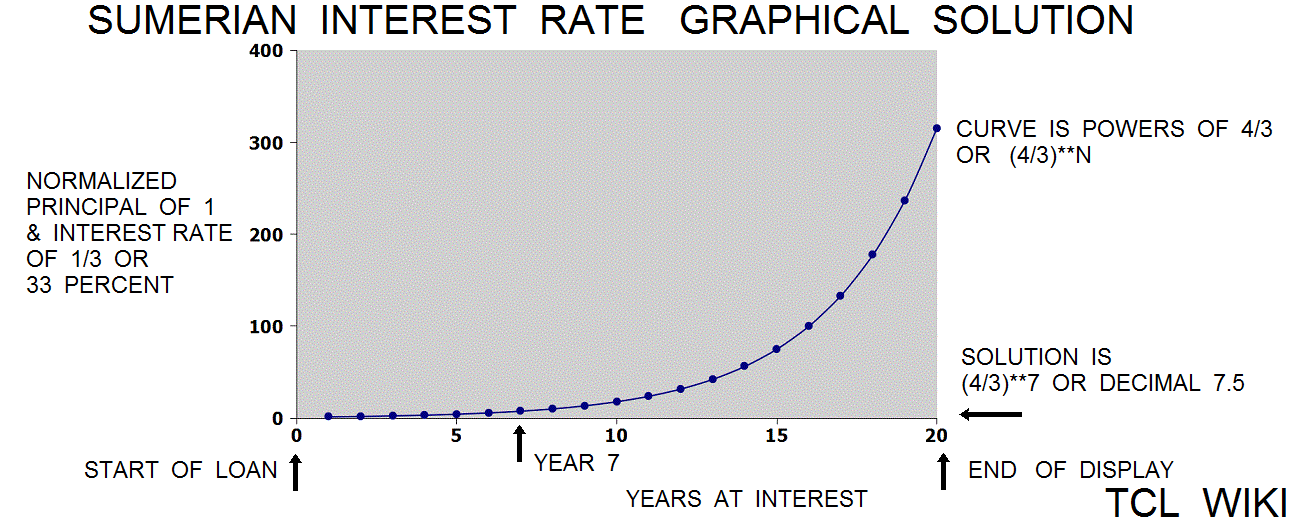
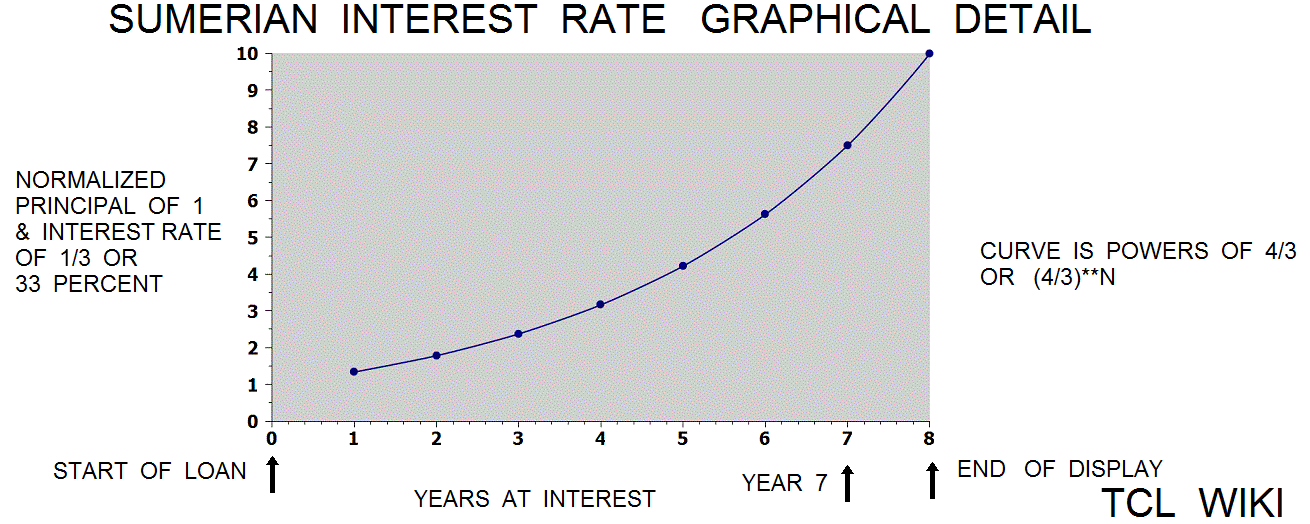
Leaving aside the Old Babylonian era, Muroi proposed a solution to a Sumerian interest rate problem or reference to a grain loan. This discussion uses modern terms like principal, percent, and function for tutorial convenience. For the solution using normalized numbers, the principal was factored out or assigned as 1. For the first year, the total return would be $principal * (1+1/3), where 1 represents the principal and the term 1/3 represents 33 percent interest per year. The function or curve of total return would be (4/3)**N, where N is number of years. The solution for 7 years was (4/3)**N, substituting (4/3)**7 or rounded 7.5 decimal years, written as 7+30/60 years in base60 notation. Through not found in the texts, a list of (4/3)**N powers would effectively be an interest rate table.
Unusual interest rate problems, solution of the silver loan curve (6/5)**N, related? (N*1.2) multiplication table
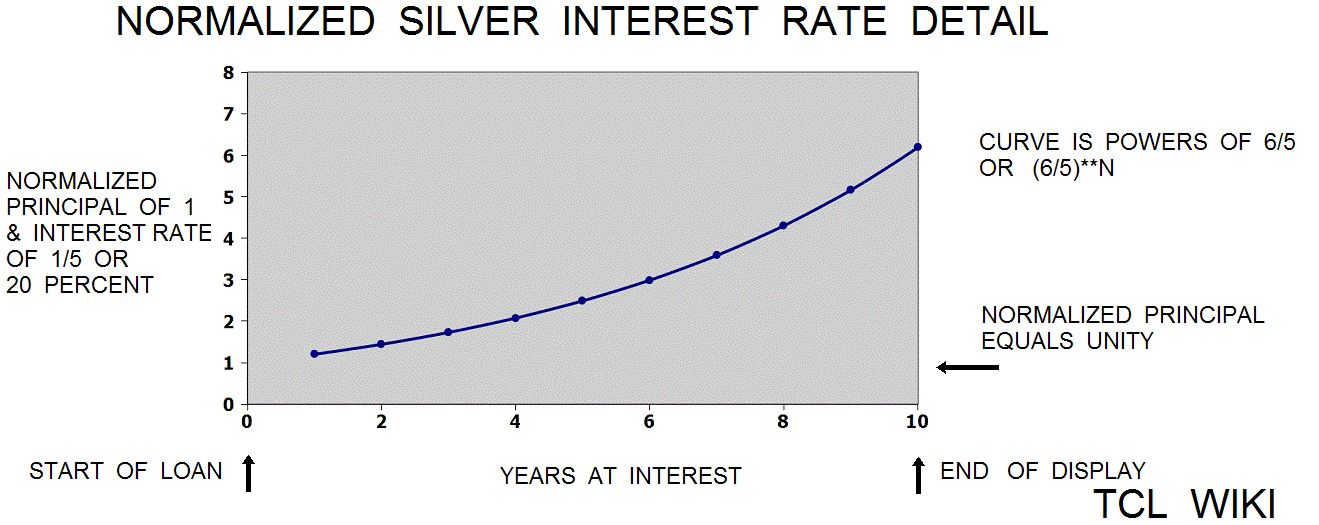
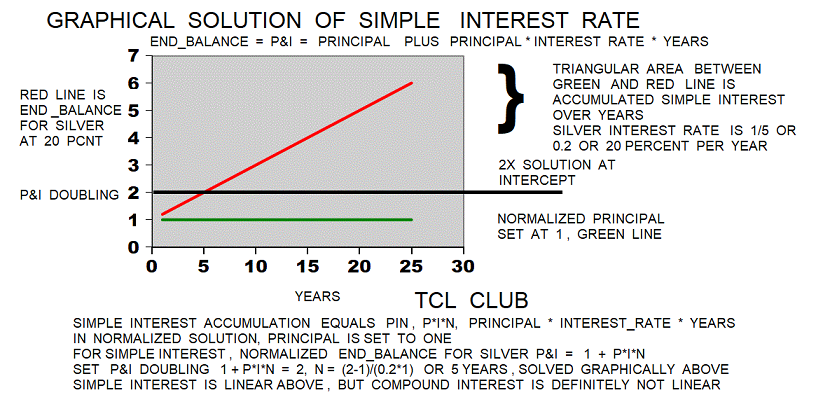
Friberg and Muroi discussed tablet VAT8521 with unusual interest rate problems. The 4 problems and the solution numbers were given on the tablet VAT8521 without the Bablylonian method. The silver interest rate of (1+1/5) or (6/5) is being used to find the capital from interest amounts given as squares, cubes, and quasi-cubes. Using modern notation, these solutions can be located on the silver loan function, as (6/5)**N. These problems were probably solved as simple_interest. Possibly the (N*1.2) multiplication table is a related tablet to the silver loan curve.
The formula for simple interest is simple_interest = principal *interest_rate* time_in_years, where years or intervals of time must agree. Interest rate by month or quarter year is also possible in Babylonian records. Rearranging terms, principal = simple_interest / (interest_rate* time_in_years). Also from rearrangement, (interest_rate* time_in_years) = simple_interest/ principal. In Babylonian mathematics division was handled with reciprocals, so reciprocals could either used as a look up table or taken reciprocals might appear in the tablet calculations. Switching to the reciprocation method , the formula for principal might be revised as principal = simple_interest *(1/ (interest_rate* time_in_years)). The formula for (interest_rate* time_in_years) might be revised as , (interest_rate* time_in_years) = simple_interest *(1/ principal). Also it follows that time_in_years = simple_interest *(1/ principal)*(1/interest_rate).
gold 2Dec2018. The VAT8521 problems are setting mathematical functions of squares, cubes, and quasi-cubes equal to an interest rate, or effectively the interest rate function. After looking at these Babylonian problem statements for several years, it is difficult to understand the purpose of these statements on interest. In opinion, most Western readers get a nonpulsed reaction at squares, cubes, and quasi-cubes set equal to an interest rate . In fact, these problems look almost like riddles and something to shake the mind of the student. However, a good part of cuneiform mathematics is units conversion and conversion from one measure to another measure. Possibly, the Babylonian mathematician is implying that the mathematical functions of squares, cubes, and quasi-cubes ae related or convertible to the interest rate functions., examples (6/5)**N, (4/3)**N, and 2**N.
Using modern formula notation for simple_interest and base10 conversion to solve O.B. problems on tablet VAT8521. ref Friberg for exact translation.
Pseudocode and Equations
1) interest = decimal 100, initial capital= decimal 500. principal = simple_interest *(1/ (interest_rate* time_in_years)), substituting principal = expr (100. * (1./(.2*1.))), 500. 2) interest = cube of 30, decimal 27000, principal = decimal 135000. principal = simple_interest *(1/ (interest_rate* time_in_years)) substituting principal = expr (27000. * (1./(.2*1.))), reduction principal = expr (27000. * 5. ), decimal 135000. 3) interest = square of 6, decimal 36, principal = decimal 180. principal = simple_interest *(1/ (interest_rate* time_in_years)) substituting, principal = expr (36. * (1./(.2*1.))), reduction, principal = expr (36. * 5. ), decimal 180. 4) interest = quasicube of 3, decimal 18, principal = decimal 90. principal = simple_interest *(1/ (interest_rate* time_in_years)) substituting, principal = expr (18. * (1./(.2*1.))) reduction, principal = expr (36. * 5. ), decimal 180.
Interest Rate Problems Developed from Cuneiform Laws
In the history of cuneiform mathematics, the most sure dating is given by royal degrees, laws, and court decisions. In the Laws of Ur-nanna, the equivalent rate of 20 percent per year is given for both grain and silver. However, the bulk of the tablets over different eras give a rate of 33.33 for grain. The analysis is uncertain whether the Laws of Ur-nanna refer either to simple interest or compound interest. The Old Babylonian interpolation between powers of two was for compound interest. A short TCL procedure was written to compute a simple_interest_rate from the principal and interest given in the laws.
Short TCL Procedure for Simple Interest Rate
proc simple_interest_rate { simple_interest_amount principal time_in_years } {
proc simple_interest_rate { simple_interest_amount principal time_in_years } {
return [ expr { $simple_interest_amount*100.*(1./$principal)*(1./$time_in_years)} ] }
puts " [simple_interest_rate 100 300 1 ] percent " #33.333 percent
puts " [simple_interest_rate 2 10 1 ] percent " # 20.0 percent
puts " [simple_interest_rate 60 300 1 ] percent " # 20.0 percent Pseudocode and Equations
5) Laws of Ur-nanna were for a loan of 1 gur =300 liters grain for one year, had interest of 1 barig 4 ban= 1*60+4*10=100 liters. Problem 2 of tablet YBC4698 had the exact same numbers. Interest treated apparently as lump sum, not exactly an interest rate as interest per time interval. interest_rate = simple_interest *(1/ principal)*(1/time_in_years) interest_rate = expr (100.*(1./300.)*(1./1.)) interest_rate = 0.33 or 100*0.33, 33 percent 6) Laws of Ur-nanna had for a loan of 10 shekels of silver, the interest for 1 year shall be 2 shekels. interest_rate = simple_interest *(1/ principal)*(1/time_in_years) interest_rate = expr (2.*(1./10.)*(1./1.)) interest_rate = 0.20 or 100*0.20, 20 percent 7) Problem 1 of tablet YBC4698l had loan of 1 gur =300 liters grain for one year, had interest of 1 barig = 1*60 =60 liters. Ref. Middeke-Conlin and Proust interest_rate = simple_interest *(1/ principal)*(1/time_in_years) interest_rate = expr (60.*(1./300.)*(1./1.)) interest_rate = 0.20 or 100*0.20, 20 percent
Specific Problem on Clay Tablet YBC-4669-rev
The clay tablet YBC-4669-rev was translated by Neugebauer and further discussed by Friberg and Al-Rawi. The interest amount is cited at one gur and the question is when or how many years will the principle equal the interest amount. If the interest amount = principal = one gur, then the P&I = 1+1 or 2 at the end of the last year. No method or answer result for the interest rate problem is given on the tablet, but a oneliner procedure was written in TCL. Since no interest rate is specified, presumably the interest rate is the silver rate at 20 percent interest. However, since the text specifies gur as a grain measure, there is a possibility that either the grain rate of 33 percent interest is meant or some other unknown rate to the modern reader. Although no answer is specified, it is desirable to establish boundaries on the problem using the rules of thumb, TCL code, and redundant methods. With trial and error method, the doubling formula equals expr (1+12./60.)*(1+12./60.)*(1+12./60.)*(1+12./60.) = 2.0736, where the answer is somewhat less than 4 years. To simplify typical problems, the Babylonians would normalize the base quantity ( principal here) to unity ( 1 ) and it was silently understood that 1 = 60 parts and 1 = 60/60 in the base60 notation. Using the silver interest rate of 20 percent, an iterative solution is possible with procedure modern_formula_lump {1 .2 2} , succession modern_formula_lump{ 1 .2 3}, succession modern_formula_lump {1 .2 4}, where the approximate answer is 2.0736, roughly doubling in 4 years. An exact solution would be to interpolate between year 3 and year 4, as the TCL calculator does. As an alternate method, the TCL calculator with {1,.2,2} gives approximately 3 years, 9.5 months or 4 years rounding. Even considering the inadequate information, the problem in YBC-4669-rev is very similar to Testcase 1 already loaded in the TCL calculator.
Continuing with the clay tablet YBC-4669-rev as translated by Neugebauer. The interest rate problem is outlined in the text and the Babylonian answer is given as 34_43_20 base60. Asking for the silver principal, the givens are total Principal and Interest P&I was one shekel or one gin of silver. The term of loan was 3 years. In Babylonian terms, the interest payment were given as 1 mina per 12 shekels, the reciprocal of modern usage or expressions. In modern terms and inverted, the interest rate was 12 shekels over 60 shekels per year and would be expr { 12./60 }, 0.2 decimal, 20 percent. The Babylonians did not use percent, but the interest in percent is the most convenient form for the modern reader. The hand calculation in decimals is P&I = expr / 60. [* $principal [** [+ 1. $interest $year ]], expr { / 60. [* 1. [** [+ 1. .2 3. ]] }, 34.7222 decimal, converts to 34_43_20 base60. The term 60 is a units conversion. The numbers on the tablet are given in relative place value in base60 notation, so some problem boundaries are useful for checking absolute values of the base60 notation. The check on the boundaries of problem would be that the principal must be less than one shekel. The Babylonian rule of thumb is that silver doubles is two years. If 2*P equals 1 shekel in two years (reductio ad absurdam), then the answer for the interest problem for over three years must in range of a half shekel, 30/60 shekel. While the method was not on the tablet, the formula term (1+12/60)**year is a probable expression for the silver P&I and is considered a use for the Babylonian square and cube tables.
Pseudocode and Equations
proc modern_formula_lump {principal interest year } {return [* $principal [** [+ 1. $interest] $year ]]}
modern_formula_lumpx {principal interest year } {return [/ 60. [* $principal [** [+ 1. $interest] $year ]]]}
# usage is modern_formula_lumpx 1. .2 3 # answer 34.7222 decimal , equivalent base_60 is 34_43_20
modern_formula_lump 1 .2 2 # answer 1.44
modern_formula_lump 1 .2 336 # answer 1.7279
modern_formula_lump 1 .2 4 # answer 2.0736 Any Babylonian Simple Interest Tables?
What would a Babylonian table of simple interest look like? For simple interest, the modern text book formula is the end_balance equals P*n*t, where P is principal,n=interest_rate, and t=time. Another formula for simple interest with spelled out variables is end_balance = principal*interest_rate*year. Lets use the Babylonian math trick of setting the base quantity or principal here equal to one, so the simple interest formula simplifies to normalized end_balance equals 1*interest_rate*year. Meaning, normalized end_balance equals interest_rate*year. The Babylonians did not use percent per annum, but an integer fraction examples like (1/3),(1/5),(20/60), or (12/60) as a factor or interest rate. The Babylonians might have made tables of normalized principal plus interest P&I such that the tables would contain either (1+1/5), (1+1/3) or their base60 reciprocals. So an example table of normalized end_balance = 20/60*sequence_years (1,2,3,4...N) or look like some of the numerous “Babylonian single multiplication tables” that have been found on clay tablets.
Multiple formulas from end_balance = principal*interest_rate*year. Rearranging terms, principal = end_balance /( interest_rate*year). Rearranging terms, interest_rate = end_balance /( principal*year). Rearranging terms, year = end_balance /( principal*interest_rate).
Continuing, the Babylonians used base60 reciprocals in their calculations, so some simple interest tables might take the form of reciprocal_base60 * sequence_years (1,2,3,4...N). The key cuneiform terms for principal plus interest P&I in normalized form are silver expr { 60./(1+1./5)} = 50.0 and grain expr{ 60./(1+1./3)} = 45.0. The equivalent reciprocal pars are {(1+12/60),50.} and {(1+20/60),45}. Multiplication tables have been reported for 48,50,80,90 etc in equivalent decimal notation. Some tables are written such that the factor numbers are given as {1*c,2*c,3*c,...19*c,20*c,30*c,40*c,50*c ... }. Note the use of decades in mixed sequences {1,2,3,4,...N...N*10}. In opinion, some multiplication tables are unusual evidence of base10 factors and calculations in Babylonian tables. Not saying that all Babylonian single multiplication tables were used for calculations of simple interest, but there is a possiblity that some Babylonian single multiplication tables were used for simple interest rate calculations and P&I.
Maybe numerical coincidence, but the reciprocal pairs for cuneiform P&I {(1+1/5),50 } and {(1+1/3.), 45 } are the first and third in the standard reciprocal list, respectively. In the combined multiplication tables, 50 and 45 are the first and third in the header or index lists. Lets examine equivalent expressions for 50 and 45 in the multiplication tables. The multiplication table for 50 would have sequence {1*c,2*c,3*c,4*c...10*c,20*c, 30*c...}, and substituting for 50 {1*50,2*50,3*50,4*50...10*50,20*50, 30*50...}. The base60 reciprocal for 50 is equivalent (60/(1+1/5)), and substituting {1*(60/(1+1/5)),2*(60/(1+1/5)),3*(60/(1+1/5)),4*(60/(1+1/5))...10*(60/(1+1/5)),20*(60/(1+1/5)), 30*(60/(1+1/5))...}. The multiplication table for 45 for the grain P&I (1+1/3) would have equivalent sequence {1*(60/(1+1/3)),2*(60/(1+1/3)),3*(60/(1+1/3)),4*(60/(1+1/3))...10*(60/(1+1/3)),20*(60/(1+1/3)), 30*(60/(1+1/3))...}. So the multiplication lists for 50 and 45 has reciprocal factors for cuneiform P&I built into the list. The calculation for doubling for simple interest at 20 percent per year in 5 years is end_balance = expr {1+1*.2*5}= 2 . For two years simple interest end balance equals expr {1+1*.2*2} = 1.4 and compound interest end_balance equals expr {(1+1./5)*(1+1./5) } = 1.44 . 4*(1/(1+1./5))
Multiplication tablets possibly related? to O.B. interest rates, esp. reciprocal pairs (1_12 and 50)
The multiplication tablet MS3866 contains a multiplication of 1_12 (base60) for numbers 1 through 23 and has the multiplication (square) of 1_12*1_12, ending at midtablet on the obverse. Since the number sequence ends at midtablet and not with the tablet broken off, the analysis can be sure that the sequence is complete and ends with a square at the end. The term ara (trans. area, multiply area, or multiply step) is used for each of the 23 multiplication operations and also for the square expression. Reading a lot into bare numbers, but 1 to 23 could be interpreted as the factor for either 23 years or 23 months. The square 1_12*1_12 on the tablet could be interpreted as the factor for a silver loan of two years or 24 months, (1+1/5)**2. Referencing the early Sumerian period, the tribute of military clans was on a lunar calendar or 18 month basis, so possibly an interest table of return by month would make more sense than yearly interest. Also for the common man or overseer in Sumerian times, laws and court decisions rarely reference more than one year loans ... inferring a loan ( of seed grain or other ) was repaid in kind or on the books from the coming or next harvest. The number is 1_12 in base sixty, but is equivalent to (1+12/60), (1+1/5), or decimal 1.2. The reciprocal is 1/1.2 or decimal 0.8333 which had alternate expressions in base60 notation as 50/60, special fraction 5/6, or 5. The numbers 1_12 and "50" are reciprocal pairs. Multiplication tables for "5" and "50" have been found, ref CMT. This tablet might be associate to the factor (interest_rate* time_in_years). Maybe numerical coincidence, but the expression year(N)*(6/5)*(1/2) was a partial linear piece fit to the curve (6/5)**N. A table of the reciprocals for (1/ (interest_rate* time_in_years)) would be useful to a Babylonian scribe. However, one can have the evidence of this tablet MS3866, but the use of this tablet as an interest table or interest rate calculations is not proved. Additional Ref Ni2739, possible 1_12? in multiplication table from Nippur (Neugebauer, MKT 1 (1935).
In some scribal traditions and not very consistent, the last calculation on a math table or math problem tablet was an error check and contained the known solution to the problem. If one argues that the solution on tablet MS3866 is decimal 1.2**2, 1.44, or 2 years of compound interest, then the "multiplication step table" of 1_12 multiplication should lead to that conclusion. Given the best documentation from the other tablet ( involving interpolation of powers of 2), then the bare numeric solution to the problem (1.44) lies between line 1 of 1.2 and line 2 of 2.4. In other terms, the numeric solution is (1.44-1.2/(2.4-1.2), reduction (.24/1.2), decimal 0.2 or 12/60 past line one. Kind of a circular argument, but possibly narrowing down the purpose of the tablet MS3866. A fudge formula was found that the formula Year*(6/5)*(1/2), Year*(6/10), or Year*(36/60) is a linear fit to the exponential (6/5)**N over about the first ten years. The Babylonian reciprocal would be 60/36 or 1+40/60.
Pseudocode and Equations
# using pseudocode
# possible problem instances
# alternate solution
seek doubling time in years for 20 percent per year, meaning 1.2 for P&I
Babylonians had 360 days in year, modern 365 days might be an issue???
4.*(2./2.0736) = 3.858 years
rule of 70 approx. 70/20 or 3.5 years
log solution, y = [/ [log 2. ] [log 1.2]]
exact log solution is 3.8017840169239308 years, rounds to 3.802 years
[* 2. [/ [ * 1.2 1.2 1.2 1.2 ] [* 1.2 1.2 1.2 ] ]] = 2.4
[** 1.2 1.] = 1.2
[** 1.2 2.] = 1.44
[** 1.2 3.] = 1.7279
[** 1.2 4.] = 2.0736
scribe answer
interpolate between
expr 1. + 43./60.+ 40./3600. decimal 1.727777777777777
expr 2. + 4./60.+ 25./3600. decimal 2.073611111111111
to find 3+47/60+ 13/3600+ 20/216000 decimal 3.787
[+ 3. [/ [- 2. [ ** 1.2 3. ] ] [- [** 1.2 4. ] [ ** 1.2 3. ]]]]
decimal 3.787037037037037 years
----
seek doubling time in years for 33 percent per year, meaning 1.33 for P&I
3.*(2./2.37037)= 2.531 years
log solution, y = [/ [log 2. ] [log [+ 1 [/ 1. 3.]]]]
2.4094208396532095 years
rule of 70 approx. 70/33 or 2.12 years
[** [+ 1. [/ 1. 3.]] 1.] =1.3333333333333333
[** [+ 1. [/ 1. 3.]] 2.] =1.7777777777777777
[** [+ 1. [/ 1. 3.]] 3.] =2.37037037037037
[** [+ 1. [/ 1. 3.]] 4.] =3.160493827160493
[** [+ 1. [/ 1. 3.]] 5.] =4.213991769547324
[** [+ 1. [/ 1. 3.]] 6.] =5.618655692729765
[** [+ 1. [/ 1. 3.]] 7.] =7.491540923639686
[** [+ 1. [/ 1. 3.]] 8.] =9.98872123151958
seek Muroi solution of P&I*N of 7.5 with solution of 7 years
8*(7.5/8)=7.5 ????
8*(7.5/9.98)= 6.012 ????
7*(6/5.6)= 7.5
7.5*(5.6/6)= 7 years
7 years over 7.5 P&I result is 5.6 result over 6 years
xxx years over 7.5 P&I result is 5.6 result over 6 years
log solution, y = [/ [log 7.5 ] [log [+ 1 [/ 1. 3.]]]]
7.003922779651095 years
inverse proportions here
# testing powers of 16. Yes, this is a B. Logarithm table!
Using modern formulas and decimal notation here.
[** 16. [/ 1. 1.] ] = 16.0
[** 16. [/ 1. 2.] ] = 4.0
[** 16. [/ 1. 4.] ] = 2.0
[** 16. [/ 1. 8.] ] = 1.4142135623730951
[** 16. [/ 1. 16.] ] = 1.189207115002721
possibly 16**N used in quad., weight riddles, or interest problems
but not sure how ??? There is B. table of this.
how many years for x rate to double , log solution, y = [/ [log 2. ] [log [+ 1 [/ 1. 3.]]]]
how many years for x rate to 4x, log solution, y = [/ [log 4. ] [log [+ 1 [/ 1. 3.]]]]
how many years for x rate to 8x, log solution, y = [/ [log 8. ] [log [+ 1 [/ 1. 3.]]]]
how many years for x rate to 16x, log solution, y = [/ [log 16. ] [log [+ 1 [/ 1. 3.]]]]Additional reports on Interest Rates
In modern terms, loans of silver at 16.666 percent and 25 percent have been reported in Late Babylon. 16.666 percent was equivalent to factors in base60 as (1+10/60) and (1+1/6) and reciprocal 6. 25 percent was equivalent to factors in base60 as (1+15/60) and (1+1/4) and reciprocal 4. The factor (1+15/60) and 48 is the reciprocal pair related to the 48 multiplication table. The factor 1_20 (1+20/60) and 50 is the reciprocal pair related to the 50 multiplication table. Silver loans were reported at 6.25 percent. 0.0625= (1+ 3/60+45/3600) or rounded 4/60. Reciprocal pairs are 1_4 or (1+4/60), and 56+15/60.
gold 6/6/2021. updated prose.The Late Babylon interest rate of 16.666 percent converts to expr { (1+16.66/100.)*60 }, 1_10 base_60 P&I. The inverse is expr { 60. / (1+10/60.) }, 51.4. The Late Babylon interest rate of 25 percent converts to expr { (1.+25./100.)*60 }, 1_15 Base_60 P&I, rounded. The inverse is expr { 60. / (1+15/60.) }, 48.0
gold 6/6/2021. updated prose. We have really good info on ancient Greek period. But the character of loans had changed to "rich" individuals rather than institutions (temples and state), I think.
369 B.C. Greek man borrowed on multiple dwellings at 16%, similar rate to Late Babylon quote 346 B.C. Greek pledge, mill and slaves at 12%
Growth of a Herd of Cattle in Ten Years
In 1967, I. J. Gelb published “Growth of a Herd of Cattle in Ten Years” based on a Sumerian UrIII tablet circa 2000 BCE, < Drehem TCL II; Paris, 1911 No. 5499 >. The translation reports that a herd of 6 cattle grew to 32 cattle after 10 years. The analysis uses some TCL interest calculations on the cattle herd report. The normalized bounds on the cattle herd was 1 to 5.3333, from expr { 6./6}, 1. to expr { 32./6}, 5.3333. The TCL proc interest_continuous_compounding < 32. 6. 10> returned 0.1674 or 16.74 percent in interest. The TCL proc interest_continuous_compounding < 5.3333 1. 10 > returned 0.1674 or 16.74 percent. The converted Babylonian interest would expr { .16666 * 60.}, 9.9996, rounded and expressed as 10/60 Base_60. In terms of conventional Babylonian silver interest rates, the cattle growth rate of 10/60 compares to the usual silver interest rate of 12/60 or 1/5. The cattle Principal and Interest P&I would be 1+10/60, Base_60. In modern terms and probably numerical coincidence, loans of silver at 16.666 percent have been reported in Late Babylon and Ancient Greece, almost 1500 years later than the URIII tablet Drehem5499.
;# trial continuous_compounding < 32. 6. 10>
set cattle_herd_interest [expr { (100.* log ( (32.) /6. )) / (10. * log (exp(1.) ) ) }]
;# returns 16.74 percentThe cuneiform records used several forms for the multiplication operation in the interest rate problems. Not sure about the connotation of these multiplication terms, but the math texts use at least 4 different terms for multiplication, aside from the various languages. The terms ana (multiply addition) and ara (multiply area or multiply step) were used in interest rate problems. Multiplication by reciprocal is called "raising" and raise was used in the interest rate problems. The term ib_si was used to raise number to a power, but was also used in tables of squares and cubes. Although the use of ib_si for exponents was rare in the extant problems and tables, the cuneiform term ib_si is a math operation like a two way street, either raising a number to a power or effectively taking the logarithm. For example, 4 2 ib_si 16 or 16 (30/60) ib_si 4. The term sutakiilum (Lkti/l.kti.kti) (multiply holding or multiply slant) was also present. The hand tablets used in the schools were Sumerian IM.SU (literally mud in hand) or Akkadian imsukkum, ref Fowler and Robson. Imsukkum also means chamber pot in Akkadian. The term an has been handed down as Anna , Ann, or Dana, personal name and Celtic goddess of plenty. The term area in English is derived from the term "ara", Sumerian for multiplication.The term ara was used on the multiplication tables, so maybe ara has connotation of table lookup? The term sutakkile means literally hold in hand. The connotation of sutakkile was saving a number either as counting token, memory or scrap tablet, as moderns might say, carry over a number or remember for next calculation.
Table 4. Reconstructed listing of Babylonian Base_60 inverse reciprocals, ref interest rates
gold 6/6/2021. updated table on inverse reciprocals
| Table 4 for Base_60 inverse reciprocals | printed in | tcl wiki format | ||
|---|---|---|---|---|
| Base_60 value | Base_60 inverse reciprocals or 60 / value | Base_10 value | Base_10 value of Base_60 inverse reciprocals | comment, if any |
| tablet value | base_60 reciprocal | |||
| 2 | 30 | 2 | 30 | |
| 3 | 20 | 3 | 20 | |
| 4 | 15 | 4 | 15 | |
| 5 | 12 | 5 | 12 | |
| 6 | 10 | 6 | 10 | |
| 8 | 7 30 | 8 | 7.5 | |
| 9 | 6 40 | 9 | 6.6666 | |
| 10 | 6 | 10 | 6 | |
| 12 | 5 | 12 | 5 | |
| 15 | 4 | 15 | 4 | |
| 16 | 3 45 | 16 | 3.75 | tablets for first ten powers of 3:45, interest rates??? |
| 18 | 3 20 | 18 | 3.3333 | |
| 20 | 3 | 20 | 3 | |
| 24 | 2 30 | 24 | 2.5 | |
| 25 | 2 24 | 25 | 2.4 | |
| 27 | 2 13 20 | 27 | 2.2222 | |
| 30 | 2 | 30 | 2 | |
| 32 | 1 52 30 | 32 | 1.875 | |
| 36 | 1 40 | 36 | 1.6666 | tablets for first ten powers of 1:40, interest rates??? |
| 40 | 1 30 | 40 | 1.5 | |
| 45 | 1 20 | 45 | 1.3333 | possible dealing with grain interest rate of 33 percent??? |
| 48 | 1 15 | 48 | 1.25 | |
| 50 | 1 12 | 50 | 1.2 | possible dealing with silver interest rate??? |
| 54 | 1 06 40 | 54 | 1.1111 | |
| 1 | 1 | 1 | 1 | exception handling alert 1=1 NE ( 60/value ) |
| 1 04 | 56 15 | 1.06666 | 56.250 | |
| 1 12 | 50 | 1.2 | 50 | superfluous, often omitted, possible dealing with silver interest rate of 20 percent??? |
| 1 15 | 48 | 1.25 | 48 | superfluous, often omitted, possible dealing with L.B. silver interest rate of 25 percent??? |
| 1 20 | 45 | 1.33333 | 45.000 | superfluous, often omitted, possible dealing with grain interest rate 33 percent??? |
| 1 21 | 44 26 40 | 1.35 | 44.4444 | speculative, possible dealing with silver interest rate 35 percent??? |
| Note: | Babylonian mathematicians did >> not! << | usually use zeros | but in few instances | |
| Note: | Babylonian mathematicians separated Base_60 powers by spaces or gaps. | Moderns sometimes use periods (.) |
Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program.
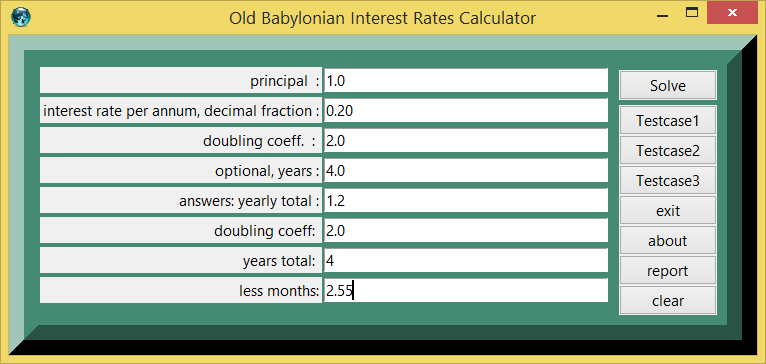
Testcase 1
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 1 | |
| 1.0 : | principal | |
| 0.20 : | interest rate decimal fraction | |
| 2.0 : | doubling coefficient | |
| 4.0 : | optional putative number of years | |
| 1.2 : | annual principal times interest rate | |
| 2.0 : | doubling coefficient | |
| 4 : | years of 360 days | |
| 2.55 : | less months of 30 days | |
| 3.787: | years from 4-(2.555/12.) |
Testcase 2
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 2 | |
| 1.0 : | principal | |
| 0.333 : | interest rate decimal fraction | |
| 2.0 : | doubling coefficient | |
| 3.0 : | optional putative number of years | |
| 1.333 : | answers: annual principal plus interest amount | |
| 2.0 : | doubling coefficient | |
| 3 : | years of 360 days | |
| 7.47 : | less months of 30 days | |
| 2.3775 : | years from 3-(7.47/12.) |
Testcase 33
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 3 | |
| 1.0 : | principal | |
| 0.5 : | interest rate decimal fraction | |
| 2.0 : | doubling coefficient | |
| 2.0 : | optional putative number of years | |
| 1.5 : | answers: annual principal plus interest amount | |
| 2.0 : | doubling coefficient | |
| 2 : | years of 360 days | |
| 4. : | less months of 30 days | |
| 1.66: | years from 2-(4./12.) |
Screenshots Section
figure 1.
figure 2.
figure 3.
figure 4.Solution for small fry, silver loans from 1 to 10 years
figure 5.Silver loans detail
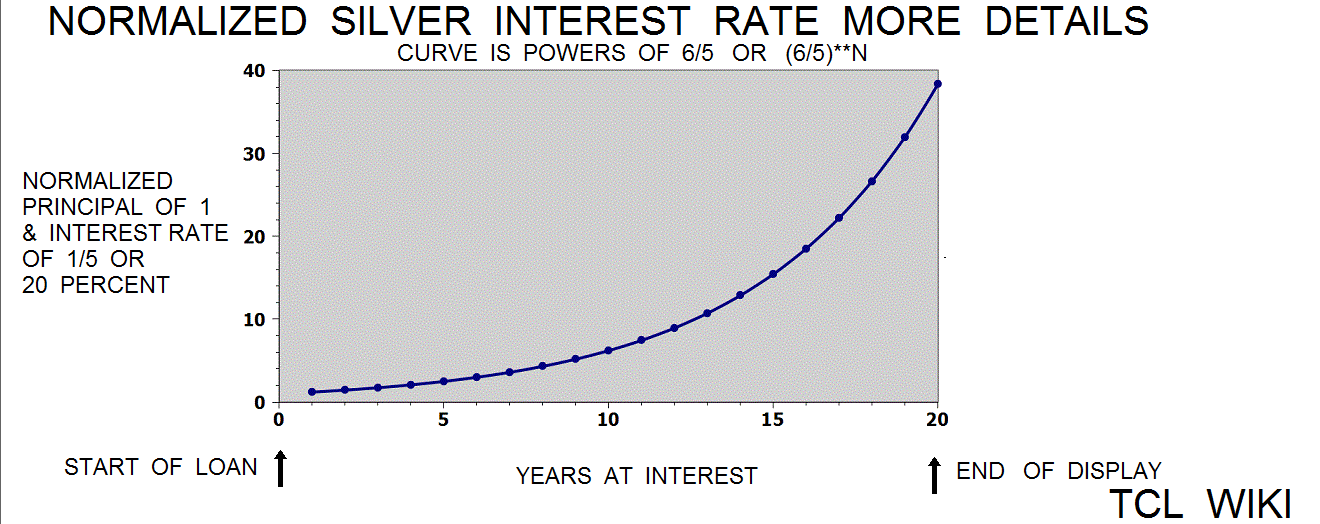
figure 6.Linear piece fit of year(N)*(6/5)*(1/2) to Silver loan curve (6/5)**N
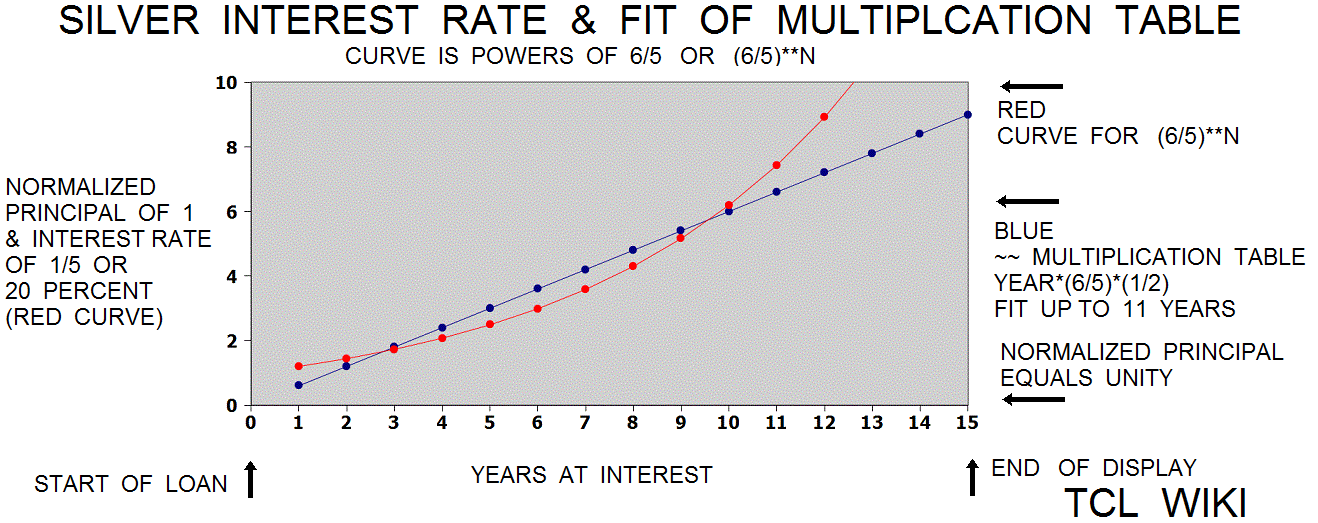
figure 7. Silver loans high scale
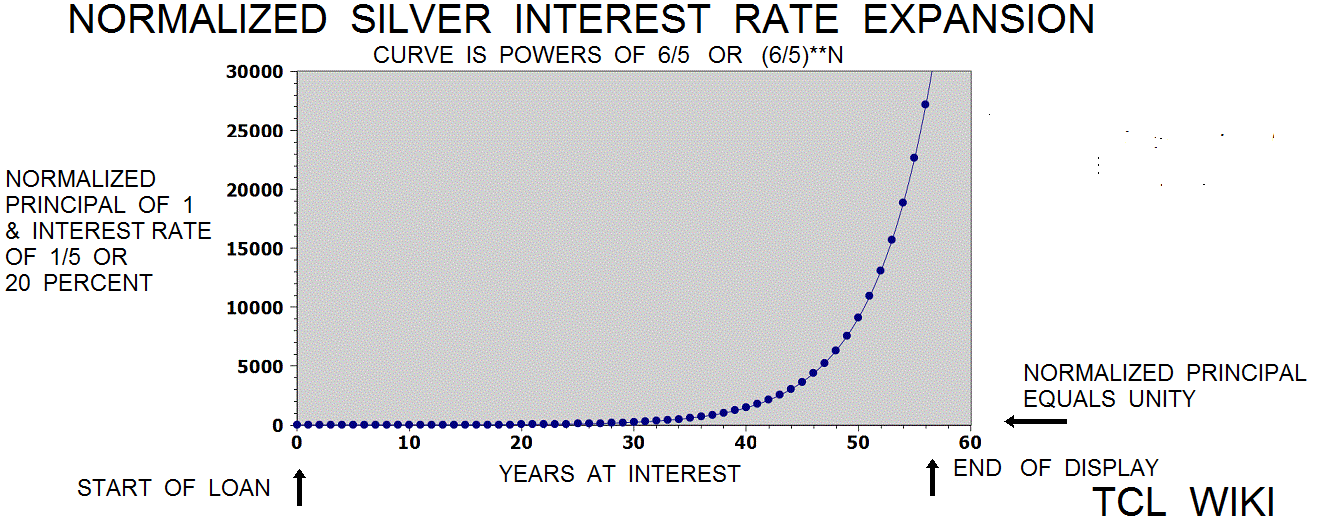
figure 8. Graphical Solution for Problem
figure 9. Graphical Solution Extra Chart
figure 10. Graphical Solution for Grain
References:
- Wikipedia search engine < doubling time >
- Wikipedia search engine < compound interest >
- Wikipedia search engine < Interest Rates >
- Google search engine < compound interest >
- Book >> Mathematical Cuneiform Texts, Otto Neugebauer and Abraham Sachs
- One Liners Programs Pie in the Sky
- One Liners
- One Liners Programs Compendium [L1 ]
- en.wikipedia.org/wiki/Doubling_time
- google < Babylonian Interest Rates Wikipedia >
- Ancient Babylonian Algorithms, Donald E. Knuth, Stanford University
- The oldest example of compound interest in Sumer, seventh power of four thirds (4/3)**7 , Kazuo MUROI
- Interest, Price, and Profit: An Overview of Mathematical Economics in YBC 46981,
- Robert Middeke-Conlin Christine Proust, CNRS and Université Paris Diderot
- Compound Interest Doubling Time Rule: Extensions and Examples from Antiquities,
- Saad Taha Bakir, ISSN: 2241 - 1968 (print), 2241 – 195X (online)
- Two Sumerian Words of Fractions in Babylonian Mathematics: igi-n-gál and igi-te-en , Kazuo MUROI
- O. Neugebauer and A. Sachs, Mathematical Cuneiform Texts, American Oriental Society, Series 29. New Haven, 1945.
- K. Muroi, Interest Calculation in Babylonian Mathematics:
- New Interpretations of VAT 8521 and VAT 8528, Historia Scientiarum, 39, (1990), 29-34
- O. Nuegebauer, The Exact Sciences in Antiquity, Second edition, Dover Publication Inc., New York, 1969
- Robert Middeke-Conlin & Christine Proust,Cuneiform Digital Library Journal 2014:3
- Interest, Price, and Profit: An Overview of Mathematical Economics in YBC 46981,
- The old Babylonian loan contract: its history and geography, Aaron Jacob Skaist,
- Bar-Ilan University Press, 1994
- Why the "Miracle of Compound Interest" leads to Financial Crises, by Michael Hudson
- Have we caught your interest?, by John H. Webb
- Exponential growth, doubling time, and the Rule of 70
- Colorado Alliance for Immigration Reform
- Montelle C. (2009) MLC 2078 and the History of the Mathematical Table.
- Adelaide, Australia: Australian Mathematical Society, 1 Sep 2009 (Conference)
- The powers of 9 and related mathematical tables from Babylon,
- Mathieu Ossendrijver (Humboldt University, Berlin)
- Mesopotamia, interest rate problem, Rosa Jiménez Iraundegui , Spanish Ministry of Education. Year 2001
- btcm.co/ancient-greek-interest-rates/
Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# Old Babylonian Interest Rates calculator
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI, 15dec2016
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {principal :} }
lappend names {interest rate per annum, decimal fraction :}
lappend names {doubling coeff. : }
lappend names {optional, years :}
lappend names {answers: principal plus interest :}
lappend names {doubling coeff: }
lappend names {years total: }
lappend names {less months:}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Old Babylonian Interest Rates
from TCL WIKI,
written on eTCL "
tk_messageBox -title "About" -message $msg }
proc double_function { principle doubling_coeff } {
set term_years 0
set counter 0
while { $counter < 50. } {
set term_years $counter
if { [** $principle $term_years ] > $doubling_coeff } {break}
incr counter
}
return $term_years }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global modern_formula_lump
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set principal $side1
set interest $side2
set optional_years $side4
set doubling_coeff $side3
set n [+ $principal [* $principal $interest ] ]
set rate .2
set solve_years [double_function $n $doubling_coeff ]
set solve_years_minus1 [- $solve_years 1 ]
#set months [expr 12*((1+$rate)**($n-2))/((1+$rate)**$n-(1+$rate)**($n-1))]
#set months [* 12. [/ [- [** $n 4. ] 2. ] [- [** $n 4. ] [** $n 3. ] ] ]]
set months [* 12. [/ [- [** $n $solve_years ] 2. ] [- [** $n $solve_years ] [** $n $solve_years_minus1 ] ] ]]
set modern_formula_lump [* $principal [** [+ 1. $interest] $optional_years ] ]
set side5 $n
set side6 $doubling_coeff
set side7 $solve_years
set side8 $months
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global switch_factor
global modern_formula_lump
global testcase_number
console show;
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| testcase number:|$testcase_number | |&"
puts "&| $side1 :|principal| |&"
puts "&| $side2 :|interest rate decimal fraction | |& "
puts "&| $side3 :|doubling coefficient | |& "
puts "&| $side4 :|optional number of years for lump sum| |&"
puts "&| $modern_formula_lump :|modern formula lump sum| |&"
puts "&| $side5 :|answers: annual principal plus interest amount | |&"
puts "&| $side6 :|doubling coefficient | |&"
puts "&| $side7 :|years of 360 days | |&"
puts "&| $side8 :|less months of 30 days | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 1.0 0.2 2.0 4.0 1.22 2.0 2.50 2.5}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 1.0 0.333 2.0 3.0 1.33 2.0 3.00 7.5 }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 1.0 0.5 2.0 2.0 1.33 2.0 2.00 4.0 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Old Babylonian Interest Rates Calculator" Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
Console Program for Sumerian interest concept, modern notation
# pretty print from autoindent and ased editor
# trial Sumerian interest concept, modern notation
# working under TCL version 8.5.6 and eTCL 1.0.1
# console program written on Windows XP on eTCL
# gold on TCL WIKI, 2Mar2017
package require Tk
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
console show
proc ::tcl::mathfunc::precision {precision float} {
# tcl:wiki:Floating-point formatting, [AM]
set x [ expr {round( 10 ** $precision * $float) / (10.0 ** $precision)} ]
# rounded or clipped to nearest 5ird significant figure
set x [ format "%#.5g" $x ]
return $x
}
puts "%|table for trial Sumerian interest concept, modern notation |||printed in| tcl wiki format|% "
puts "&| nth year | mixed p&i w/ base60 fraction |decimal p&i rounded 5th significant |decimal carried significant figures | comment, if any|& "
set counter 1
set i 2000
set ticker 1
while {$i>0} {
if { $ticker > 20 } { break }
set trial [ expr { rand() } ]
set yearly_amount [expr { (4./3.)**$counter } ]
set yearly_rnd_amount [::tcl::mathfunc::precision 5 $yearly_amount ]
set sixty_fraction [round [* 60. [- $yearly_rnd_amount [int $yearly_rnd_amount ]]]]
set sixty_fractionx [int $yearly_rnd_amount ]
puts "&| $ticker year :|$sixty_fractionx ; $sixty_fraction| $yearly_rnd_amount| $yearly_amount | |& "
incr counter
incr ticker
incr i -1
}
#end of fileTable for Sumerian interest concept (4/3), modern notation of 33 percent per year
| table for trial Sumerian interest concept, modern notation | p&i = (4/3)**N | p&i = (4/3)**N | printed in tcl wiki format | |
|---|---|---|---|---|
| nth year | mixed p&i w/ base60 fraction | decimal p&i rounded 5th significant | decimal p&i carried significant figures | comment, if any |
| 1 year : | 1 ; 20 | 1.3333 | 1.3333333333333333 | principal=1, return = 1+ (1/3) |
| 2 year : | 1 ; 47 | 1.7778 | 1.7777777777777777 | |
| 3 year : | 2 ; 22 | 2.3704 | 2.3703703703703698 | return doubles between year 2 and year 3 |
| 4 year : | 3 ; 10 | 3.1605 | 3.1604938271604932 | |
| 5 year : | 4 ; 13 | 4.2140 | 4.2139917695473237 | |
| 6 year : | 5 ; 37 | 5.6187 | 5.6186556927297646 | |
| 7 year : | 7 ; 30 | 7.4915 | 7.4915409236396862 | Muroi solution at 7 years |
| 8 year : | 9 ; 59 | 9.9887 | 9.9887212315195804 | |
| 9 year : | 13 ; 19 | 13.318 | 13.318294975359441 | |
| 10 year : | 17 ; 45 | 17.758 | 17.757726633812588 | |
| 11 year : | 23 ; 41 | 23.677 | 23.676968845083447 | |
| 12 year : | 31 ; 34 | 31.569 | 31.569291793444595 | |
| 13 year : | 42 ; 6 | 42.092 | 42.092389057926127 | |
| 14 year : | 56 ; 7 | 56.123 | 56.123185410568162 | |
| 15 year : | 74 ; 50 | 74.831 | 74.830913880757549 | |
| 16 year : | 99 ; 47 | 99.775 | 99.774551841010052 | |
| 17 year : | 133 ; 2 | 133.03 | 133.03273578801341 | |
| 18 year : | 177 ; 23 | 177.38 | 177.37698105068452 | |
| 19 year : | 236 ; 30 | 236.50 | 236.50264140091269 | |
| 20 year : | 315 ; 20 | 315.34 | 315.33685520121691 |
Table for Sumerian interest concept (6/5), modern notation of 20 percent per year
| table for trial Sumerian interest concept (6/5), modern notation | p&i = (6/5)**N | p&i = (6/5)**N | printed in tcl wiki format | |
|---|---|---|---|---|
| nth year | mixed p&i w/ base60 fraction | decimal p&i rounded 5th significant | decimal carried significant figures | comment, if any |
| 1 year : | 1 ; 12 | 1.2000 | 1.2 | principal=1, return = 1+(1/5) |
| 2 year : | 1 ; 26 | 1.4400 | 1.4399999999999999 | |
| 3 year : | 1 ; 44 | 1.7280 | 1.7279999999999998 | |
| 4 year : | 2 ; 4 | 2.0736 | 2.0735999999999999 | return doubles between year 3 and year 4 |
| 5 year : | 2 ; 29 | 2.4883 | 2.4883199999999994 | |
| 6 year : | 2 ; 59 | 2.9860 | 2.9859839999999993 | |
| 7 year : | 3 ; 35 | 3.5832 | 3.5831807999999992 | |
| 8 year : | 4 ; 18 | 4.2998 | 4.2998169599999985 | |
| 9 year : | 5 ; 10 | 5.1598 | 5.1597803519999985 | |
| 10 year : | 6 ; 12 | 6.1917 | 6.1917364223999973 | |
| 11 year : | 7 ; 26 | 7.4301 | 7.430083706879997 | |
| 12 year : | 8 ; 55 | 8.9161 | 8.916100448255996 | |
| 13 year : | 10 ; 42 | 10.699 | 10.699320537907195 | |
| 14 year : | 12 ; 50 | 12.839 | 12.839184645488633 | |
| 15 year : | 15 ; 24 | 15.407 | 15.407021574586359 | |
| 16 year : | 18 ; 29 | 18.488 | 18.488425889503631 | |
| 17 year : | 22 ; 11 | 22.186 | 22.186111067404354 | |
| 18 year : | 26 ; 37 | 26.623 | 26.623333280885227 | |
| 19 year : | 31 ; 57 | 31.948 | 31.947999937062271 | |
| 20 year : | 38 ; 20 | 38.338 | 38.337599924474723 |
test. 70/20 as 3.5 years , 70/(1/5)= 70(100/5)=3.5x
Open Office Spreadsheets for Compound Interest Rates for Silver and Grain
| Table of Compound Interest for Silver | Silver Problem Normalized to 1 | from Open_Office Spreadsheet | decimal & modern notation | (1+1/5) equivalent 20% per annum | |||
|---|---|---|---|---|---|---|---|
| Year | End Balance | Cumulative Invested | Cumulative Interest | Rate | Estimated Annual Interest | comment | |
| 1.000000 | initial dough, principal | ||||||
| 1 | 1.200010 | 1 | 0.200000 | 20.00% | 0.200000 | equivalent rate is 1/5 | |
| 2 | 1.440022 | 1 | 0.440002 | 20.00% | 0.240002 | ||
| 3 | 1.728036 | 1 | 0.728006 | 20.00% | 0.288004 | B. solution boundary point | |
| 4 | 2.073654 | 1 | 1.073614 | 20.00% | 0.345607 | B. solution boundary point | |
| 5 | 2.488394 | 1 | 1.488344 | 20.00% | 0.414731 | rule of thumb point | |
| 6 | 2.986083 | 1 | 1.986023 | 20.00% | 0.497679 | ||
| 7 | 3.583310 | 1 | 2.583240 | 20.00% | 0.597217 | ||
| 8 | 4.299982 | 1 | 3.299902 | 20.00% | 0.716662 | ||
| 9 | 5.159988 | 1 | 4.159898 | 20.00% | 0.859996 | ~4X | |
| 10 | 6.191996 | 1 | 5.191896 | 20.00% | 1.031998 | ||
| 11 | 7.430405 | 1 | 6.430295 | 20.00% | 1.238399 | ||
| 12 | 8.916496 | 1 | 7.916376 | 20.00% | 1.486081 | ~8X | |
| 13 | 10.699806 | 1 | 9.699676 | 20.00% | 1.783299 | ||
| 14 | 12.839777 | 1 | 11.839637 | 20.00% | 2.139961 | ||
| 15 | 15.407742 | 1 | 14.407592 | 20.00% | 2.567955 | ||
| 16 | 18.489300 | 1 | 17.489140 | 20.00% | 3.081548 | >16X | |
| 17 | 22.187170 | 1 | 21.187000 | 20.00% | 3.697860 | ||
| 18 | 26.624614 | 1 | 25.624434 | 20.00% | 4.437434 | ||
| 19 | 31.949547 | 1 | 30.949357 | 20.00% | 5.324923 | ||
| 20 | 38.339467 | 1 | 37.339267 | 20.00% | 6.389909 | ||
| 21 | 46.007370 | 1 | 45.007160 | 20.00% | 7.667893 | ||
| 22 | 55.208854 | 1 | 54.208634 | 20.00% | 9.201474 | ||
| 23 | 66.250635 | 1 | 65.250405 | 20.00% | 11.041771 | ||
| 24 | 79.500772 | 1 | 78.500532 | 20.00% | 13.250127 | ||
| 25 | 95.400936 | 1 | 94.400686 | 20.00% | 15.900154 |
| Table of Compound Interest for Grain | Muroi Solution Normalized to 1 | from Open_Office Spreadsheet | decimal & modern notation | (1+1/3) equivalent 33.33% per annum | ||
|---|---|---|---|---|---|---|
| Year | End Balance | Cumulative Invested | Cumulative Interest | Rate | Estimated Annual Interest | |
| 0 | 1.0000000 | initial dough, principal normalized to 1 | ||||
| 1 | 1.3333433 | 1 | 0.3333333 | 33.33% | 0.3333333 | equivalent rate is 1/3 |
| 2 | 1.7778011 | 1 | 0.7777811 | 33.33% | 0.4444478 | rule of thumb points |
| 3 | 2.3704115 | 1 | 1.3703815 | 33.33% | 0.5926004 | rule of thumb points |
| 4 | 3.1605586 | 1 | 2.1605186 | 33.33% | 0.7901372 | ~2X |
| 5 | 4.2140882 | 1 | 3.2140382 | 33.33% | 1.0535195 | |
| 6 | 5.6187942 | 1 | 4.6187342 | 33.33% | 1.4046961 | >4X |
| 7 | 7.4917357 | 1 | 6.4916657 | 33.33% | 1.8729314 | Muroi solution for compound interest problem |
| 8 | 9.9889909 | 1 | 8.9889109 | 33.33% | 2.4972452 | ~10X |
| 9 | 13.3186645 | 1 | 12.3185745 | 33.33% | 3.3296636 | |
| 10 | 17.7582293 | 1 | 16.7581293 | 33.33% | 4.4395548 | |
| 11 | 23.6776491 | 1 | 22.6775391 | 33.33% | 5.9194098 | |
| 12 | 31.5702088 | 1 | 30.5700888 | 33.33% | 7.8925497 | ~32X |
| 13 | 42.0936217 | 1 | 41.0934917 | 33.33% | 10.5234029 | |
| 14 | 56.1248389 | 1 | 55.1246989 | 33.33% | 14.0312072 | >50X |
| 15 | 74.8331285 | 1 | 73.8329785 | 33.33% | 18.7082796 | |
| 16 | 99.7775147 | 1 | 98.7773547 | 33.33% | 24.9443762 | |
| 17 | 133.0366962 | 1 | 132.0365262 | 33.33% | 33.2591715 | |
| 18 | 177.3822716 | 1 | 176.3820916 | 33.33% | 44.3455654 | |
| 19 | 236.5097054 | 1 | 235.5095154 | 33.33% | 59.1274238 | |
| 20 | 315.3462837 | 1 | 314.3460837 | 33.33% | 78.8365684 | |
| 21 | 420.4617215 | 1 | 419.4615115 | 33.33% | 105.1154278 | |
| 22 | 560.6156386 | 1 | 559.6154186 | 33.33% | 140.1539070 | >500X |
| 23 | 747.4875279 | 1 | 746.4872979 | 33.33% | 186.8718793 | |
| 24 | 996.6500470 | 1 | 995.6498070 | 33.33% | 249.1625091 | ~1000X |
| 25 | 1328.866739 | 1 | 1327.866489 | 33.33% | 332.2166820 |
Normalized Simple Interest Table at 20 percent
| Normalized Simple Interest Table at 20 percent per year | Open Office ods printed in TCL format | ||||||
| Year | Estimated Annual Interest | Year | End Balance | Cumulative Invested | Cumulative Interest | Interest Rate percent | comments if any |
| 1.000000 | initial dough, principal, normalized to one | ||||||
| 1 | 0.200000 | 1 | 1.200010 | 1.00 | 0.200000 | 20.00% | Ur-Nanna law |
| 2 | 0.200000 | 2 | 1.400020 | 1.00 | 0.400000 | 20.00% | all simple interest calculations |
| 3 | 0.200000 | 3 | 1.600030 | 1.00 | 0.600000 | 20.00% | |
| 4 | 0.200000 | 4 | 1.800040 | 1.00 | 0.800000 | 20.00% | |
| 5 | 0.200000 | 5 | 2.000050 | 1.00 | 1.000000 | 20.00% | B. rule of thimb |
| 6 | 0.200000 | 6 | 2.200060 | 1.00 | 1.200000 | 20.00% | |
| 7 | 0.200000 | 7 | 2.400070 | 1.00 | 1.400000 | 20.00% | |
| 8 | 0.200000 | 8 | 2.600080 | 1.00 | 1.600000 | 20.00% | |
| 9 | 0.200000 | 9 | 2.800090 | 1.00 | 1.800000 | 20.00% | |
| 10 | 0.200000 | 10 | 3.000100 | 1.00 | 2.000000 | 20.00% | |
| 11 | 0.200000 | 11 | 3.200110 | 1.00 | 2.200000 | 20.00% | |
| 12 | 0.200000 | 12 | 3.400120 | 1.00 | 2.400000 | 20.00% | |
| 13 | 0.200000 | 13 | 3.600130 | 1.00 | 2.600000 | 20.00% | |
| 14 | 0.200000 | 14 | 3.800140 | 1.00 | 2.800000 | 20.00% | |
| 15 | 0.200000 | 15 | 4.000150 | 1.00 | 3.000000 | 20.00% | |
| 16 | 0.200000 | 16 | 4.200160 | 1.00 | 3.200000 | 20.00% | |
| 17 | 0.200000 | 17 | 4.400170 | 1.00 | 3.400000 | 20.00% | |
| 18 | 0.200000 | 18 | 4.600180 | 1.00 | 3.600000 | 20.00% | |
| 19 | 0.200000 | 19 | 4.800190 | 1.00 | 3.800000 | 20.00% | |
| 20 | 0.200000 | 20 | 5.000200 | 1.00 | 4.000000 | 20.00% | |
| 21 | 0.200000 | 21 | 5.200210 | 1.00 | 4.200000 | 20.00% | |
| 22 | 0.200000 | 22 | 5.400220 | 1.00 | 4.400000 | 20.00% | |
| 23 | 0.200000 | 23 | 5.600230 | 1.00 | 4.600000 | 20.00% | |
| 24 | 0.200000 | 24 | 5.800240 | 1.00 | 4.800000 | 20.00% | |
| 25 | 0.200000 | 25 | 6.000250 | 1.00 | 5.000000 | 20.00% |
Normalized Simple Interest Table at 33.33 percent
| Normalized Simple Interest Table at 33.33 percent per year | Open Office ods printed in TCL format | ||||||
|---|---|---|---|---|---|---|---|
| Year | Estimated Annual Interest | Year | End Balance | Cumulative Invested | Cumulative Interest | Interset Rate percent | comments if any |
| 1.000000 | initial dough, principal normalized to one | ||||||
| 1 | 0.333333 | 1 | 1.333310 | 1.00 | 0.333300 | 33.33% | Ur-Nanna Law |
| 2 | 0.333333 | 2 | 1.666653 | 1.00 | 0.666633 | 33.33% | B. rule of thumb??? |
| 3 | 0.333333 | 3 | 1.999997 | 1.00 | 0.999967 | 33.33% | |
| 4 | 0.333333 | 4 | 2.333340 | 1.00 | 1.333300 | 33.33% | |
| 5 | 0.333333 | 5 | 2.666683 | 1.00 | 1.666633 | 33.33% | |
| 6 | 0.333333 | 6 | 3.000027 | 1.00 | 1.999967 | 33.33% | |
| 7 | 0.333333 | 7 | 3.333370 | 1.00 | 2.333300 | 33.33% | |
| 8 | 0.333333 | 8 | 3.666713 | 1.00 | 2.666633 | 33.33% | |
| 9 | 0.333333 | 9 | 4.000056 | 1.00 | 2.999966 | 33.33% | |
| 10 | 0.333333 | 10 | 4.333400 | 1.00 | 3.333300 | 33.33% | |
| 11 | 0.333333 | 11 | 4.666743 | 1.00 | 3.666633 | 33.33% | |
| 12 | 0.333333 | 12 | 5.000086 | 1.00 | 3.999966 | 33.33% | |
| 13 | 0.333333 | 13 | 5.333430 | 1.00 | 4.333300 | 33.33% | |
| 14 | 0.333333 | 14 | 5.666773 | 1.00 | 4.666633 | 33.33% | |
| 15 | 0.333333 | 15 | 6.000116 | 1.00 | 4.999966 | 33.33% | |
| 16 | 0.333333 | 16 | 6.333460 | 1.00 | 5.333300 | 33.33% | |
| 17 | 0.333333 | 17 | 6.666803 | 1.00 | 5.666633 | 33.33% | |
| 18 | 0.333333 | 18 | 7.000146 | 1.00 | 5.999966 | 33.33% | |
| 19 | 0.333333 | 19 | 7.333489 | 1.00 | 6.333299 | 33.33% | |
| 20 | 0.333333 | 20 | 7.666833 | 1.00 | 6.666633 | 33.33% | |
| 21 | 0.333333 | 21 | 8.000176 | 1.00 | 6.999966 | 33.33% | |
| 22 | 0.333333 | 22 | 8.333519 | 1.00 | 7.333299 | 33.33% | |
| 23 | 0.333333 | 23 | 8.666863 | 1.00 | 7.666633 | 33.33% | |
| 24 | 0.333333 | 24 | 9.000206 | 1.00 | 7.999966 | 33.33% | |
| 25 | 0.333333 | 25 | 9.333549 | 1.00 | 8.333299 | 33.33% |
One Liners Programs for Interest Rates, updated
gold 6/7/2021. Updated from One Liners Programs Compendium, [L2 ]
;# These statements should be pastable into the easy eye console.
;# Alternate and redundant calculations for comparison with
;# approximation results ref. different internet articles and tablets.
;# The Babylonians did not use either algebra, modern equations notation, or interest rates in percent.
;# Babylonians used interest rates expressed in Base_60 rational fractions and Base_60 inverse reciprocals.
;# ***** simple interest problems in TCL one liners procedures *****
;# find simple interest amount from 3 entries as < principal interest years >
proc simple_interest_amount { principal interest years } { expr { ($principal*1.)*(1.+$years*$interest )}}
;# Usage simple_interest_amount 5000. .05 7. returns 6750.0
;# find simple interest principal from 3 entries as < amount interest years >
proc simple_interest_principal { amount interest years } { expr { ($amount*1.)/(1.+$years*$interest )}}
;# Usage simple_interest_principal 6750.0 .05 7. returns 5000.0
;# find simple interest rate from 3 entries as < amount principal years >
proc simple_interest_rate { amount principal years } { expr { ((($amount*1.)/$principal)-1.)/$years }}
;# Usage simple_interest_rate 6750.0 5000. 7. returns 0.05
;# find years of simple interest from 3 entries as < amount principal interest >
proc simple_interest_years { amount principal interest } { expr { ((($amount*1.)/$principal)-1.)/$interest }}
;# Usage simple_interest_years 6750.0 5000. .05 returns 7.0
;# ****** compound interest problems in TCL one liners procedures ******
;# find compound interest amount from 4 entries as < principal interest years compounding_times_per_year >
;# cd is compounding times per year, usually 4 quarters or 12 months
proc compound_interest_amount { principal interest years cd } { expr { ($principal*1.)*((1.+( $interest /$cd))**($years*$cd))}}
;# Usage compound_interest_amount 5000 .05 7 12 retuRns 7090.180
;# find compound interest principal from 4 entries as < amount interest years cd >
;# cd is compounding times per year, usually 4 quarters or 12 months
proc compound_interest_principal { amount interest years cd } { expr { $amount*( 1. +(($interest*1.)/$cd ) )**(-1.*$cd*$years)}}
;# Usage compound_interest_principal 7090.180 0.05 7 12 returns 4999.997, rounds to 5000.
;# find interest in compound interest from 4 entries as < amount principal years cd >
;# cd is compounding times per year, usually 4 quarters or 12 months
proc compound_interest_interest { amount principal years cd } { expr { $cd*((($amount*1.0)/$principal)**(1./($cd*$years))-1.)}}
;# Usage compound_interest_interest 7090.180 5000. 7 12 returns 0.049, rounds to 0.05
;# find years of compound interest from 4 entries as < amount principal interest cd>
proc compound_interest_years { amount principal interest cd } { expr { (log10 (($amount*1.0)/$principal)) / ($cd*log10(1.+(($interest*1.)/$cd) ) ) }}
;# Usage compound_interest_years 7090.180 5000. 0.05 12 returns 6.99, rounds to 7 years
;# ******** continuous_compounding ******* based on exponential formulas and natural log.
proc amount_continuous_compounding { principal interest years } { expr { $principal* exp ( $interest*$years*1. ) }}
;# Usage amount_continuous_compounding 5000. 0.05 7 returns 7095.3377
proc principal_continuous_compounding { amount interest years } { expr { $amount * exp ( $interest*$years* -1. ) }}
;# Usage principal_continuous_compounding 7095.33 0.05 7. returns 4999.994, rounds to 5000.
proc interest_continuous_compounding { amount principal years } { expr { (log ( ($amount*1.) /$principal )) / ($years * log (exp(1.) ) ) }}
;# Usage interest_continuous_compounding 7095.33 5000. 7 returns 0.04999, rounds to 0.05
proc years_continuous_compounding { amount principal interest } { expr { (log ( ($amount*1.) /$principal )) / ($interest * log (exp(1.) ) ) }}
;# Usage years_continuous_compounding 7095.33 5000. 0.05 returns 6.999, rounds to 7 years
proc eckart–mchale_69p3 {rate} { return [expr {(69.3/$rate) * (200./(200.-$rate))} ] }
;# 2nd order eckart–mchale, 20 percent interest rate doubles money in how many years?
;# eckart–mchale_69p3 20.0 ;# returns 3.85
;# 2nd order solution, should be not that far from exact 3.802?
proc pade_rule_69.3 { rate } { return [ (69.3/$rate) * (600.+4.* $rate)/(600.+$rate) ] }
;# pade_rule 20 percent interest rate doubles money in how many years?
;# Usage pade_rule_69p3 20.0 ;# returns 3.8
;# 3ird order solution, should be not that far from exact 3.802
;# following exact doubling rule etc in TCL using natural logarithms.
;# Denominator term < log (1.+ $rate/100.)> represents Principle and Interest P&I
;# Manipulating log term in nominator, log (2) for doubling,
;# and log (3) for tripling, log (1.5) for 50% (factor >.5<) rise.
;# extensions log (5) for 5X, log (10) for 10X, log (16) for 16X, etc.
proc exact_doubling_rule { rate } { return [ expr { log (2.) / log (1.+ $rate/100.)}] }
;# what is computation times (years here),
;# to double amount at interest rate of 20 percent
;# Usage <exact_doubling_rule 20. > returns 3.8017840169239308 years, rounds to 3.802
proc exact_tripling_rule { rate } { return [ expr { log (3.) / log (1.+ $rate/100.)}] }
;# what is computation times (years here),
;# to triple amount at interest rate of 20 percent
;# Usage <exact_tripling_rule 20 > ;# returns 6.0256 years
proc exact_rise_rule { rate } { return [ expr { log (1.5) / log (1.+ $rate/100.)}] }
;# what is computation times (years here),
;# to rise amount 50 percent (>.5< factor below)
;# at interest rate of 20 percent
;# Usage <exact_rise_rule 20. > ;# returns 2.2239 years
Comments Section
Please place any comments here with your wiki MONIKER and date, Thanks.
gold9dec2018. All, I have several vg's unable to load. says previous type was blank, new type is png . unable to change type.