Old_Babylonian_Interest_Rates_V2_and_TCL_demo_example_calculator_numerical_analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Its very hard to reply reasonably without some background of the correspondent on their Wiki bio page. Thanks,gold
Old_Babylonian_Interest_Rates and TCL demo example calculator
- Appendix Code
- Comments Section
Preface
gold Here are some calculations for Old_Babylonian_Interest_Rates using TCL expressions.
Introduction
In the cuneiform math problems and coefficient lists on clay tablets, there are coefficient numbers which were used in determining the amount of materials and the daily work rates of the workers. In most cases, the math problem is how the coefficient was used in estimating materials, work rates, and math problems. One difficulty is determining the effective magnitude or power of the number coefficient in the base60 notation. In cuneiform, numbers in base60 are written using a relative place notation. For example, 20 could represent either 20*3600,20,20/60, 20/3600, or even 1/20. The basic dimensions and final tallies were presented in the cuneiform accounts on clay tablets, but some calculations, some units, some explanations, and some problem answers (aw shucks!) were left off the tablet. The Babylonians did not use algebra notation, decimal notation, errors in percent, or modern units of measurement. So the reader will have to bear some anachronisms in the initial pseudocode preparations and final TCL code. At least one approach for the modern reader and using modern terminology is to develop the implied algebraic equations and decimal equivalents from the cuneiform numbers. Then the TCL calculator can be run over a number of testcases to validate the algebraic equations.
Common Interest Rates in Babylon
From the cuneiform clay tablets, the common interest rate for temple or institutional silver was 1/5 or 12/60 per year (360 days), and converted to decimal 0.2 or 20 percent for the calculator . The rule of thumb was for silver to double in 5 years. Another rule of thumb was that the silver interest per month was 1/60 as expr (1/60)*12 would give 12/60. The common interest rate including default debt obligations for barley or grain was 1/3 or 20/60 per year (360 days), and converted to decimal 0.333 or 33 percent for the calculator. The rule of thumb was for grain at 33.3 percent interest rate to double in 2 years. In some reigns, the harvest tax was 1/2 or 50 percent per annum and possibly listed as default debt interest on the books. In modern terms, the reported interest rates ranged from 20 to 50 percent per annum. In the Babylonian interest rate problems, a month is defined as thirty days and a year is defined as 360 days. However with base60 rounding and calculation slop, differences in results between the Babylonian year of 360 days and the modern year of 365 days are not usually discernable. The Babylonian method or "algorithm" was find the total years to double the annual sum of principal and interest, raising the exponent for years of the annual sum to approximate for double or other 2X multiple of the annual product, and interpolate the result for the years less months to double. Essentially from the available translated problems, the Babylonians are interpolating the solution between powers of 2. The Babylonians did not use interest rate in percent for their math problems, but it is worthwhile to compile some parallel results using either the modern rule of 70 or modern interest formulas. The modern rule of 70 for percent was doubling time equals expr { 70. / (100.*interest_rate_percent) }. Some modern texts refered to the alternate rule of 72 for easier fractions and rounding. The modern rule of 72 for percent was doubling time equals expr { 72. / (100.*interest_rate_percent)}. Another modern formula using natural logs was the doubling_time equals expr { ln 2 / rate_fraction } or multiples_time equals ln N1/ rate_fraction.
Specific Problem on Clay Tablet YBC-4669-rev
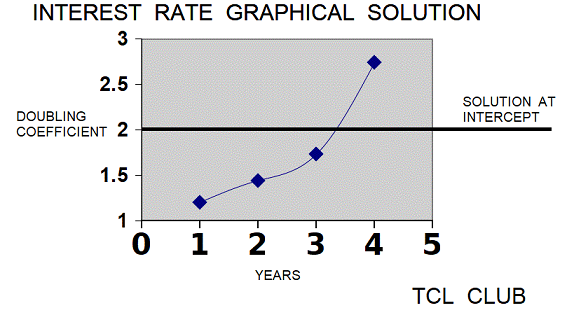
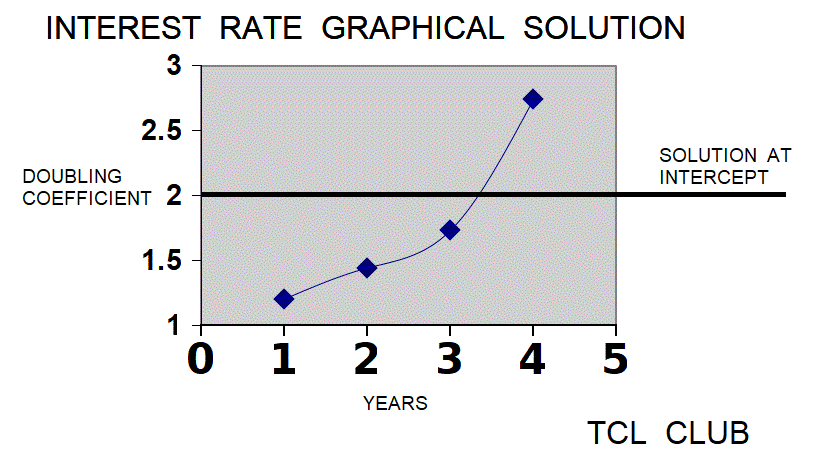
The clay tablet YBC-4669-rev was translated by Neugebauer and further discussed by Friberg and Al-Rawi. The interest amount is cited at one gur and the question is when or how many years will the principle equal the interest amount. If the interest amount = principal = one gur, then the P&I = 1+1 or 2 at the end of the last year. No method or answer result for the interest rate problem is given on the tablet, but a oneliner procedure was written in TCL. Since no interest rate is specified, presumably the interest rate is the silver rate at 20 percent interest. However, since the text specifies gur as a grain measure, there is a possibility that either the grain rate of 33 percent interest is meant or some other unknown rate to the modern reader. Although no answer is specified, it is desirable to establish boundaries on the problem using the rules of thumb, TCL code, and redundant methods. With trial and error method, the doubling formula equals expr (1+12./60.)*(1+12./60.)*(1+12./60.)*(1+12./60.) = 2.0736, where the answer is somewhat less than 4 years. Using the silver interest rate of 20 percent, an iterative solution is possible with procedure modern_formula_lump {1 .2 2} , succession modern_formula_lump{ 1 .2 3}, succession modern_formula_lump {1 .2 4}, where the approximate answer is 2.0736, roughly doubling in 4 years. An exact solution would be to interpolate between year 3 and year 4, as the TCL calculator does. As an alternate method, the TCL calculator with {1,.2,2} gives approximately 3 years, 9.5 months or 4 years rounding. Even considering the inadequate information, the problem in YBC-4669-rev is very similar to Testcase 1 already loaded in the TCL calculator.
Continuing with the clay tablet YBC-4669-rev as translated by Neugebauer. The interest rate problem is outlined in the text and the Babylonian answer is given as 34_43_20 base60. Asking for the silver principal, the givens are total Principal and Interest P&I was one shekel or one gin of silver. The term of loan was 3 years. In Babylonian terms, the interest payment were given as 1 mina per 12 shekels, the reciprocal of modern usage or expressions. In modern terms and inverted, the interest rate was 12 shekels over 60 shekels per year and would be expr { 12./60 }, 0.2 decimal, 20 percent. The Babylonians did not use percent, but the interest in percent is the most convenient form for the modern reader. The hand calculation in decimals is P&I = expr / 60. [* $principal [** [+ 1. $interest $year ]], expr { / 60. [* 1. [** [+ 1. .2 3. ]] }, 34.7222 decimal, converts to 34_43_20 base60. The term 60 is a units conversion. The numbers on the tablet are given in relative place value in base60 notation, so some problem boundaries are useful for checking absolute values of the base60 notation. The check on the boundaries of problem would be that the principal must be less than one shekel. The Babylonian rule of thumb is that silver doubles is two years. If 2*P equals 1 shekel in two years (reductio ad absurdam), then the answer for the interest problem for over three years must in range of a half shekel, 30/60 shekel. While the method was not on the tablet, the formula term (1+12/60)**year is a probable expression for the silver P&I and is considered a use for the Babylonian square and cube tables.
proc modern_formula_lump {principal interest year } {return [* $principal [** [+ 1. $interest] $year ]]}
modern_formula_lumpx {principal interest year } {return [/ 60. [* $principal [** [+ 1. $interest] $year ]]]}
# usage is modern_formula_lumpx 1. .2 3 # answer 34.7222 decimal , equivalent base_60 is 34_43_20
modern_formula_lump 1 .2 2 # answer 1.44
modern_formula_lump 1 .2 336 # answer 1.7279
modern_formula_lump 1 .2 4 # answer 2.0736 Testcases
The answer for the first testcase was between 3 years for 1.7279 factor and 4 years for 2.0736 factor, see above eTCL statements. The Babylonian solution interpolated between 3 and 4 years for the factor of 2, giving the answer in months short of 4 years. For comparison, the modern lump sum formula for 20 percent at 3.8 years gives factor 1.99. The second testcase was finding the doubling time at 33 percent interest rate. The answer for the second testcase was between 2 years for 1.7689 factor and 3 years for 2.3526 factor. The Babylonian method would interpolate between 2 and 3 years for the factor of 2, giving the answer in months short of 3 years. For comparison, the modern lump sum formula for 33 percent at 2.488 years gives factor 1.908 .The third testcase was finding the doubling time 50 percent interest rate. The answer for the third testcase was between 1 year for 1.5 factor and 2 years for 2.25 factor. The Babylonian method would interpolate between 1 and 2 years for the factor of 2, giving the answer in months short of 2 years. For comparison, the modern lump sum formula for 50 percent interest at 1.7 years gives factor 1.992 . Some testcases were developed to check the lump sum formula in the TCL calculator. For fifth testcase, the modern lump sum formula for principal of 1 and 12 percent interest at 7 years gives amount of 7.5 .For sixth testcase, the modern lump sum formula for principal of 1000 and 15 percent interest at 3 years gives amount of 1520. For seventh testcase, the modern lump sum formula for principal of 1000 and 33 percent interest at 5 years gives amount of 4208.
Conclusions
Table 1: Tables
Table 2: Tables
Testcases Section
Testcase 1
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 1 | |
| 1.0 : | principal | |
| 0.200 : | interest rate decimal fraction | |
| 2.0 : | doubling coefficient | |
| 4.0 : | optional number of years for lump sum | |
| 2.07359 : | modern formula lump sum | |
| 1.2 : | answers: annual principal plus interest amount | |
| 2.0 : | doubling coefficient | |
| 4 : | years of 360 days | |
| 2.5555 : | less months of 30 days |
Testcase 2
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 2 | |
| 1.0 : | principal | |
| 0.3330 : | interest rate decimal fraction | |
| 2.0 : | doubling coefficient | |
| 3.0 : | optional number of years for lump sum | |
| 2.36859 : | modern formula lump sum | |
| 1.333 : | answers: annual principal plus interest amount | |
| 2.0 : | doubling coefficient | |
| 3 : | years of 360 days | |
| 7.4752176213392945 : | less months of 30 days |
Testcase 3
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 1 | |
| 1.0 : | principal | |
| 0.5 : | interest rate decimal fraction | |
| 2.0 : | doubling coefficient | |
| 2.0 : | optional number of years for lump sum | |
| 2.25 : | modern formula lump sum | |
| 1.5 : | answers: annual principal plus interest amount | |
| 2.0 : | doubling coefficient | |
| 2 : | years of 360 days | |
| 4.0 : | less months of 30 days |
Screenshots Section
figure 1. Calculator Screenshot
figure 2. Console Screenshot
figure 3. Interpolation between Powers of 2
References:
- google < Babylonian Interest Rates >
- Wikipedia search engine < Doubling Time Rule >
- Wikipedia search engine < multiplication algorithm >
- Wikipedia search engine < Powers of 2 >
- Wikipedia search engine < compound interest >
- Wikipedia search engine < Sumer Babylonian mathematics >
- Wikipedia search engine <Donald E. Knuth >
- Wolfram Alpha search engine < Otto Neugebauer >
- Oneliner's Pie in the Sky
- One Liners
- google < Babylonian Interest Rates Wikipedia >
- Ancient Babylonian Algorithms, Donald E. Knuth, Stanford University
- The oldest example of compound interest in Sumer, seventh power of four thirds (4/3)**7 , Kazuo MUROI
- Interest, Price, and Prost: An Overview of Mathematical Economics in YBC 46981,
- Robert Middeke-Conlin, Christine Proust, CNRS and Université Paris Diderot
- Compound Interest Doubling Time Rule: Extensions and Examples from Antiquities,
- Saad Taha Bakir, ISSN: 2241 - 1968 (print), 2241 195X (online)
- Two Sumerian Words of Fractions in Babylonian Mathematics: igi-n-gál and igi-te-en , Kazuo MUROI
- O. Neugebauer and A. Sachs, Mathematical Cuneiform Texts, American Oriental Society, Series 29. New Haven, 1945.
- K. Muroi, Interest Calculation in Babylonian Mathematics:
- New Interpretations of VAT 8521 and VAT 8528, Historia Scientiarum, 39, (1990), 29-34
- O. Nuegebauer, The Exact Sciences in Antiquity, Second edition, Dover Publication Inc., New York, 1969
Pseudocode & Equations Section
# more than one formula for 1) tables and 2) calculator shell
# includes rule of 70 and rule of 72 in modern times, not ancient formulas
# following statements can be pasted into eTCL console
set rule_70_problem [/ 70. [* 100. .20 ]] # 3.5 years for doubling amount
set rule_70_problem [/ 70. [* 100. .333 ]] # 2.102 years for doubling amount
set rule_70_problem [/ 70. [* 100. .50 ]] # 1.4 years for doubling amount
set rule_70_problem [/ 70. [* 100. .05 ]] # 14.0 years for doubling amount
set ln_rule_problem [/ [log 2. ] [* 1. .2 ] ] # 3.4657 years for doubling amount
set ln_rule_problem [/ [log 4. ] [* 1. .2 ] ] # 6.931 years for 4X amount
set ln_rule_problem [/ [log 2. ] [* 1. .333 ] ] # 2.0815 years for doubling amount
set ln_rule_problem [/ [log 4. ] [* 1. .333 ] ] # 4.1630 years for 4X amount
set sum [+ 1. 0.2 ] # answer decimal 1.2
set months [* 12. [/ [- [** 1.2 4. ] 2. ] [- [** 1.2 4. ] [** 1.2 3. ] ] ]] # 2.555 less months of 30 days
set Babylon_problem [** 1.2 3. ] # answer decimal 1.7279
set babylon_problem2 [** 1.20 4. ] # answer decimal 2.0736
set sumer_problem [** [/ 4. 3. ] 7. ] # answer decimal 7.49154
Appendix Code
Trial GUI Shell
# TCL source code follows.
# pretty print from autoindent and ased editor
# Old Babylonian Interest Rates calculator V2
# written on Windows XP on eTCL
# working under TCL version 8.6
# gold on TCL club, 15nov2018
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {principal :} }
lappend names {interest rate per annum, decimal fraction :}
lappend names {doubling coeff. : }
lappend names {optional, years :}
lappend names {answers: principal plus interest :}
lappend names {doubling coeff: }
lappend names {years total: }
lappend names {less months:}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Old Babylonian Interest Rates
from TCL "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg "Calculator for Babylonian Interest Rates V2
from TCL ,
# self help listing
# B. interest problem is interpolating between exponents of 2,
# 4 givens follows.
1) principal
2) interest rate per annum
3) doubling coefficient, usually 2
4) optional, years
The Babylonians did not use modern algebraic notation,
percent, modern units, or modern terminolgy.
The interest rate solution from the clay tablets
is a genuine antique method from 1600 BCE
and different looking from modern math methods.
The TCL solution is adapted from the
clay tablets translated and explained by MCT etc.
For the modern reader and comparisons with modern formulas,
report may include percent, interest rate per annum,
and other modern terms.
In the Babylonian interest rate problems, a month is defined
as thirty days and a year is defined as 360 days.
However with base60 rounding and calculation slop,
differences in results between the Babylonian year
of 360 days and the modern year of 365 days are
not usually discernable.
# Cuneiform interest rate(s) derives from silver and trade in kind
# includes capacity in bushels of barley.
# However, there was lack of small currency and silver in
# Ancient Mesopotamia, especially among the common men
# Most transactions were in kind or figures on accounts.
# The common P&I rate for silver was (1+12/60), (1+1/5), or decimal 1.2
# The rule of thumb was for silver to double in 5 years.
# The common P&I rate for grain was (1+20/60), (1+1/3), or decimal 1.333
# The rule of thumb was for grain to double in 2 years.
# Grain and kind was also let at (1+12/60) or 20 percent in some problems.
# >>>> Copyright Notice <<<<<
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK 8.6 license terms.
# Editorial rights retained under the TCL/TK license terms
# and will be defended as necessary in court.
# >>>> Push Button Operation <<<<
# Recommended procedure is push testcase and fill frame,
# change first three entries etc, push solve,
# and then push report. Report allows copy and paste
# from console to conventional texteditor. For testcases,
# the testcase number is internal to the calculator and
# will not be printed until the report button is pushed
# for the current result numbers.
# Where the program defaults are recalled,
# canvas colors/features/variables/globals/calculations/clear displays
# are reset prior to calculation ( in push button list) .
# Buttons on the calculator are not limited to a single action procedure
# or single shot. A button command may call multiple statements and procs,
# effectively a separate program or subprogram installed as
# a list of procedures in a button. Alternately, the list of procedures
# need not be installed in a button, but the button
# may call a separate procedure.
Conventional text editor formulas or grabbed from internet
screens can be pasted into green console.
Try copy and paste following into green screen console
set answer [* 1. 2. 3. 4. 5. ]
returns 120
# gold on TCL Club, 15nov2018 "
tk_messageBox -title "About" -message $msg }
proc double_function { principle doubling_coeff } {
set term_years 0
set counter 0
while { $counter < 50. } {
set term_years $counter
if { [** $principle $term_years ] > $doubling_coeff } {break}
incr counter
}
return $term_years }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global modern_formula_lump
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set principal $side1
set interest $side2
set optional_years $side4
set doubling_coeff $side3
set n [+ $principal [* $principal $interest ] ]
set rate .2
set solve_years [double_function $n $doubling_coeff ]
set solve_years_minus1 [- $solve_years 1 ]
#set months [expr 12*((1+$rate)**($n-2))/((1+$rate)**$n-(1+$rate)**($n-1))]
#set months [* 12. [/ [- [** $n 4. ] 2. ] [- [** $n 4. ] [** $n 3. ] ] ]]
set months [* 12. [/ [- [** $n $solve_years ] 2. ] [- [** $n $solve_years ] [** $n $solve_years_minus1 ] ] ]]
set modern_formula_lump [* $principal [** [+ 1. $interest] $optional_years ] ]
set side5 $n
set side6 $doubling_coeff
set side7 $solve_years
set side8 $months
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global switch_factor
global modern_formula_lump
global testcase_number
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Babylonian Interest Rate Report , screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
console show;
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| testcase number:|$testcase_number | |&"
puts "&| $side1 :|principal| |&"
puts "&| $side2 :|interest rate decimal fraction | |& "
puts "&| $side3 :|doubling coefficient | |& "
puts "&| $side4 :|optional number of years for lump sum| |&"
puts "&| $modern_formula_lump :|modern formula lump sum| |&"
puts "&| $side5 :|answers: annual principal plus interest amount | |&"
puts "&| $side6 :|doubling coefficient | |&"
puts "&| $side7 :|years of 360 days | |&"
puts "&| $side8 :|less months of 30 days | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 1.0 0.2 2.0 4.0 1.22 2.0 2.50 2.5}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 1.0 0.333 2.0 3.0 1.33 2.0 3.00 7.5 }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 1.0 0.5 2.0 2.0 1.33 2.0 2.00 4.0 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .self_help -text self_help -command {self_help}
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Old Babylonian Interest Rates Calculator V2" gold This page is copyrighted under the TCL/TK license terms, this license .
Disclaimers: This page, screenshots, and TCL source code is copyrighted under the TCL/TK license terms. Editorial rights and disclaimers retained under the TCL/TK license terms and will be defended as necessary in court.
Comments Section
Please place any comments here, Thanks.