Polyhedron Nets
Keith Vetter 2003-03-06 - if you take a 3D solid shape--a polyhedron--and cut along certain edges and lay the whole thing flat the result is called a polyhedron map.
Conversely, you can take a polyhedron map, print it, cut it out, fold along the lines and attach at the tabs to create paper models of polyhedra.
This whizzlet has polyhedron nets for all five Platonic solids and several of the thirteen Archimedean solids. You can change the coloring scheme by selecting a new color and clicking on a polygon. Printing, not one of tk's strong points, is only partially implemented: it will generate a postscript file for you--you have to use some other tool to print it.
##+##########################################################################
#
# poly.tcl -- Draws polyhedron nets that you can print out, cut out, fold and
# join tabs to construct your own polyhedra. See http://www.korthalsaltes.com
# by Keith Vetter, March 5, 2003
#
package require Tk
set S(bwidget) [expr {! [catch {package require BWidget}]}] ;# For combobox
set S(title) "Polyhedron Nets"
# Info for each polyhedron:
# name,I => {<# faces> <tab size>}
# name,# {<face polygon type> <where> <sides w/ tabs> <color>}
# where => EITHER <angle for side 0> OR {<neighbor face #> <attach side>}
array set POLY {
Tetrahedron,I {4 .1}
Tetrahedron,0 {t 60 {0 2} blue} Tetrahedron,1 {t {0 1} {} yellow}
Tetrahedron,2 {t {1 1} {} red} Tetrahedron,3 {t {2 2} {2} green}
Cube,I {6 .2}
Cube,0 {s 0 {} yellow} Cube,1 {s {0 1} {} blue}
Cube,2 {s {0 2} {1 3} red} Cube,3 {s {2 2} {1 2} yellow}
Cube,4 {s {0 3} {2} blue} Cube,5 {s {0 0} {1 3} red}
Octahedron,I {8 .2}
Octahedron,0 {t 60 {} red} Octahedron,1 {t {0 1} {} yellow}
Octahedron,2 {t {1 1} {} cyan} Octahedron,3 {t {2 2} {} blue}
Octahedron,4 {t {3 1} {} green} Octahedron,5 {t {0 2} {2} violet}
Octahedron,6 {t {1 2} {1 2} orange} Octahedron,7 {t {2 1} {1 2} purple}
Icosahedron,I {20 .2}
Icosahedron,0 {t 60 {1} red} Icosahedron,1 {t {0 0} {} blue}
Icosahedron,2 {t {1 2} {1} cyan} Icosahedron,3 {t {1 1} {1} green}
Icosahedron,4 {t {2 2} {1} green} Icosahedron,5 {t {4 2} {} yellow}
Icosahedron,6 {t {5 1} {} blue} Icosahedron,7 {t {6 1} {2} cyan}
Icosahedron,8 {t {7 1} {2} red} Icosahedron,9 {t {3 2} {1} red}
Icosahedron,10 {t {9 2} {} yellow} Icosahedron,11 {t {10 1} {} blue}
Icosahedron,12 {t {11 1} {2} green} Icosahedron,13 {t {12 1} {2} cyan}
Icosahedron,14 {t {0 2} {1} cyan} Icosahedron,15 {t {14 2} {} yellow}
Icosahedron,16 {t {15 1} {} blue} Icosahedron,17 {t {16 1} {} red}
Icosahedron,18 {t {17 1} {2} green} Icosahedron,19 {t {17 2} {} yellow}
Dodecahedron,I {12 .2}
Dodecahedron,0 {p 108 {} yellow} Dodecahedron,1 {p {0 0} {4} blue}
Dodecahedron,2 {p {0 1} {4} red} Dodecahedron,3 {p {0 2} {4} blue}
Dodecahedron,4 {p {0 3} {4} green} Dodecahedron,5 {p {0 4} {4} red}
Dodecahedron,6 {p {1 3} {2 3 4} yellow} Dodecahedron,7 {p {2 3} {3 4} green}
Dodecahedron,8 {p {4 3} {2 3 4} yellow} Dodecahedron,9 {p {3 3} {2 3 4} red}
Dodecahedron,10 {p {5 3} {2 3 4} green} Dodecahedron,11 {p {7 2} {} blue}
Cubeoctahedron,I {14 .2}
Cubeoctahedron,0 {s 90 {} yellow} Cubeoctahedron,1 {t {0 2} {} blue}
Cubeoctahedron,2 {s {1 2} {3} yellow} Cubeoctahedron,3 {t {2 2} {1 2} blue}
Cubeoctahedron,4 {t {0 1} {} blue} Cubeoctahedron,5 {s {4 2} {3} yellow}
Cubeoctahedron,6 {t {5 2} {1 2} blue} Cubeoctahedron,7 {t {0 0} {} blue}
Cubeoctahedron,8 {s {7 2} {3} yellow} Cubeoctahedron,9 {t {8 2} {1 2} blue}
Cubeoctahedron,10 {t {0 3} {} blue} Cubeoctahedron,11 {s {10 2} {3} yellow}
Cubeoctahedron,12 {t {11 2} {2} blue} Cubeoctahedron,13 {s {12 1} {} yellow}
Truncated\ Tetrahedron,I {8 .2}
Truncated\ Tetrahedron,0 {h 120 {} green}
Truncated\ Tetrahedron,1 {h {0 0} {3 4 5} blue}
Truncated\ Tetrahedron,2 {t {0 1} {2} yellow}
Truncated\ Tetrahedron,3 {h {0 2} {4 5} cyan}
Truncated\ Tetrahedron,4 {t {3 3} {} yellow}
Truncated\ Tetrahedron,5 {t {0 3} {2} yellow}
Truncated\ Tetrahedron,6 {h {0 4} {3 4 5} red}
Truncated\ Tetrahedron,7 {t {0 5} {2} yellow}
Rhombicuboctahedron,I {26 .2}
Rhombicuboctahedron,0 {s 180 {0} green}
Rhombicuboctahedron,1 {t {0 1} {1} blue}
Rhombicuboctahedron,2 {t {0 3} {2} blue}
Rhombicuboctahedron,3 {s {0 2} {} red}
Rhombicuboctahedron,4 {s {3 1} {1 2} green}
Rhombicuboctahedron,5 {s {3 3} {2 3} green}
Rhombicuboctahedron,6 {s {3 2} {} green}
Rhombicuboctahedron,7 {t {6 1} {1} blue}
Rhombicuboctahedron,8 {t {6 3} {2} blue}
Rhombicuboctahedron,9 {s {6 2} {} red}
Rhombicuboctahedron,10 {s {9 1} {1} green}
Rhombicuboctahedron,11 {s {9 3} {3} green}
Rhombicuboctahedron,12 {s {10 2} {} red}
Rhombicuboctahedron,13 {s {11 2} {} red}
Rhombicuboctahedron,14 {s {9 2} {} green}
Rhombicuboctahedron,15 {t {14 1} {1} blue}
Rhombicuboctahedron,16 {t {14 3} {2} blue}
Rhombicuboctahedron,17 {s {14 2} {} red}
Rhombicuboctahedron,18 {s {17 1} {1 2} green}
Rhombicuboctahedron,19 {s {17 3} {2 3} green}
Rhombicuboctahedron,20 {s {17 2} {} green}
Rhombicuboctahedron,21 {t {20 1} {1} blue}
Rhombicuboctahedron,22 {t {20 3} {2} blue}
Rhombicuboctahedron,23 {s {20 2} {} red}
Rhombicuboctahedron,24 {s {23 1} {1 2} green}
Rhombicuboctahedron,25 {s {23 3} {2 3} green}
Truncated\ Octahedron,I {14 .2}
Truncated\ Octahedron,0 {h 180 {1 5} green}
Truncated\ Octahedron,1 {h {0 3} {} cyan}
Truncated\ Octahedron,2 {s {0 0} {} yellow}
Truncated\ Octahedron,3 {s {1 1} {1 2} yellow}
Truncated\ Octahedron,4 {s {1 3} {2} yellow}
Truncated\ Octahedron,5 {s {1 5} {2 3} yellow}
Truncated\ Octahedron,6 {h {1 2} {1 2 3 4 5} blue}
Truncated\ Octahedron,7 {h {1 4} {1 2 3 4 5} red}
Truncated\ Octahedron,8 {h {2 2} {} cyan}
Truncated\ Octahedron,9 {s {8 2} {1} yellow}
Truncated\ Octahedron,10 {s {8 4} {3} yellow}
Truncated\ Octahedron,11 {h {8 1} {1} blue}
Truncated\ Octahedron,12 {h {8 3} {1 5} green}
Truncated\ Octahedron,13 {h {8 5} {} red}
Truncated\ Cube,I {14 .4}
Truncated\ Cube,0 {o 180 {0 1 5 6 7} yellow}
Truncated\ Cube,1 {t {0 2} {} red}
Truncated\ Cube,2 {t {0 4} {} red}
Truncated\ Cube,3 {o {1 1} {} cyan}
Truncated\ Cube,4 {t {3 2} {} red}
Truncated\ Cube,5 {t {3 4} {} red}
Truncated\ Cube,6 {t {3 6} {} red}
Truncated\ Cube,7 {o {2 2} {} cyan}
Truncated\ Cube,8 {o {0 3} {1 2 3 6 7} green}
Truncated\ Cube,9 {o {8 4} {1 2 3 6 7} yellow}
Truncated\ Cube,10 {o {9 4} {1 3 6 7} green}
Truncated\ Cube,11 {t {8 5} {2} red}
Truncated\ Cube,12 {t {9 5} {2} red}
Truncated\ Cube,13 {t {10 5} {2} red}
Truncated\ Cubeoctahedron,I {22 .4}
Truncated\ Cubeoctahedron,0 {o 180 {0 1 7} cyan}
Truncated\ Cubeoctahedron,1 {s {0 2} {1} yellow}
Truncated\ Cubeoctahedron,2 {o {1 2} {} cyan}
Truncated\ Cubeoctahedron,3 {s {0 6} {3} yellow}
Truncated\ Cubeoctahedron,4 {o {3 2} {} cyan}
Truncated\ Cubeoctahedron,5 {s {0 4} {} yellow}
Truncated\ Cubeoctahedron,6 {h {5 1} {1 2 3} red}
Truncated\ Cubeoctahedron,7 {h {5 3} {3 4 5} red}
Truncated\ Cubeoctahedron,8 {o {5 2} {1 7} cyan}
Truncated\ Cubeoctahedron,9 {s {8 2} {1 2} yellow}
Truncated\ Cubeoctahedron,10 {s {8 6} {2 3} yellow}
Truncated\ Cubeoctahedron,11 {s {8 4} {} yellow}
Truncated\ Cubeoctahedron,12 {h {11 1} {1 2 3} red}
Truncated\ Cubeoctahedron,13 {h {11 3} {3 4 5} red}
Truncated\ Cubeoctahedron,14 {o {11 2} {1 7} cyan}
Truncated\ Cubeoctahedron,15 {s {14 2} {1 2} yellow}
Truncated\ Cubeoctahedron,16 {s {14 6} {2 3} yellow}
Truncated\ Cubeoctahedron,17 {s {14 4} {} yellow}
Truncated\ Cubeoctahedron,18 {h {17 1} {1 2 3} red}
Truncated\ Cubeoctahedron,19 {h {17 3} {3 4 5} red}
Truncated\ Cubeoctahedron,20 {o {17 2} {1 7} cyan}
Truncated\ Cubeoctahedron,21 {s {20 2} {1 2} yellow}
Truncated\ Cubeoctahedron,22 {s {20 6} {2 3} yellow}
}
#set len [llength [array names POLY "Truncated\ Cubeoctahedron,*"]]
#set POLY(Truncated\ Cubeoctahedron,I) [list [incr len -1] .3]
;# Exterior angle and sides for various polygons
array set polygon {t {120 3} s {90 4} p {72 5} h {60 6} o {45 8}}
proc DoDisplay {} {
wm title . $::S(title)
pack [frame .ctrl -relief ridge -bd 2 -padx 5 -pady 5] \
-side right -fill both -ipady 5
pack [frame .top -relief raised -bd 2] -side top -fill x
pack [frame .screen -bd 2 -relief raised] -side top -fill both -expand 1
canvas .c -relief raised -borderwidth 0 -height 500 -width 500 \
-highlightthickness 0
label .msg -bg [.c cget -bg] -bd 2 -highlightthickness 0 \
-textvariable S(type) -font {{Times Roman} 18 bold}
pack .msg -in .screen -side top -fill x -expand 0
pack .c -in .screen -side top -fill both -expand 1
set ::S(color) blue
set colors {red orange yellow green darkblue blue cyan purple violet white}
lappend colors [lindex [.c config -bg] 3] black
foreach color $colors {
radiobutton .top.b$color -width 1 -padx 0 -pady 0 -bg $color \
-variable ::S(color) -value $color
}
eval pack [winfo children .top] -side left -fill y
bind .c <Configure> {CanvasCenter %W %h %w}
bind all <Alt-c> {console show}
DoCtrlFrame
update
}
proc DoCtrlFrame {} {
global S
label .ltype -text "Polyhedron Type"
.ltype configure -width 15 \
-font "[font actual [.ltype cget -font]] -weight bold"
if {$S(bwidget)} {
ComboBox .type -textvariable S(type) -editable 0 -values [GetPTypes] \
-exportselection 0 -justify center -takefocus 0
grid .ltype - -in .ctrl -row 1 -sticky ew
grid .type - -in .ctrl -row 2 -sticky ew
} else {
eval tk_optionMenu .type S(type) [GetPTypes]
.type configure -width 20 -font [.ltype cget -font]
grid .type - -in .ctrl -row 1 -sticky ew
}
trace add variable S(type) write DrawNet
button .next -text Next -command {NextPoly 1}
button .prev -text Prev -command {NextPoly -1}
set txt "Print on heavy paper.\nFold all lines backwards."
append txt "\nAttach the white tabs."
label .instr -text $txt -font [.ltype cget -font] -justify left -anchor w
button .post -text PostScript -command PrintIt
button .about -text About -command About
grid .prev .next -in .ctrl -sticky ew
grid rowconfigure .ctrl 20 -minsize 100
grid .instr - -in .ctrl -row 21
grid rowconfigure .ctrl 50 -weight 1
grid .post - -in .ctrl -row 100 -sticky ew
grid .about - -in .ctrl -row 101 -sticky ew
}
proc GetPTypes {} {
set ptypes {Tetrahedron Cube Octahedron Icosahedron Dodecahedron}
foreach a [lsort -dictionary [array names ::POLY *,I]] {
set type [lindex [split $a ","] 0]
if {[lsearch $ptypes $type] > -1} continue ;# No duplicates
lappend ptypes $type
}
return $ptypes
}
proc CanvasCenter {W h w} {
foreach h [expr {$h / 2.0}] w [expr {$w / 2.0}] break
$W config -scrollregion [list -$w -$h $w $h]
ScaleIt
}
# DrawNet -- draws the net for the current polyhedron
proc DrawNet {args} {
global POLY V S
.c delete all
catch {unset V}
foreach {faces S(tabsize)} $POLY($S(type),I) break
set S(len) 100
for {set face 0} {$face < $faces} {incr face} {
foreach {type where} $POLY($S(type),$face) break
GetVertices $type $where $face
}
CenterNet ;# Shift to center net image
DrawFaces $S(type)
DrawTabs $S(type)
ScaleIt
}
proc DrawFaces {ptype} {
global POLY V
set faces [lindex $POLY($ptype,I) 0] ;# How many faces
for {set face 0} {$face < $faces} {incr face} {
set xy [GetFaceXY $face]
set color [lindex $POLY($ptype,$face) 3]
.c create poly $xy -tag [list poly f$face] -fill $color -outline black
.c bind f$face <1> {.c itemconfig current -fill $S(color)}
}
}
proc DrawTabs {ptype} {
global POLY S
set faces [lindex $POLY($ptype,I) 0] ;# How many faces
for {set face 0} {$face < $faces} {incr face} {
set tabs [lindex $POLY($ptype,$face) 2]
foreach tab $tabs {
foreach {p0 p1} [GetSideXY $face $tab] break
set v1 [RotateAdd $p1 $p0 120 $S(tabsize)]
set v2 [RotateAdd $p0 $p1 -120 $S(tabsize)]
set xy [concat $p0 $v1 $v2 $p1]
.c create poly $xy -tag [list poly tab] -fill white -outline black
}
}
.c lower tab
}
proc GetFaceXY {face} {
global V
set num [llength [array names V $face,*]]
set xy {}
for {set i 0} {$i < $num} {incr i} {
set xy [concat $xy $V($face,$i)]
}
return $xy
}
proc GetSideXY {face n} {
global V
set n2 [expr {$n + 1}]
if {! [info exists V($face,$n2)]} {set n2 0}
return [list $V($face,$n) $V($face,$n2)]
}
# GetVertices -- populates V with all vertex info for every face
proc GetVertices {type where face} {
global S V polygon
foreach {angle num} $polygon($type) break
if {[llength $where] == 1} { ;# First polygon
set V($face,0) {0 0}
set V($face,1) [RotateC [list $S(len) 0] -$where]
} else { ;# Polygon attached to another
foreach {prev side} $where break
foreach [list V($face,1) V($face,0)] [GetSideXY $prev $side] break
}
set p0 $V($face,0)
set p1 $V($face,1)
for {set i 2} {$i < $num} {incr i} {
set V($face,$i) [RotateAdd $p0 $p1 $angle]
set p0 $p1
set p1 $V($face,$i)
}
}
proc CenterNet {} {
global V
set an [array names V] ;# All the vertices
set a1 [lindex $an 0] ;# First vertex
set x0 [set x1 [lindex $V($a1) 0]] ;# Initial min/max values
set y0 [set y1 [lindex $V($a1) 1]]
foreach a $an {
foreach {x y} $V($a) break
if {$x < $x0} {set x0 $x} elseif {$x > $x1} {set x1 $x}
if {$y < $y0} {set y0 $y} elseif {$y > $y1} {set y1 $y}
}
set midx [expr {($x0 + $x1)/2}] ;# This should be the center
set midy [expr {($y0 + $y1)/2}]
foreach a $an {
foreach {x y} $V($a) break
set V($a) [list [expr {$x - $midx}] [expr {$y - $midy}]]
}
}
proc GetVector {p0 p1 {sc 1}} {
foreach {x0 y0} $p0 {x1 y1} $p1 break
return [list [expr {$sc * ($x1-$x0)}] [expr {$sc * ($y1-$y0)}]]
}
proc AddVector {v0 v1} {
foreach {x0 y0} $v0 {x1 y1} $v1 break
return [list [expr {$x1+$x0}] [expr {$y1+$y0}]]
}
proc RotateAdd {p0 p1 angle {sc 1}} {
set v [GetVector $p0 $p1 $sc]
set v [RotateC $v $angle]
return [AddVector $p1 $v]
}
# RotateC -- rotates vector v by beta degrees clockwise
proc RotateC {v beta} {
foreach {x y} $v break
set beta [expr {$beta * atan(1) * 4 / 180.0}]
set xx [expr {$x * cos($beta) - $y * sin($beta)}]
set yy [expr {$x * sin($beta) + $y * cos($beta)}]
return [list $xx $yy]
}
# ScaleIt -- scales everything to just fit on the canvas
proc ScaleIt {} {
set bbox [.c bbox poly]
if {[llength $bbox] == 0} return
foreach {x0 y0 x1 y1} [.c bbox poly] break
foreach w [winfo width .c] h [winfo height .c] break
set s [GetZoom $bbox $w $h 20]
if {$s == 0} return
.c scale poly 0 0 $s $s
}
proc GetZoom {bbox w h margin} {
foreach {x0 y0 x1 y1} [.c bbox poly] break
set pw [expr {$x1 - $x0}]
set ph [expr {$y1 - $y0}]
set sw [expr {double($w - $margin) / $pw}]
set sh [expr {double($h - $margin) / $ph}]
if {$sh < $sw} {set s $sh} else {set s $sw}
return $s
}
proc NextPoly {{dir 1}} {
global S
set ptypes [GetPTypes]
set len [llength $ptypes]
set n [lsearch $ptypes $S(type)]
set n [expr {($n + $dir) % $len}]
set S(type) [lindex $ptypes $n]
}
proc PrintIt {{zoom 1}} {
set height 1350
set width 975
set pageheight 9.0i
set pagewidth 6.5i
set fname [file join [pwd] polyhedron.ps]
set bbox [.c bbox all]
set zoom [GetZoom $bbox $width $height 0]
set width [expr {$width / $zoom}]
set height [expr {$height / $zoom}]
foreach {x0 y0 x1 y1} $bbox break
set x [expr {($x0 + $x1 - $width) / 2}] ;# Upper left corner
set y [expr {($y0 + $y1 - $height) / 2}]
set err [.c postscript -file $fname -rotate false -colormode color \
-x $x -y $y -width $width -height $height \
-pageheight $pageheight -pagewidth $pagewidth]
if {$err == ""} {
set msg "Created postscript version of the map in\n$fname"
} else {
set msg "Postscript creation error:\n$err"
}
tk_messageBox -title "Print" -message $msg
}
proc About {} {
set msg "$::S(title)\nby Keith Vetter, March 2003\n\n"
append msg "A polyhedron net is the planar unfolding of a polyhedron,\n"
append msg "with each polygon represents a face of the polyhedron.\n"
append msg "Included here are all five Platonic solids and several\n"
append msg "of the thirteen Archimedean solids.\n\n"
append msg "You can make a 3-D model of a polyhedron by printing\n"
append msg "out a net, cutting it out, folding along the lines and\n"
append msg "attaching the tabs. You can change the color of any\n"
append msg "face by selecting a color and clicking on the polygon.\n\n"
append msg "You cannot print directly from this program, but you can\n"
append msg "create a color postscript version the net which you can\n"
append msg "print using other tools."
tk_messageBox -title "About $::S(title)" -message $msg
}
DoDisplay
set S(type) [lindex [GetPTypes] [expr {int(rand() * [llength [GetPTypes]])}]]can you please show the shapes not the scripts for them thank you... - customer
-- Just cut and paste the code, then run the command "DoDisplay"
KPV sorry, looks like the last few lines got lost. I've fixed that so it should work by cutting and pasting.
MG 23/11/04 Removed a stupid/rude edit made by a twink.
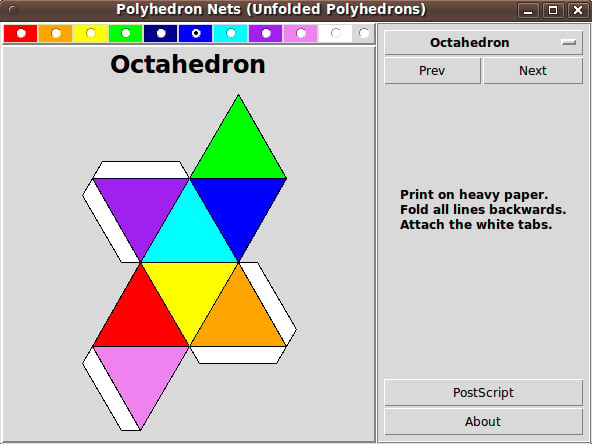
uniquename 2013jul29
This code could use an image to show what it produces:
(Thanks to 'gnome-screenshot', 'mtpaint', and ImageMagick 'convert' on Linux for, respectively, capturing the image to a PNG file, cropping the image, and converting the resulting PNG file to a JPEG file that was about 6 times smaller.)