Random Walk Equation Slot Calculator Example
Random Walk Equation Slot Calculator Example
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks,gold
- Comments Section
Preface
gold Here are some calculations using TCL expressions.
Introduction
gold 9/19/2021 Updated version. Here are TCL calculations on the Random Walk equation for stock market yields over years. The calculator for the random walk equation does not return a consistent fixed value from fixed constants, but does return a random value within the limits of its assumptions. Hence, the random walk calculator can be used to test expected gains and losses over an average of years or trials over time. The calculator will only work with integral years, as most of the returns are rated annually in the press. Essentially, in three years one can lose one's shirt, in 12 years one should either break even or gain or lose another shirt.
Alternate Concepts in Random Walks
The variable of total years (entry 7) is truncated or clipped to an integer for internal use inside the for procedure. For typical usage in stocks, removing the truncation would introduce a 10 to 20 percent error in the for procedure. But leaving the total years alone or non-truncation of total years as a real variable might be acceptable, fudged, or counter-scaled in some applications. Counter-scaling means taking the average result for integral total years and multiply by { total years in real variable } over { total years in truncation }. However, this issue was left out of the published calculator as "tricky code".
Gamblers Ruin Expectation E(P(N)) Application to Random Walks
An example from a wildly different subject is the Gamblers Ruin Expectation E(P(N)) application to Random Walks. The Gamblers Ruin Expectation as total probability over all individual N games is considered a part of the Random Walks topics. As defined here, expectation E(P(N)) is the combined probability over 1 or more games with a constant win probability for each game. The example here is 50 percent chance of winning for each game and complement percentage for losing. The Expectation E(P(N)) or Gamblers chance of going broke after N successive games is E(P(N)) = < 0.5 + 0.25 + 0.125 + . . Nth game >. The E(P(N) formula over the total games until finish is formula E(P(N)) = xpr {1. - (1./2.)^*$N} . The more games, the closer the E(P(N)) approaches 1. The Expectation E(P(N) for an infinte set of games is 1, meaning a dead loss over all total games. Check for 1 game is expr {0.5 } returns 0.5. Check for 2 games is expr {0.5 + 0.25 } returns 0.75Check for 3 games is expr {0.5 + 0.25 + 0.125 } returns 0.875 and ''expr { 1. - (1./2.)**3. } returns 0.875. Check for 4 games is expr { 1. - (1./2.)**4. } returns 0.9375. The Gamblers Expectation of win over all games or original flush state at E(P(N)) = 0 is not expected here, but still can not be ruled out.
Problem may be adaptable to medical uses, like effect of multiple shots or multiple doses of XXXX. Best Wishes,D
We believe that the TCL calculator entries or internal code could be adapted to simulate the Gamblers Ruin.
proc Gamblers_Ruin_Expectation {games probability_win} {
if { $games <1 } {
return -code error "The games must be 1 or larger "
}
expr {(1.-($probability_win**$games))} }
# game 1 0.5 returns 0.5
# game 2 0.5 returns 0.75
# game 3 0.5 returns 0.875
# game 4 0.5 returns 0.9375
# set win probability above 50% and win at Las Vegas
# game 3 0.6 returns 0.784
# game 3 0.6 returns 0.870Alternates
As as alternate way of using the calculator code and testing the concept, the monthly rates for good, normal, and bad months may loaded and the time period might be 8 months, 25 months, etc. For a monthly rate, one would divide some yearly rates by 12 months. With TCL procs in place, one could adapt a second (and copied!) calculation proc to divide the year rate by 12, compute the time as decimal years times 12, and then report total yield, converting months back into years.
In the testcases loaded in the calculator, the rates were set in a balanced hierarchy. The balanced hierarchy was {bad year rate} << {normal year rate } << {good year rate } or values -10X<<+5X<<+10X in triple ratio. This calculator is very flexible and the user might choose an unbalanced hierarchy. For example, a bad year might be the low positive rate for goverment or corporate notes with normal and good years in the stock market as values +2X<<+5X<<+10X. The experience of mankind has found that one year of bad luck can cancel seven years of good luck. So a philosopher or cynic might set an unbalanced hierarchy as values -7X<<+1X<<+2X, ref Joseph the Hebrew from the Bible. The user and taxpayer might find that the governments tax gains far more than reward losses, so an unbalanced hierarchy of values might be useful as values -10X<<+1X<<+7X, closer to the actual user taxes. The real benefit of the random walk equation is not measuring or predicting exact loss and gain for the user. A calculator of random rates can not solve exact loss and gain. But the use of the random walk equation allows the user to have a more realistic expection of possible losses and gains.
Push Button Operation
For the push buttons in the TCL calculator, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console to conventional texteditor. For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers should be cleared either on the clear button or on the next solve button.
Calculator Usage
The concepts of random yield are fairly simple and may be adapted to other cumulative effects like centimeters of rainfall over years, sand dune accumulation in feet over decades, crop yield in bushels over years, or even horseraces with handicaps. The calculator was written for stock yield and integer years, but any consistent time interval could be used like days, months, quarter years, decades, or centuries could be used.
pseudocode:Random walk equation
year rate = good year rate * term chance(1 in n)
plus normal year rate * term chance(1 in n)
plus bad year rate * term chance(1 in n)
plus place holder to keep from all zeroed terms
pseudocode: set chance terms initially to zero until activated.
pseudocode: if rand() < $side2 , set term1 1
pseudocode: if no chance terms fire, year of zero interest will result.
pseudocode: if chance<(1 in n) terms fire, year of calc. interest will result.
pseudocode: not all terms will fire on every period of time.
pseudocode: good/norm/bad years loaded as $side1,$side2,$side3 from form.
current = .01*$side1*$term1+.01*$side3*$term2+.01*$side5*$term3+.00000000001 } ]
pseudocode: add $current sum of terms for 1 to N years in for loop
pseudocode: and divide by N years from $side7 in form
pseudocode: load results into answer fields In planning any software, there is a need to develop testcases.
Testcase 1.
| quantity | number | units |
|---|---|---|
| interest rate for good year | 10. | percent |
| 1 in chance: | .333 | none |
| interest rate for normal year | 5 | percent |
| 1 in chance: | .333 | none |
| interest rate for bad year | -10 | percent |
| 1 in chance | .333 | none |
| 1 to N years: | 1 | |
| answer is random from -.1 to +.15 | percent |
Screenshots Section
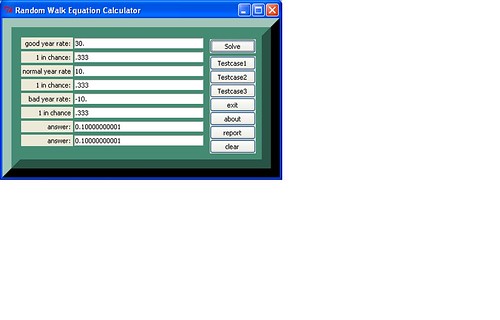
References:
- Random Walk Down Wall Street,by Burton G. Malkiel
- Random Walks, Gambler's Ruin, and the Quest for Jack or Jill
- RUIN PROBABILITY VIA SEVERAL NUMERICAL METHODS by Muhsin Tamturk
- Gambler’s Ruin Problem - John Boccio
- Gambler's Ruin
Appendix Code
appendix TCL programs and scripts
Pretty Print VERSION
# TCL source code follows
# pretty print from autoindentation and ased editor
# random walk equation V2
# written on Windows XP on TCL
# working under TCL version 8.6
# gold on TCL club, 2Dec2018
package require Tk
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
foreach {i name} { 1 {good year rate:} 2 {1 in chance:} 3 {normal year rate}
4 {1 in chance:} 5 {bad year rate:} 6 {1 in chance}
7 {1 to N years:} 8 { answer >> total random yield over N years :}
} {
label .frame.label$i -text $name -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1
}
proc about {} {
set msg "Calculator for Random Walk Equation V2.
from TCL "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg "Random Walk Equation Calculator V2
from TCL ,
# self help listing
# problem, Random Walk equation for stock market yields over years.
# Sum accumulation of good, normal, and bad rate conditions
# (ref stock fund yields)
# over time interval of integral years.
# 7 givens follow.
1) good year rate
2) 1 in chance
3) normal year rate
4) 1 in chance
5) bad year rate
6) 1 in chance
7) 1 to N years
The random walk equation does not return a consistent fixed value
from fixed constants, but does return a random value
within the limits of equation assumptions and constraints.
The calculator was written for stock yield and integer years,
but any consistent time interval could be used like
days, months, quarter years, decades, or centuries could be used.
The concepts of random yield are fairly simple and may be
adapted to other cumulative effects like centimeters of rainfall
over years, sand dune accumulation in feet over decades, crop yield
bushels over years, or even horseraces with handicaps.
The variable of total years (entry 7) is truncated or clipped
to an integer for use inside the for procedure.
# Recommended procedure is push testcase and fill frame,
# change first three entries etc, push solve,
# and then push report. Report allows copy and paste
# from console to conventional texteditor. For testcases
# testcase number is internal to the calculator and
# will not be printed until the report button is pushed
# for the current result numbers.
# >>> copyright notice <<<
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK license terms.
# Editorial rights and disclaimers
# retained under the TCL/TK license terms
# and will be defended as necessary in court.
Conventional text editor formulas or grabbed from internet
screens can be pasted into green console.
# gold on TCL Club, 2Dec2018 "
tk_messageBox -title "Self_Help" -message $msg }
proc intelligent5 { xx1 } {
global side1 side2 side3
global side4 side5 side6 side7 side8
set term1 0
set term2 0
set term3 0
set current 0
set chance1 [expr {1./$side2 }]
set totyears [expr {int($side7) }]
for {set i 0;} {$i<$totyears} {incr i} {
if { [ expr { rand() } ] <= $side2 } {set term1 1 }
if { [ expr { rand() } ] <= $side4 } {set term2 1 }
if { [ expr { rand() } ] <= $side6 } {set term3 1 }
set current [ expr { ($current*1.) +.01*$side1*$term1+.01*$side3*$term2+.01*$side5*$term3+.00000000001 } ]
}
set side7 $totyears
set side8 [expr {($current*1.)/$totyears }]
if { [ expr { abs($side8) } ] <= .0001 } {set side8 0 }
return $side8
}
proc calculate { } {
global answer2 testcase_number
global side1 side2 side3 side4 side5 side6 side7 side8
incr testcase_number
set answer2 5
set answer2 [ intelligent5 $side8 ]
set side8 $answer2
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff "
.frame.entry7 insert 0 "$gg "
.frame.entry8 insert 0 "$hh "
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8} {
.frame.entry$i delete 0 end
}
}
proc reportx {} {
global side1 side2 side3 side4 side5 side6 side7 side8
global testcase_number
console show;
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . "Report on console , cut and paste from console 2"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts "%| table |printed in| tcl format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| testcase number| $testcase_number||& "
puts "&| good year rate:| $side1 ||&"
puts "&| 1 in chance:| $side2||& "
puts "&| normal year rate:| $side3||& "
puts "&| 1 in chance :| $side4 ||&"
puts "&| bad year rate:| $side5||& "
puts "&| 1 in chance:| $side6 ||&"
puts "&| 1 to N years :| $side7 ||&"
puts "&| answer >> total random yield over N years :| $side8 ||&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 10. .333 5. .333 -10. .333 1. 1.}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 10. .333 5. .333 -10. .333 7.7 1. }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 10. .333 5. .333 -10. .333 8.5 1. }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command about
::ttk::button .self_help -text self_help -command { self_help }
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Random Walk Equation Calculator V2"
Comments Section
Please place any comments here, Thanks.
Q: What is your purpose in binding the motion event on your main window to execute the wm title command. I.e., this line:
bind . <Motion> {wm title . "Random Walk Equation Calculator "}The result of that binding is that every time you move the mouse, the "wm title" subcommand is called repeatedly. To set the window title, you just need to call "wm title . title" once, not on every event update upon mouse pointer motion.
Why do you define the procs interlinear, pol, errorx, and height5 when you do not appear to use them anywhere in the code presented? In examples, having extra bits defined that are not used adds noise that a reader has to expend effort upon only to later learn that he/she could have ignored that part. Keeping the example focused upon only that which is needed for just the example, and nothing more, makes for a more informative, and educational, example.
Note, the Tcl foreach command will iterate across plural lists in parallel. As a result, your set names ... foreach i loop could be written this way:
foreach i { 1 2 3 4 5 6 7 8 } \
name { {good year rate:} {1 in chance:} {normal year rate} {1 in chance:}
{bad year rate:} {1 in chance} {1 to N years:} { answer:} } {
label .frame.label$i -text $name -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1
}It will also iterate across a single list taking more than one element at a time. Your loop could also be written this way (with some whitespace sugar to make the relationship more apparent to a human reader):
foreach {i name} { 1 {good year rate:} 2 {1 in chance:} 3 {normal year rate}
4 {1 in chance:} 5 {bad year rate:} 6 {1 in chance}
7 {1 to N years:} 8 { answer:}
} {
label .frame.label$i -text $name -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1
}gold changes: deleted procs interlinear, pol, errorx, height5 and "pi" , replaced with wm title . title. Replaced foreach statement.
gold 9/27/2021. Switched some comment signs ;# to #. This a big file. Check earlier editions, if not compatible. Maybe obvious, but this page was written on Windows10 Tcl ports including ActiveTCL. I assume that the reader can cut and paste on screen, what the reader needs, and tootle on to his own project and own contribution pages to the TCL Wiki.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |