Sumerian Coefficients in the Pottery Factory and Calculator Demo Example
Sumerian Coefficients in the Pottery Factory and Calculator Demo Example
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 12DEC2018
- Sumerian Coefficients in the Pottery Factory and Calculator Demo Example
- Preface
- Introduction
- Appendix Code
- Comments Section
Preface
gold Here is some starter code for calculating fuel and dimensions of ancient pottery kilns. The impetus for these calculations was checking rated kiln capacity in some excavation reports and modern replicas. Most of the testcases involve replicas or models, using assumptions and rules of thumb .
Introduction
In the Sumerian coefficient lists, there are coefficients which were used in determining the fuel capacity of a Sumerian kiln and the daily work rates of the pottery workers. One coefficient is called "sa esir had ina kiriti" (coefficient pitch in kiln) which has a value of ~10. Culled from different lists, the kiln coefficients range 10/20 in base 60, and possibly represent different style kilns. The math problem is how this kiln coefficient was used in estimating kiln capacity and work rates. One difficulty is determining the effective power of the coefficient in base 60. For example, 20 could represent either 20*3600,20,20/60, 20/3600, or even 1/20. A complete math problem or explanation on kiln dimensions (L,W,H) is lacking.
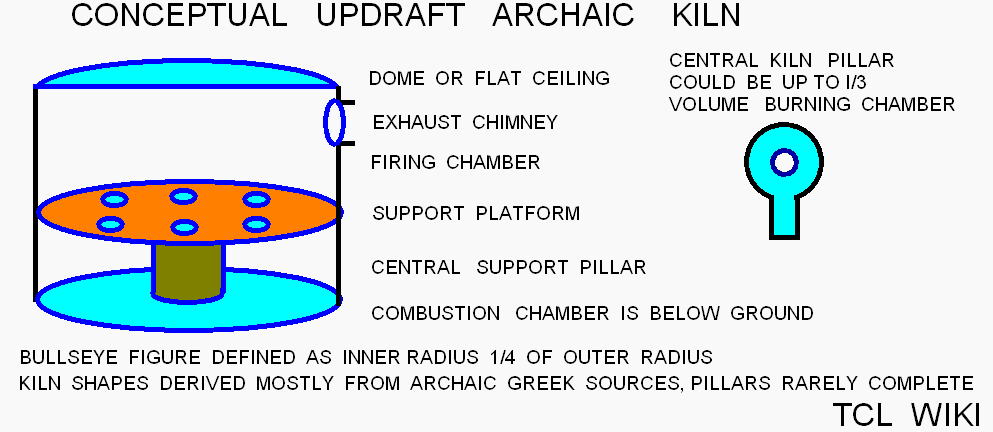
However, the Sumerian coefficient lists show the Sumerians busy with coefficients for computing the horizontal area of kiln figures or the volumes of possible kilns.. In general terms, some coefficients were used to convert a surface area sar (eg. square nindans in Sumerian usage) into a volume sar with units of gurs. A nindan equals 6 meters, a surface area sar about 36 square meters, and a volume gar about 0.3 cubic meters. The generic formula would be surface sars in nindan*nindan times coefficient equals volume sar in units of gurs. After a considerable amount of scratch paper, the Sumerians appear to be using daily fuel packing rate in volume gars. A complete and period text available on the dimensions of the various Sumerian kilns is lacking, but the various coefficients have been examined based on modeling the traditional native kilns and scaling available replicas.
While the Sumerians usually measured horizontal areas in square nindans for the kilns and grain bins, the problem is essentially the same: fitting circles or volume units into a fixed area or geometric figure. In modern terms, this is called a circle packing problem. One nindan equals 6 meters and a square nindan equals 36 square meters. A volume gur equals 0.3 cubic meters. One common size of kiln in the excavations was diameter 0.5 meters and height 0.5 meters, figures for below ground combustion chamber. The volume would be (1/4)*PI*D*D*H,.25*3.14*.5*.5*.5 or 0.098 cubic meters. In Sumerian terms, the volume would be 0.098/.3, decimal 0.3266 or 20/60 + 36/3600 volume gurs in base 60. The estimated coefficient 20:36 is within range of the 0;20:48:06 (in base 60) number on the clay tablets. One possibility is that the pitch and reed kiln coefficients represent the fraction of (fuel volume) / (burning chamber volume). At least some kilns had support pillars or walls within the burning chamber which would subtract from the total volume. Other kilns were single chamber kilns which filled up some of their volume with support shelves, wares, and ware props. In other words, the total volume of the chamber was not occupied with fuel. Also, it was found that coefficient*circumference* circumference* circumference equals nearly the amount of gurs in the burning chamber. The circumference cubed is not a likely formula, since use of cubed value has not been associated with a coefficient before. From other coefficients on the tablets, the daily work rate of excavations was 10/60 gurs and if the kiln fuel loading problem is analogous, the number of man work days to load the kiln fuel was (20.8/60)/ (10/60) or roughly 2 work days.
There is more than one theory on the kiln used by the reed workers. The reed workers cooked the reeds with lime to soften and bleach the reeds before weaving mats. In some cases, the reed workers may have dried their baskets in an oven to assure a dry and insect free product. Possibly, the reed workers made a sort of charcoal briquet or cooking fuel, baking green reeds in a special oven (eg. a charcoal kiln). Lets return to the original Sumarian phrase, "20_48_06 sa gir4 ad kup4". As others have remarked, the Sumerian/Akkadian script on the tablets is the most homonym filled language on earth. The Sumerian word "ad" could either be associated with reed (addatu, reed pith) or day's work (adu, sun come), or village (aduru, wall of reeds). Since the jobs as diverse as potters, ditch diggers, and basket weavers have their daily rate of work in the coefficient lists, there is at least some possibility that "ad" modifies "kupru" and refers to a daily task on the construction liquid asphalt. Also, its easier and closer to the meaning of a Sumerian noun-phrase to develop a full sentence, sic. "20_48_06 sa gir4 ad kup4" could mean: The 20_48_06 coefficient of? (kiln that burns reeds) is? a? (day's work) on? (construction liquid asphalt pitch). There are traditional kilns and replicas which still use the Sumerian and Greek designs, so the calculator empirical formulas are based on the known wood fuel/volume ratios.
From the contemporary and traditional kilns, the amount of heat energy needed to fire the known dimensions of Sumerian kilns can be estimated. Also from modern tests, the heat constants of burning wood/reeds/asphalt are 13.5/17/40 megajoules per (dry) kilogram. The 13.5 MJ/kg for wood is an average number based on scrap wood and uncovered woodlots, not completely dry wood. Rounding the Sumerian coefficient for burning reeds is 20/60 and the Sumerian coefficient for burning asphalt is 10/60. The Sumerians are probably multiplying the volume of the kiln burning chamber times the coefficient fraction to estimate the needed volume of fuel. Since the ratio of the heat constants (17/40 or 0.425) indicates that reeds supply roughly half the heat of asphalt, the mass of reeds to fire a kiln should be twice <(20/60)/(10/60)> that of asphalt. While there is more current documentation about burning wood in kilns than reeds or asphalt, some tentative calculations can be made with the Sumerian coefficients for reeds and asphalt. A kiln of 3 cubic meters volume would be roughly 3/.3 or 10 volume gurs. Using the asphalt coefficient, the needed asphalt fuel would be 10 gurs * (10/60) or 1.66 gurs. Assuming the specific gravity of 1 for asphalt, this would be 1.66*.3*1.*300. , 149.39 kilograms of asphalt. In Sumerian mass units, this would be 149.9/.4977 or 301 mannas. For the fuel reeds, the calculation would be 10 gurs * (20/60), 300 kilograms, or 600 mannas of reeds. From other tablets, the Sumerians counted a bundle of reeds or manload of reeds as 20 manas, so the amount of reeds would be 600 manas/20 or 30 bundles.
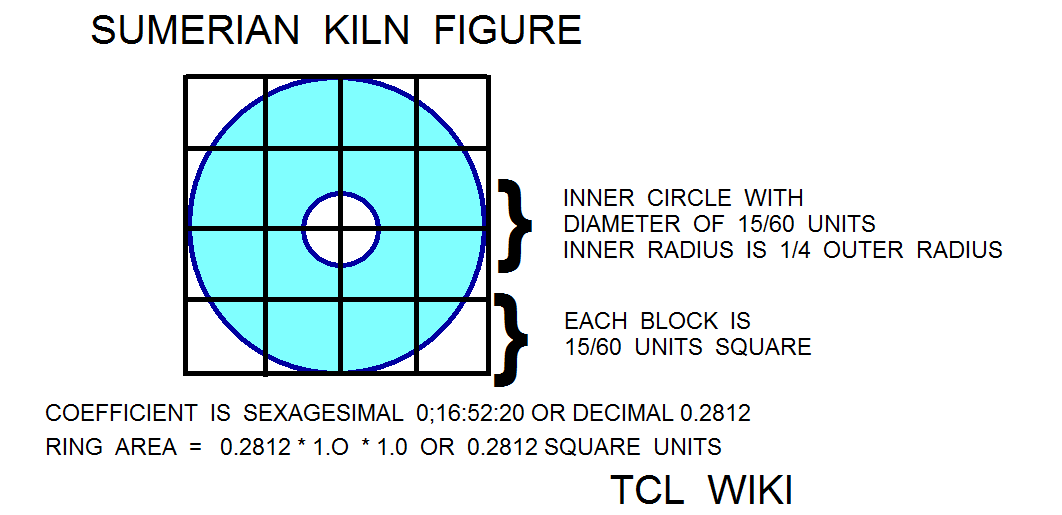
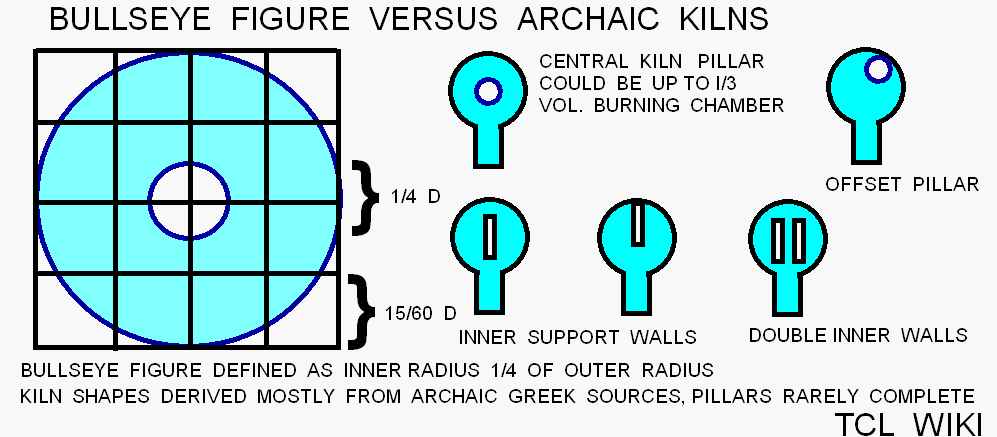
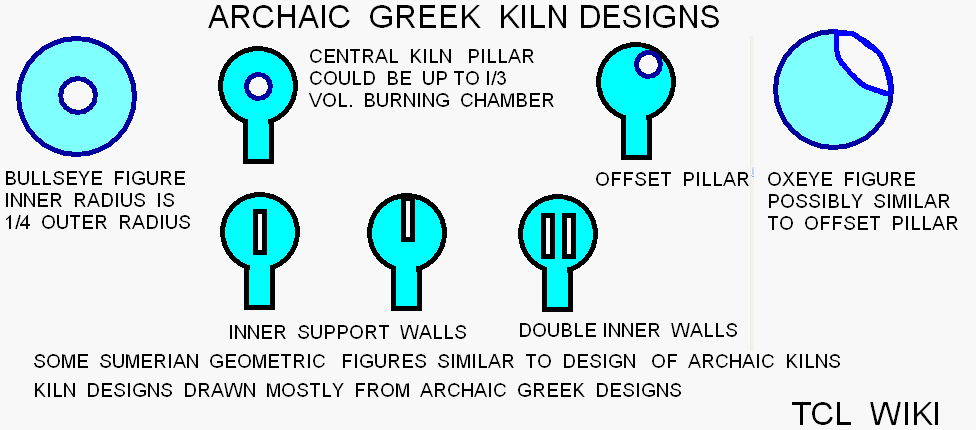
One topic of interest is the efficiency of kilns, Sumerian or otherwise. For example, one tenth of the energy used in contemporary China is burned making bricks in kilns and similar proportions in other industrial countries. The efficiency of a kiln is measured by the applied heat on the clay mass over the total heat used, usually in percent of applied heat over total heat or in megajoules per 1000 kilograms of pottery. While the numbers are not complete in the Sumerian case, one can look at the features of the Sumerian cylindrical kilns and estimate an ideal heat budget. Starting with an equal diameter and height burning chamber, then find the ideal proportion of heat sharing in a cylinder. As in a Sumerian math problem, the clay mass will be a central pillar with a radius and diameter at 1/4 that of the surrounding kiln. The diameter and height of the kiln are both 1. The height of the clay mass will be 1/2 the diameter of the kiln. In an ideal heat engine, 1/2 the total heat will remain in the kiln and 1/2 will leave up the chimney. The next math problem is finding the proportions of the heat that remains in the kiln.
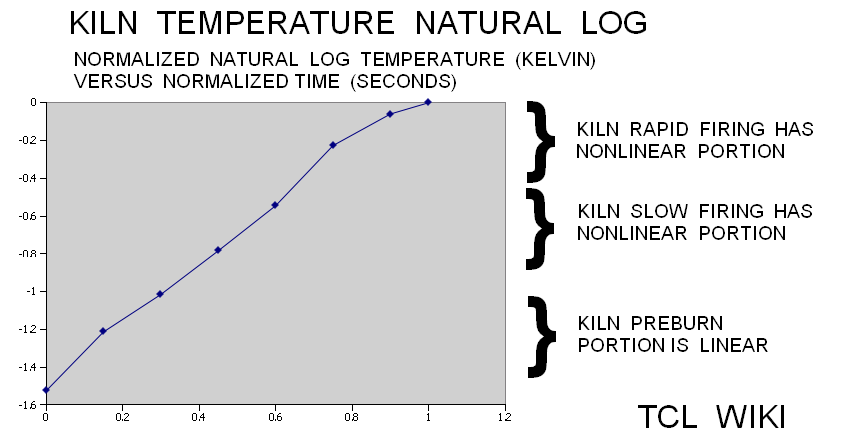
Of the heat that remains in the kiln, the transfer of heat to the pottery is ideally proportional to the surface area of the clay mass over the internal surface area of the cylindrical kiln. So estimate the ratio clay surface area over ( top + bottom + wall), 2*pi*r2*h2/ ((pi*r1*r1)+(pi*r1*r1)+ (2*pi*r1*r1)),substituting r2= r1/2 and h2=h1/2, leading to 2*pi*(r1/2)*(h1/2) over 2*pi*r1*(r1+h1), reducing to (1/4+h1/2)/(r1+h1). Since h1=2r1, the ratio is (1/4+(2r1/2))/(r1+2r1), (1+4r1)/12r1 evaluated at r1=.5 or 3/6. We can fraction with 3*x+6*x = 1/2 total heat or x=1/18, so we can develop fractions 6/18, 3/18, 9/18 for the terms of total heat. For heat budgeting, the total heat equals 6/18 (walls+top+bottom) +3/18(clay mass) + 9/18 (outlet air). Similarly, the (top + bottom) over inner wall surface are (pi*r1*r1+pi*r1*r1)/(2*pi*r1*h1), where h1=1,(r1*r1/r1) where r1 evals at .5, and leads to a 1:2 ratio for cylinder ends to inner wall. Accounting for the walls and top, total heat = 4/18 (walls) + top(1/18) + bottom(1/18) +3/18(clay mass) + 9/18 (outlet air). The proportion 3/18, decimal 0.166 or 17 percent is the maximum efficiency expected from a circular batch kiln. Most of the circular kilns fall short of this ideal because the clay mass or wares do not receive the best exposure to the hot air flow. Still, any more sophisticated analysis or suggested improvements will have account for heat budget or reduce the terms and losses. ( The heat flux and budget of the kiln has nonlinear terms over time. )
The price of fired brick in Sumerian times might also be indicative of energy costs per brick. In Ur III, 1 gur of barley brought 288 bricks from the brickmaker. In the equivalence texts, the brickmaker was paid 1 ban or (1/4) gur of barley a day and daily work quota was 288 bricks a day. So some equations can be set up. 1 gur barley = (1/4 gur)payday + ( price of fuel for 288 bricks), 1 gur = price of 600 manas of asphalt, and 1 mana = 0.4977 kg. Subtraction gives 3/4 gur = price of fuel for 288 bricks. Substituting , 3/4 gur will buy (3/4)*600 or 450 mannas of asphalt = 288 * bricks. So, 1 brick = 450/288 or 1.56 manas of asphalt per brick or 1.56*.4977, 0.776 kilograms of asphalt per brick. 0.776 kilograms * 40 MJ/kg fuel gives 31.04 MJ per brick. A brick weighed 7.4 kilograms, so the applied heat of the brick was 31.4/7.4 or 4.3 MJ/kg.
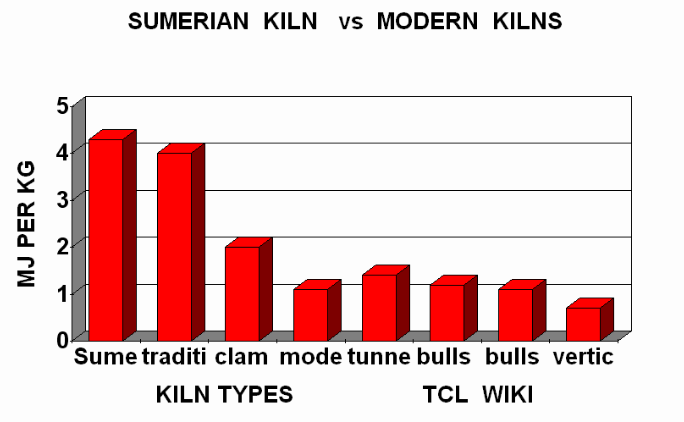
Possible ratios and fractions for the unfired pottery clay mass in Sumerian circular kilns can be developed from the traditional kilns and rules of thumb. One style of clamp kilns uses a formula ratio of fuel to clay mass as 400 kilograms of coal to 1000 green bricks, each green brick weighing 3.6 kilograms. So the ratio of fuel is 400/(1000*3.6), 0.11 coal kilograms per clay mass. For comparison, the British equivalent formulas from the 1880s was 454 kilograms coal per 1000 soft bricks and 907 kilograms coal per 1000 hard vitrified bricks, figuring green bricks at 3.8 kilograms. The coal has a heating value of 25 Megajoules per kilogram, so the process heat per kilogram is (400*25)/(1000*3.6) or 2.7 MJ/kg. The finished brick has lost moisture and weighs about 3 kg. Most of the traditional kilns have a range of 4 to 6 MJ/kg. Actually, the MJ/kg per brick is the most consistent parameter reported on traditional kilns, since the fuels, ceramic shapes, and brick weights vary so much. The traditional circular kilns usually fire from 500 to 1200 kilograms of green clay for a kiln of 3 cubic meters. Figuring the volume of the green clay as 2500 kilograms per cubic meter, the traditional fractions of clay volume to kiln volume would be from (500/2500)/3 to (1200/2500)/3, decimal 0.066 to 0.16, or 4/60 to 10/60 in base sixty. Another approach is (fuel & energy) /clay ratio. Previously it was found that the reed burning kiln (gir4) of 3 cubic meters would need 300 kilograms of reeds, which has a heat equivalent of 17 MJ/kg * 300 kg or 5100 MJ. The asphalt kiln (kirim) would need 149.4 kilograms of asphalt fuel, which is 40MJ/kg *149.4 or 5976 MJ. Taking the clay heat ratio and the 6 MJ/kg from the traditional kilns, the reed kiln would need (5100 MJ)/(6 MJ per kg) or 850 kg of green clay. The asphalt kiln would need (5976 MJ) / (6 MJ per kg) or 1000 kg of green clay. Returning to volume equivalents, the volume fraction of clay over kiln volume would range from (850/2500)/3 to (1000/2500)/3, decimal 0.111 to 0.133, or 6.6/60 (reeds) to 8/60 (asphalt). Of course, these brick calculations are really order of magnitude calculations. But we realized that the coefficients "20_48_06 sa gir4 ad kup4" for the reed kiln and "10_45_06 esir2 had5 a sa in-na ki-ri-im" for the asphalt kiln share a common 06 digit. Possibly 06 is really a separate coefficient and represents the fraction of clay volume over the kiln volume as 6/60. If the kiln coefficient lines are three separate numbers, then possibly coefficient values 45/48 refers to the top end area of a cylindrical kiln (3 for pi, (45/60) *D*D, in area sars) or the volume calculations for the cylindrical kiln (3 for pi, (45/60)*D*D*H, in volume gurs).
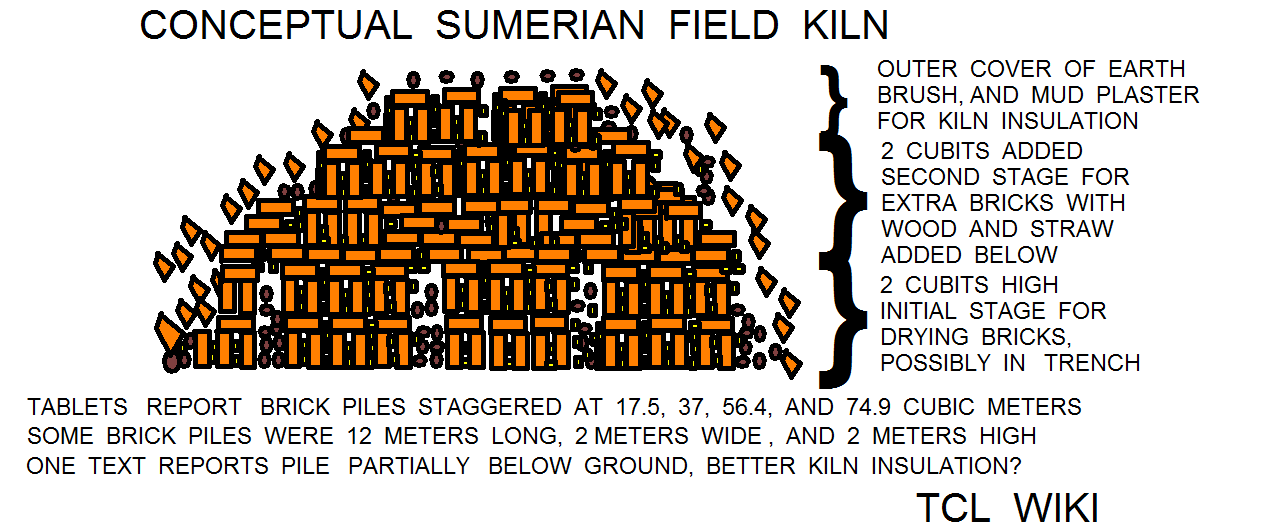
Some parameters from the modern clamp kiln can be estimated for some scale considerations on Sumerian volumes of brick piles or possible field kilns. The 1880’s British clamp kiln was LWH 60/11/12 feet or 18.29/3.353/3.657 meters and contained 8E4 English green bricks of about 8.6 kg each. The volume of the British clamp kiln here would be roughly 224 cubic meters, 18.29*3.353*3.657. The clay mass was about (8E4*3.8) or 3.04E5 kilograms and would require 3.63E4 kg of coal. In the British clamp kiln, there are upper limits to width at 4 meters to pitch wood or fuel through tunnels to the inside of the kiln and upper limits to height at 4 meters as to avoid extensive scaffolding. There is no particular upper limit to the British clamp length and volume, but given a width of about 4 meters, a kiln length below 4 meters would probably waste fuel.
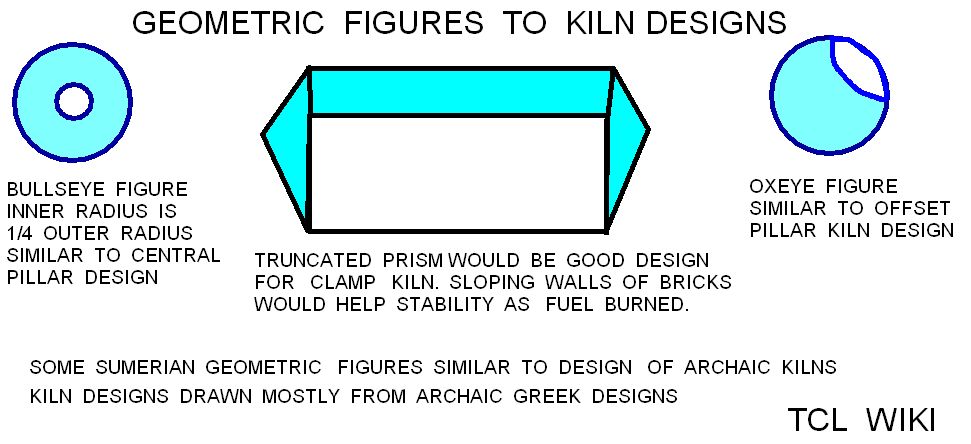
For the Sumerian evidence of possible field and clamp kilns, there are a number of tablets which discuss a volume of 9 sar bricks and other possible volumes from 0.44 to 810 cubic meters. The tablet VAT6598 discusses a wall (e-gar) that was 4 volume sars and contained 9 sar bricks or 1.2 cubic meters. Tablet YBC4708 is a problem text for a truncated brick pyramid of 1.5 volume sar or 0.44 cubic meters. The tablet YBC4708 concerns a brick pile of 30/9/3 meters and a volume of 810 cubic meters (uncertain if kiln?). Another text mentions an im-gir4 (mud kiln) of 9 brick sar or 6480 bricks, which appears to be a clamp kiln. The volume of the mud kiln would be 6480 *.33*.33*.08 or 56.4 cubic meters. One text mentions a truncated triangular prism that amounted to 9 sar baked bricks. The truncated triangular prism would be a particularly good form for a clamp kiln, since the offset or sloping inward walls offer better stability while the clamp kiln burns and loses some supporting volume. The value of 9 brick sar alone has shown up in several brick porting and receiving texts and math problems, though not always in obvious context with kilns, prism shapes, or fuel. One text mentions receiving a total of 36000 bricks and 9 sar bricks, implying 9 sar bricks was a special unit. Based mostly on the problem text of the truncated triangular prism, the 9 sar values in the tablets appear to endorse the best candidate volume for a field or clamp kiln.
A wage budget for a Sumerian im-gir4 (mud kiln) can be estimated from the given volume and the daily wage figures the Sumerians were computing in the coefficient and equivalency lists. The third month of the Sumerian calendar was iti sig4.ga ( month of forming bricks). The third month roughly the month of May, after the month of the yoked ox when the hired men came back from plowing and sowing fields. The mud bricks were normally set out before and dried during the hot season. Also, straw, reeds, and brush would be available for fuel. While building a clamp kiln would not be a job for a single man or single work day, some of the coefficients for digging clay of 6 cubic meters daily, bringing mud of 4 cubic meters daily, mixing earth of 3 cubic meters daily, and especially the mud kiln of 6480 bricks are approaching the magnitude of a small brick clamp. According to the metrology lists, a volume sar would contain 1944 baked bricks of the square top type (LWH .33/.33/.08 meters). We can try to set up a budget for a small clamp kiln. The volume of the mud kiln would be 6480 *.33*.33*.08 or 56.4 cubic meters. The total daily work on the clay mass would be (56.4/6) 9.4 days digging clay > (56.4/4) 14.1 days porting clay> (56.4/3) 18.8 days mixing clay> (56.4/(288*.33*.33*.08)) 24.47 days forming bricks > (4?) days loading kiln and firing bricks. The sum of these days times the minimum wage ( 9.4+14.1+18.8+24.47+4)*(1/8 gur barley)+ 2.3 gurs worth of fuel or 11.15 barley gurs. 11.15 barley gurs for 6480 bricks should be near the price of baked bricks. .In UR111, 1 gur barley bought 8_24 bricks or 504 burnt bricks, proportionally the bricks from the mud kiln should bring (6480*1. gur)/504 or 12.86 barley gurs. The delta price is 12.86-11.15 or 1.7 barley gurs, but some of the skilled workmen and foremen received 0.5 - 1 gur a day, so the budget is reasonably close. Actually, the daily task of brick firing and daily wage at the kiln as opposed to general “making brick” needs to be firmed up better.
For the possible pitch/clay ratio of a field kiln, some trial calculations for equivalent fuels can be made based on the British clamp kiln of the 1880's. The British equivalent formulas from the 1880s was 454 kilograms coal per 1000 soft bricks and 907 kilograms coal per 1000 hard vitrified bricks, figuring green bricks at 3.8 kilograms. These British equivalent formulas were still being used in former commonwealth countries as late as 2000 CE, prior to the Kyoto Protocols on Greenhouse Gases. These equivalent calculations have some interest for replica kilns, since some historic fuels are no longer available or effectively outlawed. By mass, the British formula is 454 kilograms coal over 1000*3.8 kilograms, 454/3800, 0.11947 or 7.16/60. By mass the British formula is 907 kilograms coal over 1000*3.8 kilograms, 907/3800, 0.2386 or 14/60 mass fraction. The volume fractions can be calculated using specific gravity, 1.3 for coal and 1.9 for clay which are equivalent to coal =1300kg/cubic meters and clay=1900kg/cubic meters. The coal/clay volume fraction for the soft bricks would be 454*1300/3800*1900= .0817, or 4.9/60 volume fraction. The coal/clay volume fraction for the hard bricks would be 907*1300/3800*1900= 0.1633, 9.7/60 volume fraction. These coal/clay fractions can be converted into equivalent heating units of bunker oil, which is very close to dry bitumen in density and heating value. The clay mass (3800 kg) can be converted into a volume, (3800 kg/1900 kg/cm) *1000 liters/cm, 2000 liters of clay. Using 794.77 liters of bunker oil for 1000 kg of coal, the soft brick volume fraction for bunker oil liters/ clay liters would be (360 liters of oil) over (2000 liters of clay), 360/2000, decimal 0.18, or 10.79/60, volume fraction. The hard brick volume fraction for bunker oil liters/ clay liters would be (720 liters of oil) over (2000 liters of clay), 720/2000, decimal 0.36, or 21.6/60 volume fraction. The majority of the extant UR111 clay bricks probably could have been fired with the soft brick fuel ratio, but none of the calculations here rule out higher fuel rates for other ceramics, metals, frits, and artificial stones.
There was not much accessible on renewable fuel reeds (gi bar) or acacia firewood, but some considerations can be extrapolated from published tablets and equivalency lists. The daily norm for reed fodder was 3 bales per day or 15 bundles per day. If the collecting fuel reeds is similar to other norms, the daily norm was 3 bales * 5 bundles*20 manas * (mana/.4977kg) or 602.7 kilograms of reeds. The fuel equivalent per day was 602.7*16 MJ/kg or 9643 MJ per day. Reed collection was unskilled labor, so the firewood or firereed collector was probably paid 1/8 gur of barley , 5 sila of barley, or equivalent 1/8 silver piece a day. There was provision (eg. pay norms) for porters to carry the reeds to the user. A silver shekel bought 300 bundles of reeds at a weight of 20 manas per bundle or (20/.4977) 40.2 kg per bundle. In proportion, the 15 bundles of the collector should bring 15/300 or 1/20 shekel, other costs aside. There are accounts of taxes on reeds and some reed beds were noted as controlled by the royal household, priest, or princes. In energy terms, a silver shekel bought 300 bundles * 40.2 * 16 MJ/kg or 1.92E5 Megajoules. For comparison with the asphalt fuel, one shekel brought (600 manas/0.4977)*40 MJ/kg or 4.82E4 Megajoules.
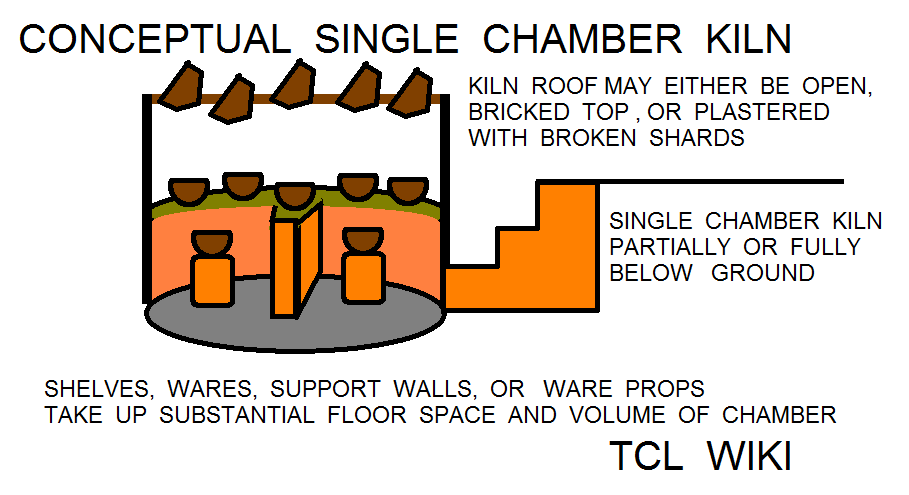
Probably the greatest improvements that the Ubaidians, Sumerians, and Greeks made was the buried combustion chamber for better insulation and the separate burning chamber and grate to force the hot air past the wares. The buried combustion chamber and separate burning chamber was rated at 7 percent efficiency over the original pit kilns (1-2%). Although difficult to interpret, some Ubaidian and Sumerian kilns had interior support walls, interior baffles, concave prism support bricks, and brick floor channels, which moderated the air flow inside the kiln (possibly efficiency of 9%, downdraft flow over the wares?). At least, the Greeks had some manual chokes or obstructions in the kiln chimney to dampen the air during preburn and moderate the air flow from the kiln exit (probably a 2 percent gain, if present). Some of the Sumerian kilns had extended or roofed stoking channels (1-2 meters long), which may have been to improve air draft at the entry and reduce wind eddies at the stoking chamber door. Some of the roofed stoking channels are sloping downwards to a below ground combustion chamber, which could be interpreted as gravity feed of fuel. Rarely, air flues of pebble beds under a raised kiln subfloor have been found at Tell Ziyada. The pebble beds in the Tell Ziyada kiln may have preheated the air and distributed air to the rear of the kiln ( 4700 BCE?, Ubaid culture). Its not uncommon on the contemporary traditional kilns to see flaming backdrafts and smoke at the stoking door, which surely indicates poor draft and a heat loss. Some of the tablets fired in Sumeria had pinholes or firing holes in the tablets, possibly for improving the evenness of fired clay. There are a number of Sumerian fired vessels and unfired vessels that were coated with pitch for waterproofing, which may have saved on fuel. Some of the traditional Indian and Mexican kilns have blackened pottery or black core pottery from added carbon or organics, but this is uncommonly reported in Sumerian pottery or difficult to interpret as an improvement. Most of the Sumerian above ground structure and kiln roofs have not survived, but some traditional Indian kilns have roofs of layered mudplaster, shards, and straw, which would serve for insulation. The use of renewable reeds for fuel probably has some lessons in the modern era. One reason for studing the Sumerian kilns is the improvement of contemporary design in that the Sumerians faced and solved many of the same problems in kiln design.
Ideal Heat budget of a circular kiln
| terms of heat budget | percent | fraction | rounded fraction in base 60 | comment or improvement |
|---|---|---|---|---|
| top kiln | 5.5 | 1/18 | 4/60 | insulation, mud plaster on top |
| bottom kiln | 5.5 | 1/18 | 4/60 | insulation, few excavation comments |
| walls kiln | 22. | 4/18 | 13/60 | insulation, mud plaster on walls |
| heat loss to chimney | 50. | 9/18 | 30/60 | use waste heat, preheat entry air |
| wares, clay mass | 16.6 | 3/18 | 10/60 | holes in bricks for maximum exposure |
| hollow core bricks, not found so far | ||||
| lead more hot air onto wares | ||||
| design wares for maximum exposure | ||||
| ware props and stands for better exposure | ||||
| design wares for least needed heat | ||||
| incorporate fuel into clay mass | ||||
| use waste heat to dry (next batch) wares and fuel | ||||
| sum of total heat | 100.0 | 18/18 | 60/60 | price tab for pottery and bricks |
Common sizes or ranges of circular kilns, burning chamber
| diameter meters | height meters | vol. cubic meters | circumference | nindans cfe | pitch vol gurs | wood kg | manas of wood | decimal workday loading | gur formula???? |
|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.5 | 0.0981 | 1.57 | 0.2616 | 0.327 | 83.385 | 167.540 | 0.0327 | 0.358 |
| 1.0 | 1.0 | 0.7853 | 3.14 | 0.523 | 2.617 | 667.505 | 1341.179 | 0.261 | 2.866 |
| 1.5 | 1.5 | 2.6507 | 4.71 | 0.785 | 8.835 | 2253.095 | 4527.014 | 0.8833 | 9.674 |
| 2. | 2. | 6.283 | 6.283 | 1.047 | 20.943 | 5340.55 | 10730.460 | 2.0933 | 22.965 |
Sumerian coefficients at the pottery factory
| daily work of one man etc. | ||||||
|---|---|---|---|---|---|---|
| in base 60 | transliterated name | english | decimal /fraction | reciprocal | comment | |
| 0:12 | sa has-as-bi | coefficient it's | 12/60 | 5 | possibly making 5 ration bowls a day , pottery | |
| 4 | sa dug bi | coefficient rate | 60/15 | 15/60 | making 4 ration bowls a day , pottery | |
| 3:45 | sa pi-ti-iq-ti | coefficient wall high | 3/60+45/3600 | 16 | raising mud wall, 3/60+45/3600 surface a day | |
| 20/60 | sa sag | coefficient making bricks | 20/60 | 60/20 | making 240 bricks a day or 20/60 sar | |
| 1:30? | igi.gub gis | coefficient wood funiture | 1+30/60 | 90/60 | 1.5 days on task, pegging planks, making door, bed or chair a day | |
| 40/60 | sa gis-ig | coefficient wood door | 40/60 | 60/40 | 2/3 door a day, planing wood and pegging planks | |
| 3 | sa gis pannum | coefficient wood crates | 3 | 20/60 | 3 crates a day, pegging planks, pannum measure crates | |
| 7:26 | sa gis | coefficient making wood plank surface | ~7/60 | ~ 60/7 | planks & crates ,daily 3crates*6sides*.497*.497= 4.44 sq.m., 4.44/36 = decimal 0.123 sar or 7/60+ 23/3600 sar daily | |
| 12 | u4, u4-1-se | hours of workday | 12 | 6/60 | common to several accounts and math problems | |
| 20:48:06 | sa gir4 ad kup4 | reed worker's kiln coefficient | ~20/60 | ~60/20 | possibly fraction for volume of combustion chamber fuel over total chamber volume | |
| 10:45:06 | esir2 had5 a sa in-na ki-ri-im | pitch in kiln coefficient | ~10/60 | ~60/10 | possibly fraction for volume of combustion chamber fuel over total chamber volume | |
| 20 | sa3 sahar ha-ba-ti | coefficient sar digging clay | 20/60 | 60/20 | 20/60 gur for clay mining (river banks?), equiv. 6 cubic meters | |
| 10 | sa3 sahar ba-la-lu | coef. sar mixing earth of one man | 10/60 | 60/10 | 3 cubic meters of clay mixing | |
| 24 | sa3 sig4 sa3-ha-a-ti | coefficient brick forming earth | 24/60 | 60/24 | another daily norm on forming brick possiby 24/60 (brick) sar= 24/60 * 720 or 288 (baked?) bricks a day | |
| 20 | sa3 sig4 | coefficient making bricks | 20/60 | 60/20 | another daily norm equals 240 bricks a day, 8*60 = 240, 20/60 * 720 =240 bricks | |
| 6_40 | sa3? im lag | coefficient making mud squares (bricks) | 6/60 +40/3600 | ~60/6 | another daily norm,decimal 0.111*720 equals 80 mud?? bricks a day, | |
| 4_16 | sa3? im lag | coefficient making mud squares (bricks) | 4/60 +16/3600 | ~60/4 | another daily norm,decimal 0.0711*720 equals 51 mud?? bricks a day, | |
| 1_41_15 | igi-gub sig4 ib2 si8 | recip. coeff. brick square mass | 0.02875 | 34.78 | recip. mass of mud? brick, decimal 0.02875 1/manas,34.78 mannas, 69.88 kg mass | |
| 3_22_30 | igi-gub sig4 in | recip. coeff. brick in xxx? | 0.0575 | 17.39 | recip. mass of mud? brick , decimal 0.0575 1/manas,17.39 mannas, 34.94 kg mass | |
| 5_24 | igi-gub pes sig4 al-ur-ra | recip. coeff. thirds brick fired | 0.09 | 11.11 | recip. mass of fired brick , decimal 0.09 1/manas,11.11 mannas, 22.32 kg mass | |
| 2_42 | igi-gub sig4 al-ur-ra | recip. coeff. brick fired | 0.045 | 22.22 | recip. mass of fired brick, decimal 0.045 1/manas,22.22 mannas, 44.64 kg mass | |
| 1_20 | igi-gub sahar il2 sig4 du3 | constant of carrying (of bricks) mud | 1/60+20/3600 | ~ 60/1 | daily task bringing mud, 1/60+20/3600 gurs,decimal 0.222 gurs,.222gurs*18.= 4 cubic meters of clay | |
| 9 | im-gir4 | mud kiln | 9 | 1/9 | 9 sar bricks, contents of an im-gir4, truncated triangular prism, possible clamp kiln, 9sar*720= 6480 bricks |
| table: Wet, Sun Dried, Fired Brick Ratios | printed in | tcl wiki format | |||
|---|---|---|---|---|---|
| ratio | alternate ratio for base60 | decimal base10 | numerator | denominator | comment, if any |
| 3/2 | 90/60 | 1.5 | wet bricks | fired bricks | Old Babylonian |
| 2/3 | 60/90 | 0.666 | fired bricks | wet bricks | Old Babylonian |
| 6/5 | 72/60 | 1.2 | sun dried brick | fired bricks | Old Babylonian |
| 5/6 | 50/60 | 0.8333 | fired brick | sun dried bricks | Old Babylonian |
| 1/1 | 60/60 | 1. | fired bricks | fired bricks | Old Babylonian |
| 5/1 | 300/60 | 5. | price of fired bricks gur/sar | price of fired bricks gur/sar | more common, Old Babylonian |
| 10/1 | 600/60 | 10. | price of fired bricks gur/sar | price of fired bricks gur/sar | less common, redundant, Old Babylonian |
| 1/5 | 12/60 | 0.20 | market rate of fired bricks sar/gur | market rate of unfired bricks sar/gur | more common , Old Babylonian |
| 1/10 | 6/60 | 0.10 | market rate of fired bricks sar/gur | market rate of unfired bricks sar/gur | less common , redundant, Old Babylonian |
| 6.3/5 | 76/60 | 1.2666 | sun dried brick | fired bricks | modern estimate in analysis here |
| O.B. derived mostly from calculations in texts, not necessarily coefficient tables | |||||
| Alternate or redundant values intended for ranging calculations , not hard and fast coefficients by themselves |
Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
Testcase 1
| kiln dimension | |||||
|---|---|---|---|---|---|
| meters or other | testcase 1 | testcase 2 | testcase 3 | testcase 4 | comment |
| diameter of combustion chamber | .5 | 1. | 1.5 | 2. | optional,many traditional kilns have single chamber |
| height of combustion chamber | .5 | 1. | 1.5 | 2. | diameter and height |
| base length central support | .25 | .25 | .4 | .5 | circular support base |
| width central support | .25 | .25 | .4 | .5 | circular support base |
| vertical height of firing chamber | .5 | 1. | 1.5 | 2. | some are single chambers |
| width of firing chamber | .5 | 1. | 1.5 | 2. | equals combustion chamber |
| height of firing chamber dome (if) | .2 | .3 | .4 | .5 | optional,many traditional kilns do not have domes or tops |
| thickness of floor on f. chamber | .07 | .07 | .1 | .1 | optional,many traditional kilns do not have brick floors |
| length of stoking channel | .75 | .75 | .75 | .8 | should be small or closeable |
| width of stoking channel | .25 | .30 | .40 | .4 | should be small or closeable |
| chimney height | 6 | 9 | 12 | 15 | many traditional kilns do not have chimneys |
| air valve, chimney damper | .25 | .25 | .25 | .25 | advanced feature, not usually on traditional kilns |
Testcase 4
| quantity | value | units |
|---|---|---|
| wood kiln is fired for | 5 | days |
| fuel | 1 | cord wood a day. |
| firing temperature | 1200 | degrees centigrade. |
| combustion chamber | 4 | cubic meters |
Testcase 5
| quantity | value | units | comment |
|---|---|---|---|
| wood kiln is fired for | 5 | hours | |
| diameter of combustion chamber | 2 | meters | |
| internal diameter of c. chamber | 1.7 | meters | |
| height of combustion chamber | 1.5 | meters | |
| fuel | 400 | kilograms wood a day. | |
| ambient temperature | 30 | centigrade. | |
| firing temperature | 1000 | degrees centigrade | . |
| combustion chamber | 4 | cubic meters | |
| chimney height | 6 | meters | |
| white oak | 3700 | lb/cord | |
| white oak | 24 | MMBTU/cord | |
| white oak specific gravity | 850 | kilograms per cubic meter |
One MMBtu = 1,000,000 Btu mass_flow_rate = burning_area* fuel_burn_rate*fuel_density where fuel_burn_rate= initial_rate + (e**+c*kelvin)
Testcase 6
testcase number: 6 max room fuel kg 2705.181 estimated fuel,oak kg 369.708 total heat megajoules 4991.059 kiln style single chamber, circular
| testcase number: 6 | |||
|---|---|---|---|
| calculator inputs | known values | comment | |
| kiln diameter meters | 1.83 | inner diameter | |
| kiln height meters | 1.21 | really single chamber kiln | |
| volume cubic meters | 3.18 | ||
| kiln firing seconds | 8100 | ||
| outputs | < | < | < |
| calculator outputs | calc. value | measured | comment |
| estimated fuel,oak kg | 369.708 | 350 kg | calculator based on oak |
| total heat megajoules | 4991.05 | 4971.0 | very close match |
| firing max temperature | 750 | 660 | accuracy very sensitive to firing time |
| man workdays to load fuel | 1.060 | est., not reported |
test of offsite image retrival
Screenshots Section
figure 1.
figure 1b.
figure 2.
figure 3.
figure 4.
figure 5.
figure 6.
figure 7.
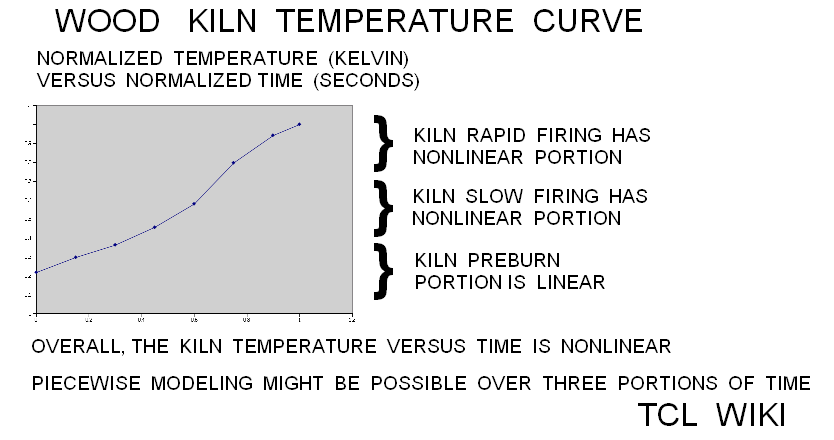
figure 8.
figure 9.
figure 10.
figure 11.
References:
- Kenyan Ceramic Jiko cooking stove, by Hugh Allen
- DELCROIX, G. et HUOT, J.L., 1972, « Les fours dits « de potier » dans l’Orient ancien
- Michio: Anagama: Building Kilns and Firing
- Saraswati, B. and N.B. Behura. 1966. Pottery Techniques of Peasant India.
- Traditional Potters of India, [L1 ]
- Planting and Growing Miscanthus Reed [L2 ]
- Brick and Ceramic Sectors [L3 ]
- Energy Measurements and Conversions [L4 ]
- Mani Kiln (google >> mani kiln efficient)
- Village-Level Brickmaking [L5 ]
- Technical problems of brick production, prepared by Kelvin Mason (June 1998) [L6 ]
- Energy Used to Fire Clay Bricks, prepared by Kelvin Mason, June1998 [L7 ]
- Energy Used ... good simple math for bricks, much used [L8 ]
- Building the Mani Kiln, Drawings by Manny Hernandez (google >> mani kiln efficient)
- Ten Rules for Brick Firing,prepared by Theo Schilderman (June 1998) [L9 ]
- CFD Simulation of Flue Gas Flow in Traditional Pottery , Cecilia Schotte, thesis
- CFD Simulation of Flue Gas Flow in Pottery Furnace, Kristina Nilenius, thesis
- Equivalency values of the UR III period, Robert K. Englund, CDLI Library[L10 ]
- Equivalency values page & CDLI MySQL search engine , CDLI Library [L11 ]
Appendix Code
appendix TCL programs and scripts
# TCL source code follows
# pretty print from autoindent and ased editor
# Sumerian Circular Kiln calculator V2
# written on Windows XP on TCL
# working under TCL version 8.6
# gold on TCL Club, 12Dec2018
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {kiln diameter meters:} }
lappend names {burning chamber height:}
lappend names {firing time seconds: }
lappend names {answer: volume cubic meters: }
lappend names {total heat units, megajoules:}
lappend names {optional: }
lappend names {optional: }
lappend names {firing max temperature centigrade: }
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Sumerian Circular Kiln
from TCL
# gold on TCL Club, 12Dec2018 "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg " Rectangular Radio Antenna V2
from TCL ,
# self help listing
# problem, Sumerian Circular Kiln V2
# 1 given follows.
1) frequency megahertz:
# Recommended procedure is push testcase and fill frame,
# change first three entries etc, push solve,
# and then push report. Report allows copy and paste
# from console to conventional texteditor. For testcases
# testcase number is internal to the calculator and
# will not be printed until the report button is pushed
# for the current result numbers.
# >>> copyright notice <<<
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK license terms.
# Editorial rights and disclaimers
# retained under the TCL/TK license terms
# and will be defended as necessary in court.
Conventional text editor formulas or grabbed from internet
screens can be pasted into green console.
# gold on TCL Club, 12Dec2018 "
tk_messageBox -title "Self_Help" -message $msg }
proc pi {} {expr acos(-1)}
proc kilnvolumex { d h } {
set kilnvolumexxx [* .25 [pi] $d $d $h ]
return $kilnvolumexxx
}
proc heatx { vol density } {
set fuel_mass [* $vol $density]
set total_heat [* $fuel_mass 13.54]
return $total_heat
}
proc firingtempxx { total_heat burn_time cross_section temp_ambient temp_flame} {
set d $cross_section
set firing_temp 1
set heat_flux [/ $total_heat $burn_time]
set heat_flux_persec [/ $heat_flux $burn_time]
set cross_section [ / [* [pi] $d $d ] 4.]
set item 25
set temp_ambient 25
set temp_flame 1488.
set tx $temp_ambient
set taxx $temp_flame
set t 25
set h [/ $heat_flux_persec $cross_section]
while {$item <= 4000} {
incr item
set t [+ $t 1 ]
set term1 [* 1. $t $t $t $t]
set term2 [* 1. $tx $tx $tx $tx]
set term1 [* .000000000056703 [ - $term1 $term2]]
set term2 [* $h 1.1 [/ [- $taxx $t] [ - $taxx $tx ]]]
set difference [abs [- $term1 $term2]]
if {$difference < 2.} { set temp_answer $t }
}
return $temp_answer
}
proc calculate { } {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
global kiln_volume kiln_temperature_exp
global workdays total_heat massfromvolume
global total_heat firing_temp fuel
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set kiln_diameter $side1
set kiln_height $side2
set kiln_firing_time $side3
set ktime $side3
set kiln_volume 1
set kiln_volume [kilnvolumex $kiln_diameter $kiln_height]
set fuel_density 850
set massfromvolume [* $kiln_volume $fuel_density]
set fuel [* [ / 8.2 60. ] $massfromvolume]
set total_heat [* 13.5 $fuel]
set kiln_temperature_exp [+ 300. [ exp [* 1. .001 $ktime]]]
set temp_amb 25.
set temp_flame 1488.
set total_heat_joules [* $total_heat 1.0E6]
set firing_temp [firingtempxx $total_heat_joules $kiln_firing_time $kiln_diameter $temp_amb $temp_flame]
# possible type change error in original, 900. ?=>? 900
# following clamp kiln temp to 900.
if { $kiln_temperature_exp > 900. } { set kiln_temperature_exp 900. }
set workdays [/ $kiln_volume 3. ]
set side4 $kiln_volume
set side5 $total_heat
set side8 $firing_temp
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
global wavelength wavelength2
global wavelength6 wavelength10
global wavelengthsq surfacearea
global megafrequency
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Sumerian Circular Kiln Report V2, screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
console show;
puts "%|table $testcase_number |printed in| tcl format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number :|testcase_number | |&"
puts "&| $side1 :|kiln diameter meters: | |&"
puts "&| $side2 :|burning chamber height: | |& "
puts "&| $side3 :|firing time seconds: | |& "
puts "&| $side4 :|answer: volume cubic meters | |&"
puts "&| $side5 :|total heat units, megajoules: | |&"
puts "&| $side6 :|optional: | |&"
puts "&| $side7 :|optional: | |&"
puts "&| $side8 :|firing max temperature centigrade: | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup .5 .5 6000. 0.0981 153.9 0. 0. 700. }
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 1.5 1.5 6000. 2.65 4156. 0. 0. 870. }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 2. 2. 6000. 6.28 9853. 0. 0. 900. }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .self_help -text self_help -command { self_help }
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Sumerian Circular Kiln Calculator V2"
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console. While the testcases are in meters, the units either cancel out or are carried through in the calculator equations. So the units could be entered as English feet, Egyptian royal cubits, Sumerian gars, or Chinese inches and the outputs of volume will in the same (cubic) units. This is an advantage since the units in the ancient Sumerian, Indian, and Chinese texts are open to question. In some benign quarters of the globe, feet and cubic feet were still being used for design in the 1970's.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers (which numbers will be cleared on the next solve button.) The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
initial console program
# pretty print from autoindent and ased editor
# volume of Sumerian kiln combustion chamber
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI , 24jul2013
package require Tk
namespace path {::tcl::mathop ::tcl::mathfunc}
console show
set diameter .5
set height .5
set kiln_volume [ * .25 3.14 $diameter $diameter $height]
set kiln_volume_gurs [ / $kiln_volume .3 ]
set workdays [ / [* $kiln_volume_gurs 60] 10 ]
puts "kiln_volume $kiln_volume"
puts "kiln_volume_gurs $kiln_volume_gurs"
puts "man workdays $workdays"Comments Section
Please place any comments here with your wiki MONIKER and date, Thanks, gold 12DEC2018
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |