Tension Splines
2003-12-08 - new page
2003-12-17 - added bezier curves

I needed some spline with tension tcl code. I hacked Keith Vetter's Cubic Splines GUI and added some tension algorithms. The reference where each algorithm came from is listed in the code.
Enjoy!
BAJ You can run this code via Jacl/Swank/Java Web Start at http://www.onemoonscientific.com/swank/tensionspline.jnlp
# the next line restarts using wish \
exec wish "$0" "$@" -visual truecolor
## Cubic Tension Splines: TensionSpline.tcl
###############################################################################################
## Greg Blair 2003-09-29 ##
## I took Keith Vetters Cubic Spline code and added TC and TCB tension, cardinal, ##
## Catmull Rom splines as well as linear and cosine interpolation ##
## using C code I found at: ##
## ##
## http://astronomy.swin.edu.au/~pbourke/analysis/interpolation/ and ##
## http://www.cubic.org/~submissive/sourcerer/hermite.htm ##
## ##
## I hand converted the c code to TCL, and extended Keith's test GUI for the new curve types ##
## ##
## I have include the comments from the websites as documentation to the methods implemented ##
###############################################################################################
##Keith Vetter 2003-03-07 - one feature often noted as missing from tk the ability of the canvas to do cubic splines.
##Here is a routine PolyLine::CubicSpline that takes a list of (x,y) values of control points and returns a
## list points on the cubic spline curve that's suitable to be used by: canvas create line [PolyLine::CubicSplint $xy] ...
##+##########################################################################
#
# CubicSpline -- routines to generate the coordinates of a cubic spline
# given a list of control points. Also included is demo/test harness
# by Keith Vetter
#
# Revisions:
# KPV Mar 07, 2003 - initial revision
#
namespace eval Cubic {}
namespace eval PolyLine {}
##+##########################################################################
#
# CubicSpline - returns the x,y coordinates of the cubic spline using
# xy control points.
# xy => {{x0 y0} {x1 y1} .... {xn yn}}
#
# XY points MUST BE SORTED by increasing x
#
proc PolyLine::CubicSpline {xy {PRECISION 10}} {
set np [expr {[llength $xy] / 2}]
if {$np <= 1} return
set idx 0
foreach {x y} $xy {
set X($idx) $x
set Y($idx) $y
incr idx
}
for {set i 1; set last $X(0)} {$i < $np} {set last $X($i); incr i} {
set h($i) [expr {double($X($i) - $last)}]
if {$h($i) == 0} return
if {$h($i) < 0} return ;# ERROR not sorted
}
if {$np > 2} {
for {set i 1} {$i < $np-1} {incr i} {
set i2 [expr {$i + 1}]
set i0 [expr {$i - 1}]
set diag($i) [expr {($h($i) + $h($i2))/3.0}]
set sup($i) [expr {$h($i2) / 6.0}]
set sub($i) [expr {$h($i) / 6.0}]
set a($i) [expr {($Y($i2) - $Y($i))/$h($i2) -
($Y($i) - $Y($i0)) / $h($i)}]
}
PolyLine::SolveTridiag sub diag sup a [expr {$np - 2}]
}
set a(0) [set a([expr {$np - 1}]) 0]
# Now generate the point list
set xy [list $X(0) $Y(0)]
for {set i 1} {$i < $np} {incr i} {
set i0 [expr {$i - 1}]
for {set j 1} {$j <= $PRECISION} {incr j} {
set t1 [expr {($h($i) * $j) / $PRECISION}]
set t2 [expr {$h($i) - $t1}]
set y [expr {((-$a($i0)/6 * ($t2 + $h($i)) * $t1 +
$Y($i0))* $t2 + (-$a($i)/6 *
($t1+$h($i)) * $t2 + $Y($i)) * $t1)/$h($i)}]
set t [expr {$X($i0) + $t1}]
lappend xy $t $y
}
}
return $xy
}
##+##########################################################################
# SolveTriDiag -- solves the linear system for tridiagoal NxN matrix A
# using Gaussian elimination (no pivoting). Since A is sparse, we pass
# in three diagonals:
# sub(i) => a(i,i-1) diag(i) => a(i,i) sup(i) => a(i,i+1)
#
# Result is returned in b[1:n]
#
proc PolyLine::SolveTridiag {N_sub N_diag N_sup N_b n} {
upvar 1 $N_sub sub
upvar 1 $N_diag diag
upvar 1 $N_sup sup
upvar 1 $N_b b
# Factorization and forward substitution
for {set i 2} {$i <= $n} {incr i} {
set i0 [expr {$i - 1}]
set sub($i) [expr {$sub($i) / $diag($i0)}]
set diag($i) [expr {$diag($i) - $sub($i) * $sup($i0)}]
set b($i) [expr {$b($i) - $sub($i) * $b($i0)}]
}
set b($n) [expr {$b($n) / $diag($n)}]
for {set i [expr {$n - 1}]} {$i >= 1} {incr i -1} {
set i2 [expr {$i + 1}]
set b($i) [expr {($b($i) - $sup($i) * $b($i2)) / $diag($i)}]
}
}
#########################################################################
## from: http://astronomy.swin.edu.au/~pbourke/analysis/interpolation/ ##
#########################################################################
## Discussed here are a number of interpolation methods, this is by no
## means an exhaustive list but the methods shown tend to be those in
## common use in computer graphics. The main attributes is that they
## are easy to compute and are stable. Interpolation as used here is
## different to "smoothing", the techniques discussed here have the
## characteristic that the estimated curve passes through all the
## given points. The idea is that the points are in some sense correct
## and lie on an underlying but unknown curve, the problem is to be
## able to estimate the values of the curve at any position between
## the known points.
## Linear interpolation is the simplest method of getting values at
## positions in between the data points. The points are simply joined
## by straight line segments. Each segment (bounded by two data points)
## can be interpolated independently. The parameter mu defines where
## to estimate the value on the interpolated line, it is 0 at the
## first point and 1 and the second point. For interpolated values
## between the two points mu ranges between 0 and 1. Values of mu
## outside this range result in extrapolation. This convention is
## followed for all the subsequent methods below. As with subsequent
## more interesting methods, a snippet of plain C code will server
## to describe the mathematics.
proc LinearInterpolate {y1 y2 mu} {
# http://astronomy.swin.edu.au/~pbourke/analysis/interpolation/
## return [expr {$y1*(1-$mu)+$y2*$mu}] ;# 2 multiplies 1 add, 1 subtract
return [expr {$y1+$mu*($y2-$y1)}] ;# 1 multiply 1 add, 1 subtract
}
## Linear interpolation results in discontinuities at each point.
## Often a smoother interpolating function is desirable, perhaps
## the simplest is cosine interpolation. A suitable orientated
## piece of a cosine function serves to provide a smooth transition
## between adjacent segments.
proc CosineInterpolate {y1 y2 mu} {
# http://astronomy.swin.edu.au/~pbourke/analysis/interpolation/
## Paul Burke, on his website does mentions:
## By a cute trick the cosine interpolation reverts to linear
## if applied independently to each coordinate.
## must linear interpolate in x coord, cosine interp in y coord
set mu2 [expr {(1.-cos(3.14159265358979323846*$mu))/2.}]
## return [expr {$y1*(1.-$mu2)+$y2*$mu2}]
return [expr {$y1+$mu2*($y2-$y1)}]
}
## Cubic interpolation is the simplest method that offers true
## continuity between the segments. As such it requires more
## than just the two endpoints of the segment but also the two
## points on either side of them. So the function requires 4
## points in all labeled y0, y1, y2, and y3, in the code below.
## mu still behaves the same way for interpolating between
## the segment y1 to y2. This does raise issues for how to
## interpolate between the first and last segments. In the
## examples here I just haven't bothered. A common solution
## is the dream up two extra points at the start and end of
## the sequence, the new points are created so that they
## have a slope equal to the slope of the start or end segment.
proc CubicInterpolate {y0 y1 y2 y3 mu} {
# http://astronomy.swin.edu.au/~pbourke/analysis/interpolation/
set mu2 [expr {$mu*$mu}]
set a0 [expr {$y3 - $y2 - $y0 + $y1}]
set a1 [expr {$y0 - $y1 - $a0}]
set a2 [expr {$y2 - $y0}]
set a3 $y1
return [expr {$a0*$mu*$mu2+$a1*$mu2+$a2*$mu+$a3}]
}
## Hermite interpolation like cubic requires 4 points so that
## it can achieve a higher degree of continuity. In addition
## it has nice tension and biasing controls. Tension can be
## used to tighten up the curvature at the known points. The
## bias is used to twist the curve about the known points.
## The examples shown here have the default tension and
## bias values of 0, it will be left as an exercise for
## the reader to explore different tension and bias values.
##
## Tension: 1 is high, 0 normal, -1 is low
## Bias: 0 is even,
## positive is towards first segment,
## negative towards the other
proc HermiteInterpolate {y0 y1 y2 y3 mu tension bias} {
# http://astronomy.swin.edu.au/~pbourke/analysis/interpolation/
## GB this is a Kochanek-Bartels Spline
## (also called TCB-Splines, for tension,continuity,bias)
## GB with continuity c set to zero
## GB note variables m0,m1 are the slopes at y1,y2
set mu2 [expr {$mu * $mu}]
set mu3 [expr {$mu2 * $mu}]
set m0 [expr {($y1-$y0)*(1+$bias)*(1-$tension)/2 +
($y2-$y1)*(1-$bias)*(1-$tension)/2}]
set m1 [expr {($y2-$y1)*(1+$bias)*(1-$tension)/2 +
($y3-$y2)*(1-$bias)*(1-$tension)/2}]
set a0 [expr { 2*$mu3 - 3*$mu2 + 1}]
set a1 [expr { $mu3 - 2*$mu2 + $mu}]
set a2 [expr { $mu3 - $mu2}]
set a3 [expr {-2*$mu3 + 3*$mu2}]
return [expr {$a0*$y1+$a1*$m0+$a2*$m1+$a3*$y2}]
}
## While you may think the above cases were 2 dimensional,
## they are just 1 dimensional interpolation (the horizontal
## axis is linear). In most cases the interpolation can be
## extended into higher dimensions simply by applying it to
## each of the x,y,z coordinates independently. This is
## shown on the right for 3 dimensions for all but the
## cosine interpolation. By a cute trick the cosine
## interpolation reverts to linear if applied independently
## to each coordinate.
proc HermiteSpline {P1 P2 T1 T2 s} {
# http://www.cubic.org/~submissive/sourcerer/hermite.htm
# Vector S: The interpolation-point and it's powers up to 3:
# Vector C: The parameters of our hermite curve:
# Matrix h: The matrix form of the 4 hermite polynomials:
# S = | s^3 s^2 s 1 | | 2 -2 1 1 | | P1 |
# h = | -3 3 -2 -1 | C = | P2 |
# | 0 0 1 0 | | T1 |
# | 1 0 0 0 | | T2 |
# To calculate a point on the curve you build the Vector S,
# multiply it with the matrix h and then multiply with C.
# P = S * h * C
if {[info exist HermiteCache($s,h1)]} {
set h1 $HermiteCache($s,h1)
set h2 $HermiteCache($s,h2)
set h3 $HermiteCache($s,h3)
set h4 $HermiteCache($s,h4)
} else {
set s2 [expr {$s*$s}]
set s3 [expr {$s*$s2}]
set h1 [expr { 2.*$s3 - 3.*$s2 + 1.}]
set h2 [expr {-2.*$s3 + 3.*$s2}]
set h3 [expr { $s3 - 2.*$s2+$s}]
set h4 [expr { $s3 - $s2}]
set HermiteCache($s,h1) $h1
set HermiteCache($s,h2) $h2
set HermiteCache($s,h3) $h3
set HermiteCache($s,h4) $h4
}
return [expr {$h1*$P1 + $h2 *$P2 + $h3* $T1 + $h4*$T2}]
}
proc CardinalSpline {P0 P1 P2 P3 a s} {
# http://www.cubic.org/~submissive/sourcerer/hermite.htm
# Cardinal splines are just a subset of the hermite curves.
# They don't need the tangent points because they will be calculated from
# the control points. We'll lose some of the flexibility of the hermite
# curves, but as a tradeoff the curves will be much easier to use.
# The formula for the tangents for cardinal splines is:
# T = a * ( P - P )
# i i+1 i-1
# a is a constant which affects the tightness of the curve
# (a should be between 0 and 1, but this is not a must)
set T1 [expr {$a*($P2-$P0)}]
set T2 [expr {$a*($P3-$P1)}]
return [HermiteSpline $P1 $P2 $T1 $T2 $s]
}
proc CatmullRomSpline {P0 P1 P2 P3 s} {
# http://www.cubic.org/~submissive/sourcerer/hermite.htm
# The Catmull-Rom spline is again just a subset of the cardinal splines.
# You only have to define a as 0.5, and you can draw and interpolate
# Catmull-Rom splines.
#
# T = 0.5 * ( P - P )
# i i+1 i-1
return [CardinalSpline $P0 $P1 $P2 $P3 0.5 $s]
}
proc Lerp {a b mu} {
# -------------------------------------------------
# http://www.cubic.org/~submissive/sourcerer/bezier.htm
# simple linear interpolation between two points
# -------------------------------------------------
set ax [lindex $a 0]
set ay [lindex $a 1]
set bx [lindex $b 0]
set by [lindex $b 1]
return [list [expr {$ax + ($bx-$ax)*$mu}] [expr {$ay + ($by-$ay)*$mu}] ]
}
proc BezierSpline {a b c d mu} {
# --------------------------------------------------------
# http://www.cubic.org/~submissive/sourcerer/bezier.htm
# evaluate a point on a bezier-curve. mu goes from 0 to 1.0
# --------------------------------------------------------
set ab [Lerp $a $b $mu]
set bc [Lerp $b $c $mu]
set cd [Lerp $c $d $mu]
set abbc [Lerp $ab $bc $mu]
set bccd [Lerp $bc $cd $mu]
return [Lerp $abbc $bccd $mu]
}
proc HornerBezier {degree xc yc t} {
upvar 1 $xc xcoeff
upvar 1 $yc ycoeff
# -------------------------------------------------------------------------
# Greg Blair, algorithm derived from:
# hornbez(degree, coeff, t)
# Curves and Surface for Computer Aided Geometric Design, A Practical Guide
# Farin, Gerald, Academic Press, 2nd Edition, 1990, page 48
# -------------------------------------------------------------------------
## uses Horner's scheme to compute one coordinate
## value of a Bezier curve. Has to be called
## for each coordinate (x,y, and/or z) of a control polygon.
## Input: degree: degree of curve.
## coeff: array with coefficients of curve.
## t: parameter value.
## Output: coordinate value.
set t1 [expr {1.0 - $t}]
set fact 1.0
set n_choose_i 1
set x [expr {$xcoeff(0)*$t1}]
set y [expr {$ycoeff(0)*$t1}]
for {set i 1} {$i < $degree} {incr i} {
set fact [expr {$fact*$t}]
set n_choose_i [expr {$n_choose_i*($degree-$i+1)/$i}] ;# always int!
set x [expr {$x + $fact*$n_choose_i*$xcoeff($i)*$t1}]
set y [expr {$y + $fact*$n_choose_i*$ycoeff($i)*$t1}]
}
set x [expr {$x + $fact*$t*$xcoeff($degree)}]
set y [expr {$y + $fact*$t*$ycoeff($degree)}]
return [list $x $y]
}
proc TCBSpline {P0 P1 P2 P3 s t c b} {
# http://www.cubic.org/~submissive/sourcerer/hermite.htm
##################################################################
## note by Greg Blair: ##
## ##
## TCB splines due to Doris Kochanek, a UofWaterloo MSc student ##
## ##
## These TCB spline equations can also be found on page 433 of ##
## Splines for use in Computer Graphics & Geometric Modelling ##
## Bartels, Beatty, Barsky, Morgan Kaufman, 1987 ##
##################################################################
# The Kochanek-Bartels Splines
# (also called TCB-Splines, for tension,continuity,bias)
# Now we're going down to the guts of curve interpolation:
# The kb-splines (mostly known from Autodesk's 3d-Studio Max and Newtek's Lightwave)
# are nothing more than hermite curves and a handfull of formulas to calculate the tangents.
# These curves have been introduced by D. Kochanek and R. Bartels in 1984 to
# give animators more control over keyframe animation.
# They introduced three control-values for each keyframe point:
# Tension: How sharply does the curve bend?
# Continuity: How rapid is the change in speed and direction?
# Bias: What is the direction of the curve as it passes through the keypoint?
# I won't try to derive the tangent-formulas here. I think just giving you something you can use
# is a better idea. (if you're interested you can ask me. I can write it down and send it to you
# via email.)
# The "incoming" Tangent equation:
# (1-t)*(1-c)*(1+b)
# TS = ----------------- * ( P - P )
# i 2 i i-1
# (1-t)*(1+c)*(1-b)
# + ----------------- * ( P - P )
# 2 i+1 i
# The "outgoing" Tangent equation:
# (1-t)*(1+c)*(1+b)
# TD = ----------------- * ( P - P )
# i 2 i i-1
# (1-t)*(1-c)*(1-b)
# + ----------------- * ( P - P )
# 2 i+1 i
# When you want to interpolate the curve you should use this vector:
# | P(i) |
# C = | P(i+1) |
# | TD(i) |
# | TS(i+1) |
# You might notice that you always need the previous and next point
# if you want to calculate the curve. This might be a problem when you try
# to calculate keyframe data from Lightwave or 3D-Studio. I don't
# know exactly how these programs handle the cases of the first and last point, but
# there are enough sources available on the internet. Just search around
# a little bit. (Newtek has a good developer section. You can download
# the origignal Lightwave motion code on their web-site).
set TD1 [expr {(1.-$t)*(1.-$c)*(1.+$b)/2*($P1 - $P0)
+ (1.-$t)*(1.+$c)*(1.-$b)/2*($P2 - $P1)}]
set TS2 [expr {(1.-$t)*(1.+$c)*(1.+$b)/2*($P2 - $P1)
+ (1.-$t)*(1.-$c)*(1.-$b)/2*($P3 - $P2)}]
return [HermiteSpline $P1 $P2 $TD1 $TS2 $s]
}
proc KeyFrameTCBSpline {P0 P1 P2 P3 s t c b N0 N1 N2} {
# http://www.cubic.org/~submissive/sourcerer/hermite.htm
# Speed Control
# If you write yourself keyframe-interpolation code and put it into a program
# you'll notice one problem:
# Unless you have your keyframes in fixed intervals you will have a sudden change
# of speed and direction whenever you pass a keyframe-point.
# This can be avoided if you take the number of key-positions (frames) between two keyframes into account:
# N is the number of frames (seconds, whatever) between two keypoints.
# 2 * N
# i-1
# TD = TD * --------------- adjustment of outgoing tangent
# i i N + N
# i-1 i
# 2 * N
# i
# TS = TS * --------------- adjustment of incomming tangent
# i i N + N
# i-1 i
set TD1 [expr {(1.-$t)*(1.-$c)*(1.+$b)/2*($P1 - $P0)
+ (1.-$t)*(1.+$c)*(1.-$b)/2*($P2 - $P1)}]
set TS2 [expr {(1.-$t)*(1.+$c)*(1.+$b)/2*($P2 - $P1)
+ (1.-$t)*(1.-$c)*(1.-$b)/2*($P3 - $P2)}]
set D [expr {$N0 + $N1}]
if {$D} {
set TD1 [expr {$TD1 * 2.*$N0/$D}]
}
set D [expr {$N1+$N2}]
if {$D} {
set TS2 [expr {$TS2 * 2.*$N2/$D}]
}
return [HermiteSpline $P1 $P2 $TD1 $TS2 $s]
}
proc PolyLine::Linear {xy {PRECISION 10}} {
set np [expr {[llength $xy] / 2}]
if {$np <= 1} return
set idx 0
foreach {x y} $xy {
set X($idx) $x
set Y($idx) $y
incr idx
}
# Now generate the point list
set xy [list $X(0) $Y(0)]
for {set i 1} {$i < $np} {incr i} {
set i0 [expr {$i - 1}]
for {set j 0} {$j <= $PRECISION} {incr j} {
set mu [expr {double($j) / double($PRECISION)}]
set x [LinearInterpolate $X($i0) $X($i) $mu]
set y [LinearInterpolate $Y($i0) $Y($i) $mu]
lappend xy $x $y
}
}
return $xy
}
proc PolyLine::Cosine {xy {PRECISION 10}} {
set np [expr {[llength $xy] / 2}]
if {$np <= 1} return
set idx 0
foreach {x y} $xy {
set X($idx) $x
set Y($idx) $y
incr idx
}
# Now generate the point list
set xy [list $X(0) $Y(0)]
for {set i 1} {$i < $np} {incr i} {
set i0 [expr {$i - 1}]
for {set j 0} {$j <= $PRECISION} {incr j} {
set mu [expr {double($j) / double($PRECISION)}]
## Paul Burke, on the website does mention:
## By a cute trick the cosine interpolation reverts to linear
## if applied independently to each coordinate.
## Now
set x [CosineInterpolate $X($i0) $X($i) $mu]
## does generate linear interpolation
## linear interpolation on x and cosine interpolation on y
set x [LinearInterpolate $X($i0) $X($i) $mu]
set y [CosineInterpolate $Y($i0) $Y($i) $mu]
lappend xy $x $y
}
}
return $xy
}
proc PolyLine::CatmullRom {xy {PRECISION 10}} {
set np [expr {[llength $xy] / 2}]
if {$np <= 1} return
set idx 0
foreach {x y} $xy {
set X($idx) $x
set Y($idx) $y
incr idx
if {$idx == 1} {
set X($idx) $x
set Y($idx) $y
incr idx
}
}
## duplicate last point
set X($idx) $x
set Y($idx) $y
incr idx
# Now generate the point list
set xy [list $X(0) $Y(0)]
for {set i 1} {$i < $np} {incr i} {
set i0 [expr {$i - 1}]
set i2 [expr {$i + 1}]
set i3 [expr {$i + 2}]
for {set j 0} {$j <= $PRECISION} {incr j} {
set mu [expr {double($j) / double($PRECISION)}]
set x [CatmullRomSpline $X($i0) $X($i) $X($i2) $X($i3) $mu]
set y [CatmullRomSpline $Y($i0) $Y($i) $Y($i2) $Y($i3) $mu]
lappend xy $x $y
}
}
return $xy
}
proc PolyLine::Bezier {xy {PRECISION 10}} {
set np [expr {[llength $xy] / 2}]
if {$np < 4} return
set idx 0
foreach {x y} $xy {
set X($idx) $x
set Y($idx) $y
incr idx
}
set xy {}
set idx 0
while {[expr {$idx+4}] <= $np} {
set a [list $X($idx) $Y($idx)]; incr idx
set b [list $X($idx) $Y($idx)]; incr idx
set c [list $X($idx) $Y($idx)]; incr idx
set d [list $X($idx) $Y($idx)];# incr idx ;# use last pt as 1st pt of next segment
for {set j 0} {$j <= $PRECISION} {incr j} {
set mu [expr {double($j) / double($PRECISION)}]
set pt [BezierSpline $a $b $c $d $mu]
lappend xy [lindex $pt 0] [lindex $pt 1]
}
}
return $xy
}
proc PolyLine::FDBezier {xy {PRECISION 10}} { ;# forward differencing Bezier calc.
## http://www.niksula.cs.hut.fi/~hkankaan/Homepages/bezierfast.html
## Calculating bezier curves is quite processor intensive task, but
## this algorithm will make calculating at least 10 times faster.
## Especially with bezier surfaces of bezier spaces, you will need the speed.
## All polynomial functions can be calculated via forward differencing.
## The key idea is to start at some point of the function, move forwards
## at constant step and use Taylor series to calculate the next value.
## Further reading
## The algo I presented here may not be the best one, but it works fine
## for most 3d applications. If you need more, read these:
## Adaptive forward differencing for rendering curves and surfaces;
## Sheue-Ling Lien, Michael Shantz and Vaughan Pratt;
## Proceedings of the 14th annual conference on Computer graphics, 1987, Pages 111 - 118
## Rendering trimmed NURBS with adaptive forward differencing;
## M. Shantz and Sheue-Ling Chang;
## Proceedings of the 15th annual conference on Computer graphics, 1988, Pages 189 - 198
## Rendering cubic curves and surfaces with integer adaptive forward differencing;
## S.-L. Chang and M. S. R. Rocchetti;
## Conference proceedings on Computer graphics, 1989, Pages 157 - 166
set np [expr {[llength $xy] / 2}]
if {$np < 4} return
set idx 0
foreach {x y} $xy {
set X($idx) $x
set Y($idx) $y
incr idx
}
set t [expr {1.0 / double($PRECISION)}]
set temp [expr { $t * $t}]
set idx 0
set xy {}
while {[expr {$idx+4}] <= $np} { ;# segment loop
set X0 $X($idx)
set Y0 $Y($idx); incr idx
set X1 $X($idx)
set Y1 $Y($idx); incr idx
set X2 $X($idx)
set Y2 $Y($idx); incr idx
set X3 $X($idx)
set Y3 $Y($idx);# re-use last pt for 1st pt of next segment
set xf $X0
set yf $Y0
set xfd [expr { 3 * ($X1 - $X0) * $t}]
set yfd [expr { 3 * ($Y1 - $Y0) * $t}]
set xfdd_per_2 [expr { 3 * ($X0 - 2 * $X1 + $X2) * $temp}]
set yfdd_per_2 [expr { 3 * ($Y0 - 2 * $Y1 + $Y2) * $temp}]
set xfddd_per_2 [expr { 3 * (3 * ($X1 - $X2) + $X3 - $X0) * $temp * $t}]
set yfddd_per_2 [expr { 3 * (3 * ($Y1 - $Y2) + $Y3 - $Y0) * $temp * $t}]
set xfddd [expr { $xfddd_per_2 + $xfddd_per_2}]
set yfddd [expr { $yfddd_per_2 + $yfddd_per_2}]
set xfdd [expr { $xfdd_per_2 + $xfdd_per_2}]
set yfdd [expr { $yfdd_per_2 + $yfdd_per_2}]
set xfddd_per_6 [expr { $xfddd_per_2 * (1.0 / 3)}]
set yfddd_per_6 [expr { $yfddd_per_2 * (1.0 / 3)}]
for {set j $PRECISION} {$j} {incr j -1} { ;# pt in segment loop
lappend xy $xf $yf
set xf [expr { $xf + $xfd + $xfdd_per_2 + $xfddd_per_6}]
set yf [expr { $yf + $yfd + $yfdd_per_2 + $yfddd_per_6}]
set xfd [expr { $xfd + $xfdd + $xfddd_per_2}]
set yfd [expr { $yfd + $yfdd + $yfddd_per_2}]
set xfdd [expr { $xfdd + $xfddd}]
set yfdd [expr { $yfdd + $yfddd}]
set xfdd_per_2 [expr { $xfdd_per_2 + $xfddd_per_2}]
set yfdd_per_2 [expr { $yfdd_per_2 + $yfddd_per_2}]
}
}
lappend xy $X3 $Y3
return $xy
}
proc PolyLine::HornBezier {xy {PRECISION 10}} {
set np [expr {[llength $xy] / 2}]
if {$np < 3} return
set idx 0
foreach {x y} $xy {
set X($idx) $x
set Y($idx) $y
incr idx
}
set degree [expr { $np -1 }]
# Now generate the point list
# 1st knot
set xy [list $X(0) $Y(0)]
# interpolate for intermediate points
for {set j 1} {$j < $PRECISION} {incr j} {
set t [expr {double($j) / double($PRECISION)}]
set pt [HornerBezier $degree X Y $t]
lappend xy [lindex $pt 0] [lindex $pt 1]
}
# 2nd knot
lappend xy $X($degree) $Y($degree)
return $xy
}
proc PolyLine::Cardinal {xy a {PRECISION 10}} {
set np [expr {[llength $xy] / 2}]
if {$np <= 1} return
set idx 0
foreach {x y} $xy {
set X($idx) $x
set Y($idx) $y
incr idx
if {$idx == 1} {
set X($idx) $x
set Y($idx) $y
incr idx
}
}
## duplicate last point
set X($idx) $x
set Y($idx) $y
incr idx
# Now generate the point list
set xy [list $X(0) $Y(0)]
for {set i 1} {$i < $np} {incr i} {
set i0 [expr {$i - 1}]
set i2 [expr {$i + 1}]
set i3 [expr {$i + 2}]
for {set j 0} {$j <= $PRECISION} {incr j} {
set mu [expr {double($j) / double($PRECISION)}]
set x [CardinalSpline $X($i0) $X($i) $X($i2) $X($i3) $a $mu]
set y [CardinalSpline $Y($i0) $Y($i) $Y($i2) $Y($i3) $a $mu]
lappend xy $x $y
}
}
return $xy
}
proc PolyLine::Cubic {xy {PRECISION 10}} {
set np [expr {[llength $xy] / 2}]
if {$np <= 1} return
set idx 0
foreach {x y} $xy {
set X($idx) $x
set Y($idx) $y
incr idx
if {$idx == 1} {
set X($idx) $x
set Y($idx) $y
incr idx
}
}
## duplicate last point
set X($idx) $x
set Y($idx) $y
incr idx
# Now generate the point list
set xy [list $X(0) $Y(0)]
for {set i 1} {$i < $np} {incr i} {
set i0 [expr {$i - 1}]
set i2 [expr {$i + 1}]
set i3 [expr {$i + 2}]
for {set j 0} {$j <= $PRECISION} {incr j} {
set mu [expr {double($j) / double($PRECISION)}]
set x [CubicInterpolate $X($i0) $X($i) $X($i2) $X($i3) $mu]
set y [CubicInterpolate $Y($i0) $Y($i) $Y($i2) $Y($i3) $mu]
lappend xy $x $y
}
}
return $xy
}
proc PolyLine::Hermite {xy tension bias {PRECISION 10}} {
set np [expr {[llength $xy] / 2}]
if {$np <= 1} return
set idx 0
foreach {x y} $xy {
set X($idx) $x
set Y($idx) $y
incr idx
if {$idx == 1} {
set X($idx) $x
set Y($idx) $y
incr idx
}
}
## duplicate last point
set X($idx) $x
set Y($idx) $y
incr idx
# Now generate the point list
set xy [list $X(0) $Y(0)]
for {set i 1} {$i < $np} {incr i} {
set i0 [expr {$i - 1}]
set i2 [expr {$i + 1}]
set i3 [expr {$i + 2}]
for {set j 0} {$j <= $PRECISION} {incr j} {
set mu [expr {double($j) / double($PRECISION)}]
set x [HermiteInterpolate $X($i0) $X($i) $X($i2) $X($i3) $mu $tension $bias]
set y [HermiteInterpolate $Y($i0) $Y($i) $Y($i2) $Y($i3) $mu $tension $bias]
lappend xy $x $y
}
}
return $xy
}
proc PolyLine::TCB {xy tension continuity bias {PRECISION 10}} {
set np [expr {[llength $xy] / 2}]
if {$np <= 1} return
set idx 0
foreach {x y} $xy {
set X($idx) $x
set Y($idx) $y
incr idx
if {$idx == 1} {
set X($idx) $x
set Y($idx) $y
incr idx
}
}
## duplicate last point
set X($idx) $x
set Y($idx) $y
incr idx
# Now generate the point list
set xy [list $X(0) $Y(0)]
for {set i 1} {$i < $np} {incr i} {
set i0 [expr {$i - 1}]
set i2 [expr {$i + 1}]
set i3 [expr {$i + 2}]
for {set j 0} {$j <= $PRECISION} {incr j} {
set mu [expr {double($j) / double($PRECISION)}]
set x [TCBSpline $X($i0) $X($i) $X($i2) $X($i3) $mu $tension $continuity $bias]
set y [TCBSpline $Y($i0) $Y($i) $Y($i2) $Y($i3) $mu $tension $continuity $bias]
lappend xy $x $y
}
}
return $xy
}
proc PolyLine::KeyFrameTCB {xy tension continuity bias {PRECISION 10}} {
set np [expr {[llength $xy] / 2}]
if {$np <= 1} return
set idx 0
foreach {x y} $xy {
set X($idx) $x
set Y($idx) $y
incr idx
if {$idx == 1} { ;## duplicate 1st pt
set X($idx) $x
set Y($idx) $y
incr idx
}
}
## duplicate last point
set X($idx) $x
set Y($idx) $y
incr idx
# Now generate the point list
set xy [list $X(0) $Y(0)]
for {set i 1} {$i < $np} {incr i} {
set i0 [expr {$i - 1}]
set i2 [expr {$i + 1}]
set i3 [expr {$i + 2}]
set X0 $X($i0)
set X1 $X($i)
set X2 $X($i2)
set X3 $X($i3)
set Y0 $Y($i0)
set Y1 $Y($i)
set Y2 $Y($i2)
set Y3 $Y($i3)
set N0 [expr {$X1 - $X0}]
set N1 [expr {$X2 - $X1}]
set N2 [expr {$X3 - $X3}]
for {set j 0} {$j <= $PRECISION} {incr j} {
set mu [expr {double($j) / double($PRECISION)}]
set x [KeyFrameTCBSpline $X0 $X1 $X2 $X3 $mu $tension $continuity $bias $N0 $N1 $N2]
set y [KeyFrameTCBSpline $Y0 $Y1 $Y2 $Y3 $mu $tension $continuity $bias $N0 $N1 $N2]
lappend xy $x $y
}
}
return $xy
} if {[file tail [info script]] == [file tail $argv0]} { ##Now to demonstrate and test the code you can use the following:
################################################################
################################################################
#
# Test harness and demo code
#
package require Tk
set S(title) "Cubic Splines with Tension"
set S(r) 5 ;# Control point size
set S(w) 5 ;# Line width
set S(precision) 10
set INITPOINTS {-200 0 -80 -125 30 100 200 0}
proc Reset {} {
global S
set S(tension) 0
set S(continuity) 0
set S(bias) 0
set S(a) 0.5
DrawCurve
}
proc BrushedMetal {c width height} {
## from wiki https://wiki.tcl-lang.org/9776
return
## for {set row 0} {$row < $height} {incr row 1} {
## set line_color [expr {45000+int(1000000*rand())%3000}]
## $c create line 0 $row $width $row -width 1
## -fill [format "#%04x%04x%04x"
## $line_color $line_color $line_color]
## }
}
proc DoDisplay {} {
global S INITPOINTS
wm title . $S(title)
pack [frame .ctrl -relief ridge -bd 2 -padx 5 -pady 5] \
-side right -fill both -ipady 5
pack [frame .screen -bd 2 -relief raised] -side top -fill both -expand 1
canvas .c -relief raised -borderwidth 0 -height 500 -width 500
BrushedMetal .c 500 500
pack .c -in .screen -side top -fill both -expand 1
bind all <Alt-c> {catch {console show}}
bind .c <Configure> {ReCenter %W %h %w}
.c bind p <B1-Motion> [list MouseMove %x %y]
bind all <Escape> {exit}
DoCtrlFrame
AddCtrlPoint $INITPOINTS
update
}
proc DoCtrlFrame {} {
frame .buttons
pack [button .buttons.add -text "Add Pt" -command AddCtrlPoint] -side left
pack [button .buttons.dele -text "Del Pt" -command DeleteCtrlPoint] -side left
pack [button .buttons.clear -text "Clear Pts" -command ClearCtrlPoint] -side left
set font {Helvetica 14 bold}
scale .prec -width 10 -orient h -variable S(precision) -font $font \
-label Precision: -relief ridge -from 1 -to 40 -command DrawCurve
scale .bias -width 10 -orient h -variable S(bias) -font $font \
-label "B - Bias:" -relief ridge -from -1. -to 1. -resolution 0.01 -command DrawCurve
scale .tens -width 10 -orient h -variable S(tension) -font $font \
-label "T - Tension:" -relief ridge -from -1. -to 1. -resolution 0.01 -command DrawCurve
scale .cont -width 10 -orient h -variable S(continuity) -font $font \
-label "C - Continuity:" -relief ridge -from -1. -to 1. -resolution 0.01 -command DrawCurve
scale .a -width 10 -orient h -variable S(a) -font $font \
-label "Cardinal Spline - A:" -relief ridge -from 0. -to 1. -resolution 0.01 -command DrawCurve
button .reset -text Reset -command {Reset}
labelframe .rb -text "INTERPOLATOR" -relief ridge -bd 2
set rbList {} ;# radio button list
lappend rbList {line "Linear"}
lappend rbList {cosi "Cosine"}
lappend rbList {cubp "Cubic Polynomial"}
lappend rbList {cubs "Cubic Spline - Keith Vetter"}
lappend rbList {catm "CatmullRom Spline"}
lappend rbList {card "Cardinal Spline (A)"}
lappend rbList {tbsp "TB Spline"}
lappend rbList {tcbs "TCB Spline"}
lappend rbList {bezi "Piecewise Bezier Spline"}
lappend rbList {fbez "Fwd Dif Piecewise Bezier Spline"}
lappend rbList {hbez "Horner Bezier Spline"}
## KeyFrame splines are drawing a linear line, not a spline for 1st segment
## I guess our assumption that we can test these splines by assuming
## the number of frames between key frames is the difference in X coordinates
## is not adequate.
## remove from GUI:
## lappend rbList {kfs "Key Frame TCB Spline"}
set i 1
foreach entry $rbList {
set key [lindex $entry 0]
set text [lindex $entry 1]
pack [frame .rb.l$i]
radiobutton .rb.l$i.$key -variable S(type) -value $key -font $font \
-width 30 -text $text -command DrawCurve -anchor w
pack .rb.l$i.$key -side top -pady 2 -anchor w -fill x
incr i
}
pack [button .buttons.about -text About -command About] -side left
pack [button .buttons.exit -text Exit -command exit] -side left
set row 1
grid .buttons -in .ctrl -row $row -sticky ew ; incr row
#grid .add -in .ctrl -row $row -sticky ew
#grid .dele -in .ctrl -row $row -sticky ew
#grid .clear -in .ctrl -row $row -sticky ew ; incr row
grid .prec -in .ctrl -row $row -sticky ew ; incr row
grid .tens -in .ctrl -row $row -sticky ew ; incr row
grid .cont -in .ctrl -row $row -sticky ew ; incr row
grid .bias -in .ctrl -row $row -sticky ew ; incr row
grid .a -in .ctrl -row $row -sticky ew ; incr row
grid .reset -in .ctrl -row $row -sticky ew ; incr row
grid .rb -in .ctrl -row $row -sticky ew ; incr row
#grid .about -in .ctrl -row $row -sticky ew ; incr row
#grid .exit -in .ctrl -row $row -sticky ew ; incr row
}
proc ReCenter {W h w} { ;# Called by configure event
foreach h2 [expr {$h / 2}] w2 [expr {$w / 2}] break
$W config -scrollregion [list -$w2 -$h2 $w2 $h2]
BrushedMetal $W [expr {2 * $w2}] [expr {2 * $h2}]
}
proc MakeBox {x y r} {
return [list [expr {$x-$r}] [expr {$y-$r}] [expr {$x+$r}] [expr {$y+$r}]]
}
proc MouseMove {X Y} {
regexp {p([0-9]+)} [.c itemcget current -tag] => who
set X [.c canvasx $X] ; set Y [.c canvasy $Y]
foreach x $::P($who,x) y $::P($who,y) break
foreach ::P($who,x) $X ::P($who,y) $Y break
.c move p$who [expr {$X - $x}] [expr {$Y - $y}]
DrawCurve
}
proc AddCtrlPoint {{xy {}}} {
global P S
set np [llength [array names P *x]]
if {$xy == {}} {
set w [expr {[winfo width .c] - 50}]
set xy [list [expr {$w * rand() - $w/2}] [expr {50 * rand() - 25}]]
}
foreach {x y} $xy {
set P($np,x) $x
set P($np,y) $y
.c create oval [MakeBox $x $y $S(r)] -tag [list p p$np] -fill yellow
incr np
}
DrawCurve
}
proc DeleteCtrlPoint {} {
global P
set np [llength [array names P *x]]
if {$np == 0} return
incr np -1
# Always delete the rightmost control point
# swap RIGHTMOST and NP then delete NP
set rightmost [lindex [lindex [SortPoints] end] end]
.c delete p$rightmost
.c itemconfig p$np -tag [list p p$rightmost]
set P($rightmost,x) $P($np,x)
set P($rightmost,y) $P($np,y)
unset P($np,x)
unset P($np,y)
DrawCurve
}
proc ClearCtrlPoint {} {
global P
.c delete p
catch {unset P}
DrawCurve
}
proc SortPoints {} {
global P
set np [llength [array names P *x]]
set xy {}
for {set i 0} {$i < $np} {incr i} {
lappend xy [list $P($i,x) $P($i,y) $i]
}
set xy2 [lsort -real -index 0 $xy]
return $xy2
}
proc DrawCurve {args} {
global S
set xy {}
foreach pt [SortPoints] { ;# Flatten point list
foreach {x y} $pt break
lappend xy $x $y
}
switch $::S(type) {
"line" { set xy [PolyLine::Linear $xy $::S(precision)] }
"cosi" { set xy [PolyLine::Cosine $xy $::S(precision)] }
"cubp" { set xy [PolyLine::Cubic $xy $::S(precision)] }
"cubs" { set xy [PolyLine::CubicSpline $xy $::S(precision)] }
"catm" { set xy [PolyLine::CatmullRom $xy $::S(precision)] }
"bezi" { set xy [PolyLine::Bezier $xy $::S(precision)] }
"fbez" { set xy [PolyLine::FDBezier $xy $::S(precision)] }
"hbez" { set xy [PolyLine::HornBezier $xy $::S(precision)] }
"tbsp" { set xy [PolyLine::Hermite $xy $::S(tension) $::S(bias) $::S(precision)] }
"tcbs" { set xy [PolyLine::TCB $xy $::S(tension) $::S(continuity) $::S(bias) $::S(precision)] }
"card" { set xy [PolyLine::Cardinal $xy $::S(a) $::S(precision)] }
"kfs" { set xy [PolyLine::KeyFrameTCB $xy $::S(tension) $::S(continuity) $::S(bias) $::S(precision)] }
}
.c delete cubic
if {$xy == {}} return
.c create line $xy -tag cubic -width $::S(w)
.c lower cubic
}
proc About {} {
set msg "Tension Splines
by Greg Blair September 2003
[email protected]
GUI derived from
Cubic Splines
by Keith Vetter, March 2003"
tk_messageBox -title About -message $msg
}
################################################################
################################################################
DoDisplay
set S(type) line
Reset
DrawCurve
##In the above code, the part of [PolyLine::CubicSpline] that comes after Now generate
##the point list does such a conversion, but it is rather crude. Approximation with
##polygons is not bad as such (indeed, it is what Postscript does internally when it
##flattens paths), but in general one would want the number of line segments to be
##adjusted to the actual curve, so that the "precision" really would give a bound on
##the approximation error. I don't know how one would achieve this effectively, but
##there are probably good algorithms in the literature.
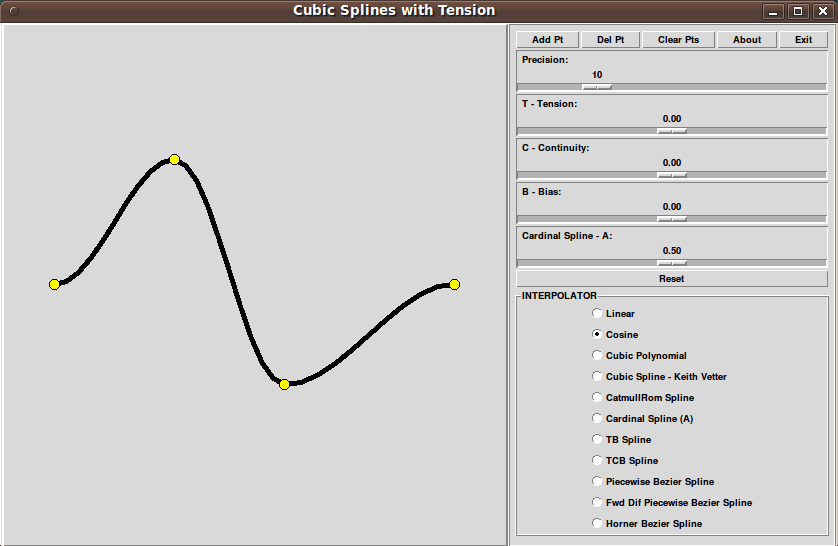
}uniquename 2013aug18
Since images at 'external sites' (such as www3.sympatico.ca above) tend to go dead, here is a screenshot image 'locally stored' on the disk drives of the server of this wiki. This image was created from the code above, but to fit the GUI on a netbook screen (max of 600 pixels high), the size 14 font was changed to 7 --- and a '-pady 0' parameter was added to 'button' and 'radiobutton' definitions. Also the '-width' (height) of the 'scale' widgets was reduced to 6 pixels.