The Recaman's sequence
GS The Recaman's sequence is a sequence invented by Bernardo Recaman Santos (a Colombian mathematician). It is defined by :
a(0) = 0 a(n) = a(n-1) - n for n > 0, if positive and not already in the sequence a(n) = a(n-1) + n otherwise
The first terms of the sequence are:
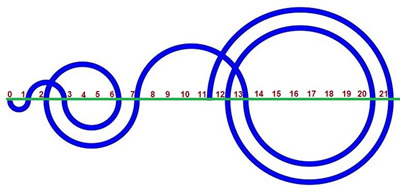
0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, 24, 8, 25, 43, 62, 42, 63, 41, 18, 42, 17, 43, 16, 44, 15, 45, 14, 46, 79, ....
An interesting visualization of this sequence can be done with half-circle representing the jump from a(n) to a(n+1).
The idea of plotting the Recaman sequence like this come from the YouTube channel Numberphile in a video featuring Alex Bellos and Edmund Harriss.
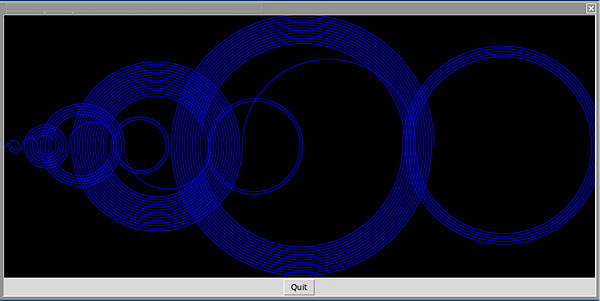
With n = 100 :
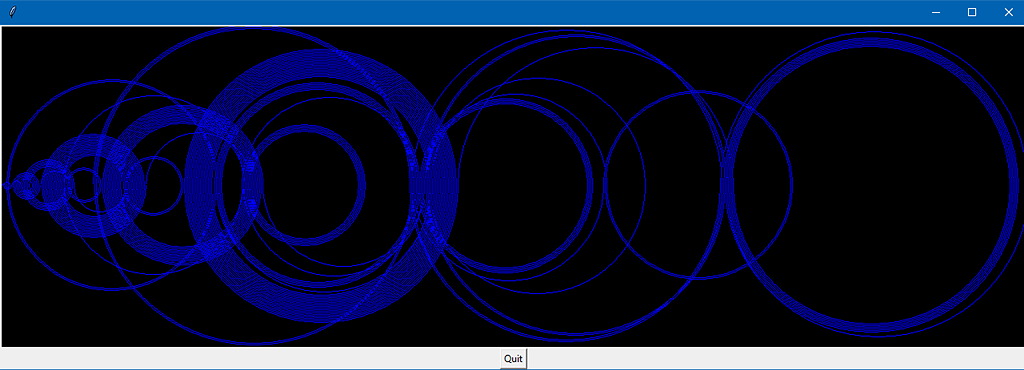
With n = 200 :
# recaman.tcl
# Author: Gerard Sookahet
# Date: 15 Apr 2021
# Description: Plot Recaman sequence with half-circles
# Reference : Numberphile - https://www.youtube.com/watch?v=FGC5TdIiT9U
package require Tk
bind all <Escape> {exit}
proc recaman {n} {
if {$n <= 0} return
set s {}
lappend s 0
set prev 0
for {set i 1} {$i <= $n} {incr i} {
set curr [expr {$prev - $i}]
if {$curr < 0 || $curr in $s} then {set curr [expr {$prev + $i}]}
lappend s $curr
set prev $curr
}
return $s
}
proc plot_recaman {s} {
set n [llength $s]
incr n -1
set z 4
set H [expr {4*$n}]
if {$n > 100} then {
set z 2
set H [expr {2*$n}]
}
set W [expr {9*$n}]
set n2 [expr {$H/2}]
pack [canvas .c -background black -width $W -height $H]
pack [button .b -text Quit -command exit]
set x1 0
for {set i 1} {$i <= $n} {incr i} {
set x2 [expr {$z*[lindex $s $i]}]
set xo [expr {($x2 - $x1)/2}]
if {$i % 2 == 0} then {
set y1 [expr {$n2 - $xo}]
set y2 [expr {$n2 + $xo}]
set ext 180
} else {
set y1 [expr {$n2 + $xo}]
set y2 [expr {$n2 - $xo}]
set ext -180
}
.c create arc $x1 $y1 $x2 $y2 -extent $ext -style arc -outline blue
set x1 $x2
}
}
plot_recaman [recaman 100]Reference :
- Numberphile - https://www.youtube.com/watch?v=FGC5TdIiT9U
For those who estimate codegolfing [L1 ] :
proc R n {lappend L [expr {$n?[set x [lindex [set L [A [expr $n-1]]] e]]>$n&$x-$n ni$L?$x-$n:$x+$n:0}]}much faster (ten times!!) Recaman Sequence implementation. the code can also be easily converted for the coroutines/generator
proc recaman { total } {
if { $total <= 0 } {
return {}
}
set recaman {}
array set unused {} ; # unused numbers
set maxnum 1 ; # max of unused +1
set current 0
for { set i 1 } { $i<$total } { incr i } {
set n [ expr { $current - $i } ]
if { $n > 0 && [ info exists unused($n) ] } {
unset unused($n)
} else {
set n [ expr { $current + $i } ]
if { $n >= $maxnum } {
for { set maxnum } { $maxnum < $n } { incr maxnum } {
set unused($maxnum) $maxnum
}
incr maxnum
} else {
if { [ info exists unused($n) ] } {
unset unused($n)
} else {
# puts "dup $n"
}
}
}
set current $n
lappend recaman $n
}
set recaman
}