TkPNG

PNG Photo Image extension for Tcl/Tk

MAK (08 Mar 2005)

This package implements support for loading and using PNG images with Tcl/Tk. Although other extensions such as Img also add support for PNG images, I wanted something that was lightweight, did not depend on libpng, and which would be suitable for inclusion in the Tk core, as Tk does not currently support any image formats natively that take advantage of its internal support for alpha blending, and alpha antialiasing and drop shadows really go a long way toward beautifying Tk applications.

The package supports the full range of color types, channels and bit depths from 1 bit black & white to 16 bit per channel full color with alpha (64 bit RGBA) and interlacing. Ancillary "chunks" such as gamma, color profile, and text fields are ignored, although they are checked at a minimum for correct CRC.

Home Page: http://www.muonics.com/FreeStuff/TkPNG/

The windows makefile.vc still needs to be modified to find zlib, though..

Here's a teaser using Tile labels and Willem van Schaik's suite of PNG test images [L1 ]:

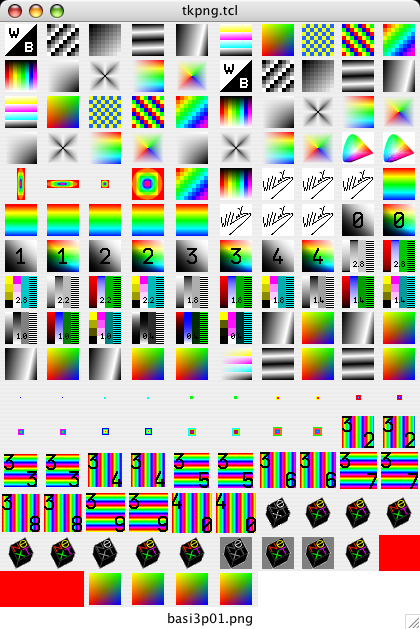
Of course it looks the same as Img, but its only dependency is on zlib, which already has a TIP.

The functionality of TkPNG is scheduled to inclusion in Tcl/Tk 8.5 as TIP 244 [L2 ]

I ran some benchmarks and it ranges from slightly slower to much slower than Img depending on the image size. Much of that time is spent in filtering, and I think I can rewrite it to optimize it a fair bit. I think it also may be filtering the first scan line of each pass (of 7) in interlaced images when it's not supposed to. Since 3 of the 4 line filter modes (not including "none") mix a scan line with the previous scan line in the current pass, I'm surprised not to see images that look wrong. I guess the PNG suite doesn't cover that particular situation well.

At any rate, I think with a big of optimizing I may be able to make it faster than Img.

This is really great work. Keep it up! Once you get the base64 code done, I've got all I need. I really hate including the entirety of Img just to get PNG (the only format I really care about) support. Thanks for the work! -- DC 03/11/05

MAK (19 Mar 2005) New version 0.6. Base 64 decoding support was added, and several optimizations were made.

AJB (22 Mar 2005) Very nice! Ive managed to compile 0.6 for most platforms that I need it on. However, if someone has a macosx binary, could you please post a link here. It would be appreciated, as I dont really feel like going through that learning curve right now. :) (MAK - There's now an OSX binary at the SF download page for 0.7.)

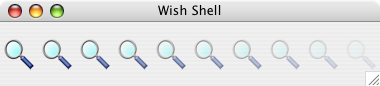
MAK (26 Mar 2005) New version 0.7. You can now modify the overall image transparency at creation time with, e.g.:

 image create photo -format "png -alpha 0.5" example.png

Here's a little display of progressive alpha values between 1.0 and 0.1. These are all from the same image file:

RT Indeed PNG would be nice to have in the core for many uses. Since Img is long established, I hope that the eventual TIP'ed implementation will be such that the user can still choose the Img PNG code for peace of mind. IOW, PNG in the core shouldn't prevent opting to use the Img extension's PNG. Thanks, Roy Terry, 27Mar05

LV Perhaps the Img PNG support could be refactored to make use of the Tk core PNG (once that happens, if it does), and that way less code need be distributed with Img.

DKF: TkPNG has formed the basis for the PNG format support that will form part of 8.6 (not in 8.6b1; couldn't get it done in time, sorry...)

DDG: A starkit for Tclkit 8.4 and 8.5 with binary build for Win32-x86, Linux-x86 and Darwin-X86 (X11) is available here: https://bitbucket.org/mittelmark/tcl-code/wiki