Ulam spiral
GS - The Ulam Spiral was created in 1963 by the mathematician Stanislaw Ulam while he got bored during a talk at a scientific meeting. He decided to put integers on a square grid following a spiral pattern, and he checked prime numbers. Some primes seems to appear according to nonrandom patterns or straight lines.

He published two articles about its discovery: - S.M. Ulam, M.L. Stein and M.B. Wells, A Visual Display of Some Properties of the Distribution of Primes, American Mathematical Monthly (71), pp516-520, 1964. - S.M. Ulam and M.L. Stein, An Observation on the Distribution of Primes, American Mathematical Monthly (74), pp43-44, 1967.
In 1988, Jean-François Colonna of the Ecole Polytechnique (France) generalized this spiral. Instead of checking only primes, he represents all the integer with a color table corresponding to their number of divisors.
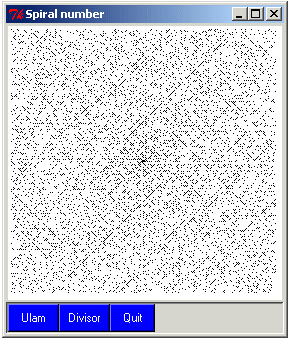

If we represents only integers with an odd number of divisors (not done here), they are all perfect square, and they all belong to the same diagonal. So there are more integers with even number of divisors than with odd number.
# spiral.tcl
# Author: Gerard Sookahet
# Date: 03 May 2004
# Description: Ulam spiral and divisor spiral on a square grid
package require Tk
proc SpiralMain { N } {
set w .sp
catch {destroy $w}
toplevel $w
wm withdraw .
wm title $w "Spiral number"
wm geometry $w +100+10
set dim [expr {int(sqrt($N) + 10)}]
set mid [expr {$dim/2}]
pack [canvas $w.c -width $dim -height $dim -bg white]
set f1 [frame $w.f1 -relief sunken -borderwidth 2]
pack $f1 -fill x
button $f1.bu -text Ulam -width 6 -bg blue -fg white \
-command "PlotUlam $w $N $mid"
button $f1.bd -text Divisor -width 6 -bg blue -fg white \
-command "PlotDivisor $w $N $mid"
button $f1.bq -text Quit -width 5 -bg blue -fg white -command exit
eval pack [winfo children $f1] -side left
}
proc PlotUlam { w N mid } {
$w.c delete all
set pix [image create photo]
$w.c create image 0 0 -anchor nw -image $pix
set cmap #030303
set i $mid
set j $mid
# Spiral initialization by hand for 1 2 3 4 5 6 7
$pix put $cmap -to $i $j
incr i
$pix put $cmap -to $i $j
incr j -1
$pix put $cmap -to $i $j
incr i -1
$pix put $cmap -to $i $j
incr i -1
$pix put $cmap -to $i $j
incr j
$pix put $cmap -to $i $j
incr j
$pix put $cmap -to $i $j
set n 7
set m 3
set M [expr {int(sqrt($N))}]
while {$m < $M} {
for {set k 1} {$k <= $m} {incr k} {
incr n
incr i
if [IsPrime $n] {$pix put $cmap -to $i $j}
}
for {set k 1} {$k <= $m} {incr k} {
incr n
incr j -1
if [IsPrime $n] {$pix put $cmap -to $i $j}
}
set mm [expr {$m + 1}]
for {set k 1} {$k <= $mm} {incr k} {
incr n
incr i -1
if [IsPrime $n] {$pix put $cmap -to $i $j}
}
for {set k 1} {$k <= $mm} {incr k} {
incr n
incr j
if [IsPrime $n] {$pix put $cmap -to $i $j}
}
update idletasks
incr m 2
}
}
proc PlotDivisor { w N mid } {
$w.c delete all
set pix [image create photo]
$w.c create image 0 0 -anchor nw -image $pix
set cmap #030303
set i $mid
set j $mid
# Spiral initialization by hand for 1 2 3 4 5 6 7
$pix put $cmap -to $i $j
incr i
$pix put $cmap -to $i $j
incr j -1
$pix put $cmap -to $i $j
incr i -1
$pix put [colormap 1] -to $i $j
incr i -1
$pix put $cmap -to $i $j
incr j
$pix put [colormap 2] -to $i $j
incr j
$pix put $cmap -to $i $j
set n 7
set m 3
set M [expr {int(sqrt($N))}]
while {$m < $M} {
for {set k 1} {$k <= $m} {incr k} {
incr n
incr i
$pix put [colormap [NbDivisor $n]] -to $i $j
}
for {set k 1} {$k <= $m} {incr k} {
incr n
incr j -1
$pix put [colormap [NbDivisor $n]] -to $i $j
}
set mm [expr {$m + 1}]
for {set k 1} {$k <= $mm} {incr k} {
incr n
incr i -1
$pix put [colormap [NbDivisor $n]] -to $i $j
}
for {set k 1} {$k <= $mm} {incr k} {
incr n
incr j
$pix put [colormap [NbDivisor $n]] -to $i $j
}
update idletasks
incr m 2
}
}
# Primality testing
proc IsPrime { n } {
set max [expr {int(sqrt($n))}]
set d 2
while {$d <= $max} {
if {$n%$d == 0} {return 0}
incr d
}
return 1
}
# Return the number of divisors of an integer
proc NbDivisor { n } {
set max [expr {int(sqrt($n))}]
set nd 0
for {set i 2} {$i <= $max} {incr i} {
if {$n%$i == 0} {incr nd}
}
return $nd
}
# Arbitrary color table
proc colormap { n } {
set lcolor {#030303 #CD0000 #CD4F39 #EE4000 #EE6A50 #FF7F00 #EE9A00 \
#FF8C69 #FFC125 #EEEE00 #EED5B7 #D2691E #BDB76B #00FFFF \
#7FFFD4 #FFEFD5 #AB82FF #E066FF
}
return [lindex $lcolor $n]
}
# The maximum integer. The canvas is sized from its square root
SpiralMain 70000