Universal Transverse Mercator
Keith Vetter 2004-04-15 : Universal Transverse Mercator (UTM) is another coordinate system for the earth that has some nice advantages over the more familiar latitude and longitude especially at large scales. The TerraServer online database of USGS topo maps and aerial photographs is based on UTM coordinates (see TkTopomap).
The basic idea behind UTM is that the world is divided into 60 north-south zones. Within each zone, a coordinate is measured in meters north from the equator--northing--and meters east from a central meridian--easting. For gory details see http://mac.usgs.gov/mac/isb/pubs/factsheets/fs07701.html or [broken www.nps.gov/prwi/readutm.htm]: try [L1 ].
Below are two routines to convert from UTM into lat/lon and vice versa. It uses the WGS-84 datum but a table is provided if you want to use other ones. As usual a simple demo is also provided (warning, absolutely no error checking is done.)
##+############################################################# #############
#
# ll2utm -- Converts latitude and longitude into Universal Transverse
# Mercator (UTM) coordinates. Lots of fun math which I got off the
# web.
#
proc ll2utm {latitude longitude} {
set PI [expr {atan(1) * 4}]
set K0 0.9996
# WGS-84
set er 6378137 ;# EquatorialRadius
set es2 0.00669438 ;# EccentricitySquared
set es4 [expr {$es2 * $es2}]
set es6 [expr {$es2 * $es2 * $es2}]
# Must be in the range -180 <= long < 180
while {$longitude < -180} { set longitude [expr {$longitude + 360}]}
while {$longitude >= 180} { set longitude [expr {$longitude - 360}]}
# Now convert
set lat_rad [expr {$latitude * $PI / 180.0}]
set long_rad [expr {$longitude * $PI / 180.0}]
set zone [expr {int(($longitude + 180) / 6) + 1}]
if {$latitude >= 56.0 && $latitude < 64.0 &&
$longitude >= 3.0 && $longitude < 12.0} {
$zone = 32
}
if { $latitude >= 72.0 && $latitude < 84.0 } {
if { $longitude >= 0.0 && $longitude < 9.0 } {$zone = 31;}
if { $longitude >= 9.0 && $longitude < 21.0 } {$zone = 33;}
if { $longitude >= 21.0 && $longitude < 33.0 } {$zone = 35;}
if { $longitude >= 33.0 && $longitude < 42.0 } {$zone = 37;}
}
# +3 puts origin in middle of zone
set long_origin [expr {( $zone - 1 ) * 6 - 180 + 3}]
set long_origin_rad [expr {$long_origin * $PI / 180.0}]
set eccPrimeSquared [expr {$es2 / ( 1.0 - $es2 )}]
set N [expr {$er / sqrt( 1.0 - $es2 * sin( $lat_rad ) * sin( $lat_rad ) )}]
set T [expr {tan( $lat_rad ) * tan( $lat_rad )}]
set C [expr {$eccPrimeSquared * cos( $lat_rad ) * cos( $lat_rad )}]
set A [expr {cos( $lat_rad ) * ( $long_rad - $long_origin_rad )}]
set M [expr { $er * ( \
(1.0 - $es2 / 4 - 3 * $es4 / 64 - 5 * $es6 / 256) * $lat_rad \
- (3 * $es2 / 8 + 3 * $es4 / 32 + 45 * $es6 / 1024) * sin(2 * $lat_rad) \
+ (15 * $es4 / 256 + 45 * $es6 / 1024 ) * sin(4 * $lat_rad) \
- (35 * $es6 / 3072 ) * sin(6 * $lat_rad) \
)}]
set easting [expr {$K0 * $N * ( $A + ( 1 - $T + $C ) * $A * $A * $A / 6 \
+ ( 5 - 18 * $T + $T * $T + 72 * $C - 58 * $eccPrimeSquared ) * \
$A * $A * $A * $A * $A / 120 ) + 500000.0}]
set northing [expr {$K0 * ( $M + $N * tan( $lat_rad ) * \
( $A * $A / 2 + ( 5 - $T + 9 * $C + 4 * $C * $C ) * \
$A * $A * $A * $A / 24 + ( 61 - 58 * $T + $T * $T + \
600 * $C - 330 * $eccPrimeSquared ) * \
$A * $A * $A * $A * $A * $A / 720 ) )}]
if {$latitude < 0} { ;# 1e7 meter offset for southern hemisphere
set northing [expr {$northing + 10000000.0}]
}
set northing [expr {int($northing)}]
set easting [expr {int($easting)}]
if {$latitude > 84.0 || $latitude < -80.0} {
set letter "Z"
} else {
set l [expr {int(($latitude + 80) / 8.0)}]
set letter [string index "CDEFGHJKLMNPQRSTUVWXX" $l]
}
return [list $northing $easting $zone $letter]
}
##+##########################################################################
#
# utm2ll -- Converts Universal Transverse Mercator (UTM) into
# latitude and longitude coordinates. More fun math which I got off
# the web.
#
proc utm2ll {northing easting zone {letter S}} {
set PI [expr {atan(1) * 4}]
set K0 0.9996
# WGS-84
set er 6378137 ;# EquatorialRadius
set es2 0.00669438 ;# EccentricitySquared
set es2x [expr {1.0 - $es2}]
set x [expr {$easting - 500000.0}]
set northernHemisphere [expr {$letter >= "N"}]
set y [expr {$northing - ($northernHemisphere ? 0.0 : 10000000.0)}]
set long_origin [expr {($zone - 1) * 6 - 180 + 3}] ;# +3 puts in middle
set ep2 [expr {$es2 / $es2x}]
set e1 [expr {(1.0 - sqrt($es2x)) / (1.0 + sqrt($es2x))}]
set M [expr {$y / $K0}]
set mu [expr {$M / ($er * (1.0 - $es2 /4.0 - 3 * $es2 * $es2 /64.0
- 5 * $es2 * $es2 * $es2 /256.0))}]
set phi [expr {$mu + (3 * $e1 / 2 - 27 * $e1 * $e1 * $e1 / 32 ) * sin(2*$mu)
+ (21 * $e1 * $e1 / 16 - 55 * $e1 * $e1 * $e1 * $e1 / 32) *
sin(4*$mu ) + (151 * $e1 * $e1 * $e1 / 96 ) * sin(6*$mu)}]
set N1 [expr {$er / sqrt(1.0 - $es2 * sin($phi) * sin($phi))}]
set T1 [expr {tan($phi) * tan($phi)}]
set C1 [expr {$ep2 * cos($phi) * cos($phi)}]
set R1 [expr {$er * $es2x / pow(1.0 - $es2 * sin($phi) * sin($phi), 1.5)}]
set D [expr {$x / ($N1 * $K0)}]
set latitude [expr {$phi - ($N1 * tan($phi) / $R1) * ($D * $D / 2
- (5 + 3 * $T1 + 10 * $C1 - 4 * $C1 * $C1 - 9 * $ep2) *
$D * $D * $D * $D / 24
+ (61 + 90 * $T1 + 298 * $C1 + 45 * $T1 * $T1
- 252 * $ep2 - 3 * $C1 * $C1 ) * $D * $D * $D * $D * $D * $D / 720)}]
set latitude [expr {$latitude * 180.0 / $PI}]
set longitude [expr {($D - (1 + 2 * $T1 + $C1) * $D * $D * $D / 6
+ (5 - 2 * $C1 + 28 * $T1 - 3 * $C1 * $C1
+ 8 * $ep2 + 24 * $T1 * $T1) * $D * $D * $D * $D * $D / 120)
/ cos($phi)}]
set longitude [expr {$long_origin + $longitude * 180.0 / $PI}]
return [list $latitude $longitude]
}
## Other datums which could be used here instead:
##
## Name EquatorialRadius EccentricitySquared
## ---- ---------------- -------------------
## Airy 6377563 0.00667054
## Australian National 6378160 0.006694542
## Bessel 1841 6377397 0.006674372
## Bessel 1841 (Nambia) 6377484 0.006674372
## Clarke 1866 6378206 0.006768658
## Clarke 1880 6378249 0.006803511
## Everest 6377276 0.006637847
## Fischer 1960 (Mercury) 6378166 0.006693422
## Fischer 1968 6378150 0.006693422
## GRS 1967 6378160 0.006694605
## GRS 1980 6378137 0.00669438
## Helmert 1906 6378200 0.006693422
## Hough 6378270 0.00672267
## International 6378388 0.00672267
## Krassovsky 6378245 0.006693422
## Modified Airy 6377340 0.00667054
## Modified Everest 6377304 0.006637847
## Modified Fischer 1960 6378155 0.006693422
## South American 1969 6378160 0.006694542
## WGS 60 6378165 0.006693422
## WGS 66 6378145 0.006694542
## WGS-72 6378135 0.006694318
## WGS-84 6378137 0.00669438
################################################################
#
# DEMO code
#
package require Tk
proc DoDisplay {} {
labelframe .ll -text "Lat/Lon" -padx 5
label .ll.lat -text Latitude:
entry .ll.elat -textvariable C(lat)
label .ll.lon -text Longitude:
entry .ll.elon -textvariable C(lon)
grid .ll.lat .ll.elat -sticky w
grid .ll.lon .ll.elon -sticky w
grid rowconfigure .ll 1000 -weight 1
labelframe .utm -text UTM -padx 5
label .utm.north -text Northing:
entry .utm.enorth -textvariable C(north)
label .utm.east -text Easting:
entry .utm.eeast -textvariable C(east)
label .utm.zone -text Zone:
entry .utm.ezone -textvariable C(zone)
label .utm.letter -text Letter:
entry .utm.eletter -textvariable C(letter)
grid .utm.north .utm.enorth -sticky w
grid .utm.east .utm.eeast -sticky w
grid .utm.zone .utm.ezone -sticky w
grid .utm.letter .utm.eletter -sticky w
frame .2
button .2.utm -text "==>" -command [list Convert 1]
button .2.ll -text "<==" -command [list Convert 0]
grid .2.utm -pady 5
grid .2.ll
grid .ll .2 .utm -sticky ns -pady {5 10} -padx 5
grid configure .2 -padx 20
image create photo ::img::blank -width 1 -height 1
button .about -image ::img::blank -highlightthickness 0 -command \
[list tk_messageBox -message "UTM Converter\nby Keith Vetter\nMarch, 2004"]
place .about -in . -relx 1 -rely 1 -anchor se
focus .ll.elat
}
proc lat2dec {value} {
set cnt [scan "$value 0 0 0" "%g %g %g" l1 l2 l3]
set dec [expr {abs($l1) + $l2 / 60.0 + $l3 / 3600.0}]
if {$l1 < 0} {set dec [expr {-1 * $dec}]}
return $dec
}
proc Convert {toUTM} {
global C
if {$toUTM} {
foreach var {north east zone letter} { set C($var) "" }
foreach var {lat lon} {
set C($var) [string trim $C($var)]
if {$C($var) eq ""} return
set $var [lat2dec $C($var)]
}
set utm [ll2utm $lat $lon]
foreach {C(north) C(east) C(zone) C(letter)} $utm break
} else {
foreach var {lat lon} { set C($var) "" }
foreach var {north east zone letter} {
set C($var) [string trim $C($var)]
if {$C($var) eq "" && $var ne "letter"} return
}
set ll [utm2ll $C(north) $C(east) $C(zone) $C(letter)]
foreach {C(lat) C(lon)} $ll break
}
}
DoDisplay
set C(lat) "40 4 4.5"
set C(lon) [lat2dec "-82 31 12.6"]PWE: The first line of ll2utm proc
if {$longitude > 0} {set longitude [expr {-1 * $longitude}]} makes this code correct for only the western hemisphere. Probably more correct is to remove the first line and enter western hemisphere longitudes as negative numbers (as seems to be the normal convention). fixed
PD: These formulae appear to be the same as in Snyder http://onlinepubs.er.usgs.gov/djvu/PP/PP_1395.pdf - see formulae 8-9 to 8-25. This is very slow. A better solution would involve an extension to use the proj.4 library http://trac.osgeo.org/proj/wiki/ProjAPI
Screenshots
uniquename 2013aug18
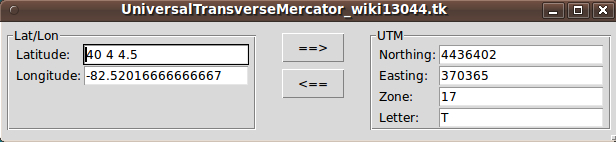
The screenshot above is on an 'external' site (flickr) and is likely to go dead. Also the image is too small to read the text. Here is another screenshot of the UTM GUI --- 'locally stored', on the disk drives of the server of this wiki --- a larger image.
When the GUI first came up, the entry fields on the right were blank. A click on the right-arrow caused those entry fields to be filled.
That little dimple on the lower right corner of the GUI is like the 'About' button on many of Vetter's other GUI's. If you click on it, a popup shows the text 'UTM Converter, by Keith Vetter, 2004'. You can see the definition of that button in the code above.
Related topics: geodesy