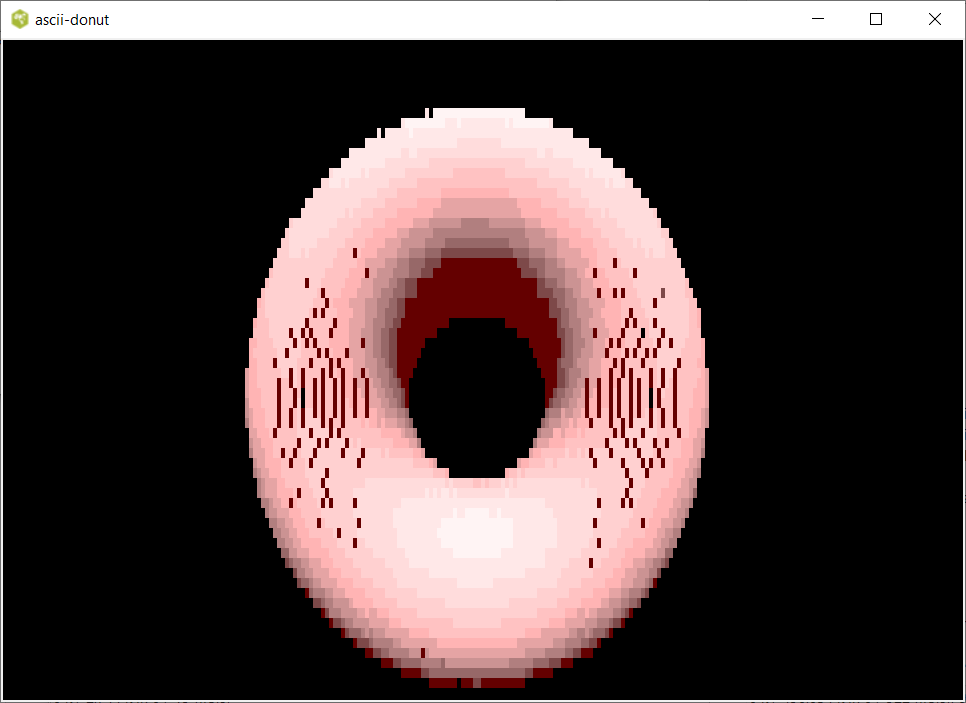
ASCII donut transcribed
Arjen Markus (31 october 2021) I was intrigued by a small Fortran program that presents a doughnut shape in ASCII art. The idea has been implemented in all manner of languages, as a quick search on the internet shows. Rather than transcribing it literally and create yet another ASCII art producing program in Tcl, I thought it would be nice to use the canvas instead.
The transcription was straightforward - just a bit of juggling the size of the rectangles to get a nice display. Perhaps the hardest part was to determine the colours to be used in stead of the characters. I opted for a sequence of red shades and to calculate the RGb values rather than via named colours, it is far easier that way ;).
Here is the code, it leaves some holes in the images, because the rectangles do not cover the doughnut shape contiguously, but I think it is a charming aspect.
# ascii-donut.tcl --
# Transcription of the "ASCII-Donut-Fortran" code to Tcl/Tk
# The souerce code that I transcribed is at:
# https://github.com/ShrirajHegde/ASCII-Donut-Fortran/blob/main/donut.f90
#
# Rather than ASCII art it uses the canvas
#
set scale 3
set width [expr {80 * $scale}] ;# 80 * 3 = 240 -> factor 3
set height [expr {22 * $scale}] ;# 22 * 3 = 66 -> factor 10
pack [canvas .c -width [expr {4 * $width}] -height [expr {10 * $height}] -bg black]
#
# Create the rectangles
#
set wdelta 4
set hdelta 10
for {set h 0} {$h < $height} {incr h} {
for {set w 0} {$w < $width} {incr w} {
set x1 [expr {$w * $wdelta}]
set x2 [expr {$x1 + $wdelta}]
set y1 [expr {$h * $hdelta}]
set y2 [expr {$y1 + $hdelta}]
lappend id [.c create rectangle $x1 $y1 $x2 $y2 -fill black -outline {} -tag ID]
lappend z_buffer_0 0.0
}
}
#
# Create the shades for the doughnut
#
for {set i 0} {$i < 12} {incr i} {
set x1 [expr {50*$i}]
set x2 [expr {$x1 + 49}]
set r [expr {100 + (155 * min($i,6)) / 6}]
set b [expr { int(255 * sqrt($i/12.0))}]
set g $b
lappend colours [format "#%2.2x%2.2x%2.2x" $r $g $b]
}
set speed 0.4
set tau [expr {3.14159 * 2.0}]
set angle_x 0.0
set angle_y 0.0
console show
while {1} {
set z_buffer $z_buffer_0
.c itemconfigure ID -fill black
set theta 0.0
while { $theta < $tau } {
set phi 0.0
while { $phi < $tau } {
set sinphi [expr { sin($phi) }]
set costheta [expr { cos($theta) }]
set cosjthetap2 [expr { $costheta+2.0 }]
set sinax [expr { sin($angle_x) }]
set sintheta [expr { sin($theta) }]
set cosax [expr { cos($angle_x) }]
set cosphi [expr { cos($phi) }]
set cosay [expr { cos($angle_y) }]
set sinay [expr { sin($angle_y) }]
set mess [expr { 1.00 / ($sinphi*$cosjthetap2*$sinax + $sintheta*$cosax + 5.0) }]
set t [expr { $sinphi*$cosjthetap2*$cosax - $sintheta*$sinax }]
set xcrd [expr { int(40.0*$scale+$scale*30.0*$mess*($cosphi*$cosjthetap2*$cosay - $t*$sinay)) }]
set ycrd [expr { int($scale*12.0+$scale*15.0*$mess*($cosphi*$cosjthetap2*$sinay + $t*$cosay)) }]
set idx [expr { $xcrd+$width*$ycrd }]
set lum [expr { int(8.0*(($sintheta*$sinax - $sinphi*$costheta*$cosax)*$cosay-$sinphi*$costheta*$sinax - $sintheta*$cosax-$cosphi *$costheta*$sinay)) }]
if { $height > $ycrd && $ycrd > 0 && $xcrd > 0 && $width > $xcrd && $mess > [lindex $z_buffer $idx] } {
lset z_buffer $idx $mess
if { $lum > 0 } {
.c itemconfigure $idx -fill [lindex $colours $lum]
} else {
.c itemconfigure $idx -fill [lindex $colours 0]
}
}
set phi [expr { $phi + 0.02 }]
}
set theta [expr {$theta + 0.07 }]
}
set angle_x [expr { $angle_x+0.04*$speed }]
set angle_y [expr { $angle_y+0.04*$speed }]
after 200 {
set next 1
}
vwait next
}