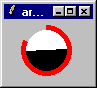
An arc clock

Richard Suchenwirth 2004-12-25 - I don't know why, but this Xmas somehow unusual clocks interest me most. Here's a very simple one with 24 hour display (the black/white disk) plus minutes (the red arc running round the disk).

See Also

A little A-D clock

A base-5 clock

Sunrise and Sunset

ttt 2016-09-30 10:17:52: Sunrise and Sunset calulation.

Description

Black and white obviously stand for day and night; by the angle of the black/white divide you can tell the hour (noon is horizontal with white up, midnight is horizontal with black up) measured at top of the disk. The minute display allows reading at roughly 5 minutes precision. The screenshot was taken at 11:49.

The GUI is just a canvas with three items:

package require Tk

pack [canvas .c -width 60 -height 60]
.c create arc 5 5 55 55 -fill red -outline red \
   -start 90 -tag min
.c create oval 10 10 50 50 -fill white -outline white
.c create arc 10 10 50 50 -fill black -extent 180 -tag night
-- I need this [every] now and then :)
proc every {ms body} {eval $body; after $ms [namespace code [info level 0]]}

proc update'arc'clock w {
    scan [clock format [clock sec] -format %H] %d hour
    scan [clock format [clock sec] -format %M] %d minute
    $w itemconfig night -start [expr ($hour+$minute/60.)*-15]
    $w itemconfig min -extent [expr $minute*-6]
}

every 1000 {update'arc'clock .c}

bind . <Escape> {exec wish $argv0 &; exit}

rmax: Here is a slight variation of update'arc'clock that uses the red arc to represent both, minutes and seconds:}

proc update'arc'clock w {
    set sec [clock sec]
    scan [clock format $sec -format %H] %d hour
    scan [clock format $sec -format %M] %d minute
    scan [clock format $sec -format %S] %d second
    $w itemconfig night -start [expr ($hour+$minute/60.)*-15]
    $w itemconfig min -start [expr $minute*-6+90]
    $w itemconfig min -extent [expr (60-$minute+$second)*-6]
}

Too bad no one got you a Time By Design [L1 ] watch for Christmas ;) This is somewhat like their pie watch. - RS can't see that page, as it requires a Flash player - but I'm less interested in consumer goods than in the freedom of being my own clockmaker :^) A happy new year to all!

rdt: As usual with your projects, this is great. It would be nice if the half-white/half-black could reflect the actual daylight/nightime ratio. But I don't know how to even get that information. Maybe even show the dusk/dawn time period in gray? Of course for those above the arctic circle it might be a pain. - RS:) Hm.. The day/night ratio is 1:1 on the equinoxes (21 March/21 Sep), and depending on hemisphere varies on other dates. But I thought it is challenging enough for the user to estimate the angle of a straight line in 15 degrees units (360 degrees/24 h)... rdt Well, you certainly are right about that. I was thinking about one pixel tick marks around the edge of the circle with noon/midnight being 3 pixel lines. But, I guess thats a bit too much work. Anyone know where to get or calculate the dawn, sunrise, dusk, sunset times?

GWM: See [L2 ] for an approximate formula. Note the need for correction for "the equation of time" which is NOT included here. This can make set & rise up to 15 minutes earlier or later [L3 ]. However the effect of refraction so that the sun is seen even when geometrically below the horizon is included (the constant 0.8333). See mathforum reference for other suggested values of the refraction constant.

set pi [expr {4*atan(1)}]
set L 51.0 ;# latitude of observation
set longitude 4 ;# Cornwall UK, 240 miles west of Greenwich
set hours 0   ;# correction for time zone, eg -1 for most of Europe except Ireland, UK, Portugal.
set J 0
while {$J<360} {
    set p [expr {asin(.39795*cos(.2163108 + 2*atan(.9671396*tan(.00860*($J-186))))) } ]
    set D [expr {sin(0.8333*3.14159/180) + sin($L*$pi/180)*sin($p)/(cos($L*$pi/180)*cos($p))}]
    if {$D>1} { set D 1 }   ;# limit for arc cos function
    if {$D<-1} { set D -1 }
    set D [expr {24 - (24/$pi)*acos($D)}]
    puts "Day $J has daylength $D rise [expr {12+$hours-$D/2-$longitude/15.}] sets [expr {12+$hours+$D/2-$longitude/15.}]"
    incr J 5
}

where

  D is daylength (to be solved)
  L = latitude in degrees
  J = day of the year starting Jan 1, -186 corrects for the shortest day being Dec 21 not Jan 1
     (when -182 would be appropriate). I think that the value should be -188 but values are from the reference.

The above formulae have been fixed for when the day length approaches or exceeds 24 hours (eg latitude>67.5, longest day of year). If your longitude is not at exactly zero (the meridian of your local time zone, here Greenwich) then a correction of 4 minutes per degree is applied to rise & set times. The times can be checked with [L4 ]

If your local time zone is not Greenwich then correct your rise/set time by N hours. Also correct for Summer Time (BST is Greenwich+1 hour) (Daylight Saving). And convert from decimal hours to hours, minutes.