Babylonian Number Series and eTCL demo example calculator
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 12Dec2018
- Following series were not proven known to Babylonians or Babylonian notation
- Appendix Code
- Console program for approximate roots using Babylonian method
- Hidden Comments Section
Preface
gold Here are some TCL calculations on Babylonian number series.
Introduction
One tablet AO6484 in the Louvre Museum gives a method for finding the sum of a "ladder" (geometric series?). From 1 to 10, sum the powers (literally the "ladder") of 2. The last term you add is 8_32 or decimal 512. Subtract 1 from 8_32, obtaining 8_31. Add 8_31 to 8_32, obtaining the answer 17_3 or decimal 1023. modern formula = 2**n+2**(n-1). There is uncertaincy in the math term "ladder or stair", since 512 is 2**9 (rather than 2**10 as 1024).
One tablet gives a method for finding the sum of a quadratic series. Add the squares from 1 to 10, the last term is 100. The answer is 6_25 in base 60 or decimal 385. The modern formula is (1/3+( 2/3 )*n)*k
One tablet showed a method for finding an approximate square root, using sqrt(a**2 + b) ~=~ a + b/(2*a). As the eTCL console program developed, a**2 was the highest square below the rational number N1, and b was N1-a**2. The eTCL solution is essentially a one pass solution, not an iterative solution. The error in the square root was about 0.38 percent. The square root method was modified for the cube root using b/(3*a) and the error in the cube root was about 8 percent. The console program for babylonian algorithm for roots follows the probable tablet methods, but not very accurate in one pass. An iterative solution is found in Square Root.
For the first testcase, the first term is 1, final term is 100, sum is 385. For the second testcase, the final term is 100.For the third testcase, the final term is 55.
Following series were not proven known to Babylonians or Babylonian notation
Testcase 4. The fourth testcase is 8 terms of the geometric sequence <1 2 4 8 16 32 64 128> with r=2. Given the formula for the nth term, the 8th term is a(1)*r**(n-1), 1*2**(8-1),2**7,128. The sum formula is a(1)*(r**n)-a(1)/ (r-1), substituting (1*(2**8)-1))/(2-1), (2**8-1)/1, 255. Procedure add gives 255, see below.
Testcase 5. The fifth testcase is 12 terms of the geometric sequence <1 2 4 8 16 32 64 128 256 512 1024 2048> with r=2. The 12th term is a(1)*r**(n-1), 1*2**(12-1),2**11,2048. The sum formula is a(1)*r**n-a(1)/ (r-1), substituting (1*(2**12)-1/(2-1),(2**12)-1))/(2-1), (2**12-1)/1, 4096-1, 4095. Procedure add gives 4095, see below.
Testcase 6. The sixth testcase is 4 terms of the geometric sequence <1 2 4 8 > with r=2.. The 4th term from formula is a(1)*r**(n-1), 1*2**(4-1),2**3, 8. The sum formula is a(1)*r**n-a(1)/ (r-1), substituting (1*(2**4)-1/(2-1),(2**4)-1))/(2-1), (2**4-1)/1, 16-1, 15. Procedure add gives 15, see below.
Testcase 7. The seventh testcase is 4 terms of the quadratic sequence <1 4 9 16 > with r=2. The 4th term from formula is a(1)*r**4, 16. The sum formula is a(1)*r**n-a(1)/ (r-1), substituting 1/(n-1)+(2/3)*nth_term*sum (1 2 3 4),(2/3)*16*10 ,30. Procedure add gives 30, see below.
Testcase 8. The 8th testcase is 10 terms of the quadratic sequence <1 4 9 16 25 36 49 64 81 100 > . The 10th term from formula is a(1)*n**2,1.*10**2, 100. The quadratic sequence formula is substituted as ((1/(3))+(2/3)*n)*sum (1 2 3 ... 10),(1/3+(2/3)*10))*55 ,385. Procedure add gives 385, see below.
Testcase 9. The 9th testcase is 4 terms of the quadratic sequence <1 4 9 16 > . The fourth term from formula is a(1)*n**2,1.*4**2, 16. The quadratic sequence formula is substituted as ((1/(rx+1))+(2/(rx+1))*n)*sum (1 2 3 4),(1/3+(2/3)*4))*10 ,30. Procedure add gives 30, see below.
Testcase 10. The 10th testcase is 4 terms of the quadratic sequence <1 4 9 16 > . The fourth term from formula is a(1)*n**2,1.*4**2, 16. The quadratic sequence formula is substituted as ((1/(rx+1))+(2/(rx+1))*n)*sum (1 2 3 4),(1/3+(2/3)*4))*10 ,30. Procedure add gives 30, see below.
Testcase 11. The 11th testcase is 10 terms of the Archimedes sequence <1./1. + 1./4. + 1./16.+ 1./64. + 1./256.+ 1./125.+ 1./1024. + 1./4096.+1/16384.+1./65536. > with r=4 and terms (1/a*4**n. The fourth term from formula is 1./(4**2), 1./16. The Archimedes sequence formula is substituted as (a1*(r**n)-a1)/(r-1),(1.*(1/4)**4)-1.)/(4.-1.), ~4/3. Addition in the eTCL console gives 1.341.
Testcase 12. The 12th testcase is 10 terms of the harmonic series <1./1. + 1./2. + 1./3. + 1./4. + 1./5.+ 1./6.+ 1./7. + 1./8.+ 1./9.+ 1./10.> with r=1 and terms (1/n). The fourth term from formula is 1./n, 1./4. Addition in the eTCL console gives 2.5956 for ten terms.
Testcase 13. The 13th testcase is 10 terms of the alternating harmonic series <1./1. - 1./2. + 1./3. - 1./4. + 1./5.- 1./6.+ 1./7. - 1./8.+ 1./9.- 1./10.> with r=1 and terms (1/n). The fourth term from formula is ( (-1.)**(n+1))/4. Addition in the eTCL console gives 2.5956 for ten terms.
Testcase 14. The 14th testcase is 10 terms of the Euler series <1./1. + 1./2. + 1./9. + 1./16. + 1./25. + 1./32.+ 1./64.+ 1./49. + 1./81.+ 1./100.> with r=1 and terms (1/n). The fourth term from formula is 1/n*n, 1/(4*4), 1/16. Addition in the eTCL console gives 1.8032 for ten terms.
Testcase 15. The modern formula for consecutive integers is formula (1-r**n)/(1-r) = 1+r+r**2+r**3+f**4... +r**n.
Broken Reed Problem
tick of 12 integer units, subtract 1, Add length measurements 12, 12-1, 12-2, 12-3, 12-4,12-5,12-6, 12-7, 12-8, 12-9,12-10, 12-11. Problem setup seems similar to syntax mas ba.si.1.la used as interest cube 1 minus or quantity cube 1 minus . Continuing, quantity square 1 minus might be quantity n*(n-1). Quantity square 2 minus might be quantity n*(n-2).
(n*(n+1))/2 (12*(12+1))/2 12 11 10 9 8 7 6 5 4 3 2 1 [add 12 11 10 9 8 7 6 5 4 3 2 1 ] # answer 78
# following statements can be pasted into eTCL console
proc add {args} {return [ ::tcl::mathop::+ 0. {*}$args]} #
add 1 2 4 8 16 32 64 128 # answer 255
add 1 2 4 8 16 32 64 128 256 512 1024 2048 # answer 4095.0
add 1 2 4 8 # answer 15.0
add 1 4 9 16 # answer 30.0
set babylonian_sequence [ add 1 4 9 16 25 36 49 64 81 100 ] # answer 385.0
set babylonian_problem_formula [expr (1./3. + 2./3.*10.)* 55 ] # answer 384.9999 ~~> 385.
set babylonian_follow_on [expr (1./3.+(2./3.)*4.)*10. ] # answer 30.0
set archimedes_follow_on [expr 1./1. + 1./4. + 1./16.+ 1./64. + 1./256.+ 1./125.+ 1./1024. + 1./4096.+1/16384.+1./65536. ] # answer 1.3413
set harmonic_eval_10_terms [expr 1./1. + 1./2.+ 1./3. + 1./4. + 1./5.+ 1./6.+ 1./7. + 1./8.+ 1./9.+ 1./10.] # 2.928
set alternating_harmonic_eval_10_terms [expr 1./1. - 1./2. + 1./3. - 1./4. + 1./5.- 1./6.+ 1./7. - 1./8.+ 1./9.- 1./10.] # 0.645,
set euler_series_10_terms [expr 1./1. + 1./2. + 1./9. + 1./16. + 1./25. + 1./32.+ 1./64.+ 1./49. + 1./81.+ 1./100.] # answer 1.8032 proc add {args} {return [ ::tcl::mathop::+ 0. {*}$args]} #
add 1 2 4 8 16 32 64 128 # answer 255
add 1 2 4 8 16 32 64 128 256 512 1024 2048 # answer 4095.0
add 1 2 4 8 # answer 15.0
add 1 4 9 16 # answer 30.0
set babylonian_sequence [ add 1 4 9 16 25 36 49 64 81 100 ] # answer 385.0
set babylonian_problem_formula [expr (1./3. + 2./3.*10.)* 55 ] # answer 384.9999 ~~> 385.
set babylonian_follow_on [expr (1./3.+(2./3.)*4.)*10. ] # answer 30.0set archimedes_follow_on [expr 1./1. + 1./4. + 1./16.+ 1./64. + 1./256.+ 1./125.+ 1./1024. + 1./4096.+1/16384.+1./65536. ] # answer 1.3413 set harmonic_eval_10_terms [expr 1./1. + 1./2.+ 1./3. + 1./4. + 1./5.+ 1./6.+ 1./7. + 1./8.+ 1./9.+ 1./10.] # 2.928 set alternating_harmonic_eval_10_terms [expr 1./1. - 1./2. + 1./3. - 1./4. + 1./5.- 1./6.+ 1./7. - 1./8.+ 1./9.- 1./10.] # 0.645, set euler_series_10_terms [expr 1./1. + 1./2. + 1./9. + 1./16. + 1./25. + 1./32.+ 1./64.+ 1./49. + 1./81.+ 1./100.] # answer 1.8032
set sqrt_error [* 100. [- 1. [/ 3.1666666666666665 3.1622776601683795]] ] # 0.3879257199 percent error
set cubert_error [* 100. [- 1. [/ 2.3333333333333335 2.154434690031884]]] # 8.30 percent error
# program finds highest square below rational number, for initial guess of square root
proc list2 { aa bb} { for {set i 1} {[* [+ $i 1] [+ $i 1] ]<=[- $bb 1]} {incr i} {set j 1 };return $i}
list2 1 100 #answer 9 , 9*9 = 81 < 100
# program finds highest cube below rational number, for initial guess of cube root
proc list3 { aa bb} { for {set i 1} {[* [+ $i 1] [+ $i 1] [+ $i 1] ]<=[- $bb 1]} {incr i} {set j 1 };return $i}
[list3 1 100] #answer 4 , 4*4*4=64 < 100
# list squares
proc listsq { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend booboo [ * $i $i 1. ] };return $booboo}
[listsq 1 5]
#answer 1.0 4.0 9.0 16.0 25.0
proc listnumbers { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend booboo [ expr 1.* $i] };return $booboo}
#returns list of integer numbers from aa to bb as reals with decimals, usage listnumbers 1 5
[listnumbers 1 5]
# answer is 1.0 2.0 3.0 4.0 5.0
proc sumsquares5 x {expr {$x<2? 1: $x*$x+[sumsquares5 [incr x -1]]}}
# usage sumsquares5 2 # answer 5
proc sum_ladder x {expr {$x<1? 1: 2**$x+[sum_ladder [incr x -1]]}}
# usage sum_ladder 2 # answer 7 = 2**0+2**1+2**2# following statements can be pasted into eTCL console set project 1.0 set sum_of_squares [ expr 1*1+2*2+3*3+4*4+5*5+6*6+7*7+8*8+9*9+10*10 ] # answer 385 set sum_of_squares [ expr 5*5+6*6+7*7+8*8+9*9+10*10 ] # answer 355 set sum_of_squares [ expr 2*2+3*3+4*4+5*5 ] # answer 54 set sum_of_squares [ expr 1*1+2*2+3*3+4*4+5*5+6*6+7*7+8*8+9*9+10*10+11*11+12*12+13*13+14*14+15*15 ] # answer 1240 set sum_of_2_powers [ expr 1**1+2**2+3**2+4**2+5**2+6**2+7**2+8**2+9**2+10**2]
Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
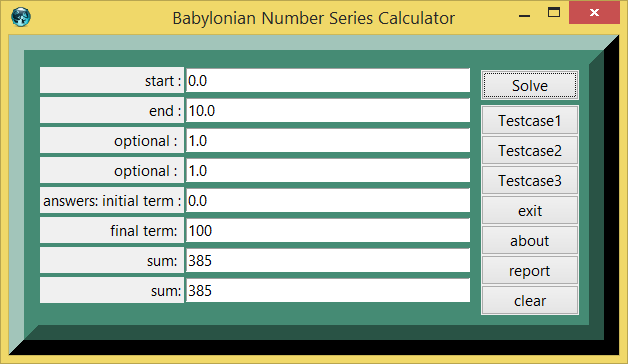
Testcase 1
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 0.0 : | start | |
| 10.0 : | end | |
| 1.0 : | optional | |
| 1.0 : | optional | |
| 0.0 : | answers: initial term | |
| 100 : | final term | |
| 385 : | sum | |
| 385 : | sum |
Testcase 2
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 2.0 : | start | |
| 5.0 : | end | |
| 1.0 : | optional | |
| 1.0 : | optional | |
| 1.0 : | answers: initial term | |
| 25 : | final term | |
| 54 : | sum | |
| 54 : | sum |
Testcase 3
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 0.0 : | start | |
| 15.0 : | end | |
| 1.0 : | optional | |
| 1.0 : | optional | |
| 1.0 : | answers: initial term | |
| 225 : | final term | |
| 1240 : | sum | |
| 1240 : | sum |
Screenshots Section
figure 1.
References:
- goggle "Babylonian Number cuneiform Series"
- Oneliner's Pie in the Sky
- One Liners
- google < Babylonian Interest Rates Wikipedia >
- Ancient Babylonian Algorithms, Donald E. Knuth, Stanford University
- The oldest example of compound interest in Sumer, seventh power of four thirds (4/3)**7 , Kazuo MUROI
- Interest, Price, and Profit: An Overview of Mathematical Economics in YBC 46981,
- Robert Middeke-Conlin Christine Proust, CNRS and Université Paris Diderot
- Compound Interest Doubling Time Rule: Extensions and Examples from Antiquities,
- Saad Taha Bakir, ISSN: 2241 - 1968 (print), 2241 – 195X (online)
- Two Sumerian Words of Fractions in Babylonian Mathematics: igi-n-gál and igi-te-en , Kazuo MUROI
- O. Neugebauer and A. Sachs, Mathematical Cuneiform Texts, American Oriental Society, Series 29. New Haven, 1945.
- K. Muroi, Interest Calculation in Babylonian Mathematics:
- New Interpretations of VAT 8521 and VAT 8528, Historia Scientiarum, 39, (1990), 29-34
- O. Nuegebauer, The Exact Sciences in Antiquity, Second edition, Dover Publication Inc., New York, 1969
- Square Root , Keith Vetter
- A little slide-rule
- What if you do not have exp()?
- Category Algorithm
- A Remarkable Collection of Babylonian Mathematical Texts, Joran Friberg, 2007
- Chalmers University of Technology Gothenburg, Sweden
Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# Babylonian Number Series calculator
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI, 15dec2016
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {start :} }
lappend names {end :}
lappend names {optional : }
lappend names {optional : }
lappend names {answers: initial term :}
lappend names {final term: }
lappend names {sum: }
lappend names {sum:}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Babylonian Number Series
from TCL WIKI,
written on eTCL "
tk_messageBox -title "About" -message $msg }
proc sum_function { start end } {
global side1 side2 side3 side4 side5
global side6 side7 side8
set sum 0
set counter 1
set start [int $start ]
set counter [int $start ]
set end [int $end ]
while { $counter < 1E6 } {
set sum [+ $sum [* $counter $counter ]]
if { $counter < $start } {set side5 [* $counter $counter ] }
set side6 [* $counter $counter ]
if { $counter > [- $end 1. ] } { break}
incr counter
}
return $sum }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set start $side1
set end $side2
set sum_of_squares [sum_function $start $end ]
set side7 $sum_of_squares
set side8 $sum_of_squares
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
console show;
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |&"
puts "&| $side1 :|start| |&"
puts "&| $side2 :|end | |& "
puts "&| $side3 :|optional | |& "
puts "&| $side4 :|optional | |&"
puts "&| $side5 :|answers: initial term | |&"
puts "&| $side6 :|final term | |&"
puts "&| $side7 :|sum | |&"
puts "&| $side8 :|sum | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 0.0 10. 1.0 1.0 0.0 100. 385 385}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 2.0 5.0 1.0 1.0 1.0 25. 55. 55. }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 0.0 15. 1.0 1.0 1.0 225 1240 1240 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Babylonian Number Series Calculator" Console program for approximate roots using Babylonian method
# autoindent from ased editor
# console program for babylonian algorithm for roots.
# follows tablet formulas but not very accurate
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# TCL WIKI , 12dec2016
console show
package require math::numtheory
#namespace path {math::numtheory}
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
proc square_root_function { number_for_root } {
set counter 0
while { $counter < 50. } {
if { [* $counter $counter 1. ] > [* $number_for_root 1.] } {break}
incr counter
}
set starter [- $counter 1 ]
set remainder [* $starter $starter 1. ]
set remainder [- $number_for_root [* $starter $starter 1. ] ]
set square_root_estimate [+ $starter [/ $remainder [* 2. $starter ]]]
}
proc cube_root_function { number_for_root } {
set counter 0
while { $counter < 50. } {
if { [* $counter $counter $counter 1. ] > [* $number_for_root 1.] } {break}
incr counter
}
set starter [- $counter 1 ]
set remainder [* $starter $starter $starter 1. ]
set remainder [- $number_for_root [* $starter $starter $starter 1. ] ]
set square_root_estimate [+ $starter [/ $remainder [* 3. $starter ]]]
}
puts " [square_root_function 10 ] "
puts " [cube_root_function 10 ] "Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
pseudocode for interest rate problem
Babylonian problem: if the interest is, 18 (modern notation= n · n · (n – 1) with n = 3), then the initial capital is 1_30 , decimal 90. Appears to be table lookup problem.
# pseudocode for interest rate problem
pay_back / (capital+rate annual)= debt ratio
debt ratio = (capital+rate)**years
debt ratio = 4/3 ** years
7.5= (4/3)**7
debt ratio = (1+18/60)**years
debt ratio = (1+n · n · (n – 1)/60 )**years , where n evaled at 3
debt ratio = [expr (1.+(18./60.))**3]=2.1, amount doubles in ~2 years
table lookup vs modern formula A=P*((1+i)**n)
maybe the some extant tables are interest rate tables, but not recognised.
possible format for tablet thinking for sum of integers
sum (1 ,2,3 ... 10) = (1/2) * 10 * (10 + 1)
set sum_of_integers [expr (1./2.) * 10. * (10. + 1.) ] # answer 55
A = P + I
A = (1+12/60) + I
A = (1+12/60) +18/60 = 1+30/60gold12dec2018. Removed copyright