Babylonian Cubic Equation Problem and eTCL demo example calculator, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks,gold 12dec2018
Babylonian Cubic Equation Problem and eTCL demo example calculator, numerical analysis
- Babylonian Cubic Equation Problem and eTCL demo example calculator, numerical analysis
- Preface
- Introduction
- Babylonian Cubic Equations into TCL
- Analogs to Volume of Boxes and Triangular Pyramids
- Conclusions
- Conclusions*
- Pseudocode for Babylonian style method in eTCL calculator
- Testcases Section
- Screenshots Section
- References:
- Appendix Code
- One Liner Procedures for Decimal Equivalent to some Babylonian tables
- Trial Derivation for Square Pyramid Volume
- Console Program for Square Root, based on Newton's method from Square Root
- Comments Section
Preface
gold Here are TCL calculations for Babylonian Cubic Equation Problems.
Introduction
In the cuneiform math problems and coefficient lists on clay tablets, there are coefficient numbers which were used in determining the amount of materials and the daily work rates of the workers. In most cases, the math problem is how the coefficient was used in estimating materials, work rates, and math problems. One difficulty is determining the effective magnitude or power of the number coefficient in the base 60 notation. In cuneiform, numbers in base 60 are written using a relative notation. For example, 20 could represent either 20*3600,20,20/60, 20/3600, or even 1/20. The basic dimensions and final tallies were presented in the cuneiform accounts on clay tablets, but some calculations, some units, and some problem answers (aw shucks!) were left off the tablet. Successive or iterated math solutions are called algorithms and the Babylonian methods are some of the earliest algorithms documented circa 1600 BCE. The TCL procedures are descendants of this idea. The Babylonians did not use algebra notation, decimal notation, or modern units, so the reader will have to bear some anachronisms in the TCL code. At least one approach for the modern reader and using modern terminology is to develop the implied algebraic equations and decimal equivalents from the cuneiform numbers. Then the TCL calculator can be run over a number of testcases to validate the algebraic equations.
Babylonian Cubic Equations into TCL
Based on the Friberg discussion of tablet, the Babylonian algorithm for a cubic equation was loaded into an eTCL calculator. The Babylonians did not use algebra notation, so the reader will have to bear some anachronisms in the eTCL pseudocode. The tablet has a set of line by line calculations which effectively have functions for the length, front, and depth of a room constrained, multiplied, and rescaled to equal the volume of a room. Taking the length, front, and depth of a room as three constrained functions in the variable a, the product of three functions scale_constant* length(a)* front(a)* depth(a) equals 1 volume unit. For restating the problem in a computer algorithm, the room dimensions will be each in cubits and the volume unit will be in volume sars, 1 volume sar = 144 cubic cubits. In the original problem, the room dimensions were given as 3 different length units and seems unnecessarily complicated. Once the problem is set up, the Babylonians had a lookup table for n*n*(n-1) to solve for the variable a. The eTCL calculator will have to use an iterative solution for the n*n*(n-1) series. The solution from the tablet was length 6, front 4, depth 6, and volume 144 cubits.
Gist. The room dimensions were given as 3 different length units and 2 different volume units, which seems unnecessarily complicated as a calculator algorithm. The solution from the tablet was equivalent length 6 cubits, front 4 cubits, depth 6 cubits, and volume 144 cubic cubits. The Babylonians were looking for solutions using integers only. In the original Babylonian set up for the cubic problem, there may be some problems that do not have an satisfactory integer solution, only the nearest integer solution. The TCL calculator uses real decimal numbers. The tablet solution was equilvalent to { 6*4*6 } = 144 cubic cubits.
Some fragmented Babylonian tables known as n*n*(n+1) tables were used in solving some cubic equations, ref Joran Friberg. The equations were of the form n*n*(b*n+1) = c. The eTCL calculator could generate the expected tables of n*n*(n+1).
Other Babylonian tables known as n*(n + 1)*(n + 2) and n*n*(n – 1) tables have been identified, but no abundant use has been cited from the known Babylonian math problems. Although not clear, tables of the n*(n + 1) might have existed. From modern theory, n · (n + 1)/2 = sum of integers (1,2,3,4...) and n*(n + 1)*(n + 2) /6 = sum of squares (1,4,9....). Possibly, the Seleucid math problem used an n*(n + 1)*(n + 2) table. Possibly, the tables for n*(n + 1)*(n + 2) and n*n*(n – 1) could have been used for cubic equations.
The Seleucid method for sum of squares can be factored for sum of integers term and can be restated as a quasi_cube, ((1/3)(1+2 *n) ) * ( n(n+1)/2.) = (1/6)* n(n+1)(2n+1) = (1/6)*quasi_cube term. Another possible form for the quasi_cube (1/6)* n(n+1)(2n+1) with 2 factored out is expression 2*(1/6)* n(n+1)(n+(1/2)) . Problems for sum of squares and sum of rectangles go far back through the Selucid and Old Babylonian math, although Old Babylonian math may not demonstrate complete knowledge.
Modern derivations for sum of integer squares are treating 3 step pyramids as assembled quasi_cube such as 3 * (1, 2,9,16...n**2) = n*(n+1)*(n+1/2); (1, 2,9,16...n**2) = (1/3) (n*(n+1)*(n+1/2)). The volume of the assembled quasi-cube is product of length (n) , width (n+1), and height (n+1/2)
If the quasi-cube n*(n + 1)*(n + 2) is treated as the modern derivations, the volume of the quasi-cube n*(n + 1)*(n + 2) is product of length (n) , width (n+1), and height (n+2). Then 3*expression = n*(n+1)*(n+2); expression = (1/3)*n*(n+1)*(n+2) . If the eTCL calculator is loaded for testcase 4 with depth n+2 at the window and front n+1 in the internal code, there is a solution at l*f*d of 6*5*7 =209 cubic cubits. Kind of a circular argument, but one problem VAT 6599 # 23 from Friberg has solution of l*f*d of 6*6*7 = 252 cubic cubits. If the depth of the cellar problem is modeled as (n+2), then the depth should be deeper than the normal (n+1) constraint. Using proportions, depth of 6*((n+2)/(n+1)), 6*((6+2)/(6+1)) = 6.857 cubits, close to integer 7. Using proportions, front of 6*((n+1)/(n+2)), 6*((6+1)/(6+2)) = 5.25 cubits. Maybe, the problems with extended cellars (usually deeper by 1 cubit) are tracking with quasi-cube n*(n + 1)*(n + 2). Some proportional scheme or gaming with crt(volume)*((n+2)/(n+1)) or crt(volume)*((n+1)/(n+2))''' is also possible. The Babylonian solutions on the tablets are effectively integer cubits, not the digital cubits the eTCL calculator throws out.
Analogs to Volume of Boxes and Triangular Pyramids
A clay tablet for solving cubic equations has found, probably from ancient city of Larsa, Sumer, Modern Iraq, BCE 2000. For the first entry values 1 to 30, the second value on the clay tablet equals { n*(n+1)*(n+2) }. The modern Tetrahedral formula in TCL notation as expr {($n*($n+1)*($n+2))/6. } can be proportional and related to the volume of a triangular pyramid using the $n expressions as linear dimensions. Treat the $n expressions as linear dimensions < width = $n> *< length = ($n+1)>* < height = ($n+2) >. The assignment of n and (n+1) to respective width and length is arbitrary, but does seem to track with a limited set of problems. A box or cellar would have a volume of <width= $n> *< length = ($n+1)> * < height = ($n+2) >. The volume of a triangular pyramid is (1/3) * ( base_area ) * height. Subbing a right triangle as base for the triangular pyramid, the volume is (1/3) * ( 1/2 ) * width * length * height. The volume of this triangular pyramid with a triangular base is (1/3) * ( 1/2 ) *<width= $n> *< length = ($n+1)> * < height = ($n+2) >. The volume of the cellar is equivalent to the same volume of 6 triangular pyramids with triangular bases of the given dimensions.
The volume of a triangular pyramid is (1/3) * ( base_area ) * height. Subbing a square or rectangle as base for the triangular pyramid, the volume is (1/3) * width * length* height. Continuing in a similar manner, the volume of this triangular pyramid with a rectangular base is (1/3) *<width= $n> *< length = ($n+1)> * < height = ($n+2) >. The volume of the cellar is equivalent to the same volume of 3 triangular pyramids with rectangular bases of the given dimensions.
proc tetrahedral_TETN { n } { return [expr {($n*($n+1)*($n+2))/6. } ]}Conclusions
The Babylonians did not have modern algebra notation, general notation for negative numbers, or a general solution to cubic equations. In the available problem translations, there are several mathematical techniques which were used to handle cubic problems or problems in three dimensions. The documented techniques are 1) finding coefficients or functions of the three dimensions, usually a constant times length, 2) scaling technique to reduce coefficient to unity, 3) substitution and resetting dimensions, including table look up.
Some fragmented Babylonian tables known as n*n*(n+1) tables were used in solving some cubic equations, ref Joran Friberg. The implied modern equations were of the form n*n*(b*n+1) = c. The eTCL calculator could generate the expected tables of n*n*(n+1). Other Babylonian tables known as n*(n + 1)*(n + 2) and n*n*(n – 1) tables have been identified, but no abundant use has been cited from the known Babylonian math problems. Although not clear, tables of the n*(n + 1) might have existed. From modern theory, n · (n + 1)/2 = sum of integers (1,2,3,4...) and n*(n + 1)*(n + 2) /6 = sum of squares (1,4,9....). Possibly, the Seleucid math problem used an n*(n + 1)*(n + 2) table. Possibly, the tables for n*(n + 1)*(n + 2) and n*n*(n – 1) could have been used for cubic equations. The Seleucid method for sum of squares can be factored for sum of integers term and can be restated as a quasi_cube, ((1/3)(1+2 *n) ) * ( n(n+1)/2.) = (1/6)* n(n+1)(2n+1) = (1/6)*quasi_cube term. Another possible form for the quasi_cube (1/6)* n(n+1)(2n+1) with 2 factored out is expression 2*(1/6)* n(n+1)(n+(1/2)) . Problems for sum of squares and sum of rectangles go far back through the Selucid and Old Babylonian math, although Old Babylonian math may not demonstrate complete knowledge. At least in referring to TCL procs, the Babylonian table known as n*(n + 1)*(n + 2) is not that far from the sum of squares and triangular numbers as n*(n + 1)*(n + 2)/6.
Conclusions*
Overall, the Babylonian mathematical tables, particularly the nn(n+1) tables, were instrumental in solving cubic equations during ancient times. By using tools like the eTCL calculator to generate these tables, we can better understand how the Babylonians approached such mathematical problems. Additionally, further research into other Babylonian tables, such as the n*(n + 1)(n + 2) and nn*(n – 1) tables, may uncover more applications in solving cubic equations. Studying these ancient mathematical techniques provides valuable insights into the early development of mathematical concepts and problem-solving methods.
Pseudocode for Babylonian style method in eTCL calculator
# using pseudocode for Babylonian style methods and table lookup (eg. cubic problems )
# possible problem instances include separate tables for cubes n*n*n and quasi_cubes
quasi_cube n*n*(n-1), quasi_cube n*(n + 1)*(n + 2),
quasi_cube n*n*(n + 1), quasi_square n*(n+1)
cube proportions of length : front : depth could be set like
1:1:1, 1:(1/2):1, 1:(2/3):1 4:(1/4):1,
testcase 1 has l/f/h as 1*a:(2/3)*a:(12*a+1)
testcase 1 has quasi_cube n*n*(n - 1) as model
depth = front ; length = depth ; cube_volume = 216
length(1*a)*front(1*a)*depth(1*a) =216 cubic cubits
set table_look_up = cube root 216
set table_look_up = [** 216 [/ 1. 3. ]] = [** $cube_volume [/ 1. 3. ]]
set a $table_look_up ;
if {quasi_cubes } { find iterative [* $n $n [- $n 1. ]] };
set length [* 1. $a ] ; set front [* 1. $a ] ; set depth [* 1. $a ]
set check_answer $length*$front*$depth =? cube_volume (yes/no?) # using pseudocode for quasi_cube n*(n + 1)*(n + 2), with Babylonian style methods.
set cube_root [expr 252**(1./3.) ] #= 6.3163
set n [int [expr $volume**(1./3.) ]] #= 6
set factor_front [expr 6.3163*((6.3163+1.)/(6.3163+2.)) ] #= 5.5567
set factor_depth [expr 6.3163*((6.3163+2.)/(6.3163+1.)) ] #= 7.1796
set check_product [* 6.3163 5.5567 7.1796 ] #=251.9880
set factor_front [expr $ n*(($n+1.)/$n+2.))
set factor_depth [expr $n *(($n+2.)/($n+1.))
set quasi_cube [expr $n*($n + 1.)*($n + 2.) ] #= n= 6.3163, quasi_cube=384.3124
set integer [expr $n*($n + 1.)*($n + 2.) ] #= n= 6, quasi_cube=336.0
set check_answer [* [round 6.3163 ] [round 5.5567] [round 7.1796 ]]
#= gives check_answer of 252
integer solution would be l/f/d = 6/5/7 cubits, [* 6 5 7 ]= 210Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
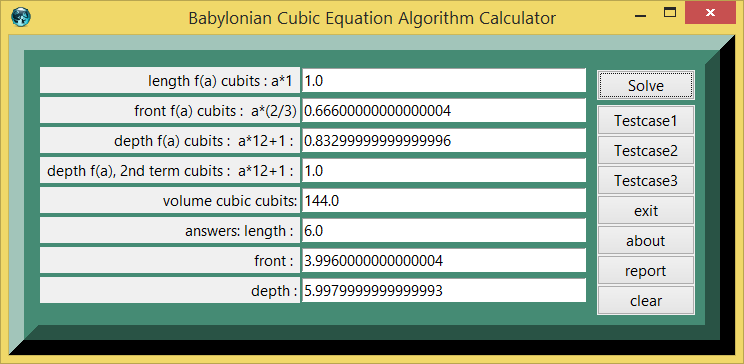
Testcase 1
| table 1 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 1.0 : | length cubits | |
| 0.666 : | front cubits | |
| 0.832 : | depth cubits | |
| 1.0 : | depth 2nd term cubits | |
| 144.0 : | volume cubic cubits: | |
| 180 : | volume limit table look up: | |
| 6 : | table look up solution: | |
| 143.808 : | check; product length*front*depth =? vol : | |
| 6.0 : | length cubits | |
| 3.996 : | front cubits | |
| 5.997 : | depth cubits |
Testcase 2
| table 2 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 1.0 : | length cubits | |
| 0.666 : | front cubits | |
| 0.8329 : | depth cubits | |
| 1.0 : | depth 2nd term cubits | |
| 200.0 : | volume cubic cubits: | |
| 294 : | volume limit table look up: | |
| 7 : | table look up solution: | |
| 222.922 : | check; product length*front*depth =? vol : | |
| 7.0 : | length cubits | |
| 4.6619 : | front cubits | |
| 6.8309 : | depth cubits |
Testcase 3
| table 3 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 1.0 : | length cubits | |
| 0.666 : | front cubits | |
| 0.8329 : | depth cubits | |
| 1.0 : | depth 2nd term cubits | |
| 300.0 : | volume cubic cubits: | |
| 448 : | volume limit table look up: | |
| 8 : | table look up solution: | |
| 326.670 : | check; product length*front*depth =? vol : | |
| 8.0 : | length cubits | |
| 5.328 : | front cubits | |
| 7.6639 : | depth cubits |
Testcase 4
| table 4 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 4: | testcase_number | |
| 1.0 : | length cubits | |
| 0.666 : | front cubits | (n+1) increase from normal code |
| 0.8329 : | depth cubits | |
| 2.0 : | depth 2nd term cubits | (n+2) increase from normal value |
| 144.0 : | volume cubic cubits: | |
| 180 : | volume limit table look up: | |
| 6 : | table look up solution: | |
| 209.772 : | check; product length*front*depth =? vol : | |
| 6.0 : | length cubits | |
| 4.996 : | front cubits | |
| 6.997 : | depth cubits | (n+2) proportional increase from normal |
Screenshots Section
figure 1.
figure 2.
Babylonian Cubic Equation Problem EQUILATERAL TRIANGLE PNG
References:
- Oneliner's Pie in the Sky
- One Liners
- Category Algorithm
- Brahmagupta Area of Cyclic Quadrilateral and eTCL demo example calculator
- Gauss Approximate Number of Primes and eTCL demo example calculator
- goggle "Babylonian Number cuneiform Series"
- Oneliner's Pie in the Sky
- One Liners
- google < Babylonian Interest Rates Wikipedia >
- Ancient Babylonian Algorithms, Donald E. Knuth, Stanford University
- The oldest example of compound interest in Sumer, seventh power of four thirds (4/3)**7 , Kazuo MUROI
- Interest, Price, and Profit: An Overview of Mathematical Economics in YBC 46981,
- Robert Middeke-Conlin Christine Proust, CNRS and Université Paris Diderot
- Compound Interest Doubling Time Rule: Extensions and Examples from Antiquities,
- Saad Taha Bakir, ISSN: 2241 - 1968 (print), 2241 – 195X (online)
- Two Sumerian Words of Fractions in Babylonian Mathematics: igi-n-gál and igi-te-en , Kazuo MUROI
- O. Neugebauer and A. Sachs, Mathematical Cuneiform Texts, American Oriental Society, Series 29. New Haven, 1945.
- K. Muroi, Interest Calculation in Babylonian Mathematics:
- New Interpretations of VAT 8521 and VAT 8528, Historia Scientiarum, 39, (1990), 29-34
- O. Nuegebauer, The Exact Sciences in Antiquity, Second edition, Dover Publication Inc., New York, 1969
- Mathematical Treasure: Old Babylonian Area Calculation, uses ancient method
- Frank J. Swetz , Pennsylvania State University
- Wikipedia, see temple of Edfu, area method used as late as 200 BC in Egypt.
- Hoyrup, Jens (1992), "The Babylonian Cellar Text BM 85200 + VAT 6599 Retranslation and Analysis"
- Square Root , Keith Vetter
- A little slide-rule
- What if you do not have exp()?
- Category Algorithm
- A Remarkable Collection of Babylonian Mathematical Texts, Joran Friberg, 2007
- Chalmers University of Technology Gothenburg, Sweden
- Babylonian Mathematics, cubic equations, Don Allen, Texas A&M University
- Minna Burgess Connor, A historical survey of methods of solving cubic equations, master's thesis, 7-1-1956
- Crossley, John; W.-C. Lun, Anthony (1999). The Nine Chapters on the Mathematical Art: Companion and Commentary. Oxford University Press.
- Land surveying in ancient Mesopotamia, M. A. R. Cooper
Appendix Code
appendix TCL programs and scripts
# TCL source code follows
# pretty print from autoindent and ased editor
# Babylonian Cubic Equation Algorithm V2
# written on Windows XP on TCL
# working under TCL version 8.6
# gold on TCL Club, 12Dec2018
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} { length f(a) cubits : a*1 } }
lappend names { front f(a) cubits : a*(2/3)}
lappend names { depth f(a) cubits : a*12+1 : }
lappend names { depth f(a), 2nd term cubits : a*12+1 : }
lappend names { volume cubic cubits:}
lappend names {answers: length : }
lappend names {front : }
lappend names {depth :}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Babylonian Cubic Equation Algorithm V2
# gold on TCL Club, 12Dec2018 "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg " Babylonian Cubic Equation Algorithm V2
from TCL ,
# self help listing
# problem, Babylonian Cubic Equation Algorithm V2
# 5 givens follow.
1) length f(a) cubits : a*1
2) front f(a) cubits : a*(2/3)
3) depth f(a) cubits : a*12+1
4) depth f(a), 2nd term cubits : a*12+1
5) volume cubic cubits:
# Recommended procedure is push testcase and fill frame,
# change first three entries etc, push solve,
# and then push report. Report allows copy and paste
# from console to conventional texteditor. For testcases
# testcase number is internal to the calculator and
# will not be printed until the report button is pushed
# for the current result numbers.
# >>> copyright notice <<<
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK license terms.
# Editorial rights and disclaimers
# retained under the TCL/TK license terms
# and will be defended as necessary in court.
Conventional text editor formulas or grabbed from internet
screens can be pasted into green console.
# gold on TCL Club, 12Dec2018 "
tk_messageBox -title "Self_Help" -message $msg }
proc table_look_up {limit } {
global look_up_function counter
set counter 1
while { $counter < 50. } {
set look_up_function [* $counter $counter [- $counter 1] ]
if { [* $counter $counter [- $counter 1] ] > [* $limit] } {return $counter ; break}
incr counter
}
}
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global look_up_function counter check_product_lfd
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
# initialize hard wired solution
set a 6.
set room_volume $side5
set a [ table_look_up $room_volume ]
set room_volume [expr ($a*$side1)*($a*$side2)*($a*$side3+$side4) ]
set length [expr $a*$side1 ]
set front [expr $a*$side2 ]
set depth [expr $a*$side3+$side4 ]
set check_product_lfd [* $length $front $depth 1. ]
set side6 $length
set side7 $front
set side8 $depth
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global look_up_function counter check_product_lfd
global testcase_number
console show;
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Babylonian Cubic Equation Report , screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts "%|table $testcase_number|printed in| tcl format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |&"
puts "&| $side1 :|length cubits| |&"
puts "&| $side2 :|front cubits | |& "
puts "&| $side3 :|depth cubits | |& "
puts "&| $side4 :|depth 2nd term cubits | |&"
puts "&| $side5 :|volume cubic cubits: | |&"
puts "&| $look_up_function :|volume limit table look up: | |&"
puts "&| $counter :|table look up solution: | |&"
puts "&| $check_product_lfd :|check; product length*front*depth =? vol : | |&"
puts "&| $side6 :|length cubits | |&"
puts "&| $side7 :|front cubits | |&"
puts "&| $side8 :|depth cubits | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 1.0 0.666 0.833 1. 144.0 6. 4. 6.}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 1.0 0.666 0.833 1.0 200.0 7. 4.6 6.8 }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 1.0 0.666 0.833 1.0 300.0 8. 5.3 7.6 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .self_help -text self_help -command { self_help }
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Babylonian Cubic Equation Algorithm Calculator V2"
# gold on TCL Club, 12Dec2018 Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
One Liner Procedures for Decimal Equivalent to some Babylonian tables
# following one liners are decimal equivalent to some Babylonian tables
# possible cubic problem instances include separate tables for cubes n*n*n and quasi_cubes
# quasi_cube n*n*(n-1), quasi_cube n*(n + 1)*(n + 2), quasi_cube n*n*(n + 1), quasi_square n*(n+1)
# list_integers is list of positive integers, 1 2 3 4 ... n
proc list_integers { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i 1.]};return $boo}
# usage, list_integers 1 10
# 1.0 1.0 2.0 2.0 3.0 3.0 4.0 4.0 5.0 5.0 6.0 6.0 7.0 7.0 8.0 8.0 9.0 9.0 10.0 10.0
# list_reciprocals is list of 1/1 +1/2 1/3 1/4 ... 1/n
proc list_reciprocals { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [/ 1. $i ]};return $boo}
# usage, list_reciprocals 1 10
# 1.0 1.0 2.0 0.5 3.0 0.333 4.0 0.25 5.0 0.2 6.0 0.166 7.0 0.142 8.0 0.125 9.0 0.11 10.0 0.1
# list_squares is list of integer squares,
proc list_squares { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i $i ]};return $boo}
# usage, list_squares 1 10
# 1.0 1 2.0 4 3.0 9 4.0 16 5.0 25 6.0 36 7.0 49 8.0 64 9.0 81 10.0 100
# quasi_cube2 is n*(n)*(n-1)
proc list_quasi_cube2 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i $i [- $i 1]]};return $boo}
# usage, list_quasi_cube2 1 10
# 1.0 0 2.0 4 3.0 18 4.0 48 5.0 100 6.0 180 7.0 294 8.0 448 9.0 648 10.0 900
# quasi_cube3 is n*(n+1)*(n+2)
proc list_quasi_cube3 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i [+ $i 1] [+ $i 2]]};return $boo}
# usage list_quasi_cube3 1 10
# 1.0 6 2.0 24 3.0 60 4.0 120 5.0 210 6.0 336 7.0 504 8.0 720 9.0 990 10.0 1320
# quasi_cube4 is n*(n)*(n+1)
proc list_quasi_cube4 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i $i [+ $i 1]]};return $boo}
# usage, list_quasi_cube4 1 10
# 1.0 2 2.0 12 3.0 36 4.0 80 5.0 150 6.0 252 7.0 392 8.0 576 9.0 810 10.0 1100
# quasi_square2 is n*(n+1),
proc list_quasi_square2 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i [+ $i 1]]};return $boo}
# usage, list_quasi_square2 1 10
# 1.0 2 2.0 6 3.0 12 4.0 20 5.0 30 6.0 42 7.0 56 8.0 72 9.0 90 10.0 110
# list_sum_integers
proc list_sum_integers { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [/ [* $i [+ $i 1] ] 2. ]};return $boo}
# usage, list_sum_integers 1 10
#1.0 1.0 2.0 3.0 3.0 6.0 4.0 10.0 5.0 15.0 6.0 21.0 7.0 28.0 8.0 36.0 9.0 45.0 10.0 55.0
# list_sum_squares
proc list_sum_squares { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [/ [* $i [+ $i 1.] [+ [* $i 2.] 1.]] 6.]};return $boo}
# usage list_sum_squares 1 10
# 1.0 1.0 2.0 5.0 3.0 14.0 4.0 30.0 5.0 55.0 6.0 91.0 7.0 140.0 8.0 204.0 9.0 285.0 10.0 385.0
proc list_babylonian_reciprocal_base_60 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [/ 60. $i] };return $boo}
# usage, list_babylonian_reciprocal_base_60 1 5 , set wosh [ list_babylonian_reciprocal_base_60 1 5 ]
# answer sequence = 1.0 60.0 2.0 30.0 3.0 20.0 4.0 15.0 5.0 12.0
proc list_babylonian_reciprocal_base_12 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [/ 12. $i] };return $boo}
# usage, list_babylonian_reciprocal_base_12 1 5 , set wosh [ list_babylonian_reciprocal_base_12 1 5 ]
# answer sequence = 1.0 12.0 2.0 6.0 3.0 4.0 4.0 3.0 5.0 2.4Quasi-cubes and Quasi-squares in derivation and formulas
western derivation from ( N * (N+1)) table.
2 * 1 = 1 * 2,
2 * (1 + 2) = 2 * 3,
2 * (1 + 2 + … + 10) = 10 * 11.
2* E(1 + 2 + … + N) = N*(N+1)
E(1 + 2 + … + N) = (N*(N+1))/2.
8) E(1,N) =0.5*(N*(N+1)), sum of N numbers from 1 to N
western derivation from (N * N * (N+1)) table
2 * 1 = 1 * 2,
2 * (1 + 2) = 2 * 3
2 * E(1 + 2 + … + 10) = 10 * 11.
N * 2 * E(1 + 2 + … + N) = N * N * (N+1)
E(1 + 2 + … + N) = (N * N * (N+1))/(2*N)
9) E(1 + 2 + … + N) = (N * N * (N+1))/(2*N)
western derivation from (N * N * (N+1) table
(N * N * (N+1) = (N * N * (N+1)
(N * N * (N+1) = N * N * N + N*N
10) (N * N * (N+1) = cube(N) + square(N)
TCL expressions follow
set Quasi-square(N*(N-1), 1, N) [expr { N * (N-1)}]
set Quasi-square(N*(N+1), 1, N) [expr { N * (N+1)}]
set (N * N * (N+1)) [expr { N**3 + N**2 }]
set E(N,1, N) [expr {0.5*(N*(N+1))}]
set E(N,1, N) [expr { (N**3 + N**2)/(2.*N) }]
set Cube(N) [expr { N * N * N }]
set Quasi-cube1(N) [expr { (N * N * (N+1)) } ]
set Quasi-cube2(N) [expr { (N * N * (N-1)) } ]
set Quasi-cube3(N) [ expr { (N * N * (N-2)) } ]
set Quasi-cube4(N) [ expr { (N * (N+1) * (N+2)) } ]
set E( (N*N+1),1,N) [expr { (1./3)*(N * (N+1) * (N+2))}]Babylonian Progression treatment of Squares and Volumes, Maybe split off onto another page.
Trying to boil cuneiform math down to simple phrases. Main reference was "A Remarkable Collection of Babylonian Mathematical Texts" by Joran Friberg. Cuneiform phases use () for understood, not on tablet. Cubes and Quasi-cubes are related to summation theorems. Transliteration: (square) N .e N íb.si8 (tablet phrase). 1) trans. (square) N makes N equalsided (where N is an integer). related terms ib.si8 and sa observed with squares. sa also has observed connotation as rates and coefficients. homophome si (plain) observed with cubes. homophome si8 not observed with strictly cubes. Suggested: (quasi-square) N .e N ib.si.1.la (tablet phrase). 2) poss. trans. (quasi-square ( N * (N-1)) N makes N equalsided. 3) Transliteration: (cube) N N (where N is an integer) (tablet phrase). Transliteration: (cube) N .e N ba.si-tam (tablet phrase). 4) (cube) N makes N likesided (in accusative) (where N is an integer). 5) (quasi-cube) N makes N (accusative) likesided (where N is an integer). Transliteration: (quasi-cube) N .e N ba.si (tablet phrase). 6) trans. (quasi-cube (N * N * (N+1)) N makes N likesided. (where N is an integer, 1 to 60 in table). Either troubling or revealing, phrases for quasi-cube exactly the same. as some cube tables (N*N*N). Suggested: (quasi-cube) N .e N ba.si.1.la (tablet phrase). 7) poss. trans. (quasi-cube (N * N * (N-1)) N makes N likesided. Term ba.si.1.la means “cube-minus-1”. or “cube lacking one” creating a quasi-cube. Analog to Roman numerals, 4 = {IV} , 5 lacking one. Analog to Sumerian cuneiform numerals, 19 = { | << }, 20 lacking one.
From the math problems on tablets, the Babylonian mathematicians did not usually make derivations, axioms, explanations, and propositions for Algebraic formulas and derivations in general terms (N+1,N*N,N*N*N) like the Classic Greek and modern notations. On some Babylonian math tables (not all), there are cuneiform headers and phrases with the numbers listed as squares, cubes, and metrological units. While the terms on the Babylonian square and cube tables are not completely understood here, the analysis will develop some peg points or propositions for the understanding of the extant Babylonian algorithms for the transformation and development of the TCL algorithms. For 2-d geometric figures, squares of sides are proportional to surface area, N*N =oc surface area. For 3-d geometric figures, cubes of sides are proportional to volume, N*N*N =oc volume. The summation E(1+2+3...N) equals (N*(N+1))/2. , which is equivalent to E(N) = 0.5*(N*(N+1)). The summation E(1+2+3...N) equals (N*(N+1))/2.=0.5*(N*(N+1)). The summation E(1+2+3...N) equals (N * N * (N+1))/(2*N). For a 2-d figure of equal sides and substituting, the summation E(1+2+3...N) is proportional to surface area. For a 3-d figure of equal sides and substituting, the summation E(1+2+3...N) is proportional to volume. When a simple N is summed, a factor of 1/2 is involved. When a complex term like (N*N+1) is summed, different integer factors may be involved. For 2-d geometric figures, area may be proportional to 1/2. For 3-d figures, volume may be proportional to 1/3. Some volumes or other expressions of products may be proportional to the product (1/2)*(1/3).
The volume of square pyramid approximates (1/3)*base_area*height or (1/3)*side_base*side_base*height. The volume of rectangular pyramid equals (1/3)*side_base_1*side_base_2*height and substituting expr { (1./3.)* 10. *11.*12.} = 440. Following identities are set by Friberg. Substituting the summation formula, the volume of rectagular pyramid approximates expr {N* (N + 1)) * (N + 2)/3)}. The summation on sum of integers 1 through 10, 2*(1 + 2 + … + 10) equals (10 *11), which can be interpreted as a rectangle of sides 10 and 11 (read as sides N and N+1). Further, (1 + 2 + … + 10) equals .5* (10 *11), which can be interpreted as half a rectangle or triangle of sides 10 and 11 ( read as sides N and N+1) . Restating .5*(N*(N+1)) and multiply height as (N+2) , (1 + 2 + … + N)*(N+2) equals .5*(N*(N+1))*(N+2)), which can be interpreted as a volume of triangular prism 10/11/12. From Euclid, a triangular prism can be divided into three equal sized pyramids. One of these pyramids would be (1/3)*(1 + 2 + … + N)*(N+2) equals expr {(1./3.)*.5*(N*(N+1))*(N+2))}. One pyramid equals expr {(1./3.)*.5*(10*(10+1))*(10+2)}, 220.?
Quote from papyrus on Egyptian_demotic_summation ref P.BM10520 (Parker DMP(1972)). The iterated sum of the integers from 1 to 10, called “1 filled up twice to 10”. The value is calculated either as expr {55 * 12. /3.}, 220 or “filled up twice” as expr {2*55 * 12. /3.}, 440. The probable Egyptian_demotic_summation formula is expr 2*{N* (N + 1)/2} * (N + 2)/3}. Not sure about the Egyptian context and variable manipulation, but expr {2*55*12./3.} or 440 is nearly volume of rectangular pyramid (10/11/12). The possible Egyptian_demotic_summation formula is expr 2*{N* (N + 1)/2} * (N + 2)/3} as volume of rectangular pyramid. The triangular pyramid formula is (1/6.) base_side* apothem *height and substituting expr {(1/6.)* 10.*(1./2.)*11.*sqrt(3)*12.} =190.525. The Egyptian_demotic papyrus BM10520 may be a partial derivation of volume for a square or rectangular pyramid. The sum of integers as 55 for integers 1 through 10 was known on Bablyonian clay tablet. Ref BM 96954 + BM 102366 + SÉ 93 in Friberg, PCHM 6 (1996), Friberg, UL (2005), Fig. 4.8,4, and in Robson, MMTC (1999), Appendix 3. Be very interested if a “myr” was cited on this papyrus BM 10520.
The volume of square pyramid approximates (1/3)*base_area*height or (1/3)*side_base*side_base*height.
Trial Derivation for Square Pyramid Volume
first pyramid slab vol = (B*N/N)*(B*N/N) * H/N , N’th last slab
vol of pyramid slabs (B*1/N)^2 * H/N + (B*2/N)^2 * H/N + ... + (B*N/N)^2 * H/N, ref Dr Math
square pyramid vol = (B/N)^2 * H/N * (1*2 + 2*2 + ...+ N*2), slabs ref SUM OF SQUARES
square pyramid vol = ((n)/N)* ((n+1)/N) * ((n+2)/N) * (1*2 + 2*2 + ...+ N*2)
(1*2 + 2*2 + ...+ N*2) = N*(N + 1)*(2N + 1)/6 = SUM OF SQUARES
N · (N + 1) · (N + 2)/6 = SUM OF SQUARES
{N * (N + 1)/2} * { (N + 2)/3. } = SUM OF INTEGERS * FACTOR (N + 2)/3.
FACTOR = (N/N + 2/N)/3 = (1 + 2/N)/3 = (1/3 + 2/(N*3) = 1/3 , AS N >>> INFINITY
(N · (N + 1) · (N + 2)/6) / N = RATIO FOR SUM OF SQUARES TO N, AS N >>> INFINITY
((1/N) · ((1/N) + 1) · ((1/N) + 2)/6) =
1*(2)/6 =
1/3 = RATIO FOR SUM OF SQUARES TO N, AS N >>> INFINITY
(N * (N + 1)/2) / N RATIO FOR SUM OF INTEGERS TO N, AS N >>> INFINITY
(1 * (1+ 1/N)/2) = 1/2+ 1/(2*N), N>>> INFINITY
1/2 RATIO FOR SUM OF INTEGERS TO N, AS N >>> INFINITYIn the Babylonian clay tablets, there are some progressions of squares and triangles. As discussed by D.A.R. DeSegnac, MAH16055 has diagrammed ten triangles of increasing dimensions ca.1900 - 1600 BC. Some Babylonian progressions have possible uses for metrology, architecture, or generating school geometry problems. The modern derivations of the pyramid volume formula use calculus or progressions to sum geometric wafers or layers to generate the volume formulas for square pyramids and other 3d figures. The ancient Egyptian architecture had stepped pyramids and the Mesopotamian architecture had stepped rectanguloids, so progressions were of great interest to the Babylonian mathematicians. TCl subroutines can generate these square and triangle progressions as lists, metrology tables, sum total areas, and illustrate total possible volume interpretations for study.
References:
- A HARMONY OF NUMBERS by D.A.R. DeSegnac ,
- MAH 16055 ca.1900 - 1600 BC, discussion
- on progression of ten triangles from clay tablet.
##### TCL Source Code follows
# pretty print from autoindent and ased editor
# Triplet progression produced by tablet diagram
# written on Windows XP for TCL Windows Console
# working under TCL version 8.6
# gold on TCL club
package require Tk
package provide calculatorliner 1.0
namespace path {::tcl::mathop ::tcl::mathfunc}
set tclprecision 17
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Babylonian Triplets Report , screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
proc precisionx {precision float} {
# tcl:wiki:Floating-point formatting, [AM]
# select numbers only, not used on every number or subroutine
set x [ expr {round( 10 ** $precision * $float) / (10.0 ** $precision)} ]
# usage rounded or clipped to nearest 5ird significant figure
set x [ format "%#.5g" $x ]
return $x
}
proc list_triplet_sequence { aa bb} {
for {set i 1} {$i<=$bb} {incr i} {
lappend boo [ precisionx 3 [* .1800 [+ 27. [/ 7. 9. ]] $i ]];
lappend boo [ precisionx 3 [* .1800 [+ 22. [/ 2. 9. ]] $i ]];
lappend boo [ precisionx 3 [* .1800 [+ 16. [/ 6. 9. ]] $i ]];}
return $boo}
set triplet_progression [list_triplet_sequence 1 10 ]
puts $triplet_progression
# usage, list_triplet_sequence, set trippy [list_triplet_sequence 1 3 ]
# creates sequence of triplet numbers from cuneiform diagram
# reference D.A.R. DeSegnac, Harmony of Numbers
# discussion of tablet. MAH_16055 ca.1900 - 1600 BC
# answer sequence = 5. 4. 3. 10. 8. 6. 15. 12. 9.
# uses for and lappend statements
# This code is copyrighted same as TCL version 8.6
# 3aug2018 copyrighted under and same as TCL license.
# Editorial rights are reserved under TCL license
# gold on TCL clubConsole Program for Square Root, based on Newton's method from Square Root
# autoindent from ased editor
# console program for babylonian algorithm for roots.
# combined tablet formulas and Newton's method
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# TCL WIKI , 12dec2016
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
proc square_root_function { number_for_root } {
set counter 0
set epsilon .0001
while { $counter < 50. } {
if { [* $counter $counter 1. ] > [* $number_for_root 1.] } {break}
incr counter
}
set square_root_estimate $counter
while {1} {
set keeper $square_root_estimate
set starter $square_root_estimate
set remainder [* $starter $starter 1. ]
set remainder [- $number_for_root [* $starter $starter 1. ] ]
set square_root_estimate [+ $starter [/ $remainder [* 2. $starter ]]]
if {abs($keeper - $square_root_estimate) < $epsilon} break
}
return $square_root_estimate
}
puts " square root of 2 is >> [square_root_function 2 ] "Comments Section
Please place any comments here with your wiki MONIKER and date, Thanks. gold 12Dec2018 a.
gold 5/10/2021. Removed copyright notice on page.