Babylonian Field Expansion Procedure Algorithm and example demo eTCL calculator, numerical analysis
Babylonian Field Expansion Procedure Algorithm and eTCL demo example calculator, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 12Dec2018
- Babylonian Field Expansion Procedure Algorithm and eTCL demo example calculator, numerical analysis
- Rectangular Test Cases
- Pseudocode Section
- Appendix Code
- Console program under test.
- printout
- Crude square root of 2, to three places
- Crude Cube Root of 1000 , to three places
- Comments Section
Preface
gold Here are some TCL calculations for Babylonian Field Expansion Procedure Algorithm in calculator shell. Additional console program below is used to check or improve subroutine.
Introduction
The Babylonian field expansion procedure algorithm from clay tablets was loaded into an eTCL calculator. The Babylonians did not use algebra notation, so the reader will have to bear some anachronisms in the eTCL pseudocode. The field expansion procedure is defined as the method used by scribes to successively reduce or add numbers or number products by integer fractions, usually 1/60, 2/60, 3/60 et al. In modern notation and definitions, the numbers in base 60 that appeared on the tablet would be n+(1/60), n+(2/60), n+(3/60) until a desired goal for is reached. On some clay tablets to reach a desired field area of 100 square units called a iku (Akkadian for field), the successive altered sides a*b would be (a+(1/60))*(b+(1/60)),(a2+(1/60))*(b2+(1/60))...until (a_f+(1/60))*(n_f+(1/60)) ~= 100. Allowing for some number rounding, the field expansion procedure would produce an almost square field of 100 square units. The inherent error should be less than 1/60, error <= (/ 1. 60.). The field expansion procedure can be extended to produce rectangular fields of certain desired areas or side a/b ratios. The bare numbers on the tablets were not usually marked with units or annotated. Successive or iterated math solutions are called algorithms and the field expansion procedure is one of the earliest algorithms documented. The TCL procedures are descendants of this idea. For restating the problem in a computer algorithm, the sides and field area will be in meters and square meters, respectively.
Field Expansion Procedure
The reason for the field expansion procedure is not completely understood. However, there are some peg points or analogies available. The early examples of the field expansion procedure are from clay tablets of the proto-literate mathematical texts around 3000 BCE and metro-mathematical school texts from the Early Sumerian Dynastic III Period around 2500 BCE, ref Friberg. The successive addition and clay marks/counterpieces look somewhat like the pebble math problems, pebble games, or penny problems of some later cultures. Possibly, the concern with sides of 10 units and area of 100 square units may be a separate or earlier tradition other than base sixty. For example, one would think that side of 12 units and area of 144 square units would track better with base 60. The almost square fields or concern with squares in some problems suggest the field expansion procedure was a method that avoided square roots or predated taking square area of rectangles. Although the field expansion texts would have some utility in a scribal school setting, there is an implied interest in demonstrating that the dimensions of a particular field give an accurate area or regular area units in a land survey setting. More a conjecture, but some contend that the yield or harvest of a field would be quantity times area unit, meaning that evaluating the field in terms of standard area units would lead to better harvest supervision and better accounting to the temple management.
The multiplication term 1/60 was also found in much later cuneiform tax records as the interest rate for one (lunar) month. Possible yearly tax rate was 12*(1/60) or 12/60 for a solar year or 18*(1/60) or 18/60 for a lunar calendar. The analysis is not suggesting the field expansion procedure was calculating taxes, but it is difficult to rule out anything just looking at bare numbers without text explanation.
In the later eras, the cuneiform methods for taking areas of squares and rectangles were accurate, a*a or a*b. In those eras, the common approximate quadrilateral formula for area (a+c)*(b+d)*.25 was very inaccurate, inconsistent, and lead to unfair tax assessments. Taxes or interest were 1/60 per month or 12/60 per year of the harvest in some eras, so an accurate survey would almost pay the years taxes. There probably was some motivation to extend an accurate confirmed square area into an accurate rectangular field vis using the inconsistent approximate quadrilateral formula. The Babylonian false position algorithm on this wiki does take a square root and may be a later development.
Later reporting by Friberg indicates that equation system for a rectangle of a certain side ratio is couple of 1) linear and 2) quadratic equations. Hence the field expansion procedure in transforming a square into a rectangle with sides of fixed ratio is solving a very simple quadratic equation.
TCL Code
Depending on the settings for the correction fraction, the field expansion procedure algorithm can generate crude square roots. The accuracy of the field expansion procedure is dependent on the fineness of the intervals, which in the notation of Babylonian base 60 fractions would be 1/60/ 1/3600, or 1/216000. For square sides of 1.0001/1, desired area of 2, and correction fraction (1/60), the square root solution of 2 was 1.4, leaving off incorrect digits. For square sides of 1.0001/1, desired area of 2, and correction fraction (1/3600), the square root solution of 2 was 1.414, leaving off incorrect digits. Not sure the Babylonians and Sumerians were aware of using the field expansion procedure for obtaining square roots, but the use in the eTCL code does show the power of the field expansion procedure. At least, the Babylonians in later eras had different, faster methods, and fewer hand calculations to obtain square roots.
The first eTCL code was based on the tablet calculations and was working when solution approaches the goal from below the desired number. However, the eTCL calculator solution needs to approach correctly from either below or above the desired number goal. This routine is sort of like a double barreled Newton's method from Square Root, especially proc SqrtB. Another possible improvement for the field expansion procedure is having the slice rates or intervals proportional to the distance from the goal. In the eTCL code, distance from the goal or delta from the goal is measured by <- $goal <* $side1 $side2 1. > >. For example, if delta is less than 1/4, set the slice interval at (1/3600). If delta is greater than 1/4, set the slice interval at (1/60). Fewer computations at the higher slice rates will speed up computations and reduce wait time. Some of the Babylonian problems appeared to freeze the width of a calculated square and use a constant side a/b ratio to morph into a rectangle. Although probably not classic Field Expansion procedures, there are Babylonian math problems that increase the height of a grain bin by 1/60 or some other fraction. Meaning that modifying the Field Expansion procedure from the area a*b calculations to 3 dimensions of a*b*c or cubic equations is possible.
Conclusions
The Babylonian Field Expansion Procedure Algorithm continues to fascinate the linguists as the Field Expansion Procedure is the earliest known and documented algorithm. From the work of Friberg, Robson, and others, the Field Expansion Procedure in the cuneiform tablets of the Archaic Period actually predates the classic Sumerian URIII period by 500 years and predates the era of the Babylonian mathematicians by 1400 years. There is some evidence that the Field Expansion Procedure in the available Archaic texts predates the scribal establishment and scribal accounting of the base60 notation and even possibly the full entry of Sumerian language into Mesopotamia. For example, the area unit for iku of 100 square nindians would seem more useful to base10 calculations. Why not an iku of 60, 120, or 360 units as more useful for a base60?
Discussion on Testcases Follows
Rectangular Test Cases
Testcase 4. A rectangular field problem can be set up as follows, using modern notation. The rectangular field will have length to width ratio of 3/2 and an area of 100 square rods, rod = 6 meters. The modern notation is (1*x)*(2/3)*x=100 square rods, x*x=(3/2)*100, x=sqrt(150),x=12.24, length ~~12 rods. For the width, w=12*(2/3), 8 rods. From the easy eye calculator, the original area is <expr 12*8 > or 96 square rods. The original area is short of the goal as <expr 100-94> or 6 square rods. The eTCL calculator is loaded as 12/8/100 and the field expansion algorithm returns length/width/area as 12.19/8.2/100.039.
Testcase 5. A rectangular field problem can be set up as follows, using modern notation. The rectangular field will have length to width ratio of 3/2 and an area of 1800 square rods, rod = 6 meters. The modern notation is (1*x)*(2/3)*x=1800 square rods, x*x=(3/2)*1800, x=sqrt(2700),x=51.961, length ~~50 rods. For the width, w=50*(2/3), 33 rods. From the easy eye calculator, the original area is <expr 50*33 > or 1650 square rods. The original area is short of the goal as <expr 1800-1650> or 150 square rods. The eTCL is loaded as 50/33/1800 and the field expansion algorithm returns length/width/area as 50/33/1719. A second run on the eTCL calculator is loaded as 51/33/1800 and returns 51.83/33.83/1753 square units.
Testcase 6. A rectangular field problem can be set up as follows, using modern notation. The rectangular field will have length to width ratio of 3/2 and an area of 11700 square rods, rod = 6 meters. The modern notation is (1*x)*(2/3)*x=11700 square rods, x*x=(3/2)*11700, x=sqrt(17550),x=132.476, length ~~132 rods. For the width, w=132*(2/3), 88 rods. From the easy eye calculator, the original area is <expr 132*88 > or 11616 square rods. The original area is short of the goal as <expr 11700-11616> or 84 square rods. The eTCL calculator is loaded as 132/88/11700 and the field expansion algorithm returns length/width/area as 132.38/88.38/11700.48.
Pseudocode Section
# using pseudocode for Babylonian field expansion procedure algorithm.
# possible problem instances include add 1/60 to sides until area goal reached
long_side = supplied value
short_side = supplied value
desired_goal = supplied value
# desired_goal usually 100 square units in some early math problems
set old_field_area = a*b , old field_area = long_side * short_side
set new_side_a = long_side + 1/60
set new_side_b = short_side + 1/60
set new_field_area = (long_side + 1/60) * ( short_side + 1/60 )
is new_field_area =? desired_area within +/- (1/60) , yes = finished loop
check error , abs (desired_goal - new_field_area) <= [/ 1. 60.]
half area = area * .5
quarter area = area * .25
check_answer new area =? desired goal , desired goal reached (yes/no)
set answers and printout with resulting valuesTestcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
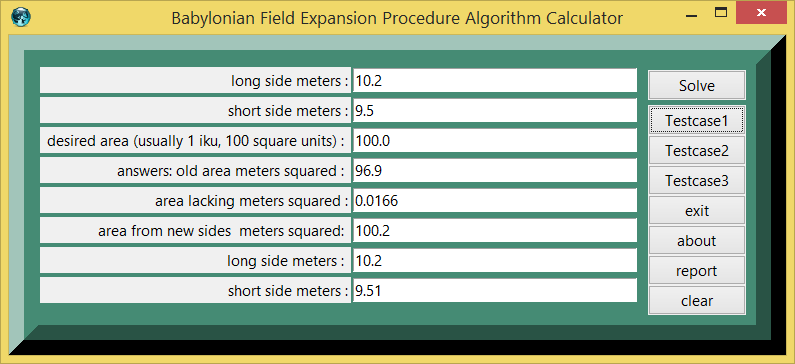
Testcase 1 , almost square field
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 10.2 : | long side meters | |
| 9.5 : | short side meters | |
| 100.0 : | desired area (usually 1 iku, 100 square units) | |
| 96.899 : | answers: old area meters squared | |
| 0.166 : | area lacking meters squared | |
| 100.211 : | area from new sides meters squared | |
| 10.366 : | long side meters | |
| 9.666 : | short side meters |
Testcase 2 , almost square field
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 9.599 : | long side meters | |
| 9.060 : | short side meters | |
| 100.0 : | desired area (usually 1 iku, 100 square units) | |
| 86.975 : | answers: old area meters squared | |
| 0.683 : | area lacking meters squared | |
| 100.193 : | area from new sides meters squared | |
| 10.283 : | long side meters | |
| 9.743 : | short side meters |
Testcase 3 , almost square field
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 9.5 : | long side meters | |
| 9.0 : | short side meters | |
| 100.0 : | desired area (usually 1 iku, 100 square units) | |
| 85.5 : | answers: old area meters squared | |
| 0.7666 : | area lacking meters squared | |
| 100.271 : | area from new sides meters squared | |
| 10.266 : | long side meters | |
| 9.766 : | short side meters |
Testcase 4 , rectangular field
| table 4 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 12.0 : | long side rods | |
| 8.0 : | short side rods | |
| 100.0 : | desired area (usually 1 iku, 100 square units) | |
| 96.0 : | answers: old area rods squared | |
| 0.200 : | area lacking rods squared | |
| 100.0399 : | area from new sides rods squared | |
| 12.199 : | long side rods | |
| 8.199 : | short side rods |
Testcase 5 , rectangular field
| table 5 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 5: | testcase_number | |
| 50.0 : | long side rods | |
| 33.0 : | short side rods | |
| 1800.0 : | desired area (usually 1 iku, 100 square units) | |
| 1650.0 : | answers: old area rods squared | |
| 0.833 : | area lacking rods squared | |
| 1719.861 : | area from new sides rods squared | |
| 50.833 : | long side rods | |
| 33.833 : | short side rods |
Testcase 6 , rectangular field
| table 6 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 6: | testcase_number | |
| 132.0 : | long side rods | |
| 88.0 : | short side rods | |
| 11700.0 : | desired area (usually 1 iku, 100 square units) | |
| 11616.0 : | answers: old area rods squared | |
| 0.383 : | area lacking rods squared | |
| 11700.480 : | area from new sides rods squared | |
| 132.383 : | long side rods | |
| 88.383 : | short side rods |
Screenshots Section
figure 1.
References:
- A Geometric Algorithm with Solutions to Quadratic Equations
- in a Sumerian Juridical Document from Ur III Umma
- Joran Friberg, Chalmers University of Technology, Gothenburg, Sweden
- Geometric division problems, quadratic equations, and recursive
- geometric algorithms in Mesopotamia,Joran Friberg
- google search engine <Trapezoid area bisection>
- Wikipedia search engine <Trapezoid area >
- mathworld.wolfram.com, Trapezoid and right trapezoid
- Mathematical Treasure: Old Babylonian Area Calculation, uses ancient method
- Frank J. Swetz , Pennsylvania State University
- Wikipedia, see temple of Edfu, area method used as late as 200 BC in Egypt.
- Oneliner's Pie in the Sky
- One Liners
- Category Algorithm
- Babylonian Number Series and eTCL demo example calculator
- Brahmagupta Area of Cyclic Quadrilateral and eTCL demo example calculator
- Gauss Approximate Number of Primes and eTCL demo example calculator
- Land surveying in ancient Mesopotamia, M. A. R. Cooper
- Sumerian Approximate Area Quadrilateral and eTCL Slot Calculator Demo Example , numerical analysis
- Thomas G. Edwards, Using the Ancient Method of False Position to Find Solutions
- Joy B. Easton, rule of double false position
- Vera Sanford, rule of false position
- www.britannica.com, topic, mathematics trapezoid
- Sumerian Equivalency Values, Ratios, and the Law of Proportions with Demo Example Calculator
- Babylonian Sexagesimal Notation for Math on Clay Tablets in Console Example
- Babylonians Tracked Jupiter With Advanced Tools: Trapezoids, Michael Greshko, news.nationalgeographic.com
- Geometry in Babylonian Astronomy, Cluster of Excellence Topology, Humboldt University of Berlin
- Mathieu Ossendrijver: „Ancient Babylonian astronomers calculated Jupiter’s position
- from the area under a time-velocity graph“, in: Science, January 29, 2016.
- Late Babylonian Field Plans in the British Museum, books.google.com/books
- Karen Rhea Nemet-Nejat
- Late Babylonian Surface Mensuration Author(s): Marvin A. Powell Source: jstor
- translation: trapezoid in two babylonian astronomical cuneiform
- texts for jupiter (act 813 & act 817) from the seleucid era , 310 BC -75 AD
- Otto Neugebauer, Astronomical Cuneiform Texts, 3 Vols.
- Lund Humphreys, London, 1955:405,430-31.
- DeSegnac, MS 3908 A RE-CONSTRUCTION, D.A.R. DeSegnac
- A draft for an essay
- DeSegnac, MENTAL COMPUTING OF THREE ARCHAIC
- MESOPOTAMIAN PUZZLES W 20044, 35, W 20044, 20 & W 20214, essay draft
- DeSegnac, HARMONY OF NUMBERS I and II, D.A.R. DeSegnac, A draft for an essay
Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# Babylonian Field Expansion Procedure Algorithm Calculator V2
# written on Windows XP on eTCL
# working under TCL version 8.6
# gold on TCL Club, 12dec2018
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} { long side meters :} }
lappend names { short side meters :}
lappend names { desired area (usually round units, 1 iku, 100 square units) : }
lappend names { answers: old area meters squared : }
lappend names { area lacking meters squared :}
lappend names { area from new sides meters squared: }
lappend names { long side meters : }
lappend names { short side meters :}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Babylonian Field Expansion Procedure Algorithm V2
from TCL,
# gold on TCL Club, 12dec2018 "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg " Babylonian Field Expansion P. Algorithm V2
from TCL ,
# self help listing
# problem, Babylonian Field Expansion P. Algorithm V2
# 3 givens follow.
1) long side meters:
2) short side meters:
3) desired area (usually round units, 1 iku, 100 square units):
# Recommended procedure is push testcase
# and fill frame,
# change first three entries etc, push solve,
# and then push report.
# Report allows copy and paste
# from console to conventional texteditor.
# For testcases, testcase number is internal
# to the calculator and will not be printed
# until the report button is pushed
# for the current result numbers.
# >>> copyright notice <<<
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK license terms.
# Editorial rights and disclaimers
# retained under the TCL/TK license terms
# and will be defended as necessary in court.
Conventional text editor formulas
or formulas grabbed from internet
screens can be pasted into green console.
# gold on TCL Club, 12Dec2018 "
tk_messageBox -title "Self_Help" -message $msg }
proc calculate { } {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set true_area [* $side1 $side2 ]
set desired_area $side3
# initialize ancient correction fraction
set correction_fraction [/ 1. 60. ]
set correction_fraction [* [/ [- $desired_area $true_area] $desired_area ] 5. ]
set counter 1
while { $counter < 50. } {
if { [* [+ $side1 [/ $counter 60. ]] [+ $side2 [/ $counter 60. ]] ] > $desired_area } {; break}
incr counter
}
set correction_fraction [/ $counter 60. ]
set side4 $true_area
set side5 $correction_fraction
set side6 [* [+ $side1 $correction_fraction ] [+ $side2 $correction_fraction ] ]
set side7 [+ $side1 $correction_fraction ]
set side8 [+ $side2 $correction_fraction ]
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number reference_factor flag
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Babylonian Field Expansion Report, screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
console show;
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |& "
puts "&| $side1 :|long side meters | |&"
puts "&| $side2 :|short side meters | |& "
puts "&| $side3 :|desired area (usually round units, 1 iku, 100 square units)| |& "
puts "&| $side4 :|answers: old area meters squared| |&"
puts "&| $side5 :|area lacking meters squared | |&"
puts "&| $side6 :|area from new sides meters squared | |&"
puts "&| $side7 :|long side meters | |&"
puts "&| $side8 :|short side meters | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 10.2 9.5 100.0 96.9 0.0166 100.2 10.2 9.51}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 9.6 9.06 100. 86.9 .68 100.2 10.2 9.74 }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 9.5 9.0 100.0 85.5 0.76 100.3 10.26 9.7 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .self_help -text self_help -command { self_help }
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Babylonian Field Expansion Procedure Algorithm Calculator V2" Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
Console program under test.
from ASK12, need help on Field Expansion subroutine
gold - 2017-01-25 On the this tcl wiki, the code in Field Expansion calculator is working when solution approachs the answer from below the desired number, but the solution needs to approach correctly from either below or above the desired number. This routine is sort of like a double barreled newton's method from Square Root, especially proc SqrtB {num} {# Newton's method}. Wrote a test console program for a field_expansion_procedure at bottom of wiki page. Can someone help or load corrected code for the console program at bottom of page. I am drawing a mental blank. Babylonian Field Expansion Procedure Algorithm and example demo eTCL calculator, numerical analysis
# written on Windows 10
# working under TCL version 8.6
# TCL WIKI , 28jan2017
# console program written on Windows 10
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
proc field_expansion_procedure_function2 { side1 side2 side3 side4 epsilon } {
set counter 1
set token1 $side1
set token2 $side2
set saver1 .00001
set saver2 .00001
set epsilon [/ 1. $side4]
while { $counter < 50. } {
if { [abs [- $side3 [* $token1 $token2 1. ] ] ] < $epsilon } {break;}
if { [- $side3 [* $token1 $token2 1. ] ] > 0 } {set correction_fraction [* 1. [/ 1. $side4] ]}
if { [- $side3 [* $token1 $token2 1. ] ] < 0 } {set correction_fraction [* -1. [/ 1. $side4] ]}
#set correction_fraction [- $side3 [* $token1 $token2 1. ] ]
set token1 [+ $token1 $correction_fraction ]
set token2 [+ $token2 $correction_fraction ]
incr counter
puts "token $token1 token $token2 product [* $token1 $token2 ] correction $correction_fraction"
} }
set side8 [ field_expansion_procedure_function2 9.5 9.4 100. 60. .15 ]printout
token 9.9666666666666899 token 9.8666666666666902 product 98.337777777778243 correction 0.016666666666666666 token 9.9833333333333574 token 9.8833333333333577 product 98.668611111111588 correction 0.016666666666666666 token 10.000000000000025 token 9.9000000000000252 product 99.000000000000497 correction 0.016666666666666666 token 10.016666666666692 token 9.9166666666666927 product 99.331944444444957 correction 0.016666666666666666 token 10.03333333333336 token 9.9333333333333602 product 99.664444444444982 correction 0.016666666666666666 token 10.050000000000027 token 9.9500000000000277 product 99.997500000000556 correction 0.016666666666666666
Crude square root of 2, to three places
token 1.4128777777777797 token 1.4127777777777797 product 1.9960823271604993 correction 0.00027777777777777778 token 1.4131555555555575 token 1.4130555555555575 product 1.9968673086419808 correction 0.00027777777777777778 token 1.4134333333333353 token 1.4133333333333353 product 1.9976524444444501 correction 0.00027777777777777778 token 1.4137111111111131 token 1.4136111111111131 product 1.998437734567907 correction 0.00027777777777777778 token 1.413988888888891 token 1.413888888888891 product 1.9992231790123516 correction 0.00027777777777777778 token 1.4142666666666688 token 1.4141666666666688 product 2.0000087777777837 correction 0.00027777777777777778
Crude Cube Root of 1000 , to three places
| Approaching a cube root using the Babylonian Field Expansion Procedure Algorithm , 7/2/2020 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Q. What is the cube root of 1000. ? | |||||||||
| Initial guess N1 of 9.63 | eval * 9.63 9.63 9.63 | 893.056347000000 | |||||||
| initial error of guess | eval - 10. 9.63 | 0.369999999999999 | |||||||
| line increment | eval / 1. 60. | 0.0166666666666666 | |||||||
| check on line N3 | eval + 9.63333333 0.01666 | 9.64999333 ~~ approximate token 9.650000 | |||||||
| product on N3 | eval * 9.6500000 9.6500000 9.6500000 | 898.632125 | |||||||
| error of N3 guess | eval - 10. 9.6500000 | 0.349999999999 | |||||||
| token1 | 9.6333333333333346 | token2 | 9.6333333333333346 | token3 | 9.6333333333333346 | product | 893.98403703703741 | correction | 0.016666666666666666 |
| token1 | 9.6500000000000021 | token2 | 9.6500000000000021 | token3 | 9.6500000000000021 | product | 898.63212500000066 | correction | 0.016666666666666666 |
| token1 | 9.6666666666666696 | token2 | 9.6666666666666696 | token3 | 9.6666666666666696 | product | 903.2962962962971 | correction | 0.016666666666666666 |
| token1 | 9.6833333333333371 | token2 | 9.6833333333333371 | token3 | 9.6833333333333371 | product | 907.97657870370483 | correction | 0.016666666666666666 |
| token1 | 9.7000000000000046 | token2 | 9.7000000000000046 | token3 | 9.7000000000000046 | product | 912.67300000000125 | correction | 0.016666666666666666 |
| token1 | 9.7166666666666721 | token2 | 9.7166666666666721 | token3 | 9.7166666666666721 | product | 917.38558796296456 | correction | 0.016666666666666666 |
| token1 | 9.7333333333333396 | token2 | 9.7333333333333396 | token3 | 9.7333333333333396 | product | 922.11437037037206 | correction | 0.016666666666666666 |
| token1 | 9.7500000000000071 | token2 | 9.7500000000000071 | token3 | 9.7500000000000071 | product | 926.85937500000205 | correction | 0.016666666666666666 |
| token1 | 9.7666666666666746 | token2 | 9.7666666666666746 | token3 | 9.7666666666666746 | product | 931.62062962963182 | correction | 0.016666666666666666 |
| token1 | 9.7833333333333421 | token2 | 9.7833333333333421 | token3 | 9.7833333333333421 | product | 936.39816203703947 | correction | 0.016666666666666666 |
| token1 | 9.8000000000000096 | token2 | 9.8000000000000096 | token3 | 9.8000000000000096 | product | 941.19200000000285 | correction | 0.016666666666666666 |
| token1 | 9.8166666666666771 | token2 | 9.8166666666666771 | token3 | 9.8166666666666771 | product | 946.00217129629937 | correction | 0.016666666666666666 |
| token1 | 9.8333333333333446 | token2 | 9.8333333333333446 | token3 | 9.8333333333333446 | product | 950.82870370370699 | correction | 0.016666666666666666 |
| token1 | 9.8500000000000121 | token2 | 9.8500000000000121 | token3 | 9.8500000000000121 | product | 955.67162500000347 | correction | 0.016666666666666666 |
| token1 | 9.8666666666666796 | token2 | 9.8666666666666796 | token3 | 9.8666666666666796 | product | 960.53096296296667 | correction | 0.016666666666666666 |
| token1 | 9.8833333333333471 | token2 | 9.8833333333333471 | token3 | 9.8833333333333471 | product | 965.40674537037432 | correction | 0.016666666666666666 |
| token1 | 9.9000000000000146 | token2 | 9.9000000000000146 | token3 | 9.9000000000000146 | product | 970.2990000000043 | correction | 0.016666666666666666 |
| token1 | 9.9166666666666821 | token2 | 9.9166666666666821 | token3 | 9.9166666666666821 | product | 975.20775462963422 | correction | 0.016666666666666666 |
| token1 | 9.9333333333333496 | token2 | 9.9333333333333496 | token3 | 9.9333333333333496 | product | 980.13303703704184 | correction | 0.016666666666666666 |
| token1 | 9.9500000000000171 | token2 | 9.9500000000000171 | token3 | 9.9500000000000171 | product | 985.07487500000502 | correction | 0.016666666666666666 |
| token1 | 9.9666666666666845 | token2 | 9.9666666666666845 | token3 | 9.9666666666666845 | product | 990.03329629630161 | correction | 0.016666666666666666 |
| token1 | 9.983333333333352 | token2 | 9.983333333333352 | token3 | 9.983333333333352 | product | 995.00832870370937 | correction | 0.016666666666666666 |
| token1 | 10.00000000000002 | token2 | 10.00000000000002 | token3 | 10.00000000000002 | product | 1000.0000000000059 | correction | 0.016666666666666666 |
# pretty print from autoindent and ased editor
# Babylonian Field Expansion Procedure Algorithm Calculator V2
# console program written on Windows 10
# working under TCL version 8.6
# TCL WIKI , 2jul2020
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
proc field_expansion_procedure_function2 { side1 side2 side3 side4 side5 epsilon } {
set counter 1
set token1 $side1
set token2 $side2
set token3 $side3
set saver1 .00001
set saver2 .00001
set saver3 .00001
set epsilon [/ 1. $side5]
while { $counter < 1000. } {
if { [abs [- $side4 [* $token1 $token2 $token3 1. ] ] ] < $epsilon } {break;}
if { [- $side4 [* $token1 $token2 $token3 1. ] ] > 0 } {set correction_fraction [* 1. [/ 1. $side5] ]}
if { [- $side4 [* $token1 $token2 $token3 1. ] ] < 0 } {set correction_fraction [* -1. [/ 1. $side5] ]}
#set correction_fraction [- $side3 [* $token1 $token2 1. ] ]
set token1 [+ $token1 $correction_fraction ]
set token2 [+ $token2 $correction_fraction ]
set token3 [+ $token3 $correction_fraction ]
incr counter
puts " &| token1 | $token1 | token2 | $token2 | token3 | $token3 | product | [* $token1 $token2 $token3 ] | correction | $correction_fraction |& "
} }
set side8 [ field_expansion_procedure_function2 9.6 9.6 9.6 1000. 60. .15 ]
# printout followsComments Section
Please place any comments here, Thanks.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |