Babylonian Quarter Square V4
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold3/29/2024
- Title: Babylonian Quarter Square V4
- Preface
- Introduction
- Formulas for Quarter Squares and Half Squares
- Possible Formula for Full Square Multiplication
- Comparison of the Algorithm(s)
- Testcase with Quarter Square Tables
- Testcases with Half Square Tables
- Many Place Reciprocals have Similarity to Modern Logarithm steps
- Notes on Multiplication Methods and Modern Logarithms
- Babylonian Reciprocal Algorithms with Successive Factorizations
- BarTa Rectangle in the Babylonian math problems
- Rules of Thumb from Babylonian Tablets
- Push Button Operation
- Conclusions
- Table 1: Babylonian Quarter Squares Tables
- Table 2: Babylonian Half Squares Tables
- Table 3: Squares Tables from Modern Binomial_Theorem
- Table 4: Babylonian Exponent Tables or Babylonian Logarithms??? Tables in base 16 and base_2
- Table 5, Math Terms Associated with Babylonian Trapezoids
- Table 6 : Babylonian regular_twins Reciprocals
- Table 7 : Powers of 2 with added Modern Logarithm Notation
- Testcases Section
- Screenshots Section
- References:
- Pseudocode & Equations Section
- Appendix Code
- Comments Section
Title: Babylonian Quarter Square V4
Preface
gold Here is some TCL scripts on the Babylonian quarter square multiplication algorithm. In reference to modern mathematics, the Babylonian multiplication algorithms and modern extensions fall under the broad umbrella of the binomial theorem and algebra . Aside from the TCL calculator shell or graphics user interface gui, separate console programs were developed to dump the quarter square tables and check the algorithms as independent TCL procedures.
Introduction
The Babylonian quarter square multiplication algorithm from clay tablets was loaded into TCL scripts. The Babylonians did not use algebra notation, so the reader will have to bear some anachronisms in the pseudocode and TCL scripts. The Babylonian quarter square multiplication algorithm is defined as the method used by Babylonian Scribes to multiply two or more numbers from a table of quarter squares, half squares, or whole squares, as a broad definition. The bare numbers in the Babylonian multiplication tables do not tell the complete method, as there are mental and undocumented components of the Babylonian multiplication methods, meaning actions, table lookup, and calculations off the clay tablet. For that matter, some modern quarter square tables and publications did not include any instructions, complete instructions, or any explanation on how the tables were generated. Zip instructions on algorithms and code are called job security in some quarters. In modern terms, the integer number pairs in Babylonian base_60 notation that appeared on the tablet may be N,int<N*N*.25>,<N+1>,int<(N+1)*(N+1)*.25>, <N+2>,int<(N+2)*(N+2)*.25>, until a desired goal is reached. In Babylon, the desired end goal was usually 60 for base_60, but the algorithm steps, notation, and desired goal can be transformed into base 10, base 16, or other bases for modern schemes and computer algorithms. In reference to modern mathematics, the Babylonian multiplication algorithms and modern extensions fall under the broad umbrella of the binomial theorem and algebra . The 2007 paper of David McFarland provided an excellent history of the quarter square multiplication algorithm in both the ancient and modern eras. The college institutes, textbooks, and computer companies in the USA that previously used the Babylonian mathematical ideas without credit may be glad to know that the Babylonian copyrights and patents expired about 4000 years ago.
In the cuneiform math problems and coefficient lists on clay tablets, there are coefficient numbers which were used in determining the amount of materials and the daily work rates of the workers. In most cases, the math problem is how the coefficient was used in estimating materials, work rates, and math problems. One difficulty is determining the effective magnitude or power of the number coefficient in the base 60 notation. In cuneiform, numbers in base 60 are written on clay tablets using a notation of relative place value. For example, 20 could represent either 20*3600,20*60,20,20/60, 20/3600, or even 1/20. The basic dimensions and final tallies were presented in the cuneiform accounts on clay tablets, but some calculations, some units, and some problem answers (aw shucks!) were left off the tablet. Successive or iterated math solutions are called algorithms and the multiplication methods are some of the earliest algorithms documented, ref the bulk of math tablets were circa 1600 BCE. The TCL procedures are descendants of this idea. The Babylonians did not use algebra notation, decimal notation, or modern units, so the reader will have to bear some anachronisms in the TCL code. At least one approach for the modern reader and using modern terminology is to develop the implied algebraic equations and decimal equivalents from the cuneiform numbers. Then the TCL calculator can be run over a number of testcases to validate the algebraic equations. For the examples of presenting algorithms to modern readers, the calculator shell will give product of long back side and short front side in meters for product of field area in meters squared. The units can be changed in the internal calculator formulas as TCL code. Any convenient and consistent output units might be used like millimeters, inches, cubits, feet, or dollars to donuts.
Formulas for Quarter Squares and Half Squares
From the tablets and including modern derivations and formula extensions, there are a number of formulas that can be presented for the Babylonian quarter square multiplication algorithm into TCL code. The quarter square multiplication formula for the tables is x*y = <.25* (x+y)**2> * <.25* (x-y)**2>. As an extension, the half square multiplication formula for the tables may be equivalent to x*y = 0.5* <.5* (x+y)**2> * <.5* (x-y)**2>. But there is some uncertainty specific to how the Babylonian half square tables were used, as the tablet CBS-1535 includes integers and half fractions < N, (N+.5), (N+1), (N+1+.5) ...> in base_60 notation. Also rearranging terms from the quarter square formulation, x*y = .25*{ <(x+y)**2> * < (x-y)**2>}. The above rearranged formula x*y = .25*{ <(x+y)**2> * < (x-y)**2>} could be interpreted as an extension for a whole square formula. However, one can not jump too far on the whole square formula, as evidence of Babylonian usage would have to carefully documented, if any usage at all. The modern extension to the multiplication algorithm from the binomial theorem is a*b = 0.5*{a+b)**2 -a**2-b**2}. ---
The conventional Western formula for quarter square multiplication tables is a*b= expr (1/4)*(((a+b)**2) - ( (a-b)**2 ) ). A second Western formula is a*b = <(a + b)**2 − a**2 − b**2> * .5, need to check. Another Western formula with variable changes and rearranged in modern publication variants is a*b = expr <(a + b)**2 − (a − b)**2> * .25 . In opinion for the TCL procedures, the division operation of terms by 2 and 4 should be avoided and replaced by multiplication by .5 and .25 respectively, because of possible computer division by zero. Also for the TCL procedures, and although some original ancient formulas and modern extensions used positive integers only, the TCL equivalent formulas are written in the code as floating point typed variables , where possible. The modern reference tables used positive numbers including the extant Babylonian tablets, so the validity of negative terms and mixed positive/negative (+,-) numbers in products would have to be checked in possible methods using the tables etc. Not a mathematical proof, but the multiplication algorithm in the initial TCL calculator shell seems working correctly with negative and mixed (+/-) numbers.
Possible Formula for Full Square Multiplication
Maybe some redundant material here on (1/4) equaling 0.25, but the Babylonians with their math tables could look up reciprocals and squares. The above rearranged formula a*b = a*b = expr <(a + b)**2 − (a − b)**2> * .25 could be interpreted as an extension for a full squares multiplication algorithm. Such that the hypothetical Babylonian method or procedure for a full squares algorithm may boil down and finish out to multiplication of 3 terms as ( square1 - square2 )* reciprocal. As the mathematician papers and others have suggested, the version a*b = expr <(a + b)*2 − (a − b)*2> * .25 would probably be the easiest for the Babylonians. Reference. Google Babylonian Multiplication by M. Lewinter and W. Widulski.
Comparison of the Algorithm(s)
For comparison of the Babylonian algorithm(s) with conventional Western methods, TCL code may include redundant procedures, redundant calculation paths, and printout check formulas to compute product, area, check diagnostics, and relative errors. The Babylonian quarter square multiplication algorithm is believed to be derived from the Sumerian Scribal land survey practices of averaging two opposite sides of a field to calculate the diagonals or area of a field. These averages of opposite sides were used in the approximate quadrilateral formula expr <((a+c)/2) *((b+d)/2) >, where the four contiguous sides of the field are a,b,c,&d. At least the Sumerians were averaging field sides (a+c)/2 circa 3000 BCE. As seen in the quarter square and half square formulas, sum and difference methods in general were an interesting staple of land surveyor's riddles, ref Friberg. But the extant Babylonian algorithms and tables discussed here are probably from a later period circa 1600 BCE.
Testcase with Quarter Square Tables
For trials of the quarter square table, try multiplying 7 by 4. Some formulas can be pasted into the TCL console. The sum is expr {7+4}, 11. The difference is expr {7-4}, 3. From lookup 1 on the quarter square table, the quarter square or counterpart of 11 is 30. Likewise from lookup 2, the quarter square or counterpart of 3 is 2. The result from quarter square method is expr {30-2} or 28. The check answer from the TCL console is expr { 7*4}, 28. The overhead work is 2 lookups and 3 operations, which are abbreviated <ops,1+,2-,2L,3->.
Testcases with Half Square Tables
For the trial method for the half square table, a testcase of 7*4 was entered and a second testcase of 7.5*4.5 was entered. For testcase 1 of the half square table, try multiplying 7 by 4. The sum is expr {7+4}, 11. The difference is expr {7-4}, 3. From lookup 1 on the half square table, the half square or counterpart of sum 11 is 60. From lookup 2 on the half square table, the half square or counterpart of difference 3 is 4. The trial product from the half square method is expr {(60.-4.)*.5} or 28. even. The check answer from the TCL console is expr { 7*4 }, 28. The overhead work is 2 lookups and 4 operations, which are abbreviated <ops,1-,2+,2L,3-,4*>. For the second trial or testcase of the half square table, try multiplying 7.5 by 4.5. The sum is expr {7.5+4.5}, 12. The difference is expr {7.5-4.5}, 3. From lookup 1 on the half square table, the half square or counterpart of sum 12 is 72. From lookup 2 on the half square table, the half square or counterpart of difference 3 is 4. The trial product from the half square method is expr {(72.-4.)*.5} or 34? The check answer from the TCL console is expr { 7.5*4.5 }, 33.75. The overhead work is 2 lookups and 4 operations, which are abbreviated <ops,1-,2+,2L,3-,4*>. Commenting on the fourth possible operation, the Babylonians tended to use the reciprocal 1/N or multiply ½ for division, as recommended above for the TCL procedures.
Note that the quarter squares function QS() entries above were QS(7) and QS(4) giving 28 in the method, which are the very same number entries as used in the half squares function HS(). But QS(7) and QS(4) are not the same numbers as HS(7) and HS(4). Except for the initial and trivial entries of 0 through 1, generally the quarter square function QS() does not equal half squares function HS(). As a gist for the above examples, evaled functions QS(7+4) - QS(7-4) = 28 and evaled functions HS(7+4) - HS(7-4) = 28.
Many Place Reciprocals have Similarity to Modern Logarithm steps
The Babylonian Market Rate Algorithm is taking 1) base_60 reciprocals of several numbers, 2) summing the reciprocals, and 3) using the sum as a multiplication factor. The Market Rate Algorithm has initial steps and similarity to multiplication of several terms using modern logarithms. For example, take the base_60 logarithms of several numbers { 50 40 30 }, resulting in the set { 6/5 6/4 2 }, summing the base_60 reciprocals for a factor expr { 6./5+6./4+2. }, which equals 4.7 decimal. The return reciprocal or anti-reciprocal in base_60 is expr { 60/4.7 } is 12.76 decimal and with a factor approximating average is expr { 3.*60/4.7 } is 38.29787. The average of the original three numbers is expr { (50+40+30.)/3. } or decimal 40.0 For a modern example using natural logarithms, take the problem 50*40*30 = 60000. Take the sum of natural logs as expr { log(50)+log(40)+log(30) } = 11.0020998 decimal. The answer is the antilog expr { 2.718281828**11.0020998 } = 60000. Note: The reciprocal formulas in base_60 are N*R=60, N=60/R, and R=60/N.
In the Late Babylonian period, there were numerous tablets and fragments showing many place reciprocals and factoring other numbers in base_60. The many place reciprocals are reciprocals with 5 to 10 places in base_60. The most unusual tables were many place reciprocals between 1 and 2, ref Friberg and Al-Rawi. Although less common or less extant, there are tables of many place reciprocals between 2 and 4. The square root of sixty is decimal 7.74, so continuing the tables beyond integer 8 would be redundant and not be useful. The tablets with many place reciprocals between 1 and 2 are generated for numbers between 60 and 30. The tablets with many place reciprocals between 2 and 4 are generated for numbers between 30 and 15. Because the Babylonians used relative place notation like a modern slide rule, remember that the calculated many place reciprocals between 60 and 15 could been used in relative base_60 places like 20,20*60,20*3600,20*216000 , and so on.
In addition, there are rare LB. fragments or tables that have numbers in reciprocal pairs in base_60 with the added glyph ibsi, which means either square or square root, ref Friberg and Al-Rawi. In a general sense on other tablets, the term ibsi is associated with square roots, cube roots, raising a number in exponent, or the reverse, but the term ibsi linked with reciprocals is curious. The minimal conclusion is that the Late Babylonian mathematicians considered the regular base_60 reciprocals involved with squares, square roots, or powers. A complete explanation of the many place reciprocal tables is not available, but it has been proven that the many place reciprocals and square tables were used in school copying exercises, school multiplication assignments, and factoring algorithms. There are two multiplication formulas from the Old Babylonian tablets that used differences, sums, and squares. With a squint eye of the amateur, the Old Babylonian tables with many place reciprocals in base_60 look somewhat like the many place numbers (meaning digits) in the modern tables for decimal and natural logarithms.
In New Mathematical Cuneiform Texts, Friberg and Al-Rawi discussed a new method of algorithm for generating regular reciprocals in base_60. The tablet SM-2685 is an Atypical Ur III Table of reciprocals, that include additional and different reciprocal pairs from the later Standard reciprocal tables and two different method(s) than the Old Babylonian standard table of reciprocals (later era circa 1600 -1800 BCE.) The first method is “reciprocal compensation” and is related to the Old Babylonian doubling and halving algorithm. The second method is called “regular twins”. While the detailed discussion, base_60 features, and terms of Friberg and Al-Rawi are in the narrow corridor of math historians and linguists, the broad principles can loaded into TCL expressions using modern algebra and base_10.
Another later tablet CBS-29-31-21 has garbled text and procedures, but some cuneiform mathematical terminology may have an explanation now from the recent work of Friberg and Al-Rawi. The a-ra-kara (Sumerian) or arakum (Akkadian) procedure is to multiply a base_60 reciprocal by a high power of 2 and take reciprocal. The arakum math operator or procedure is apparently the cuneiform name or equivalent of the reciprocal compensation procedure. The reciprocal compensation method takes a known or standard reciprocal pair, N1*R(N1)=60. Then the terms of the old reciprocal pair are transformed into a new reciprocal pair as N1*2**A and R(N1)*(1/(2**A)). The check on the new pair would be the evaled new pair, { N1*2**A}* {R(N1)*(1/(2**A))}=60. The raising by powers of 2 assures that the new reciprocal pair is compatible with the defined regular pairs under number 60 on the numberline. However, since all the Old Babylonian standard table of regular numbers are defined as the product of (2**A)*(3**B)*(5**C), additional new reciprocal pairs could be defined by multiplication N1 by factors (2**A), (3**B), (5**C), or even (2**A)*(3**B)*(5**C). Of course, the other pair would use the factors of 1/(2**A), 1/(3**B), 1/(5**C), or even 1/((2**A)*(3**B)*(5**C)). While all the textual evidence and detail in not justified, the exciting part is evidence of new exponent considerations for 2,3, and 5 proceding from the set of Standard base_60 regular numbers.
Notes on Multiplication Methods and Modern Logarithms
As the first term in the Taylor series, the natural log N1 approximates expr (N1-1.) - .5*(N1-1)*(N1-1), for very small N1, best when N1 < 1.25. The natural log of 2 is expr log(2) = 0.6931 decimal. The approximate natural log of 2 equals expr (2.-1.) - .5*(2.-1)*(2.-1), 0.5 decimal. Returning to the problem of 50*40*30 using modern base_60 logarithms, the sum of logs is expr { 0.95546+0.90096+0.830706} , 2.687126. The antilog in base_60 is expr 60**2.687126= 59995.193. Kind of hokey math, but the base_60 logarithms are not that far off scale from the natural logarithms, about 8 percent off in scale. expr 2.92-2.92*.08=2.6864, expr 60**2.6864= 59817.122.
The challenge would be to find out if the Babylonian mathematicians used many place reciprocals, many place squares, or factors with the two known Babylonian multiplication formulas. It would not be surprising if some odd notations or glyphs are associated with possible use of the multiplication formulas, especially with the Late Babylonian Astronomers. For example, there was a unique “three wedge” glyph (<<<) for multiplication in some Late Babylonian multiplication tables. The “three wedge” glyph for multiplication may be a sort of brand name or associated quality signature for the modern student or readers. Maybe coincidence, but the Late Babylonian symbol for the “Astronomy zero” was either space, one wedge (<), two wedges (<<) or three wedges (<<<) . The space between base_60 places was probably separator intent and a single wedge was probably also separator intent between base_60 places. The single wedge between base_60 places looks like Babylonian ten glyph, ref Greek jot and Latin inscriptions. Also, a rare variant glyph for nine (9 decimal) was the “three wedge” glyph (<<<). While the “Astronomy zero” is very rare on the Late Babylonian clay tablets, the understanding here is that “Astronomy zero” is indicative of extreme care in error free calculations by the Late Babylonian Astronomers. In opinion, the extreme care in Late Babylonian calculations would track with the advanced and remarkable many place reciprocals or squares. In the Astronomy calculations with accumulative variables, one early mistake in the sequence would throw the whole table of accumulated variables for the lunar and planet settings. Another reference is tablet W23281, which has many place reciprocals at regular intervals, N1, N1+1, N1+2. The tablet W23281 does not have logarithms, but like the modern logarithms evaluated at regular intervals, regular intervals are needed for useful logarithm work. However, there are a few cases where the Babylonian mathematicians interpolated between two base exponents for an answer, but detailed Babylonian knowledge of logarithms has not been assessed by the professionals. In opinion, the many place reciprocals or factors were associated with the “Astronomy Group” of the Late Babylonian mathematicians. But almost all professional and cuneiform linguists have cited a lack of evidence on the association of many place reciprocals or factors with the “Astronomy Group”.
In New Mathematical Cuneiform Texts, Friberg and Al-Rawi discussed a new method or algorithm for generating regular reciprocals in base_60. The tablet SM-2685 is an Atypical Ur III Table of reciprocals, that includes additional and different reciprocal pairs and two different method(s) than the Old Babylonian standard table of reciprocals (later era circa 1600 -1800 BCE.) The first method is “reciprocal compensation” and is related to the Old Babylonian doubling and halving algorithm. The second method is called “regular twins”. The tablet SM-2685 limits itself to reciprocal pairs under the condition N1*R(N1) = 60 even, meaning the numbers in the listed reciprocal pairs are under 60. But tablet SM-2685 includes reciprocal pairs as separate integers, fractions, and mixed integers plus fractions. While the detailed discussion, base_60 features, and terms of Friberg and Al-Rawi are in the narrow corridor of math historians and linguists, the broad principles of reciprocal compensation and Babylonian regular twins can loaded into TCL expressions using modern algebra and converted to decimal notation.
Another later tablet CBS-29-31-21 has a reciprocal table with partially readable sections from early OB. Nippur and some terminology that may used for a reciprocal compensation algorithm with numbers beyond 60. While the dating and era of CBS-29-31-21 is uncertain, some of the reciprocal numbers do qualify the tablet as a many place reciprocal tablet. The concern of the tablet CBS-29-31-21 is developing many place reciprocal pairs compatible with the Old Babylonian standard table of reciprocals, or rather the set of reciprocals used in its contemporary era. Compatible pairs would have the original condition of N1*R(N1) = 60 and generally factorable by 2,3, or 5. The tablet CBS-29-31-21 is using reciprocal compensation and developing reciprocal pairs with a factors that are high powers of 2. In other words, the tablet CBS-29-31-21 is not restricting the reciprocal pairs to 60 and below, like the much earlier tablet SM-2685.
On the Babylonian clay tablet and proposed scheme for generating a new reciprocal table, the reciprocal compensation algorithm was applied to the set of powers of 2 from 2**1 to 2**14, ref Friberg and Al-Rawi. In modern notation, modern terminology, and considerable added assumptions, the initial line and derivation scheme for {2, 4, 15 } has effectively 3 propositions that 1) log2 4 = 2.0, 2) the base_60 reciprocal is 15, and 3) the known reciprocal pair is {4, 15 }. The check answer is that expr {(4*15)} = 60. While logarithms are not terms that the Babylonian mathematicians used, the reciprocal compensation algorithm was applied to the known reciprocal pair {4, 15 } to produce the compensated reciprocal pair { (4/3), 45 }. In the results with modern logarithm rules and many assumptions, the compensation changed reciprocal pair has effectively 3 propositions that 1) log2 4 - (log2 3?) =? 2.0 – 1.584962? , 2) the base_60 reciprocal = 45, and 3) the compensation changed reciprocal pair is {(4/3), 45 }. Numbers with question marks were not on tablet. The check answer is that expr {(4/3)*45} = 60. From this clay tablet and numerous other tablets, the Babylonian mathematicians seem concerned with producing new reciprocal pairs from table of powers, or tables of special reciprocal pairs for reciprocal factoring algorithms.
Is there some built-in relationship between reciprocals and modern logarithms that would imply some knowledge of the Babylonian mathematicians about logarithms? The Babylonian reciprocal compensation algorithm produced new reciprocal pairs and new reciprocal pairs intervals, but apparently did not produce new logarithm intervals. However, the base_60 in the Babylonian tables is different enough from base_10 that any possible log relationships do not automatically pop out to eye. There are tables of powers based on numbers 2,9,16,100, and 225, which were apparently used either on reciprocal algorithm(s) factoring a reciprocal or generating tables of reciprocals, including the Late Babylonian many place reciprocal tables.
To make a chicken, it is said that God starts with nothing and makes a chicken, 0 --> 1. To make a chicken, man starts with two chickens and the two chickens make a chicken, 2 --> 3. Some of the reciprocals are derived from a known standard reciprocal pair and then use the reciprocal compensation with compensation factors (2,1/2), (3,1/3), or (5,1/5). The original reciprocal pair has the defining condition N2 * R(N2) = 60, multiply N2 by F1 and R(N2) by {1/F1}, where F1 is factor 1. Not sure this concept is universal to all bases, but the Babylonian reciprocal compensation factors (2,1/2), (3,1/3), or (5,1/5) follow the decimal base_10 rule that a reciprocal of F4 is 1/F4, meaning F4*R(F4) = 1. Apparently, Babylonians were aware and used both definitions N1*R(N1) = 60 and F4*R(F4) = 1 in their mathematics. Under Babylonian reciprocal compensation, the new reciprocals retain the defining regular condition and consider that { N2*F1} * { R(N2)*(1/F1) } = 60. As a concept, the inverse of reciprocal compensation is possible either as a single operation or else as a repetitive algorithm in factorization steps. If the student can identify or factor C1 in the terms in a reciprocal pair, the student can pull or factor out the C1 term to reduce the reciprocal pair to a smaller pair, hopefully listed in the standard reciprocal table. As demonstrated in much later Babylonian tablets, the combined factors of a many place number or reciprocal pair can be factored out like { N2*(F1*F2*F3) } * { R(N2)*(1/(F1*F2*F3)) } = 60. The reciprocal pair with combined factors can be reduced to N1*R(N1) = 60, using algorithm steps, TCL do-loop steps, or line on clay tablet for each individual factor.
Successive or repetitive operations with reciprocal compensation was also used for an algorithm. In extensions and using modern algebraic notation, the reciprocal compensation algorithm effectively brings powers of 2,3,5, or combined products of the same powers into play for writing tables of reciprocals. Not sure that the Babylonians used some or all factor combinations of powers 2,3,5, but modern algebra indicates a possible extension of reciprocal compensation formula as combined compensation factors {(2**A)*(3**B)*(5**C)}, {1/(2**A)*(3**B)*(5**C) }. With the modern algebra notation, the possible factor {(2**A)*(3**0)*(5**0)} would reduce to {(2**A)*1*1}. Another extension might be to add constant Kay factor or rate factor Kay/N3, but a casual reading indicates the Babylonians did not use this extension, especially since the factors 2,3,&5 must be maintained for Babylonian reciprocals in general. A TCL procedure or do-loop that takes a known reciprocal pair and ramps through some range of reciprocal compensation factors in base10 should be fairly easy.
start with 2 * 30 = 60, as standard reciprocal reciprocal pairs
compensation factors are {(2/3),(3/2)}
2*(2/3)=4/3
30*(3/2)=90/2
check, (4/3) * (90/2) = 60
another check, (2/3)*(3/2) = 1.0start with 2 * 30 = 60, as standard reciprocal pairs expr (2.*(2**10)) = 2048 decimal integer & base_10 expr (30.*(1./2**10)) = 0.029296875 decimal fraction & base_10 check, expr (2048*0.029296875) = 60.0 another check, (2**10)(1./2**10) = 1.0
Babylonian Reciprocal Algorithms with Successive Factorizations
As a concept, the inverse of reciprocal compensation is possible either as a single operation or else as a repetitive algorithm in factorization steps. About fifteen to thirty (30) factorizations or algorithm steps were roughly the practical upper limit of the reciprocal factorization problems, based on the available Babylonian problems and the size and length dimension of the clay tablets. The larger mathematical tablets were limited to about 30 lines per tablet face, although exceptions and double page are possible. On the math tablets, a single line could include from one to four numbers in base_60 notation and/or cuneiform language. But usually, there was only one operation per line, whether N1+N2, N1-N3, N1*N4, or N1*N2*N3. As a casual study, combined multiple operations on a single line like 2*2,3*3*5, or 2**5 have not been reported, ref Proust. Thus the modern combined operations or implied multiple operations in the notation have not been present on a single tablet line. The hand held tablets were small and many tablets did not have space for multiple operations on a single line, but there seems to be Babylonian stricture or mental block forbidding multiple operations on a single tablet line. Maybe, its as simple as one could look up a single line operation on the available Babylonian math tables (N1*N4 or N1*N1), but one could not easily look up multiple operations on the available tablets (meaning, N1*N2*N3).
Lets assume the Babylonian mathematician wanted to use either 2**N or a table of 2**n in a math problem for the four operations (+,-,*,/). In the Babylonian base_60 math system, reciprocals were used in place of division and the tables of reciprocal pairs were developed for a comprehensive system, at least for 0 to 60 in the schools. Hence finding 2**N without the matching inverse pair 1/(2**N) to replace division would not be useful to the either to the student or the Babylonian mathematician. Hence, one early method as reciprocal compensation algorithm was applied to the known reciprocal pair. Suppose a target number T1 could be factored as {(2**N1)*(2**N2)*(2**N3)*(2**N4)} , then its reciprocal would be {(1/(2**N1))*(1/(2**N2))*(1/(2**N3))*(1/(2**N4))}. An alternate check method or “proof” that the reciprocal was correct would be a sequence dividing the target number T1 and descending results as T1 divided by {(2**N1),(2**N2),(2**N3),(2**N4)} in succession. If T1 is evenly divided by the factors, then the result should be unity. Remember that the Babylonian reciprocals were used in place of division, so using modern notation, the Babylonian equivalent method or check would be T1 multiplied by {(1/(2**N1)),(1/(2**N2)),(1/(2**N3)),(1/(2**N4))} in succession. Since the regular numbers were the product of powers { 2,3,5}, the Babylonian equivalent method or check for T1 composed of those factors would be T1 multiplied by {1/(2**A)),(1/(3**B)),(1/(5**C)) } in succession. Other divisor sequences for composite factored numbers might be {1/(2**A1)),1/(2**A2)),(1/(3**B1)), (1/(3**B2))} or {1/(2**A1)),1/(2**A2)),(1/(3**B)),(1/(5**C1)),(1/(5**C2)) }, and other repetitive sequences.
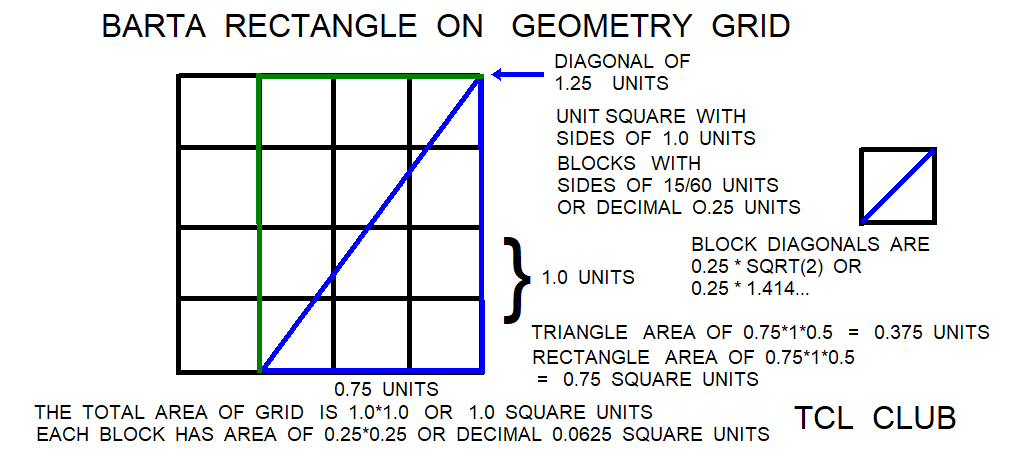
BarTa Rectangle in the Babylonian math problems
One of the favorite rectangles in the Babylonian math problems was the Bar-Ta rectangle. The Bar-Ta rectangle is related to the 3/4/5 triangle scaled by 1/4. Meaning divide the dimensions of the 3/4/5 triangle by 4 to get 3/4 4/4 5/4>. The Bar-Ta rectangle is two of the rescaled triangles. The tablet asks for the sides of a rectangle whose area is 0:45 and whose diagonal is 1:15 in base_60. Converting to base_10, the equivalent decimal numbers are 0.75 for the area, and 1.25 for the diagonal. Then in decimal, Side a = 1 , then side b= 0.75. a*b=0.75 decimal.
Rules of Thumb from Babylonian Tablets
Here are some rules of thumb from Babylonian brick constants and Babylonian math problems. A sun dried brick has water content and also as hidden water. Some sun dried bricks have straw content. Straw content should not be a factor in fired bricks. Sun dried brick weight over wet and heavy brick weight equals 40/60 or second try equals 48/60. Sun dried brick weight over baked brick weight equals 50/60. Fraction 1/6 is mortar for clay wall. Weights of wet and sun dried bricks in table BM36776 have factors 3/2 and 6/5, per Friberg and Robson. Second and third section of factor equals 3/2. Fourth section has factor equals 6/5. Water approximates 12/60 weight of wet brick. Weight loss (water) is 10/60 of dried brick to baked brick. { 1 kus ba.an.gi4 } means 1 cubit returned or 1 cubit back, used in brickwork. The daily cartage quota is 37_30 talents per us per day equals expr {(37+30./60.)*30.} or 1125 kg per 60*6 meters per day. The daily cartage quota is 1_15 talent per danna per day equals expr {(1.+15./60.)*30} or 37.5 kg per 10.8 kilometers per day.
Push Button Operation
For the push buttons, the recommended procedure is push a testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console. For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2)., TC(3), TC(4) etc. The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. For comparison of the Babylonian algorithm with conventional Western methods, TCL code will include redundant procs, redundant calculation paths, and printout check formulas to compute product and area.
Conclusions
By inspection of the quarter squares table, one can see that many of the calculated quarter squares in the table are in fact, the square of some other number. For example in the table, 10 has the quarter square QS(10) or counterpart of 25. Yet QS(10) or 25 is the square of 5. The number N in the first column of the quarter squares table can be a prime number and integer, but generally the values of quarter squares QS(N) are not primes, in the short table version. But one can find some sneaky primes just under the surface of the quarter squares table in primes that are QS(N)-1 or even N2**2-1. If QS(a) and QS(b) do not solve the problem of easy hand multiplication of the product a*b, then the set of N and QS(N) over the numberline do bring a harvest of very interesting numbers.
The Old Babylonian quarter squares multiplication formula requires three math operations as opposed to one math operation in modern logarithms, per two numbers. Considering hand calculations and omitting the table lookups, the Old Babylonian quarter squares multiplication formula is about three times the work of the modern logarithm method. Under the same considerations, the Old Babylonian half squares multiplication formula requires four math operations and is about four times the work of the the modern logarithm method. In using the Babylonian multiplication formula in taking base_60 squares, using many place numbers in a hand multiplication array, there must be breakpoints where the effort of the multiplication formula is less than taking the many place square by hand calculation. Given the amount of Babylonian effort that developed the many place reciprocals in base_60 on the clay tablets, is it possible that the known Babylonian multiplication formulas, base_60 reciprocals, and terms could be manipulated into an algorithm, formula, or even modern logarithm of fewer operations?
Table 1: Babylonian Quarter Squares Tables
| Table 1: Babylonian Quarter Squares Tables | printed in | tcl format |
|---|---|---|
| N | int <N*N*.25> | comments if any |
| 0 | 0.00000 | modern notation includes zero's |
| 1 | 0.00000 | some fractions clipped by int |
| 2 | 1.0000 | modern decimal notation |
| 3 | 2.0000 | |
| 4 | 4.0000 | |
| 5 | 6.0000 | |
| 6 | 9.0000 | |
| 7 | 12.000 | |
| 8 | 16.000 | |
| 9 | 20.000 | |
| 10 | 25.000 | |
| 11 | 30.000 | |
| 12 | 36.000 | |
| 13 | 42.000 | |
| 14 | 49.000 | |
| 15 | 56.000 | |
| 16 | 64.000 | |
| 17 | 72.000 | |
| 18 | 81.000 |
Table 2: Babylonian Half Squares Tables
| Table 2: Babylonian Half Squares Tables | printed in | tcl format |
|---|---|---|
| N | int <N*N*.5> | comments if any |
| 0 | 0.00000 | modern notation includes zero's |
| 0.5 | 0.00000 | some fractions clipped by int |
| 1 | 0.00000 | modern decimal notation |
| 1.5 | 1.0000 | |
| 2 | 2.0000 | |
| 2.5 | 3.0000 | |
| 3 | 4.0000 | |
| 3.5 | 6.0000 | |
| 4 | 8.0000 | |
| 4.5 | 10.000 | |
| 5 | 12.000 | |
| 5.5 | 15.000 | |
| 6 | 18.000 | |
| 6.5 | 21.000 | |
| 7 | 24.000 | |
| 7.5 | 28.000 | |
| 8 | 32.000 | |
| 8.5 | 36.000 | |
| 9 | 40.000 | |
| 9.5 | 45.000 | |
| 10 | 50.000 | |
| 10.5 | 55.000 | |
| 11 | 60.000 | |
| 11.5 | 66.000 | |
| 12 | 72.000 | |
| 12.5 | 78.000 | |
| 13 | 84.000 | |
| 13.5 | 91.000 | |
| 14 | 98.000 | |
| 14.5 | 105.00 | |
| 15 | 112.00 | |
| 15.5 | 120.00 | |
| 16 | 128.00 | |
| 16.5 | 136.00 | |
| 17 | 144.00 | |
| 17.5 | 153.00 | |
| 18 | 162.00 | |
| 18.5 | 171.00 | |
| 19 | 180.00 | |
| 19.5 | 190.00 | |
| 20 | 200.00 | |
| 20.5 | 210.00 |
Table 3: Squares Tables from Modern Binomial_Theorem
| Table 3: Binomial_Theorem Squares Tables | printed in | tcl format |
|---|---|---|
| a | a*a from subbing a*b = 0.5*(a+b)**2 -a**2-b**2) | comments if any |
| 0 | 0.00000 | modern notation includes zero's |
| 1 | 1.0000 | modern decimal notation |
| 2 | 4.0000 | modern notation includes zero's |
| 3 | 9.0000 | |
| 4 | 16.000 | |
| 5 | 25.000 | |
| 6 | 36.000 | |
| 7 | 49.000 | |
| 8 | 64.000 | |
| 9 | 81.000 | |
| 10 | 100.00 |
Table 4: Babylonian Exponent Tables or Babylonian Logarithms??? Tables in base 16 and base_2
| Table 4: | Babylonian Exponent tables or Babylonian logarithms Tables??? in base 16 and base_2 | printed in | tcl format |
|---|---|---|---|
| line no. | Column uses Base_60 & transliteration | Base_10 conversion & conventional modern notation | comments if any |
| >>> base_16 from MCT, MLC2078 <<< | |||
| 1 | 15_e 2 ib-si8 | 15/60 = log_16( 2 ) | MCT, MLC2078 |
| 2 | 30_e 4 ib-si8 | 30/60 = log_16( 4 ) | ib-si8 is an older & special glyph useage |
| 3 | 45_e 8 ib-si8 | 45/60 = log_16( 8 ) | 2**4 =16, tables are related |
| 4 | 1_e 16 ib-si8 | 60/60 = log_16( 16 ) | |
| 5 | 1_15_e 32 ib-si8 | 75/60 = log_16( 32 ) | |
| 6 | 1_30_e 1_4 ib-si8 | 90/60 = log_16( 64 ) | |
| >>> base_2 from MCT, MLC2078 <<< | |||
| 1 | 2_e 2 ib-si8 | 1 = log_2( 2 ) | MCT, MLC2078 |
| 2 | 4_e 4 ib-si8 | 2 = log_2( 4) | base_2 used in interest rate problems |
| 3 | 8_e 3 ib-si8 | 3 = log_2( 8) | ib-si8 is an older and special glyph useage |
| 4 | 16_e 4 ib-si8 | 4 = log_2( 16) | 2**4 =16, tables are related |
| 5 | 32_e 5 ib-si8 | 5 = log_2( 32) | |
| 6 | 1_4-e 6 ib-si8 | 6 = log_2( 64) |
Table 5, Math Terms Associated with Babylonian Trapezoids
| Table 5 , Math Terms Associated with Babylonian Trapezoids | printed in tcl format | modern equivalent, English | comment if any |
|---|---|---|---|
| sag ki.gu : | side earth | trapezoid | |
| sag ki.ta : | side earth its , possessive case | upper front of the trapezoid | |
| sag an.na : | side upper | upper front of the trapezoid | |
| us gi.na : | length front | true length of the trapezoid | |
| sag gi.na : | side front | true front of trapezoid | |
| N1 kus i-ku-lu : | N1 cubit in eats it (it or man), read left to right | feed parameter of the trapezoid | noun derived from Sumerian SOV phrase |
| sag du : | side | triangle | |
| N1 arakarum : | N1 multiply | transformation coefficient, usually scale up |
Note. These Math Terms cover 4 or 5 cuneiform languages, and 5000 years of history. Math Terms are best understanding of context and math connotation here,not blessed by linguists and cuneiform dictionaries, ref Friberg
Table 6 : Babylonian regular_twins Reciprocals
| Table 6: Babylonian regular_twins Reciprocals | printed in | tcl format | |
|---|---|---|---|
| a | a, R(a) from subbing N4, N4-1 | Check answer | comments if any |
| 40.0 | 1.5 | expr 40*1.5 = 60 | |
| 45.0 | 1.33 | expr 45*1.333 =~ 60 | |
| 48.0 | 1.25 | expr 48*1.25 = 60 | |
| 50.0 | 1.2 | expr 50*1.2 = 60 | |
| Note: These are the “pretty regular twins” Reciprocals | under 60 for base_60 | ref Friberg and Al-Rawi |
Table 7 : Powers of 2 with added Modern Logarithm Notation
| Table 7: Powers of 2 | printed in | tcl format | ||
|---|---|---|---|---|
| N | 2**N | modern notation log2 N = | base_60 reciprocal, decimals | comments if any |
| 0 | 1.0000 | log2 1 = 0.0 | 60.000 | |
| 1 | 2.0000 | log2 2 = 1.0 | 30.000 | |
| 2 | 4.0000 | log2 4 = 2.0 | 15.000 | Ref MCT |
| 3 | 8.0000 | log2 8 = 3.0 | 7.5000 | |
| 4 | 16.000 | log2 16 = 4.0 | 3.7500 | |
| 5 | 32.000 | log2 32 = 5.0 | 1.8750 | |
| 6 | 64.000 | log2 64 = 6.0 | 0.93800 | |
| 7 | 128.00 | log2 128 = 7.0 | 0.46900 | |
| 8 | 256.00 | log2 256 = 8.0 | 0.23400 | |
| 9 | 512.00 | log2 512 = 9.0 | 0.11700 | |
| 10 | 1024.0 | log2 1024 = 10.0 | 0.059000 |
Testcases Section
Testcase 1
| table 1 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 11.0 : | long side meters | |
| 10.0 : | short front side meters | |
| 1.0 : | optional meters | |
| 1.100 : | answers: ratio long over short | |
| 110.25 : | squared term1 | |
| 0.25 : | squared term2 | |
| 110.0 : | check product (expr a*b) square meters | |
| 110.0 : | product from algorithm square meters |
Testcase 2
| table 2 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 61.0 : | long side meters | |
| 60.0 : | short front side meters | |
| 1.0 : | optional meters | |
| 1.0166 : | answers: ratio long over short | |
| 3660.25 : | squared term1 | |
| 0.25 : | squared term2 | |
| 3660.0 : | check product (expr a*b) square meters | |
| 3660.0 : | product from algorithm square meters |
Testcase 3
| table 3 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 3601.0 : | long side meters | |
| 3600.0 : | short front side meters | |
| 1.0 : | optional meters | |
| 1.00027 : | answers: ratio long over short | |
| 12963600.25 : | squared term1 | |
| 0.25 : | squared term2 | |
| 12963600.0 : | check product (expr a*b) square meters | |
| 12963600.0 : | product from algorithm square meters |
Screenshots Section
figure 1. Calculator Screenshot
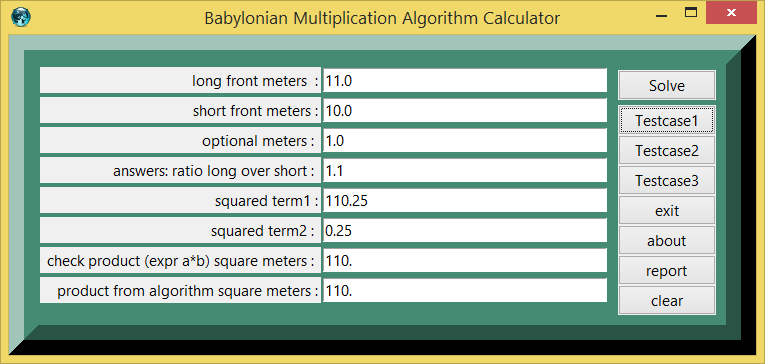
figure 2. Console Screenshot
--- 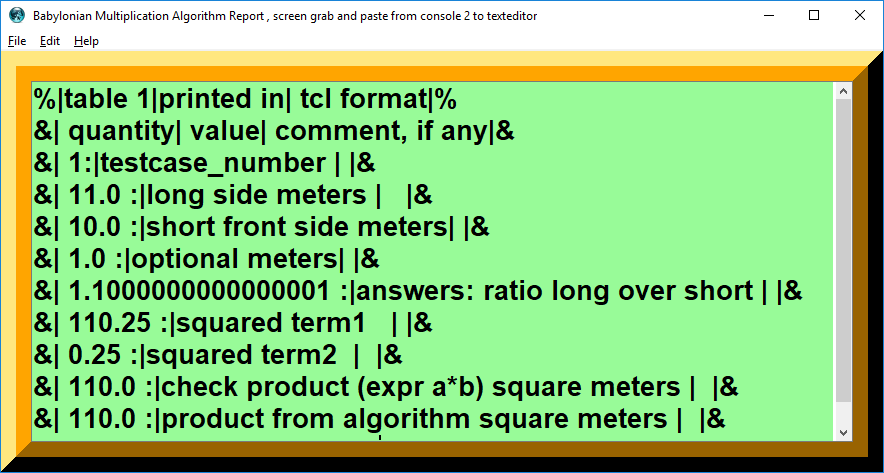
figure 3. Favorite Bablylonian Rectangle on Geometry Grid, includes (3-4-5)* (1/4) triangle
References:
- Primary references, Google <Babylonian Multiplication by M. Lewinter and W. Widulski>
- Amazing-Traces-of-a-Babylonian-Origin-in-Greek-Mathematics,
- Joran Friberg. Primary reference
- google < Babylonian trapezoid Wikipedia >
- Wikipedia search engine < quarter square multiplication algorithm >
- Wikipedia search engine < multiplication algorithm > Primary reference
- Wikipedia search engine < Babylonian Math >
- Wikipedia search engine < history of logarithms >
- Wikipedia search engine <Mesopotamian unit measurement >
- Wolfram Alpha search engine < trapezoid >
- Ancient Babylonian Algorithms, Donald E. Knuth, Stanford University
- Category Algorithm
- A Remarkable Collection of Babylonian Mathematical Texts, Joran Friberg, 2007
- Chalmers University of Technology Gothenburg, Sweden
- Joran Friberg and andrew george,
- Six more mathematical cuneiform texts in the Schoyen collection, MS 3895,
- Amazing Traces of a Babylonian Origin in Greek Mathematics,
- Joran Friberg
- A Remarkable Collection of Babylonian Mathematical Texts:
- Manuscripts in the Schøyen Collection: Cuneiform Texts I},
- Joran Friberg
- New-Mathematical-Cuneiform-Texts, by Joran Friberg
- and Farouk N.H. Al-Rawi
- Quarter Tables Revisited: Earlier Tables, Division of Labor in Table Construction, and Later
- Implementations in Analog Computers, primary reference.
- 2007 paper of David McFarland
- Yvonne Dold-Samplonius et al (eds), From China to Paris: 2000 Years
- Transmission of Mathematical Ideas. (Boethius, 46). Stuttgart: Steiner, 2002.
- web posting by rjlipton, Logarithms, Tables, and Babylonians, dec7,21010,very good ref.
- Neugebauer and Sachs, discussions, Tablet CBS-1535, in the Catalog of the Babylonian
- Section, University of Pennsylvania Museum
- A reconstruction of Plassmann’s table of quarter-squares (1933),
- Denis Roegel
- A Digital Quarter Square Multiplier, Everett Johnson, IEE Transactions , vol-29,n0 3, 3mar1980
- Mathematics-in-Ancient-Iraq-A-Social-History, E. Robson
- Neugebauer, Otto, and A. Sachs 1945. Mathematical
- Cuneiform Texts. New Haven: American Oriental Society.m 25, page34
- Reference to Tablet CBS-1535 as "squares table"
- Glaisher wrote important articles on quarter-squares.
- Sumerian Surveyor Area Formula and eTCL Slot Calculator Demo Example, numerical analysis
- precision math procedure used in TCL calculator Arjen Markus AM
- Computers and real numbers
- Floating-point formatting
Pseudocode & Equations Section
more than one formula for 1) tables and 2) calculator shell
Babylonian multiplication rule a * b = ((a + b)/2)^2 - ((a - b)/2)^2 # used in calculator shell
conventional Western formula for quarter square multiplication tables
is a * b= (1/4)*(((a+b)**2) - ( (a-b)**2 ) ) # used in Western tables circa 1600 to 1950 CE.
quarter square multiplication formula for the tables
is x*y = <.25* (x+y)**2> * <.25* (x-y)**2>.
# recommended, avoids division by zero
half square multiplication formula for the tables
may be equivalent to x*y = 0.5* <.5* (x+y)**2> * <.5* (x-y)**2> # used in tables,
# recommended, avoids division by zero
modern extension to the Babylonian multiplication algorithm
from the binomial theorem is a*b = 0.5*{a+b)**2 -a**2-b**2} # considered for calculator shell
a * b = expr { $a * $b } # TCL math.c call for check answer
QS(N) = (1/4) * N**2 , or 0.25 * N**2, or int’ed [ int [ expr 0.25*$N**2]]
HS(N) = (1/2) * N**2 , or 0.5 * N**2, or int’ed [ int [ expr 0.5*$N**2 ]]
approximate Babylonian quadrilateral formula expr <((a+c)/2) *((b+d)/2) > (not exact!!!)
product of 50*40*30 using modern base_60 logarithms, # used in thinking pod
the sum of logs is expr { 0.95546+0.90096+0.830706} , 2.687126.
The antilog in base_60 is expr 60**2.687126= 59995.193.
For the tables, the int function is used to clip remainders to integers.
the precision function by [AM] is used occasionally, but not every time.
note: mental and undocumented components in the Babylonian multiplication methods.
# exponent/ logarithm expressions
log (sqrt (m)) = (1/2)*log (m)
log (crt (m)) = (1/3)*log (m)
log (sqrt (m)) = (1/2)*log (m)
(1/2) = log (sqrt (m)) / log (m)
(1/2) = log (sqrt (m)) - (m))
log (crt (m)) = (1/3)*log (m)
(1/3) = log (crt (m)) / log (m)
(1/3) = log (crt (m)) - (m))
(1/2) = log (sqrt (m)) / log (m)
(2/1) = log (m) / log (sqrt (m))
2 = log (m - (sqrt (m))
(3/1) = log (m) / log (crt (m))
3 = log (m - (crt (m))
N = log (m - (N’rt(m))
N+1 = log (m - ((N+1)’rt(m))
log2 defined as ln N / ln 2 ,
log2 N =~ 1.442695 * ln N
log2 N =~ 3.321928 * log10 NAppendix Code
Trial Multiplication Calculator Shell
######)))))) TCL source code follows
# Babylonian Multiplication Algorithm calculator
# written on Windows XP on TCL
# working under TCL version 8.6
# This code is copyrighted same as TCL version 8.6
# 5nov2018 copyrighted under and same as TCL license.
# Editorial rights are reserved under TCL license
# gold on TCL club, 5nov2018
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} { long side meters :} }
lappend names { short front side meters :}
lappend names { optional meters : }
lappend names { answers: ratio long over short : }
lappend names { squared term1 :}
lappend names { squared term2 : }
lappend names { check product (expr a*b) square meters : }
lappend names { product from algorithm square meters :}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Babylonian Multiplication Algorithm
from TCL "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg "Calculator for Babylonian Multiplication Algorithms V2
from TCL ,
# self help listing
# 3 givens follow.
1) long_side length meters
2) short_side length meters
3) optional meters, not used yet
The Babylonian solution from the clay tablets
is genuine antique method from 1600 BCE
and different looking from some modern math methods.
# The Babylonians did not use modern algebraic notation,
# so the reader will have to bear some anachronisms in the TCL code.
# Comparing conventional formula(s) for product or area
# to Babylonian quarter square multiplication algorithm.
# For comparision, code will include redundant paths & formulas
# to compute result. The calculator uses modern units as meters and
# square meters for convenience to modern users and textbooks.
# Any convenient and consistent in/output units might be used
# like inches, feet, nindas, cubits, or dollars to donuts.
# Equations
# more than one formula for 1) QS() and HS() tables and 2) calculator shell
1) rule a * b = ((a + b)/2)^2 - ((a - b)/2)^2 # used in calculator shell
2) x * y = 0.5* <.5* (x+y)**2> * <.5* (x-y)**2> # used in half squares HS tables
3) a * b = (1/4)*(((a+b)**2) - ( (a-b)**2 )) # used in Western QS tables
4) a * b = 0.5*{a+b)**2 -a**2-b**2} # from the Western binomial theorem
The Babylonian mathematicians used base_60 notation,
but the algorithm steps, notation, and desired goal
can be transformed into base 10, base 16, etc for modern computers.
# Recommended procedure is push testcase and fill frame,
# change first three entries etc, push solve,
# and then push report. Report allows copy and paste
# from console to conventional texteditor. For testcases,
# testcase number is internal to the calculator and
# will not be printed until the report button is pushed
# for the current result numbers.
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK 8.6 license terms.
# Editorial rights retained under the TCL/TK license terms
# and will be defended as necessary in court.
Conventional text editor formulas or grabbed from internet
screens can be pasted into green console window.
Try copy and paste following into green screen console
set answer [* 1. 2. 3. 4. 5. ] # returns 120
# gold on TCL Club, 10aug2018 "
tk_messageBox -title "About" -message $msg }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set long_side $side1
set short_front_side $side2
set height $side3
# babylonian multiplication rule a * b = ((a + b)/2)^2 - ((a - b)/2)^2
set term1 [* [+ $long_side $short_front_side ] .5 ]
set term1 [** $term1 2 ]
set term2 [* [- $long_side $short_front_side ] .5 ]
set term2 [** $term2 2 ]
# babylonian mathematician uses table lookup here
set algorithm_result [- $term1 $term2 ]
set check_product_tcl [expr { $long_side * $short_front_side }]
set ratio_long_over_short [/ $long_side $short_front_side ]
set side4 $ratio_long_over_short
set side5 $term1
set side6 $term2
set side7 $check_product_tcl
set side8 $algorithm_result
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number reference_factor flag
console show;
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Babylonian Multiplication Algorithm Report , screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts "%|table $testcase_number|printed in| tcl format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |& "
puts "&| $side1 :|long side meters | |&"
puts "&| $side2 :|short front side meters| |& "
puts "&| $side3 :|optional meters| |& "
puts "&| $side4 :|answers: ratio long over short | |&"
puts "&| $side5 :|squared term1 | |&"
puts "&| $side6 :|squared term2 | |&"
puts "&| $side7 :|check product (expr a*b) square meters | |&"
puts "&| $side8 :|product from algorithm square meters | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 11.0 10.0 1.0 1.1 110.25 0.25 110. 110.}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 61. 60. 1. 1.01 3660.25 0.25 3660. 3660. }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 3601.0 3600.0 1.0 1.0001 12963600.0 0.25 12963600. 12963600.0 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .self_help -text self_help -command {self_help}
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Babylonian Multiplication Algorithm Calculator"
# end of file
# gold on TCL club, 5nov2018
# This posting, prose, screenshots, and TCL source code is
# copyrighted under the TCL/TK license terms.
# Editorial rights and disclaimers retained
# under the TCL/TK license terms
# and will be defended as necessary in court.
# end of file appendix : Script on Tables for TCL console
# pretty print from autoindent and ased editor
# Babylonian Quarter Squares Tables
# written on Windows XP on TCL
# working under TCL version 8.6
# gold on TCL, 10oct2018
wm title . "Babylonian Quarter Squares Tables"
namespace path {::tcl::mathop ::tcl::mathfunc}
set tclprecision 17
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . "Babylonian Quarter Squares Tables , cut and paste from console 2"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
proc precisionx {precision float} {
# tcl:wiki:Floating-point formatting, <AM>
# select numbers only, not used on every number.
set x [ expr {round( 10 ** $precision * $float) / (10.0 ** $precision)} ]
# rounded or clipped to nearest 5ird significant figure
set x [ format "%#.5g" $x ]
return $x
}
proc list_quarter_squares { aa bb} {
for {set i $aa} {$i<=$bb} {incr i} {
puts " &| $i | [ precisionx 3 [ int [* .25 $i $i] ] ] | |& "; }
return 1}
proc list_half_squares { aa bb} {
for {set i $aa} {$i<=$bb} {incr i } {
puts " &| $i | [ precisionx 3 [ int [* .5 $i $i] ] ] | |& ";
puts " &| [+ $i .5 ] | [ precisionx 3 [ int [* .5 [+ $i .5] [+ $i .5] ] ] ] | |& ";}
return 1}
proc list_binomial_theorem { aa bb} {
for {set i $aa} {$i<=$bb} {incr i} {
set a $i
set b $i
puts " &| $i | [ precisionx 3 [expr { 0.5*(($a+$b)**2-$a**2-$b**2) } ] ] | |& "; }
return 1}
set testcase_number 1
puts "%|Table $testcase_number: Babylonian Quarter Squares Tables |printed in| tcl format|% "
puts "%|N | int <N*N*.25> | comments if any|% "
list_quarter_squares 0 18
set testcase_number 2
puts "%|Table $testcase_number: Babylonian Half Squares Tables |printed in| tcl format|% "
puts "%|N | int <N*N*.5> | comments if any|% "
list_half_squares 0 20
set testcase_number 3
puts "%|Table $testcase_number: Binomial_Theorem Squares Tables |printed in| tcl format|% "
puts "%|a | a*a from subbing a*b = 0.5*(a+b)**2 -a**2-b**2) | comments if any |% "
list_binomial_theorem 0 10
# gold on TCL Club, 10oct2018
# This posting, prose, screenshots, and TCL source code is
# copyrighted under the TCL/TK license terms.
# Editorial rights and disclaimers retained
# under the TCL/TK license terms
# and will be defended as necessary in court.
# end of fileappendix, Golden Rectangle Dimensions for even numbered area units (burs)
golden rectangle ratio for 2 bur units
short_side_S*long_side_L = 2 bur in golden rectangle ratio
(1*S)*(1.61803*S)=expr 2*1800 # 4 bur
1.61803*(S**2)=3600 sq nindas
S**2= expr { 3600./1.61803 }
set S [expr { sqrt (2224.927) }]
S=47.169, L = 76.321 from expr { 1.61803*47.169}
check expr {47.169*76.321 } = 3599.985 square nindas
rectangle 4:3 side ratio, Length width in classic ratio.
1_15 or 1+1/4 in table of coefficient of the diagonal of length and width
a 3:4:5 rule with constant differences.
average=( L+W)/2 , deviation= (L-W)/2 golden rectangle ratio for 4 bur units
short_side_S*long_side_L = 4 bur in golden rectangle ratio
(1*S)*(1.61803*S)=expr 4*1800 # 4 bur
1.61803*(S**2)=7200 sq nindas
S**2= expr { 7200./1.61803 }
set S [expr { sqrt 4449.855 }]
S=66.7, L = 107.922 from expr { 1.61803*66.7}
check expr {66.7*107.922 } = 7198.3974 square nindasComments Section
Please place any comments here with your wiki MONIKER and dates, Thanks,gold12DEC2018
gold 9/27/2021. Switched some comment signs ;# to #. This a big file. Check earlier editions, if not compatible. Maybe obvious, but this page was written on Windows10 Tcl ports including ActiveTCL. I assume that the reader can cut and paste on screen, what the reader needs, and tootle on to his own project and own contribution pages to the TCL Wiki.