Chinese Horse Race Problems from Suanshu, DFP, and example eTCL demo calculator, numerical analysis
Chinese Horse Race Problems from Suanshu, Double False Position Algorithm, and eTCL demo example calculator, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 12dec2018
- Chinese Horse Race Problems from Suanshu, Double False Position Algorithm, and eTCL demo example calculator, numerical analysis
- Pseudocode Section
- Appendix Code
- CVS Spreadsheet for Charted Graphical Solution
- test of Chinese font for Suanshu horse problem 19 of section 7
- Comments Section
Introduction
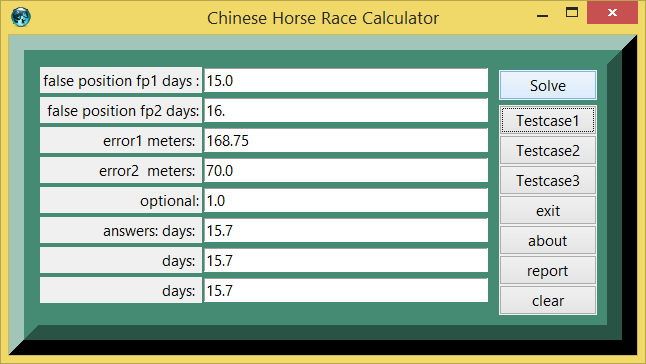
gold Here is some eTCL starter code for Chinese Horse Race Problems from Suanshu and double false position algorithm (DFP) in calculator shell.
Setting up the horse race problem
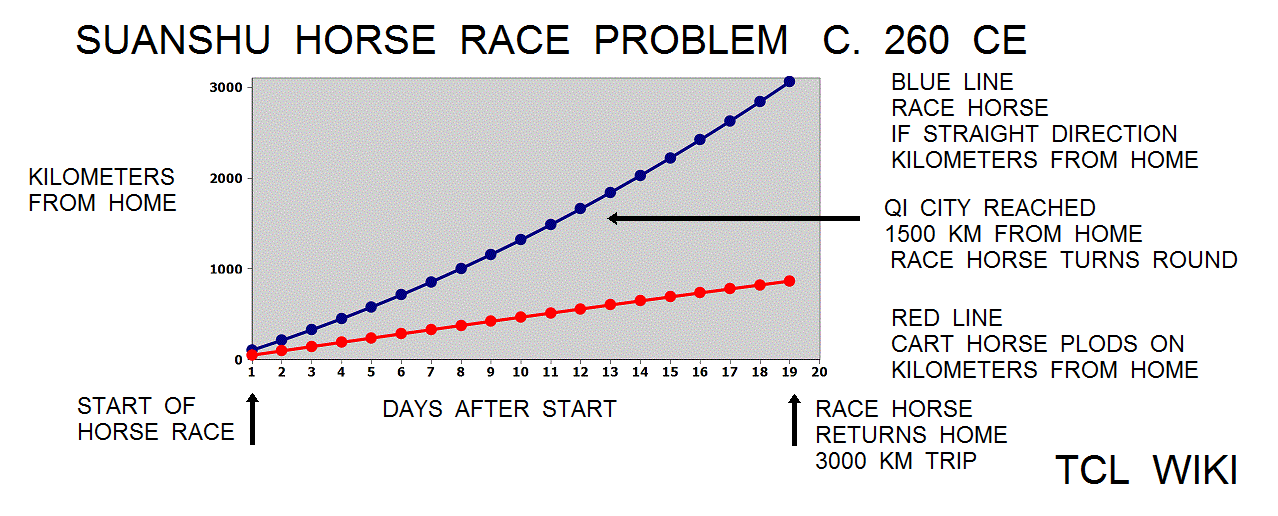
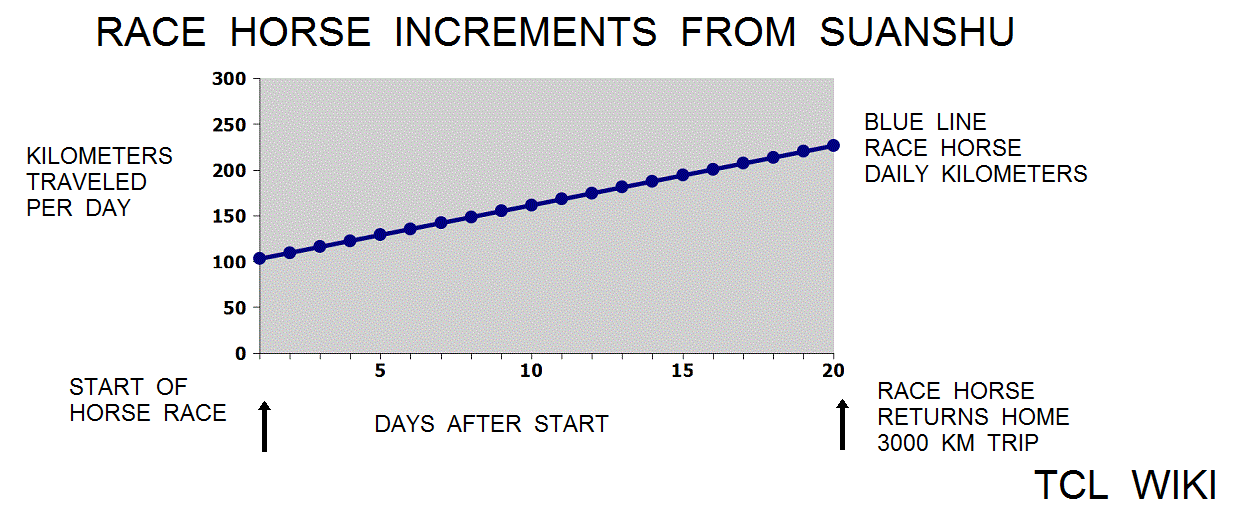
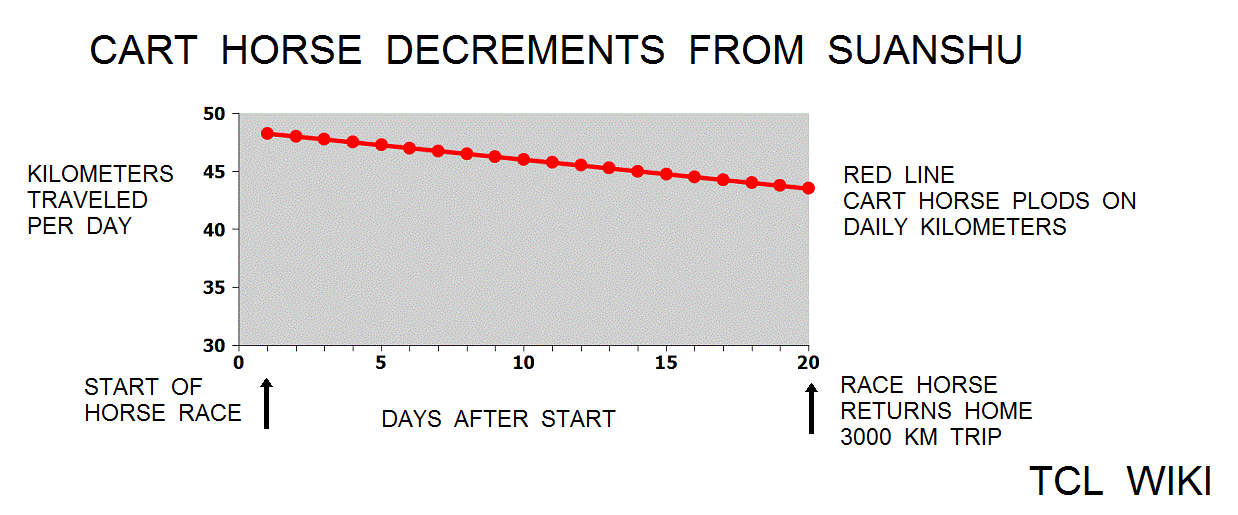
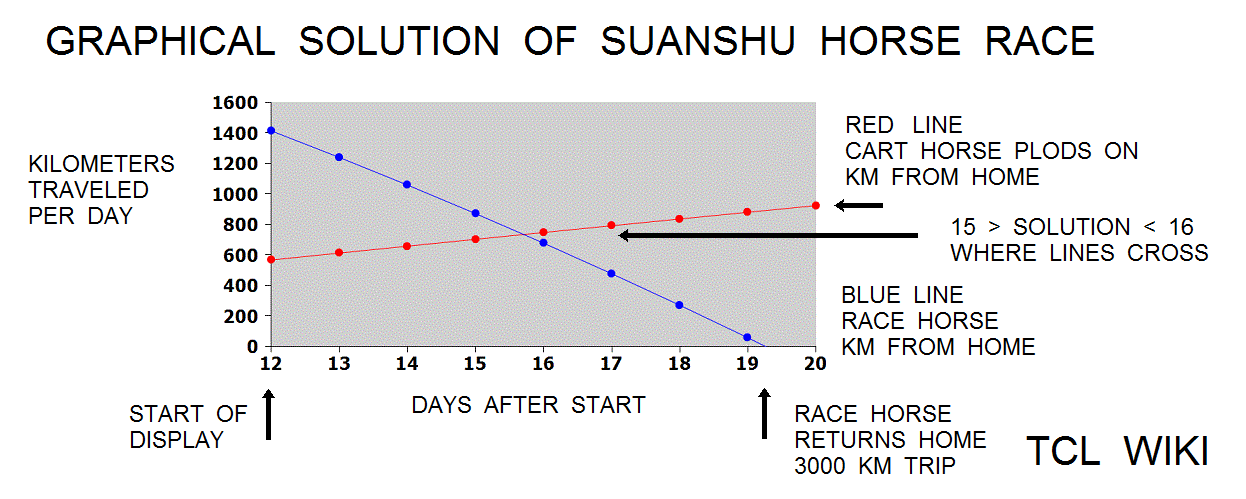
The Chinese used double false position (DFP) to interpolate the solution of a horse race problem in the Suanshu or Nine Chapters (commentary c. 260 CE). For the eTCL console program below, the Chinese miles (li) were converted to kilometers, using the modern .5 km per li constant (since there is some uncertaincy about the Suanshu equivalent miles). The paraphrased horse race problem largely follows the account of Swartz and Shen. A race was staged between a racehorse and a cart horse with a two wheeled cart to Qi City and return. The distance between the Changan home to Qi City is 1500 km. The racehorse has a pace of 96.5 km on the first day and has an increment of 6.5 km each day. The pace of the cart horse is 48.5 and has a decrement of 0.25 km each day. The race horse reaches Qi City first and turns home. Meanwhile the cart horse continues on the road. On what day will the very tired cart horse and returning racehorse meet?
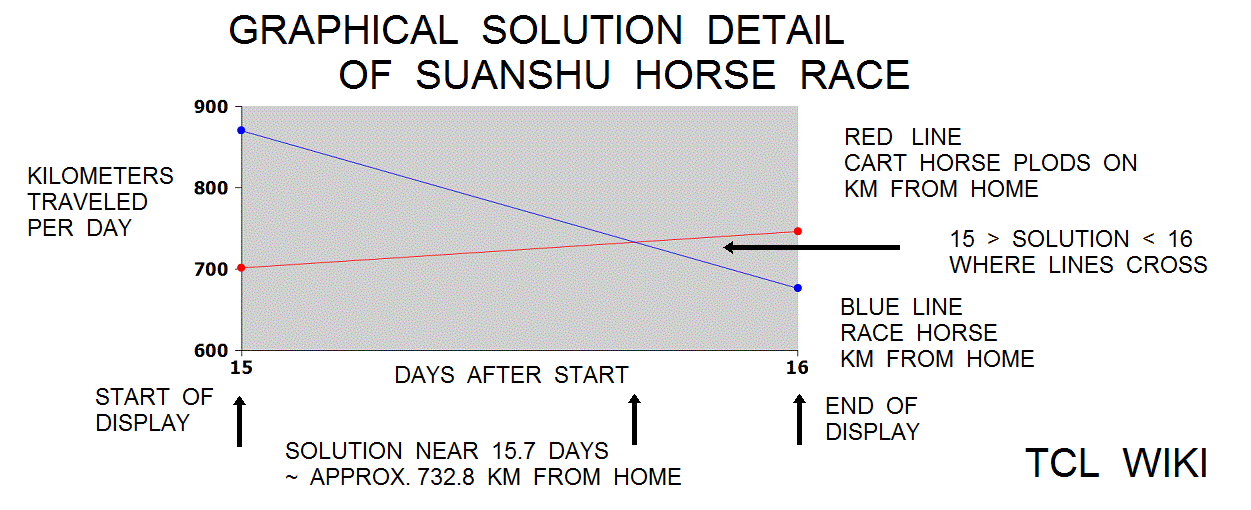
To reach the same solution as the Suanshu, considerations are dependent on how the Suanshu counts days, nightwatches, and daily travel. For timing around the day interval of the horse race solution, it is convenient to use sunrise and sunset as watches or interval breakpoints. Each 24 hour day, the horses start about 1/4 or 0.25 day and rest beginning about 3/4 or 0.75 day. At sunset of day 15, the cart horse is 701.25 km from home and the returning racehorse is 870 km from home. The separation of the cart horse and racehorse is 870-701.25 or 168.75 km apart. Whether considering alone the current pace of the racehorse 193.5 km over the 15th day interval or the combined pace of both horses on the 15th (193.5 km and 44.25 km over the interval), the solution can be expected on the next day or the 16th interval. In other modern terms, the horse race solution is bounded 15 > solution < 16 days, calling for a piecewise linear solution to estimate the fraction.
Suanshu Solution
The Suanshu solution was 15+ 135/191 or decimal 15.7068 days, ref Shen et al. At sunrise of day 16 (~ 16.25), the horses wake up and continue the race from the conditions of the previous sunset, the cart horse is 701.25 km from home and the returning racehorse is 870 km from home. Both horses have a different and separate paces for the 16th day, but at sunset (~ 16.75) the returning racehorse is 676 km from home and the cart horse is 746 km from home. Clearly, the horses have passed each other between sunrise and sunset on the 16th day interval. On the 16th, the separation of the cart horse and racehorse is 746-676 or 70 km apart. The days 15 and 16 are loaded as the false positions. The error1 is 168.75 km and error2 is 70 km. As a trial calculation, the DFP solution approximates (fp1*e2+ fp2*e1) / (e2+e1), substituting expr (15.*70.+ 16.*168.75) / (168.75+70.) 15.7068 days.
Since the preparations for the DFP solution involve adding and subtracting over 16 intervals of fractions, there is ample chance for miscues on the exact solution. The increment on the racehorse is expr((96.5+6.5))/96.5-1 or 0.06735, about 6.7 percent each day. The decrement on the cart horse is exp r((48.5+.25))/48.5-1 or 0.00515, about 0.5 percent each day.The combined error on the eTCL solution, DFP, and hand calculations for the horse race problem would probably be about +- 3 percent relative error. The horse race problem has some analogies to the some lunar eclipse problems, ie. the apparent position of the moon "chasing" and eclipsing the sun etc. Since loading the specific false positions and DFD formula is critical for the Chinese problems, maybe the eTCL logic switch should be modified to allow direct loading of the false positions or errors.
The Suanshu uses an indirect stage from direct questions (leap frog) or black boxes the error terms in modern terminology. Since this indirect stage of DFP problems is tricky, one can see why the some much later European works and even translations copied the easy stuff and dropped the indirect DFP methods in the Suanshu. Clearly, the available problems in the Suanshu show the versatility of the double false position method from joint purchases to horse races.
Setting Calculator Conditions
In the eTCL calculator, two false positions are supplied as guesses.
The DFP logic switch is usually set to 1. Set DFP logic switch 1 for ++ false position errors, 2 for +-, 3 for --, or 4 for negative false position (override) entries. The DFP logic switches 2,3,4 check the calculator results for the Chinese and Arabian variant problems, which may generate negative e1&e2 and negative error sums.
Conclusions
The eTCL calculator seems to be working very well, getting a correct solution even with (override) negative entries.
| Mixed Signs and Logic Switches for DFP errors e1&e2 | tcl wiki format | ||
|---|---|---|---|
| quantity | value | comment, if any | |
| ++ : | double surplus | condition +e2>+e1, gets positive error | |
| +-: | mixed surplus deficit | condition +e2>(-e1), gets positive error | |
| -+: | mixed deficit surplus | condition (-e2)>+e1, gets negative error | |
| --: | double deficit | condition -e2>-e1, gets negative error | |
| ++ : | double surplus | set false_position_1 (int (* $side_length (/ 4. 5. ))) | |
| ++ : | double surplus | set false_position_1 (int (* $side_length (/ 3. 5. ))) | |
| +-: | mixed surplus deficit | set false_position_2 (int [* $side_length (/ 6. 4. ))) | |
| +-: | mixed surplus deficit | set false_position_2 (int [* $side_length (/ 3. 4. ))) | |
| --: | double deficit | set false_position_1 (int (* $side_length (/ 8. 4. ))) | |
| --: | double deficit | set false_position_2 (int (* $side_length (/ 6. 4. ))) | |
| note : | calculator works if negative errors generated | ||
| but neg e1&e2 and error sum caused terminology & varients in early times | |||
| eTCL logic can be changed for generating neg e1&e2 |
Pseudocode Section
# using pseudocode
# possible problem instances,
initialize algorithm_result = 1.
set false1 [expr guess * 3/5]
set false1 [expr guess * 4/5]
calculate f(false1) and f(false2)
error1 = product -f1
error2 = product -f2
[expr (e2*f1-e1*f2)/(e2-e1)]
check algorithm
f(solution) =? initial product
check_sum = a+b+c+d+e = original real estate
set answers and printout with resulting values
pseudocode: need test cases > small,medium, giant
pseudocode: need testcases within range of expected operation.
pseudocode: are there any cases too small or large to be solved?Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
Testcase 1
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 15.0 : | false position fp1 days | |
| 16.0 : | false position fp2 days | |
| 168.75 : | error1 meters | |
| 70.0 : | error2 meters | |
| 1.0 : | optional logic switch | |
| 15.7068 : | answers: days | |
| 15.7068 : | days | |
| 15.7068 : | days |
Testcase 2
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 10.0 : | false position fp1 days | |
| 20.0 : | false position fp2 days | |
| 100.0 : | error1 meters | |
| 120.0 : | error2 meters | |
| 1.0 : | optional logic switch | |
| 14.545 : | answers: days | |
| 14.545 : | days | |
| 14.545 : | days |
Testcase 3
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 15.0 : | false position fp1 days | |
| 25.0 : | false position fp2 days | |
| 120.0 : | error1 meters | |
| 150.0 : | error2 meters | |
| 1.0 : | optional logic switch | |
| 19.444 : | answers: days | |
| 19.444 : | days | |
| 19.444 : | days |
Screenshots Section
figure 1.
figure 2.
figure 3.
figure 4.
figure 5.
figure 6.
References:
- Horseracing in Tcl by RS
- Ancient Egyptian Double False Position Algorithm, and example eTCL demo calculator, numerical analysis
- Les neuf chapitres : le classique mathématique de la Chine
- ancienne et ses commentaires , in French and Chinese
- author(s) Karine Chemla, Guo Shuchun
- historia mathematica 1 (1974), 47-64
- yang hui's commentary on the increase and decrease chapter of Suanshu
- by lam lay yong, university of singapore
- Suanshu English translation: Florian Cajori: Arithmetic in Nine Sections, 1893.
- Suanshu English translation: Lam Lay Yong: Jiu Zhang Suanshu,
- A Suanshu Overview, Archive for History of Exact Science, 1994
- Nine Chapters and Liu Hui's commentary,
- Nine Chapters on the Mathematical Art, Shen, Oxford 1999
- The Suanshu, Notes on Nine Chapters, Draft Notes. C. Cullen 2004
- Issues in the Origin and Development of Hisab al-Khata’ayn
- (Calculation by Double False Position), Randy K. Schwartz ,
- Eighth North African Meeting on the History of Arab Mathematics
- Analysis of ancient Chinese horse race problem,
- Mingming Leng, Mahmut Parlar1,
- DeGroote School of Business, McMaster University, Hamilton, Ont., Canada
- 10 December 2004
- On Generalized Tian Ji’s Horse Racing Strategy,
- Jian-Jun SHU School of Mechanical & Aerospace Engineering,
- Nanyang Technological University, 50 Nanyang Avenue, Singapore
- A Remarkable Collection of Babylonian Mathematical Texts, Joran Friberg,
- Chalmers University of Technology, Gothenburg, Sweden
- (major work on Babylonian inheritance problems)
- Muroi, Kazuo (1988). Inheritance problems of Babylonian mathematics.
- Historia Scientiarum , 34, 11-19
- Chabert, J. "Methods of False Position." Ch. 3 in A History of Algorithms: From the Pebble to the Microchip. , 1999.
- John Hannah , False position in Leonardo of Pisa's Liber Abbaci,Historia Mathematica Volume 34 issue 3 2007
- Eugene C. Boman,False Position, Double False Position and Cramer's Rule, College Mathematics Journal
- Howard Eves ,On the practicality of the rule of false position, Mathematics Teacher Volume 51
- Joy B. Easton, the rule of double false position, Mathematics Teacher Volume 60
- Vera Sanford, the rule of false position, Mathematics Teacher Volume 44 issue 5 1951
- Karine Chemla, Reflections on the World-wide History of the Rule of False Double Position, or: How a Loop Was Closed
- Thomas G. Edwards -- Using the Ancient Method of False Position to Find Solutions, Mathematics Teaching in the Middle School Volume 14 issue 4 2008
- Oneliner's Pie in the Sky
- One Liners
- Category Algorithm
- Babylonian Number Series and eTCL demo example calculator
- Brahmagupta Area of Cyclic Quadrilateral and eTCL demo example calculator
- Gauss Approximate Number of Primes and eTCL demo example calculator
- Land surveying in ancient Mesopotamia, M. A. R. Cooper
- Sumerian Approximate Area Quadrilateral and eTCL Slot Calculator Demo Example , numerical analysis
- Thomas G. Edwards, Using the Ancient Method of False Position to Find Solutions
- Joy B. Easton, rule of double false position
- Vera Sanford, rule of false position
Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# Approximate Chinese horse race calculator
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI, 20feb2017
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {false position fp1 days :} }
lappend names {false position fp2 days:}
lappend names {error1 meters: }
lappend names {error2 meters: }
lappend names {optional:}
lappend names {answers: days: }
lappend names {days: }
lappend names {days: }
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Chinese Horse Race
from TCL WIKI,
written on eTCL "
tk_messageBox -title "About" -message $msg }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8 flag
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set false_postion1 $side1
set false_postion2 $side2
set error1 $side3
set error2 $side4
# initialize solution variable
set solution_days 1
set solution_days [+ [* $false_postion1 $error2 ] [* $false_postion2 $error1 ]]
set solution_days [/ $solution_days [+ $error2 $error1 ]]
set flag 1
set side6 $solution_days
set side7 $solution_days
set side8 $solution_days
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number flag
console show;
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |& "
puts "&| $side1 :|false position fp1 days| |&"
puts "&| $side2 :|false position fp2 days | |& "
puts "&| $side3 :|error1 meters | |& "
puts "&| $side4 :|error2 meters | |&"
puts "&| $side5 :|optional logic switch | |&"
puts "&| $side6 :|answers:days | |&"
puts "&| $side7 :|days | |&"
puts "&| $side8 :|days | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 15.0 16. 168.75 70.0 1.0 15.7 15.7 15.7}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 10.0 20.0 100.0 120.0 1.0 14.5 14.5 14.5 }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 15.0 25. 120.0 150.0 1.0 19.5 19.5 19.5 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Chinese Horse Race Calculator" Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
Chinese Horse Race Problem from Nine Chapters (commentary c.260 CE )
# pretty print from autoindent and ased editor
# initial console program, Chinese horse race problem
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI, 10feb2017
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
console show
set race_distance 96.5
#set china_distance 1500.
set china_distance 1500.
set good_horse_pace 96.5
set good_horse_increment 6.5
set cart_horse 48.5
set cart_horse_decrement 0.25
set good_horse_distance 96.5
set cart_horse_distance 48.5
set cart_horse_distance 48.5
set good_horse_tally 96.5
set cart_horse_tally 48.5
set cart_horse_tallyx 0
set horse_race_days 1
set distance_from_home 0
set i 25
while {$i>0} {
set race_distance [+ $race_distance [* $race_distance $good_horse_increment]]
if { $horse_race_days > 25 } { break }
puts "$horse_race_days , $good_horse_tally, $cart_horse_tally , $good_horse_distance , $cart_horse_distance , $distance_from_home "
set good_horse_distance [+ $good_horse_distance $good_horse_increment ]
#set cart_horse_distance [- $cart_horse_distance $cart_horse_decrement ]
set cart_horse_distance [- $cart_horse_distance $cart_horse_decrement]
set good_horse_tally [+ $good_horse_tally $good_horse_distance ]
set cart_horse_tally [+ $cart_horse_tally $cart_horse_distance]
set cart_horse_tallyx [- 1500 $cart_horse_tally]
if { $good_horse_tally > 1500 } { set distance_from_home [- 1500 [- $good_horse_tally 1500]]}
incr horse_race_days 1
#incr good_horse_distance 1
#incr cart_horse_distance 1
incr i -1
}
puts " &|$good_horse_tally | final good_horse_tally km | | ||&"
puts " &|$cart_horse_tally | final cart_horse_tally km | | ||&"
puts " &|$horse_race_days | final horse_race_days | | |&"
puts " &|$horse_race_days | final horse_race_days | | ||&"
puts " &|$horse_race_days | upper bound is average + .5*average | | |&"
puts " &|$horse_race_days | hold: lower bound is average - .5*average | | ||&"
puts " &|$horse_race_days | bound:: constant distance or slot | | ||&" CVS Spreadsheet for Charted Graphical Solution
0,Horse Race Problem 19/20 in Section 7 of Suanshu,,,, 1 , 96.5, 48.5 , 96.5 , 48.5 , 0 2 , 199.5, 96.75 , 103.0 , 48.25 , 0 3 , 309.0, 144.75 , 109.5 , 48.0 , 0 4 , 425.0, 192.5 , 116.0 , 47.75 , 0 5 , 547.5, 240.0 , 122.5 , 47.5 , 0 6 , 676.5, 287.25 , 129.0 , 47.25 , 0 7 , 812.0, 334.25 , 135.5 , 47.0 , 0 8 , 954.0, 381.0 , 142.0 , 46.75 , 0 9 , 1102.5, 427.5 , 148.5 , 46.5 , 0 10 , 1257.5, 473.75 , 155.0 , 46.25 , 0 ce11 , 1419.0, 519.75 , 161.5 , 46.0 , 0 12 , 1587.0, 565.5 , 168.0 , 45.75 , 1413.0 13 , 1761.5, 611.0 , 174.5 , 45.5 , 1238.5 14 , 1942.5, 656.25 , 181.0 , 45.25 , 1057.5 15 , 2130.0, 701.25 , 187.5 , 45.0 , 870.0 16 , 2324.0, 746.0 , 194.0 , 44.75 , 676.0 17 , 2524.5, 790.5 , 200.5 , 44.5 , 475.5 18 , 2731.5, 834.75 , 207.0 , 44.25 , 268.5 19 , 2945.0, 878.75 , 213.5 , 44.0 , 55.0 20 , 3165.0, 922.5 , 220.0 , 43.75 , -165.0
test of Chinese font for Suanshu horse problem 19 of section 7
listed as problem 20 by some authors
1)盈不足:
This problem deals with terms of lack and surplus.
2)今有良馬與駑馬發長安至齊。齊去長安三千里。
These were a good horse and unkempt mane {cart? nag?} horse
{traveling} from Changan to Qi City.
Qi City at a distance of three thousand miles
3)良馬初日行一百九十三里,日增十三里。駑馬初日行九十七里,
Good horse on the first day {travels} ninety three three units,
increasing thirteen units {each day}.
In early day of race, at the beginning of the day ninety seven,
{ Additional three 3 in Chinese
original text, but not understood here}
4)日減半里。良馬先至齊,復還迎駑馬。問幾何日相逢及各行幾何?
{Cart horse decreases by} half unit each day.
Good horse is first to Qi city,
and returns {to meet the cart?} horse.
Ask the geometric day to meet and the geometry of each track?
{geometric day may mean fraction? of a day}
5)答曰:一十五日、一百九十一分日之一百三十五而相逢。
Answer: At fifteen days, one hundred and
ninety one one hundred and thirty and five {horses} meet.
{Chinese fraction for solution, 15 + 135/191 days}
6)良馬行四千五百三十四里、一百九十一分里之四十六。
Good horse is four thousand five hundred thirty-four,
one hundred forty-one hundred forty-six units
{Chinese fraction for race horse, 4534 + 46/191 units}
7)駑馬行一千四百六十五里、一百九十一分里之一百四十五。
Four thousand four hundred and sixty five hundred miles,
one hundred and ninety one hundred and one hundred and forty five.
{Chinese fraction for cart horse, 1465+ 145/191 units }
8)術曰:假令十五日,不足三百三十七里半。令之十六日,多一百四十里。
scholar {Liu} said: leave fifteen days,
less than three hundred thirty-seven in half.
So that on the 16th, more than one hundred and forty miles.
{Chinese fraction for separation distance on 15th, 337 + 1/2 units }
{Chinese expression for separation distance on 16th, 140 units }
9)以盈、不足維乘假令之數,并而為實。并盈不足為法。
to surplus, lack of dimension by the number of instructions,
and for the real. And lack of profit for the law.
10)實如法而一,得日數。不盡者,以等數除之而命分。
the real law {and for the error party of } one, the number of days.
Not the other, in addition to the number of
#end of file
English paraphrases marked with brackets {}
paraphrased translation of race horse problem 19/20 from Suanshu
problem deals with terms of insufficient and surplus:
3 thousands li (Chinese miles),.
Liang Ma early June, increasing 193 pace intervals, 13 li increments .
In the early days of the cart horse,
decrements are less one half li (Chinese mile). Race horse first
Whether geometry, reunions and the line geometry?
What is the time of reunion?
answer is, {Chinese fraction} 191 units , day 135 and separated.
The starter line Lane, {Chinese fraction} 191 hours in 145.end of test
gold This page is copyrighted under the TCL/TK license terms, this license .
Comments Section
Please place any comments here, Thanks.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |