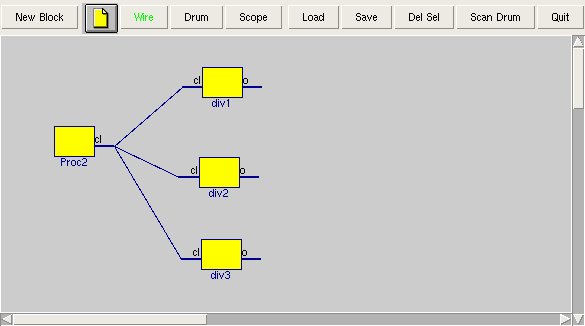
Clock divider BWise example
First my interests from the page about Network Theoretical Elements in Bwise and second the general interest raised about fundamental computer science (which I cannot help but see in the circuits, not the software) led to this examples of having something (a socket, a proc, a bwise block, an oscillator, a clock pulse) which generates a clock signal, which is a paced, repeated change, which feeds i this case 3 divider blocks to generate derived rates.
The generator in the example could be a high frequency generator, which is divided a few hundred times in the dvi1..3 blocks to generate square waves (most likely) which form a minor triad chord at their combined outputs. This happens to be an interesting software matter too, for instance for repeated servicing of times services, especially when they're fine grained.
A simple signal example assuming small binary divider ratio (of course appearing in computer circuits:
cl: | 0101010101010101010..
---------+--------------------
div1.o: | 0 1 0 1 0 1 0 1 0 1..
div2.o: | 0 0 1 0 0 1 0 0 1 0..
div3.o: | 0 0 1 1 0 0 1 1 0 0..
--> Time
In this signal diagram the div1 block divides by 2, the div2 block divides (necessarily asymmetrically) by three, and div3 is a four-divider, meaning their signal repeat in intervals of respectively 2, 3 or 4 input clock cycles. Of course Proc2 is the clock generator block.
To make the sound of a minor triad musical chord, the blocks would have to have frequencies which are like the C, Eb and G note, which can be relatively accurately achieved by choosing division factors in the order of a few hundred (9 or more bits dividers in hardware) to get the right frequencies with enough accuracy. In software, this is harder, because the call rate of the main clock procedure would be quite high.
For my example it is interesting to know how the clock is distributed, so where is the cl signal all connected to. In this case there is a standard bwise function to check where the pin cl.out is connected to (In FPGA's this would be interesting problem, too).
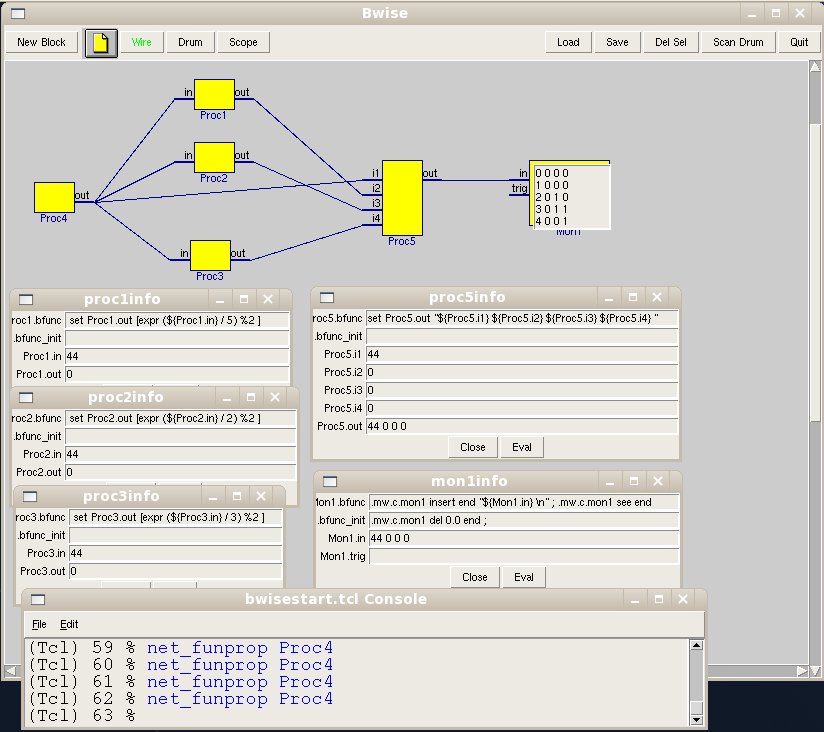
TV (dec 16, ' 08) An example with the block functions filled in:
# The blocks with creation coordinates
newproc {} {} in out 40 {} {} 243.0 123.0
newproc {} {} in out 40 {} {} 243.0 186.0
newproc {} {} in out 40 {} {} 239.0 284.0
newproc {} {} {} out 40 {} {} 83.0 226.0
newproc {} {} {i1 i2 i3 i4} out 40 {} {} 431.0 204.0
newmon 0 80 65 {} {} 578.0 204.0
# links
connect {} Proc4 out Proc1 in
connect {} Proc4 out Proc2 in
connect {} Proc4 out Proc3 in
connect {} Proc4 out Proc5 i1
connect {} Proc1 out Proc5 i2
connect {} Proc2 out Proc5 i3
connect {} Proc3 out Proc5 i4
connect {} Proc5 out Mon1 in
# Divide block functions
set Proc1.bfunc {set Proc1.out [expr (${Proc1.in} / 5) %2 ]}
set Proc2.bfunc {set Proc2.out [expr (${Proc2.in} / 2) %2 ]}
set Proc3.bfunc {set Proc3.out [expr (${Proc3.in} / 3) %2 ]}
set Proc5.bfunc {set Proc5.out "${Proc5.i1} ${Proc5.i2} ${Proc5.i3} ${Proc5.i4} "}
# Init main counter
set Proc4.out -1
# Set block execute function (incr counter) and init functions (reset counter)
set Proc4.bfunc {incr Proc4.out}
set Proc4.bfunc_init {set Proc4.out -1}
# Remove clear from monitor block, and make that the init function (see right click popup)
set Mon1.bfunc_init {.mw.c.mon1 del 0.0 end ;}
set Mon1.bfunc {.mw.c.mon1 insert end "${Mon1.in} \n" ; .mw.c.mon1 see end}
Now use Fun_prop from the right-clock popup menu on Proc4 or
net_funprop Proc4
repeatedly to advance the main counter, so that the derived dividers show their binary divide outputs in the mon window.
The above can be pasted in the console of a started up bwise and will give the working graph and the init menus working on the first (left) and last (right) blocks. This example if it is taken as a kind of logic simulation allows for setting the value Proc4.out which is the time value (for instance by using right click to open the blockinfo window) in integer time steps. Maybe the divide by and modulo 2 in the divider blocks (in the middle) gives rounding errors at some point.