Network Theoretical Elements in Bwise
by Theo Verelst
Network theory in the Electrical Engineering sense is the theory of electrical networks, like the practice is electronical networks with actual voltage supplies, resistors, capacitors, etc. Electrical network elements are like Platonic concepts of the electronical counterparts, where the main elements are sources (voltage or current), resistive elements, and complex resistive elements, inductances and capacitors.
Bwise is kind of inviting to use the Tk canvas to draw not blocks but network elements, and so to play with virtual electronics. In fact, when I worked at university I came up with the foundation of BWise for amoung other things such reason. I was Master of Science (close to getting a PhD) in Network Theory Section, and computers were getting good enough to use for complex networks being graphically respresented (as we know the father of tcl/tk, J. Oesterhout, invented the language amoung other reasons for yet another EE purpose: chip layer design).
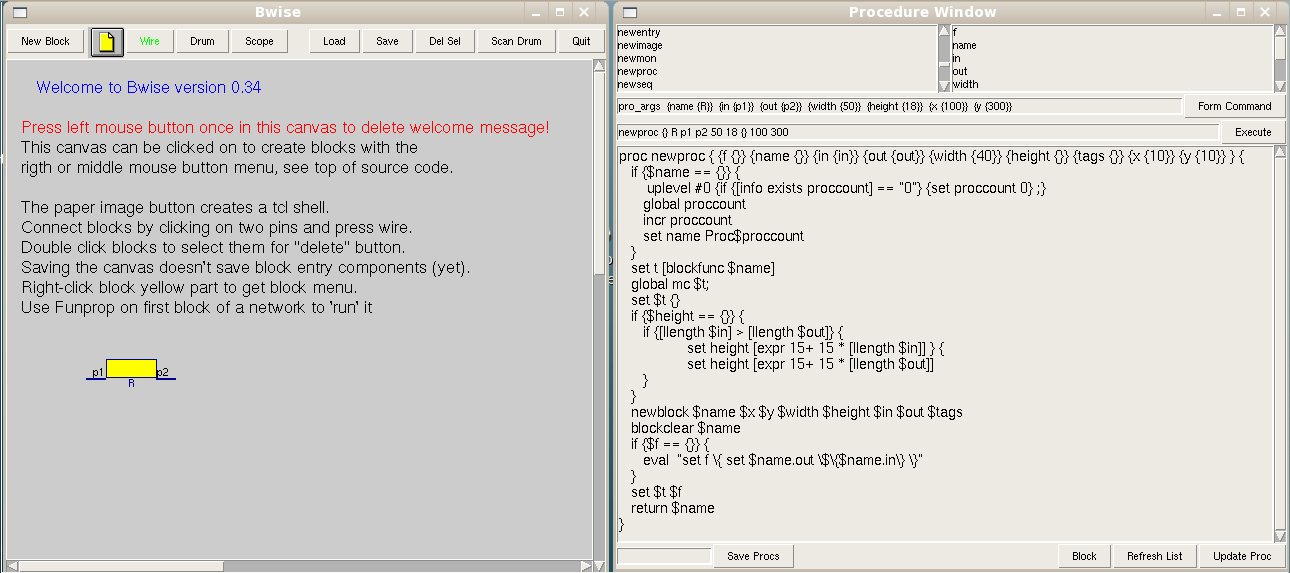
Bwise normally uses rectangular blocks as elements of its graph structure, in this case I want to adapt the routine for creating such blocks to create on the canvas another graphical representation, to begin with of a resistor, which is in fact also a rectangle, in two possible directions, so that shouldn't be too hard. Trying this with bwise by typing with the interactive command composer or in the console window
newproc {} R p1 p2 50 18 {} 100 300we see the graphics are not automcatically appealing:
So we have to make a new create command for bwise, which calls newblock with other parameters, or we should create a new procedure for newblock, to be able to use other colors and such.
Lets do that first, and then be able to play around with freshman year electrical networks, and be able to use more than a few bwise pages and ideas on various and tcl pages in the context. For instance driving maxima to actually compute what goes on in the networks, even symbolically, and some scripts to even make sounds of the result. Of course this is all the more fun when an interactive graphical representation such as in bwise with the Tk canvas is available.
Well, calling newblock to make a resistor block for us like so
newblock R1 200 300 50 18 p1 p2
also gives no good result, the pins aren't drawn nice, and maybe we want a black and white and transparent block instead anyhow, so lets make a new proc called newnetwelm
proc newnetwelm { {name {}} {x {0}} {y {0}} {type {R}} {moretags {}} } {
set w 50 ; set h 18 ; set pinsin p1 ; set pinsout p2
global bcount mw mc
if {$name == ""} {set name "R$bcount" ; set bcount [expr $bcount +1]}
eval $mc create rect $x $y [expr $x+$w] [expr $y+$h] -tags "{$name newblock block $moretags}" -fill \"\" -outline black
eval $mc create text [expr $x+$w/2] [expr $y+$h/2+1] -anchor c -text $name -fill darkblue -tags "{$name crb label $moretags}"
set ii 0
foreach i $pinsin {
eval $mc create text [expr $x-1] [expr $y+9+$ii] -anchor se -text $i -tags "{$name crb pinname $i $moretags}"
eval $mc create line [expr $x-20] [expr $y+10+$ii] [expr $x+0] [expr $y+10+$ii] -width 2 -fill darkblue -tags "{$name newblock pin $i typein $moretags}"
set ii [expr $ii+15]
}
set ii 0
foreach i $pinsout {
eval $mc create text [expr $x+$w+2] [expr $y+9+$ii] -anchor sw -text $i -tags "{$name crb pinname $i $moretags}"
eval $mc create line [expr $x+$w+20] [expr $y+10+$ii] [expr $x+$w+0] [expr $y+10+$ii] -width 2 -fill darkblue -tags "{$name newblock pin $i typeout $moretags}"
set ii [expr $ii+15]
}
}Which is quickly derived from newblock for now this procedure creates a resistor schematic symbol, in horizontal form, and the parameter type isn't checked yet:
After playing a little with the graphics (interpreted languages with graphics are fun!) I added a capacitor drawing:
proc newnetwelm { {name {}} {x {0}} {y {0}} {type {R}} {moretags {}} } {
global bcount mw mc
switch $type R {
set w 50 ; set h 18 ; set pinsin p1 ; set pinsout p2
if {$name == ""} {set name "R$bcount" ; set bcount [expr $bcount +1]}
eval $mc create rect $x $y [expr $x+$w] [expr $y+$h] -tags "{$name newblock block $moretags}" -fill \"\" -outline black
eval $mc create text [expr $x+$w/2] [expr $y+$h/2+1] -anchor c -text $name -fill darkblue -tags "{$name crb label $moretags}"
set ii 0
foreach i $pinsin {
eval $mc create text [expr $x-1] [expr $y+9+$ii] -anchor se -text $i -tags "{$name crb pinname $i $moretags}"
eval $mc create line [expr $x-20] [expr $y+10+$ii] [expr $x+0] [expr $y+10+$ii] -width 2 -fill darkblue -tags "{$name newblock pin $i typein $moretags}"
set ii [expr $ii+15]
}
set ii 0
foreach i $pinsout {
eval $mc create text [expr $x+$w+2] [expr $y+9+$ii] -anchor sw -text $i -tags "{$name crb pinname $i $moretags}"
eval $mc create line [expr $x+$w+20] [expr $y+10+$ii] [expr $x+$w+0] [expr $y+10+$ii] -width 2 -fill darkblue -tags "{$name newblock pin $i typeout $moretags}"
set ii [expr $ii+15]
}
} C {
set w 18 ; set h 27
if {$name == ""} {set name "C$bcount" ; set bcount [expr $bcount +1]}
eval $mc create rect $x $y [expr $x+$w/3] [expr $y+$h] -tags "{$name newblock block $moretags}" -fill black -outline black
eval $mc create rect [expr $x+$w*(2.0/3)] [expr $y] [expr $x+$w] [expr $y+$h] -tags "{$name newblock block $moretags}" -fill black -outline black
eval $mc create text [expr $x+$w/2] [expr $y+$h+1] -anchor n -text $name -fill darkblue -tags "{$name crb label $moretags}"
eval $mc create text [expr $x-1] [expr $y+$h/2-1] -anchor se -text p1 -tags "{$name crb pinname p1 $moretags}"
eval $mc create line [expr $x-20] [expr $y+$h/2] [expr $x+0] [expr $y+ $h/2] -width 2 -fill darkblue -tags "{$name newblock pin p1 typein $moretags}"
eval $mc create text [expr $x+$w+2] [expr $y+$h/2-1] -anchor sw -text p2 -tags "{$name crb pinname p2 $moretags}"
eval $mc create line [expr $x+$w+20] [expr $y+$h/2] [expr $x+$w+0] [expr $y+$h/2] -width 2 -fill darkblue -tags "{$name newblock pin p2 typeout $moretags}"
} default {
puts stdout "Unknown network element" $type
}
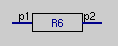
}Some elements used in Bwise:
It shouldn't be too hard to adapt the elements shape because I in the procedure newnetwelm use variables for the width and the height of the drawn element. For the moment there are three major lines in this subject I think: more elements, getting a netlist of the resulting schematics, maybe with the separate determination of the network nodes (or loops) in the equivalent electrical network, and of course we will want to generate a (possibly complex and with rational/symbolic computations) matrix which describes a physically realisable system with the Modified Nodal Analysis method (see for instance [L1 ] ) and preferably solve for the currents or voltages in the network!
For an example of the solving of a (complex) system of linear equaltions in matrix form using tcl driving maxima to do the symbolic processing, see interfacing tcl to solve matrices in maxima.
First an improved item drawing which allows us to rotate the network elements, and lets us desig new elements a bit easier and more transparent, I added these procedures:
proc rot2dx {x y a} {
return [ expr cos($a) *$x - sin($a) *$y ]
}
proc rot2dy {x y a} {
return [ expr sin($a) *$x + cos($a) *$y ]
}
proc itemaffine {{l {0 0 10 10}} {x 0} {y 0} {a 0}} {
set r {}
set phi [expr 2*3.141592653589793*$a/360]
foreach {xi yi} $l {
append r " [expr $x+[rot2dx $xi $yi $phi]] [expr $y+[rot2dy $xi $yi $phi]]"
}
return $r
}to rotate a point in 2D coordinate space, like in Vector rotations with Bwise and perform an affine transformation (minus scaling thus far) on canvas coordinates. Using these, the new network element creation proc becomes:
proc newnetwelm { {name {}} {x {0}} {y {0}} {type {R}} {phi {90}} {moretags {}} } {
global bcount mw mc
switch $type R {
set w 50 ; set h 18 ; set pinsin p1 ; set pinsout p2
if {$name == ""} {set name "R$bcount" ; set bcount [expr $bcount +1]}
$mc create poly [itemaffine "0 0 $w 0 $w $h 0 $h" $x $y $phi] -tags [list $name newblock block $moretags] -fill {} -outline black
$mc create text [itemaffine "[expr $w/2] [expr $h/2+1]" $x $y $phi ] -anchor c -text $name -fill darkblue -tags [list $name crb label $moretags]
set ii 0
foreach i $pinsin {
eval $mc create text [ itemaffine [list [expr -1] [expr 9+$ii]] $x $y $phi ] -anchor se -text $i -tags "{$name crb pinname $i $moretags}"
eval $mc create line [ itemaffine [list [expr -20] [expr 10+$ii] [expr 0] [expr 10+$ii]] $x $y $phi ] -width 2 -fill darkblue -tags "{$name newblock pin $i typein $moretags}"
set ii [expr $ii+15]
}
set ii 0
foreach i $pinsout {
eval $mc create text [ itemaffine [list [expr $w+9] [expr 19+$ii]] $x $y $phi ] -anchor c -text $i -tags "{$name crb pinname $i $moretags}"
eval $mc create line [ itemaffine [list [expr $w+20] [expr 10+$ii] [expr $w+0] [expr 10+$ii]] $x $y $phi] -width 2 -fill darkblue -tags "{$name newblock pin $i typeout $moretags}"
set ii [expr $ii+15]
}
} C {
set w 18 ; set h 27
if {$name == ""} {set name "C$bcount" ; set bcount [expr $bcount +1]}
eval $mc create poly [itemaffine [list 0 0 [expr $w/3] 0 [expr $w/3] $h 0 $h] $x $y $phi] -tags "{$name newblock block $moretags}" -fill black -outline black
eval $mc create poly [itemaffine [list [expr 2*$w/3] 0 $w 0 $w $h [expr 2*$w/3] $h] $x $y $phi] -tags "{$name newblock block $moretags}" -fill black -outline black
eval $mc create text [itemaffine [list [expr $w/2] [expr $h+10]] $x $y $phi] -anchor c -text $name -fill darkblue -tags "{$name crb label $moretags}"
eval $mc create text [ itemaffine [list -1 9] $x $y $phi ] -anchor se -text p1 -tags "{$name crb pinname p1 $moretags}"
eval $mc create line [ itemaffine [list -20 10 0 10] $x $y $phi ] -width 2 -fill darkblue -tags "{$name newblock pin p1 typein $moretags}"
eval $mc create text [ itemaffine [list [expr $w+9] 19] $x $y $phi ] -anchor c -text p2 -tags "{$name crb pinname p2 $moretags}"
eval $mc create line [ itemaffine [list [expr $w+20] 10 $w 10] $x $y $phi ] -width 2 -fill darkblue -tags "{$name newblock pin p2 typeout $moretags}"
} V {
set w 25 ; set h 25
$mc create oval [itemaffine "0 0 $w $h" $x $y $phi] -tags [list $name newblock block $moretags] -fill {} -outline black
$mc create line [itemaffine "[expr 3*$w/8] [expr -$h/4] [expr 3*$w/8] [expr -2*$h/4]" $x $y $phi] -tags [list $name newblock block $moretags] -fill black
$mc create line [itemaffine "[expr 2*$w/8] [expr -3*$h/8] [expr 4*$w/8] [expr -3*$h/8]" $x $y $phi] -tags [list $name newblock block $moretags] -fill black
eval $mc create text [itemaffine [list [expr $w/2] [expr $h+10]] $x $y $phi] -anchor c -text $name -fill darkblue -tags "{$name crb label $moretags}"
eval $mc create text [ itemaffine [list -1 9] $x $y $phi ] -anchor se -text p1 -tags "{$name crb pinname p1 $moretags}"
eval $mc create line [ itemaffine [list -20 10 0 10] $x $y $phi ] -width 2 -fill darkblue -tags "{$name newblock pin p1 typein $moretags}"
eval $mc create text [ itemaffine [list [expr $w+9] 19] $x $y $phi ] -anchor c -text p2 -tags "{$name crb pinname p2 $moretags}"
eval $mc create line [ itemaffine [list [expr $w+20] 10 $w 10] $x $y $phi ] -width 2 -fill darkblue -tags "{$name newblock pin p2 typeout $moretags}"
} I {
set w 25 ; set h 25
$mc create oval [itemaffine "0 0 $w $h" $x $y $phi] -tags [list $name newblock block $moretags] -fill {} -outline black
$mc create line [itemaffine "[expr $w/2] 0 [expr $w/2] $h" $x $y $phi] -tags [list $name newblock block $moretags] -fill black
$mc create line [itemaffine "[expr 3*$w/8] [expr -$h/4] [expr 3*$w/8] [expr -2*$h/4]" $x $y $phi] -tags [list $name newblock block $moretags] -fill black
$mc create line [itemaffine "[expr 2*$w/8] [expr -3*$h/8] [expr 4*$w/8] [expr -3*$h/8]" $x $y $phi] -tags [list $name newblock block $moretags] -fill black
eval $mc create text [itemaffine [list [expr $w/2] [expr $h+10]] $x $y $phi] -anchor c -text $name -fill darkblue -tags "{$name crb label $moretags}"
eval $mc create text [ itemaffine [list -1 9] $x $y $phi ] -anchor se -text p1 -tags "{$name crb pinname p1 $moretags}"
eval $mc create line [ itemaffine [list -20 10 0 10] $x $y $phi ] -width 2 -fill darkblue -tags "{$name newblock pin p1 typein $moretags}"
eval $mc create text [ itemaffine [list [expr $w+9] 19] $x $y $phi ] -anchor c -text p2 -tags "{$name crb pinname p2 $moretags}"
eval $mc create line [ itemaffine [list [expr $w+20] 10 $w 10] $x $y $phi ] -width 2 -fill darkblue -tags "{$name newblock pin p2 typeout $moretags}"
} default {
puts stdout "Unknown network element" $type
}
}We can now add a rotation to the argument list to make resistors (I'll update the C part, too --done--) under an angle:
To get an drawing of all thus defined elements (anyone want to do a coil or opamp ?) :
newnetwelm V1 650 160 V 90 newnetwelm C2 50 160 C 90 newnetwelm V2 550 160 V 0 newnetwelm I1 850 160 I 90 newnetwelm I2 750 160 V 0 $mc del I2 newnetwelm I2 750 160 I 0 newnetwelm R1 150 160 R 90 newnetwelm C1 250 160 C 0 newnetwelm R2 350 160 R 0
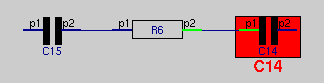
Probably it is a reasonable idea to use the bwise function otherpins to find out all the connected network elements to one network 'Node' which isn't exactly the same as the normal bwise connection meaning, for instance having loaded or created the above network (note that the functions starting with new are listed in the right mouse button bwise menu automatically):
% otherpins R223 p2
{R224 p1} {R19 p1} {R28 p2}This command output corresponds with this example resistornetwork [L2 ]
As a weekend fun idea: suppose we have N resistors, labelled R1...Rn, how many (and which!) networks can be made with them, and what are the varying replacement values of the networks which are seen as twopoles when it is given that R1 <= Ri <= Ri+1 <= Rn ....
To compute the currents and the voltages in a newtork, we probably want matrix computations for which I use Maxima, lets do an example. To run maxima (which needs to be installed, and I use Linux in this example, see Bwise blocks using exec maxima) I use two main functions in this case:
proc domaxima { {m} } {
set t "display2d:false;\n$m;"
return [string range [exec maxima -q << $t ] 32 end-7]
}
proc domaxima2d { {m} } {
set t "display2d:true;\n$m;"
return [string range [exec maxima -q << $t ] 56 end-7]
}now we can either pretty-printed or reusable algebra-like work with maxima and its matrix computations (very large numbers, symbolic computations, etc.), for instance:
(Tcl) % domaxima2d { matrix(
[s*c1+s*c2+1/(s*l1)+1/(r1),-s*c2,0,0],
[-s*c2,s*c2+1/r2,-1/r2,0],
[0,-1/r2,1/r2,1],
[0,0,1,0]
)}
[ 1 1 ]
[ c2 s + c1 s + ---- + -- - c2 s 0 0 ]
[ l1 s r1 ]
[ ]
[ 1 1 ]
[ - c2 s c2 s + -- - -- 0 ]
(%o2) [ r2 r2 ]
[ ]
[ 1 1 ]
[ 0 - -- -- 1 ]
[ r2 r2 ]
[ ]
[ 0 0 1 0 ]
Which in fact is the network equation matrix from an example from [L3 ], which in this manner we can work on. This matrix can be derived for every existable electrical network composed of linear and linear reactive elements, and can even for most cases (maybe all, I don't recall, but every normal electronic filter without shorts lets say) be proven to be invertible using always functioning schemes like "sweeping" (Gaussian elimination), so that no iterative solver (and thus inaccuracies and convergence issues) is needed. This is possibly after a row-exchange step which can be modeled as the almost simplest of orthogonal transforms: the permutation matrix.
Why all this here? Well, the whole scheme can be made to operate on infinite number accuracy present maxima(using tcl), and the matrix inversion is possible for all relevant networks without iteration, and acting also on formula-based elements (so not having to approximate PI and so on) making parametric designs trivial. The formulas of the elements can be made andused in tcl as lists, and coupled with BWise. I'm sure there are good third year EE uni students who could do this, it's a good exercise. Inform me or put it here if you do! The scripting and Tk additions make the whole then flexible.
See also: a small operating-point circuit simulator