Decision trees

WikiDbImage dtree.gif

Richard Suchenwirth 2002-06-22 - Decision trees are, in this simple model, binary trees which are walked from the root node by asking the yes-no question associated to a node, and branching according to the answer, until a terminal node is reached, which is the solution.

Imagine a game where a number between 1 and 9 is to be guessed. A possible decision tree (in nested list notation, where each non-terminal node has three elements: the question, and the decision trees for the "no (0) and "yes" (1) case) could be this: }

 set guess19 {
    even {
        prime {
            "multiple of 3" 1 9
        } {
            "multiple of 3" {
                "divisor of 10" 7 5
            } 3
        } 
    } {
        prime {
            square {
                "multiple of 3" 8 6
            } 4
        } 2
    }
 }

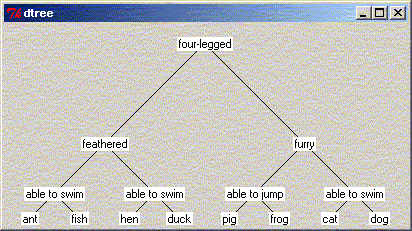
if 0 {Another example, an animal-guessing game:}

 set animals {
    four-legged {
        feathered {
            "able to swim" ant fish
        } {
            "able to swim" hen duck
        }
    } {
        furry {
            "able to jump" pig frog
        } {
            "able to swim" cat dog
        }
    }
 }

if 0 {For walking a decision tree from root to solution we write a generic recursive function that takes a tree and the names of two functions for asking resp. answering, so it can be used both in stdio-based tclsh and a Tk UI:}

 proc walkDtree {dt askF answerF} {
    switch -- [llength $dt] {
        1 {$answerF $dt}
        3 {
            if [$askF [lindex $dt 0]] {
                walkDtree [lindex $dt 2] $askF $answerF
            } else {
                walkDtree [lindex $dt 1] $askF $answerF
            }
          }
        default {error "bad dtree $dt, must have 1 or 3 elements"}
    }
 }

# Now testing, first in stdin/stdout (SIO) mode:

 proc walkDtreeSIO dt {
     while 1 {
        # easily terminated by entering a non-Boolean answer
        puts "Guess one of [lsort [dtreeLeaves $dt]]."
        walkDtree $dt askSIO answerSIO
     }
 }
 proc askSIO question {
    puts -nonewline "Is it $question? "
    flush stdout
    gets stdin answer
    expr {$answer && 1} ;# force boolean evaluation
 }
 proc answerSIO answer {
    puts "The answer is $answer."
 }
 proc dtreeLeaves dt {
    switch -- [llength $dt] {
        1 {set dt}
        3 {
            concat [dtreeLeaves [lindex $dt 1]] \
                   [dtreeLeaves [lindex $dt 2]]
          }
        default {error "bad dtree $dt, must have 1 or 3 elements"}
    }    
 }

# ... and a Tk version, which includes a tree display:

 proc walkDtreeUI dt {
    text .t -width 50 -wrap word
    frame .f
    button .f.1 -text Yes -command {set ::answer yes}
    button .f.0 -text No  -command {set ::answer no}
    button .f.c -text ? -command [list toplevelDtree $dt]
    pack .f.1 .f.0 .f.c -side left -fill x -expand 1
    pack .t .f -fill x
    bind . <Escape> {exec wish $argv0 &; exit}
    while 1 {
        .t insert end "Guess one of: [lsort [dtreeLeaves $dt]]:\n"
        walkDtree $dt askUI answerUI
    }
 }
 proc askUI question {
    .t insert end "Is it $question? "
    .t see end
    vwait ::answer
    .t insert end $::answer\n
    expr {$::answer=="yes"}
 }
 proc answerUI answer {
    .t insert end "The answer is $answer.\n\n"
    .t see end
 }

#-------------------------------- Decision tree visualization:

 proc dtree2canvas {dt c x y {xm 0} }  {
    set id [$c create text $x $y -text [lindex $dt 0] -tag txt]
    switch -- [llength $dt] {
        1 {# nothing more to do for a leaf}
        3 {
            set offset [expr {abs($x-$xm)/2}]
            set x0 [expr {$x - $offset}]
            set x1 [expr {$x + $offset}]
            set y1 [expr {$y + $offset}]
            $c create line $x $y $x0 $y1
            dtree2canvas [lindex $dt 1] $c $x0 $y1 $x
            $c create line $x $y $x1 $y1
            dtree2canvas [lindex $dt 2] $c $x1 $y1 $x
          }
        default {error "bad dtree $dt, must have 1 or 3 elements"}
    }    
    $c create rect [$c bbox $id] -fill white -outline white
    $c raise txt
 }
 proc toplevelDtree dt {
    if {![winfo exists .dtree]} {
        toplevel .dtree
        pack [canvas .dtree.c -width 400 -height 200]
        dtree2canvas $dt .dtree.c 200 20
    }
    raise .dtree
 }
 if {[package provide Tk]!=""} {walkDtreeUI $animals}

if 0 {This works the way it should. After some tries you of course notice that the sequence of questions is predictable - it should, because we constructed it into the decision tree. But it would be nicer if we didn't have to construct such a tree structure ourselves, but let Tcl do it - starting from a set of stated facts, where each fact is a predicate and the list of cases for which it holds:}

 set facts19 {
    {even {2 4 6 8}}
    {prime {2 3 5 7}}
    {square {1 4 9}}
    {"multiple of 3" {3 6 9}}
    {"divisor of 10" {1 2 5}}
 }

if 0 {In order to traverse the tree with as few as possible questions, it should be balanced, so that the weight difference between left and right branch is minimal. Therefore we determine the "best fact":}

 proc facts2dtree {facts {choices {}} } {
    if {$choices==""} {set choices [facts2choices $facts]}
    if {[llength $choices]==1} {return $choices}
    foreach {name bchoices} [bestFact $facts $choices] break
    list $name \
         [facts2dtree $facts [allbut $choices $bchoices]]\
         [facts2dtree $facts $bchoices]
 }
 proc facts2choices facts {
    # determine the "universe" from a set of facts
    set res {}
    foreach fact $facts {
        foreach i [lindex $fact 1] {
            if {[lsearch $res $i]<0} {lappend res $i}
        }
    }
    set res
 }
 proc bestFact {facts choices} {
    set nchoices [llength $choices]
    set center [expr {$nchoices / 2.}] ;# optimum balance
    set t {}
    foreach fact $facts {
        foreach {name cases} $fact break
        set validcases [intersect $cases $choices]
        set nvalid [llength $validcases]
        if {$nvalid>0 && $nvalid<$nchoices} {
            lappend t [list \
                [expr {abs([llength $validcases]-$center)}]\
                $name $validcases]
        }
    }
    if {[llength $t] == 0} {
        error "no way to distinguish $choices - add more facts"
    }
    foreach {- name c} [lindex [lsort -index 0 -real $t] 0] break
    list $name [intersect $choices $c]
 }
 #-------------------------------- general set handling routines
 proc allbut {all but} {
    # returns all elements of 'all' that are not in 'but'
    set res {}
    foreach i $all {
        if {[lsearch $but $i]<0} {lappend res $i}
    }
    set res
 }
 proc intersect {list1 list2} {
    # returns all elements that are both in list1 and list2
    set res {}
    foreach i $list1 {
        if {[lsearch $list2 $i]>=0} {lappend res $i}
    }
    set res
 }

After this purely home-grown toy, a bigger one based on the C4.5 system is at Playing C4.5

EMJ - Well, since this is starting to look like Animal [L1 ], does anyone want to make it learn new facts? (No, don't even think about the Pervade bit!)

NEM - Your wish is my command: a little learning decision tree.

Alex Caldwell - Could the dtree2canvas and WalkDtreeUI be modified to handle trees that are not strictly binary trees? In medical decision support flow trees, there are often more than two choices for a question. The flow charts are very similar, but they may have 3 or more choices at each level in the tree, each with more children. If I could display a tree like that in a canvas the way this does with the binary tree, and have it auto calculate it's layout, I would be most grateful. Maybe we could even make some money with it by supplying a decision support system that would link into physcian's EMRs (electronic medical records).

AK: Looked over the code and see nothing against that in principle. The tricky point will be to compute good offsets for the subtrees. Oner thing Richard skipped over in this demo was to account for the string-length. That allowed him to use a simple top-down algorithm. For proper layout we need a bottom-up phase to collect size info, followed by top-down to arrange the sub-trees according to the sizes. Even so, definitely possible.

Alex Caldwell - I have something working for this with non-binary trees in the BWidget tree based on Trees as nested lists that works pretty well. But I like the appearance and style of the layout on this page better. I think most physicians are used to looking a flow chart in their magazines that looks like this, rather than the directory tree style of the BWidget tree example. I have another demo I made a few years ago of what I'm trying to do in a Starpack at [L2 ]. It's a binary tree based on a Tcl nested list that uses some code off this page to display it in a Tk canvas. But it also uses the Canvas Buttons extension to allow non-discreet, or continuous type data choices before a binary decision threshold is triggered. Because of the sometimes long text strings, I made the layout left to right, but it is still impossible to see the whole tree on one screen, only a small window onto it. It actually works, but producing the nested list for it was a major headache that I did by hand. With Playing C4.5 and a little learning decision tree I can envision being able to create the nested lists automatically now, based on some real patient data combined with input by some non-programming medical experts, and then turn it into a useful interactive flow chart.