Dial widget
From a news:comp.lang.tcl posting by Roger E Critchlow on Aug 17, 1999 --
Create a window, $w, with an analog dial of $diameter pixels, background color $bg, foreground color $fg, and middleground color $mg. The dial will update the frequency stored in the global named $var between minimum value $min and maximum value $max. Grab the dial anywhere with the left mouse button and spin, the marker that spins is only there to give you some rotational feedback. The concentric regions marked on the dial give different update speeds depending on which region you grab with the mouse. The mouse is tracked anywhere on the screen as long as the button remains depressed, so you can get nice fine adjustments by pulling the mouse way outside the dial.
proc dial {w var min max diameter bg fg mg} { # create the dial canvas canvas $w -width $diameter -height $diameter -bg $bg \ -highlightthickness 0 # create a data array upvar \#0 $w data # cleanup the data array bind $w <Destroy> [list unset $w] # save arguments foreach v {w var min max diameter bg fg mg} { set data($v) [set $v] } # compute some values set data(x0) [expr {$diameter/2}] set data(y0) [expr {$diameter/2}] set data(r0) [expr {($diameter-10)/2}] set data(dr) [expr {$data(r0)/5}] set data(mark-theta) 250 set data(2pi) [expr {2*atan2(0,-1)}] # create the dial disk $w create oval 5 5 [expr {$diameter-5}] [expr {$diameter-5}] \ -fill $fg -outline $mg -width 4 \ -tags dial # mark the resolution radii with concentric circles foreach d {2 3 4} { set r [expr {$d*$data(dr)}] $w create oval \ [expr {$data(x0)-$r}] [expr {$data(y0)-$r}] \ [expr {$data(x0)+$r}] [expr {$data(y0)+$r}] \ -fill {} -outline $mg -width 4 \ -tags dial } # draw a rotating marker $w create line $data(x0) $data(y0) $data(x0) 5 \ -width 4 -fill $mg -arrow last \ -tags {dial mark} # press binding $w bind dial <ButtonPress-1> {dial-press %W %x %y} # motion binding $w bind dial <B1-Motion> {dial-motion %W %x %y} # return our window return $w } proc dial-press {w x y} { # bind to data array upvar \#0 $w data # determine radius and theta set x [expr {$x-$data(x0)}] set y [expr {$data(y0)-$y}] set data(r) [expr {sqrt($x*$x+$y*$y)}] set data(theta) [expr {int(1000*atan2($y,$x)/$data(2pi))}] # compute frequency update for this radius # this assumes the 1000 counts/rev done below switch [expr {int(($data(r0)-$data(r))/$data(dr))}] { 0 { set data(kHz/count) 0.01; # 10 kHz/rev } 1 { set data(kHz/count) 0.1; # 100 kHz/rev } 2 { set data(kHz/count) 1; # 1 MHz/rev } default { set data(kHz/count) 10; # 10 MHz/rev } } } proc dial-motion {w x y} { # bind to data array upvar \#0 $w data # compute dtheta set x [expr {$x-$data(x0)}] set y [expr {$data(y0)-$y}] set dtheta [expr {(int(1000*atan2($y,$x)/$data(2pi))-$data(theta))%1000}] if {$dtheta > 500} { set dtheta [expr {$dtheta-1000}] } # update theta set data(theta) [expr {($data(theta)+$dtheta)%1000}] # update marker set data(mark-theta) [expr {$data(mark-theta)+$dtheta}] set t [expr {$data(2pi)*$data(mark-theta)/1000}] $w coords mark $data(x0) $data(y0) \ [expr {$data(r0)*cos($t)+$data(x0)}] \ [expr {$data(y0)-$data(r0)*sin($t)}] # update frequency upvar \#0 $data(var) frequency set f [expr {$frequency-$dtheta*$data(kHz/count)}] if {$f < $data(min)} { set f $data(min) } elseif {$f > $data(max)} { set f $data(max) } # update frequency variable set frequency [format %12.2f $f] } # Here's some demo code: set bg \#4f4f4f set fg grey set mg white set frequency 15000.00 . configure -bg $bg pack [frame .f -bg $bg] -side top -fill x pack [label .f.l -font {-size 32} -width 9 -anchor e \ -textvar frequency -bg $bg -fg $mg] -side left pack [label .f.hz -font {-size 32} -text "kHz" -bg $bg -fg $mg] -side left pack [dial .d frequency 0.00 30000.0 200 $bg $fg $mg] -side top
uniquename 2014jan27
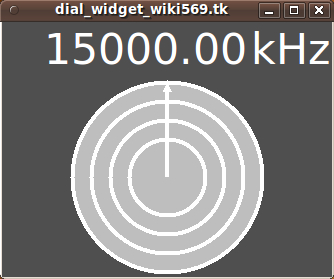
For those who do not have the facilities or time to implement the code above, here is an image of the dial and needle that are drawn on a Tk 'canvas' --- which is packed below a 'frame' widget containing a couple of 'label' widgets.
You can drag the needle either clockwise or counter-clockwise --- and the displayed number either increases or decreases, respectively.
This dial-and-needle could be 'hooked up' to a function that animates the dial according to a time variable. The Tcl 'after $millisecs' command could be used to advance the time variable at a suitable rate --- in particular, to keep the process of needle-updating from proceeding so fast that it uses CPU-cycles at a ridiculous, CPU-temperature-elevating rate.