Estimating Mountain Height Using Look Angles, Etcl Console Example
Estimating Mountain Height Using Look Angles, Etcl Console Example
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER in your comment with the same courtesy that I will give you. Its very hard to reply intelligibly without some background of the correspondent. Thanks,gold
- Estimating Mountain Height Using Look Angles, Etcl Console Example
- Introduction
- Testcase
- Comments Section
Introduction
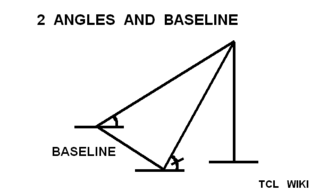
gold Here is an eTCL script on estimating mountain height for the etcl console. I found an angle(s) and baseline formula in a precalculus book. The formula for mountain height was baseline*sin(aa)*sin(bb)/ sqrt( sin(aa)* sin(aa)-sin(bb)*sin(bb) ) The angles used are angles of elevation from the ends of the baseline. It stipulated that the baseline starting from point aa is perpendicular to the line of sight. The formula was not corrected for curvature of earth, which would be $correction = earth_radius * (secant (arclength/earth_radius))-earth_radius. arclength is the arclength from the observer to the mountain.
In planning any software, there is a need to develop testcases. With back of envelope calculations, we can develop a number of peg points to check output of program.
Testcase
| quantity | angle | units | angle | units | baseline | answer | method |
|---|---|---|---|---|---|---|---|
| 1.0 | 30 | degrees | 20 | degrees | 10 | 4.69 | textbook |
Screenshots Section
figure 1.
References:
- http://www.grc.nasa.gov/WWW/K-12/airplane/kitedrv.html
- Oneliner's Pie in the Sky
- Swokowski and Cole's Algebra and Trigonometry with Analytic Geometry,page 392.
Appendix TCL programs and scripts
Pretty Print Version
# Pretty print version from autoindent
# and ased editor
# written on Windows XP on eTCL
# code from TCL WIKI, eTCL console script
# 8jun2011, [gold]
console show
proc deg2rad {} {return [ expr {1.*[pi]/180.} ]}
proc rad2deg {} {return [ expr {180./[pi]} ]}
proc pi {} {expr 1.*acos(-1)}
set counter 1
proc mountain { angle1 angle2 baseline } {
global counter past
set angle1 [ expr { [deg2rad]*$angle1*1. } ]
set angle2 [ expr { [deg2rad]*$angle2*1. } ]
set nom [ expr { $baseline*sin($angle1)*sin($angle2)*1. } ]
set denom [ expr { sin($angle1)*sin($angle1) -sin($angle2)*sin($angle2) } ]
set denom [ expr { abs($denom)*1. } ]
set denom [ expr { sqrt($denom)*1. } ]
set xheight [ expr {1.* $nom/$denom } ]
puts "$counter $angle1 $angle2 distance $baseline moun $xheight "
incr counter
wm title . "estimating mountain height"
}
mountain 30 20 10Notes & Code scraps
Another baseline formula was used by Al Biruni as height= (baseline*tan(angle1)*tan(angle2))/ (tan(angle2)-tan(angle1))
Comments Section
Please place any comments here, Thanks.
Why do you utilize meaningless variable names in many of your procedures? I.e., aa, bb, cc as the inputs to mountain. Absent external explanations, aa, bb , cc have no meaning and therefore the names themselves do not help to guide a reader as to their meaning. Additionally, nom, denom have some meaning, numerator, denominator, but that meaning is self evident by being utilized in a division operation, so in the end, those names also convey zero additional meaning. Your example would be far easier to understand if you picked variable names that related to the real-world values that aa, bb, cc, nom, and denom actually represented.
gold2Dec2018. Continuing. I found this trig formula in a two sentence problem from a very old textbook. The trig formula was not derived at all. Perhaps all known trig quantities were not recognized and named as special quantities in the real world, for me.
gold 2Dec2018. Important Note. See better routines and current methods for angle reduction, sin, cos, etc in the TCL core distribution and TCLLIB. As of Jul2018, the TCLLIB has developed code for trig angles in degrees, trig inverse, and hyper functions in degrees, and angle reduction in radians and degrees. This supplemental trig.tcl, trigtest.tcl, and trig.man code is posted on the TCLLIB website.z This math::trig.tcl seems really exciting work, which will keep TCL in pace with some of the other brand name languages (math oriented, I mean).
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |