Gaussian Distribution

started by Theo Verelst

The gaussian distribution is also called Normal Distribution. For most physical independent measurements it holds that the statistical law of large numbers makes a measurement distribution graph due to measurement noise [ CL observes that, strictly speaking, the noise doesn't have to be due to measurement, but it must be additive. This turns out to be a reasonable assumption for a wide range of circumstances ] [ RFox Strictly speaking a Normal Distribution integrates to one. As my daddy the statistician observed when I grew up, often 'gaussian functions' are mis-called Gaussian Distributions and are not actually distributions at all-- unless they integrate to 1 -- us physicists are very fond of interchanging Gaussian Distribution/Function when talking about peak shapes in data ] is a normal or Gaussian distributed probability density.

Often, you will need to test some data for normality (see testing for normality) before you can apply some sort of statistical tests.

So if we flip a coin so many times, and keep score of 10 throws for instance, we expect to get an average of 5 heads for ten throws. But of course, it will also happen we throw 6 heads or even 7 tails. And if we wait long enough, a sequence of 8 head is not out of the question, as we all know, the probability of throwing 10 tails on a row is even reasonably possible, but chances are 1/2^10=1024, so in a thousand experiments of 10 flips, that starts to become reasonably likely. (How likely !? :)

This little script computes 100,000 times the average of 5 random numbers (from the rand() tcl function), and stores the normalized results in a list called to:

catch {unset to};  for {set j 0} {$j < 100000} {incr j} {
    set o 0; set u 5
    for {set i 0} {$i < $u} {incr i} {
       set o [expr {$o+rand()}]
    }
    lappend to [expr {$o/$u}]
}

Now we'll make 300 buckets in which we count how much of the result fits between to adjacent bucket limits:

catch {unset gd}
for {set i 0} {$i<300} {incr i} {set gd($i) 0}
foreach i $to {incr gd([expr {int([expr $i*300])}])}

And display the result as a reasonably accurate bar graph on the bwise canvas, or you should have a visible Tk canvas of which the path is in the variable mc :

mc del gr3
foreach n [array names gd] {
    $mc create line [expr {100+$n}] 301 [expr {100+$n}] [
        expr {300-0.2*$gd($n)}] -tag gr3}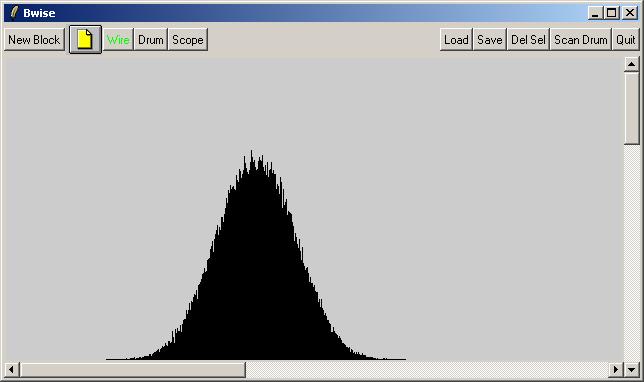

Image TV Wiki gaussian1.jpg

At least clearly the gaussian curve can be recognized, where the statistical measure 'variance' can be derived from the bowing points (the change of sign of the second derivative, at both sides of the maximum, the expectation value). Also clearly, a hundred thousand samples still leave us with considerable deviation from the ideal 'big numbers' curve.

Normally, for natural random processes, the law of big numbers works pretty well.

TR: here is another way of generating random numbers from a normal distribution. It also uses the central limit theorem (law of big numbers):

proc RandomNormal {mean sd} {
    #
    # generate a random number that is normally distibuted
    # using the central limit theorem
    #
    # mean -> expected mean of the generated numbers
    # sd -> expected standard deviation of the generated numbers
    #
    
    # number of iterations (the higher, the better, the slower):
    set n 150
    # produce n equally random integers from [0,1]
    set sum 0
    for {set i 0} {$i < $n} {incr i} {
        set sum [expr {$sum + int(rand()*2)}]
    }
    # transform the sum to the interval [0,1] again -> sum/n
    # and then transform to [mean,sd^2]
    #
    return [expr {((($sum/double($n))-0.5) * sqrt($n*12)) * $sd + $mean}]
}

KBK 2004-03-31:

One conventional way to sample a random variable from a Gaussian distribution is Marsaglia's polar method (another description ). This method is usually faster than any method that involves the Central Limit Theorem and a large batch of random numbers. It also has precision that is limited only by the precision of the underlying random number generator.

The following Tcl code samples 50000 numbers from the normal distribution and displays a histogram of the samples, together with the Gaussian "bell-shaped curve". The "nordev" procedure should be generally useful wherever a Gaussian random variable is needed.

# Procedure that returns a random variable sampled from a Gaussian
# distribution with mean zero and standard deviation unity.

proc nordev {} {
    variable last
    if { [info exists last] } {
        set retval $last
        unset last
        return $retval
    }
    set v1 [expr { 2. * rand() - 1 }]
    set v2 [expr { 2. * rand() - 1 }]
    set rsq [expr { $v1*$v1 + $v2*$v2 }]
    while { $rsq > 1. } {
        set v1 [expr { 2. * rand() - 1 }]
        set v2 [expr { 2. * rand() - 1 }]
        set rsq [expr { $v1*$v1 + $v2*$v2 }]
    }
    set fac [expr { sqrt( -2. * log( $rsq ) / $rsq ) }]
    set last [expr { $v1 * $fac }]
    return [expr { $v2 * $fac }]
}

 Calculate 50000 normal deviates, and prepare a histogram of them.

set l { 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 }
for { set i 0 } { $i < 50000 } { incr i } {
    set d [nordev]
    set bin [expr {int(20 + floor( 4. * $d))}]
    lset l $bin [expr {[lindex $l $bin] + 1}]
}

 Display the histogram on a Tk canvas, together with the
 Gaussian error function

package require Tk
grid [canvas .c -width 400 -height 200 -bg white]
set max 0
foreach v $l {
    if { $v > $max } {
        set max $v
    }
}
set x 0
set coords {}
foreach v $l {
    set y [expr {190-(180*$v/$max)}]
    set x2 [expr {$x+10}]
    .c create rectangle $x $y $x2 190 -outline black -fill {}
    set x $x2
}
set c {}
for { set i 0 } { $i <= 400 } { incr i } {
    set sigma [expr { 0.025 * ( $i - 200 ) }]
    set y [expr { 190. - 180. * exp( -$sigma*$sigma / 2 ) }]
    lappend c $i $y
}
.c create line 0 190 400 190 -fill red
.c create line 200 0 200 200 -fill red
eval [list .c create line] $c [list -fill blue]

TV: Ouch, an if in the devnor proc in the random data datapath, and sqrt's and such, well well. I just wanted to analyze the rand() data straightforward, as in a dice purity test or something.

The above seems to give cleaner result, though I find the asymmetry of the stripes troubling, but so does the direct analysis with similar number of rnd experiments (even less) and largely decreased bucket size.

And frankly, I wouldn't know what not to trust when this latter code gives wrong distributions in the end: the rand() or the math involved in creating a normal distribution. The above example simply adds and averages, nothing special, it should converge neatly to ND, why it doesn't all too nicely makes me suspect rand()...

Anyhow, it's interesting material, and I know from theoretical physics (though it's been a while) that one can get very far with only relatively simple statistically based reasoning. IF one calls conditional probabilities (densities), as taught in highschool, simple after a while...

On this page at about 80% pictures of the gaussian combined with sine and cosine, a *very* important concept.

CL finds it easy to get misty-eyed about the ubiquity of the gaussian in important contexts. It's only a step away from discussions of Heisenberg's principle, Shannon optimization, market-pricing theories, Einstein's brilliant work on brownian motion and atomism, fourier transforms, ...

Gaussian Distribution

See Also