Parrondo's Paradox
Arjen Markus (4 january 2015) Parrondo's Paradox, described in some detail in this Wikipedia page and clearly analysed in this article illustrates how statistics can be highly unintuitive. The paradox is shown here via two simple games:
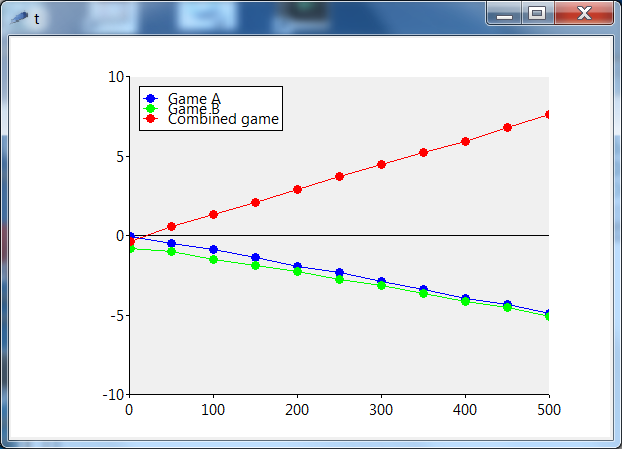
- In game A a single unfair coin is tossed: there is a probability of 49.5% that it is "heads". This increases your capital by 1, whereas "tails" means you lose 1. Clearly, in the long run you will have a negative capital.
- In game B two coins are tossed. If your current capital is divisible by three, coin 1 is used, otherwise coin 2 is tossed. Again "heads" increases your capital by 1 and "tails" decreases it by the same amount. Coin 1 gives "heads" with a 9.5% probability and coin 2 gives "heads" in 74.5% of the tosses - but it is used less. Again the expected outcome in the long run is negative.
Now we combine the two games: we throw an unbiased coin to select game A or game B, so 50% percent of the time we play game A and 50% percent of the time we play game B.
The surprising thing is, that this combined game is a winning game:
I have implemented this using the vectcl package, as playing a large number of these games in parallel is required to estimate the mean outcome. Here is the code, it is only one possibility of course. Note the way Plotchart is integrated with the calculation.
# parrondo.tcl --
# Simulation of Parrondo's Paradox: two losing games combined give a winning game.
#
# The simulation concerns 10000 instances of the separate games and the
# combined game over 500 steps.
#
# Note: not really optimised yet
#
package require vectcl
lappend auto_path c:/tcl/lib
package require Plotchart
# fillzero --
# Return an array of integer zeros (constfill returns doubles)
#
# Arguments:
# sz Size of the array
#
# Returns:
# Array of "sz" integer zeros
#
proc fillzero {sz} {
lrepeat $sz 0
}
# randomNumbers --
# Return a list of random numbers
#
# Arguments:
# sz Size of the list
#
# Returns:
# Array of "sz" random numbers
#
proc randomNumbers {sz} {
lmap _ [lrepeat $sz {}] {expr rand()}
}
# gameA --
# Determine the outcome according to game A
#
# Arguments:
# capital Current capital for all the instances
#
# Returns:
# Vector of win/loss amounts corresponding to capital
#
# Side effects:
# None
#
proc gameA {capital} {
vexpr {
sz = shape(capital)
random = randomNumbers(sz)
(random <= 0.495) - (random > 0.495)
}
}
# gameB --
# Determine the outcome according to game B
#
proc gameB {capital} {
vexpr {
sz = shape(capital)
random = randomNumbers(sz)
select = (capital%3 != 0)
select .* ((random <= 0.745) - (random > 0.745)) \
+ (1-select) .* ((random <= 0.095) - (random > 0.095))
}
}
# gameAB --
# Determine the outcome according to the combination of games A and B
#
proc gameAB {capital} {
vexpr {
sz = shape(capital)
random1 = randomNumbers(sz)
random2 = randomNumbers(sz)
selectA = (random1 > 0.5)
select2 = (capital%3 != 0)
selectA .* ((random2 <= 0.495) - (random2 > 0.495)) \
+ (1-selectA) \
.* ( select2 .* ((random2 <= 0.745) - (random2 > 0.745)) \
+ (1-select2) .* ((random2 <= 0.095) - (random2 > 0.095)) )
}
}
# plot --
# Plot the current values with an appropriate colour
#
# Arguments:
# series Series identifier for colours
# x X-value
# y Y-value
#
proc plot {series x y} {
$::p plot $series $x $y
}
# main --
# Actual simulation
#
#
# Set up the plot
#
toplevel .t
pack [canvas .t.c -width 600 -height 400]
set p [::Plotchart::createXYPlot .t.c {0 500 100} {-10 10 5}]
$p dataconfig gameA -colour blue -type both
$p dataconfig gameB -colour lime -type both
$p dataconfig gameAB -colour red -type both
# Just mark the y-axis
$p plot yaxis 0 0
$p plot yaxis 500 0
$p legendconfig -position top-left
$p legend gameA "Game A"
$p legend gameB "Game B"
$p legend gameAB "Combined game"
set zeros [fillzero 10000]
foreach game {A B AB AB2} {
puts "Game $game:"
set series "game$game"
interp alias {} game {} game$game
vexpr {
capital = zeros
for i=1:500 {
capital += game(capital)
if i == 1 || i % 50 == 0 {
plot(series,i,sum(capital)/(shape(capital)+0.0))
}
}
}
puts [vexpr {sum(capital)/(shape(capital)+0.0)}]
}aspect 2015-01-06: neat demo! I factored the code a little bit, hopefully making it clearer (less Fortranish? ;-) -- AM, no, I always forget about lmap and lrepeat - very cute. Fortran has had array operations that are quite similar to the above for at least 20 years now, since the Fortran 90 standard) without impacting performance. I didn't formally measure, but the demos didn't appear to run any slower like this.
Getting a bit more radical, the last vexpr in each Game is rather unwieldy to write. Fortunately, VecTcl syntax is incredibly easy to generate from a script! I don't have a very good name for the below proc, but it's handy for exploring the parameter space of these games:
# this needs a better name. "vif" is inspired by "vexpr if", which is hardly compelling
proc vif/3 {cond then else} {
return "(($cond) .* ($then) + (1-$cond) .* ($else))"
}
proc vif/1 {cond} {
return "(($cond)*2-1)" ;# equivalent to (($cond)*1 - (1-$cond)*1)
}
proc vif {args} {tailcall vif/[llength $args] {*}$args}With this proc, gameAB can be written more readably as:
proc gameAB2 {capital} {
vexpr {
sz = shape(capital)
random1 = randomNumbers(sz)
random2 = randomNumbers(sz)
coinA = random2 <= 0.495
coinB1 = random2 <= 0.745
coinB2 = random2 <= 0.095
flip = (random1 > 0.5)
select = (capital%3 != 0)
}
vexpr [vif flip [vif coinA] [vif select [vif coinB1] [vif coinB2]]]
}Game A and B can be retrieved by cutting chunks out of the above definition.
I hesitate to rewrite the main code in this style as it detracts from the clear exposition of vectcl above, but the pattern may be useful.