Playing Simulink
Arjen Markus (24 september 2007) In a book on fuzzy control I found a schematic drawing representing a simple system modelled via Simulink, a program by MathWorks who also market Matlab.
The drawing itself rung a bell: so that is what Simulink is all about, setting up a model of a physical system, in a similar way as an electronic circuit. Components of such a model are: adders (two signals are summed), scalers (the signal is multiplied by some constant), integrators and so on.
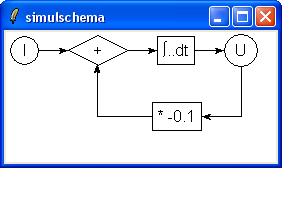
Now, that inspired me to create a simple system myself (see the scheme below):
- One input signal
- Via a feedback loop the output signal is scaled and added to the input
- The output is integrated over time
(The code to create this figure is this:
package require Diagrams namespace import ::Diagrams::* pack [canvas .c -bg white -width 270 -height 130] drawin .c circle "I" direction east arrow "" 30 set d [diamond "+"] arrow "" 30 box "\u222B..dt" arrow "" 30 circle "U" direction south line 50 -90 direction west arrow "" 40 box "* -0.1" set L [line 55 180] currentpos [getpos 0 $L] direction north arrow "" 53
using Tklib's Diagrams package. The last bit is not ideal - I had to guess at the length of 53 pixels. Dealing with such lengths should be done via a new command)
The challenge here is to make sure that the order in which the various steps are defined does not matter for the output: in a "real" system, the feedback would be almost instantaneous, so in the discrete simulation the order of the computations should not be important.
This is achieved in the script below by storing all the intermediate results in separate variables and updating the state at the end of each loop. The integration is done via a simple Euler method - more sophisticated methods would require multiple intermediate states, so, lazy as I am, I have left that as exercise.
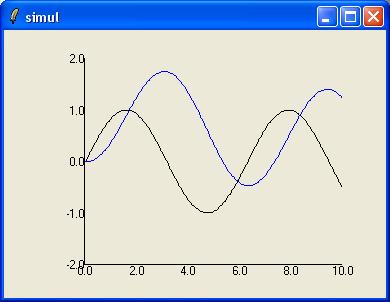
To make the script more lively, I have added a simple display (see below)
# simul.tcl --
# Simulating some aspects of Simulink
#
# The example implements the differential equation:
#
# y' = f(x) + a * y (a < 0, for stability)
#
#
# input --
# Define a time-dependent input function (does not depend on any
# state variable
#
# Arguments:
# name Name of the function
# func Expression with t as the time
#
# Result:
# None
#
# Side effects:
# Adds the definition to global variables
#
proc input {name func} {
lappend ::model [list Input $name $func]
lappend ::update "set $name \[expr $func\]" ;# Use the string representation!
}
# multiply --
# Define a multiplication with a constant
#
# Arguments:
# const Value of the constant
# name Name of the quantity
# outname Name of the result
#
# Result:
# None
#
# Side effects:
# Adds the definition to global variables
#
proc multiply {const name outname} {
lappend ::model [list Multiply $const $name $outname]
lappend ::update [list PossiblySet $name 0.0]
}
# integrate --
# Define an integration step over time
#
# Arguments:
# name Name of the quantity to be integrated
# outname Name of the result
# init Initial value (defaults to zero)
#
# Result:
# None
#
# Side effects:
# Adds the definition to global variables
#
proc integrate {name outname {init 0.0}} {
lappend ::model [list Integrate $name $outname]
lappend ::update [list PossiblySet $name 0.0]
lappend ::update [list set $outname $init] ;# Always set to the initial condition!
}
# output --
# Define an output facility
#
# Arguments:
# name Name of the quantity to be output
#
# Result:
# None
#
# Side effects:
# Adds the definition to global variables
#
proc output {name} {
lappend ::model [list Output $name]
lappend ::title $name
}
# add --
# Define an addition of two quantities
#
# Arguments:
# oper1 Name of first operand (or value)
# oper2 Name of second operand (or value)
# outname Name of the result
#
# Result:
# None
#
# Side effects:
# Adds the definition to global variables
#
proc add {oper1 oper2 outname} {
global idx
if { ! [info exists idx] } {
set idx 0
}
if { [string is double $oper1] } {
incr idx
set ::value$idx $oper1
set oper1 "::value$idx"
}
if { [string is double $oper2] } {
incr idx
set ::value$idx $oper2
set oper2 "::value$idx"
}
lappend ::model [list Add $oper1 $oper2 $outname]
lappend ::update [list PossiblySet $oper1 0.0]
lappend ::update [list PossiblySet $oper2 0.0]
}
# PossiblySet --
# Set a variable if not already set
#
# Arguments:
# name Name of the variable
# value Default value
#
# Result:
# None
#
proc PossiblySet {name value} {
upvar $name V
if { ! [info exists V] } {
set V $value
}
}
# Input, Multiply, Add, Integrate, Output --
# Implement the actual operation
#
# Arguments:
# See the equivalent public procedures
#
# Result:
# Result of the operation
#
# Side effects:
# Only for Output: print to screen
#
proc Input {name func} {
upvar 1 t t
lappend ::update [list set $name [expr $func]]
}
proc Multiply {const name outname} {
upvar 1 t t
upvar 1 $name V
lappend ::update [list set $outname [expr {$const * $V}]]
}
proc Add {oper1 oper2 outname} {
upvar 1 $oper1 V1
upvar 1 $oper2 V2
lappend ::update [list set $outname [expr {$V1 + $V2}]]
}
proc Integrate {name outname} {
upvar 1 stepsize dt
upvar 1 $name V1
upvar 1 $outname V2
lappend ::update [list set $outname [expr {$V2 + $V1*$dt}]]
}
proc Output {name} {
upvar 1 $name V
lappend ::outbuffer $V
}
# loop --
# Simulate the system in a time loop
#
# Arguments:
# start Start time
# stop Stop time
# stepsize Time step size
#
# Result:
# None
#
# Side effects:
# Print on screen of the output variables
#
# To do:
# Remove all local variables
#
# Note:
# Simple Euler integration scheme - more advanced schemes
# left as an exercise.
#
proc loop {start stop stepsize} {
set t $start
puts "t $::title"
# PreparePlot $::title
while { $t < $stop+0.5*$stepsize } {
set ::outbuffer $t
foreach u $::update {
eval $u
}
set ::update {}
foreach m $::model {
eval $m
}
puts $::outbuffer
DrawResult $::outbuffer $::title
set t [expr {$t + $stepsize}]
}
}
# DrawResult --
# Draw the result
#
# Arguments:
# buffer New values
# title Names of the columns
#
# Result:
# None
#
# Side effects:
# Draw the line for the next step
#
proc DrawResult {buffer title} {
set t [lindex $buffer 0]
foreach v [lrange $buffer 1 end] n $title {
$::p plot $n $t $v
}
}
# PreparePlot --
# Prepare the plot (via Plotchart)
#
# Arguments:
# title Names of the columns
# xstart
# xstop
# ystart
# ystop
#
# Result:
# None
#
# Side effects:
# XY-plot prepared
#
proc preparePlot {xstart xstop ystart ystop} {
package require Tk
package require Plotchart
set canvas [canvas .c]
pack $canvas -fill both
set ::p [::Plotchart::createXYPlot $canvas \
[::Plotchart::determineScale $xstart $xstop] \
[::Plotchart::determineScale $ystart $ystop]]
foreach n $::title c {black blue green orange red magenta} {
$::p dataconfig $n -colour $c
}
}
# main --
# Define the simple equation above and run the system
#
input I {sin($t)}
integrate U uout 0.0
multiply -0.1 uout uscaled
add I uscaled U
output I
output uout
preparePlot 0.0 10.0 -2.0 2.0
loop 0.0 10.0 0.05