Polynomial fitting
Arjen Markus 2004-04-05: Knowing orthogonal polynomials like the Legendre family and others, and having played a bit with discrete Fourier transforms (see Discrete Fourier Transform) I thought I would try an analoguous technique for polynomials.
There is one practical difference with discrete Fourier transforms: it is difficult (but not impossible) to write down closed formulae for the polynomials to be used. I started with:
- The nodes or auxiliary points are x = k/N (where k = -m, -m+1, ..., m-1, m, N=2m+1, and similar - but different for even N)
- The poynomials must be orthogonal in the sense that the sum
m
Sum Pi(x)*Pj(x) = 0, if i != j
k=-m- The first two are simple:
P0(x) = 1
P1(x) = x- The third becomes troublesome already because you have to distinguish between even and odd N.
So, I decided to give up on this analytic approach and instead use a practical (numerical) one:
- I try to fit N data points
- The nodes for the polynomials are x = k, k=1,N
- The polynomials that I want to fit with are determined "on the fly", using a simple Gram-Schmidt orthogonalisation process and subsequent normalisation.
- Due to the orthogonality the fitting of the data becomes almost trivial, just as with the discrete Fourier transform.
(Improvements:
- Reduce the overhead of double computations - certain intermediate results are computed more than once
- The toString procedure does not take care of minus signs - I overlooked that possibility and was too lazy to repair that. Probably the best solution is to modify the string afterwards.)
# discrpol.tcl --
# A discrete polynomial transform:
# Just like with a discrete Fourier transform a series of data
# is fitted with orthogonal polynomials, the orthogonality being
# defined via sums over discrete (equidistant) points.
# This leads to sums of the type:
# N
# Sum k**p
# k=1
# which can be expressed in a closed form for any integer p,
# but the formulae get complicated and there is little system
# in them (well, there is a very complicated system in them).
#
# So, we compute the orthogonal polynomials "on the fly"
#
# Note:
# The polynomials are represented as a tagged list of
# coefficients. The independent coordinates are taken to be
# from 1 to N (the number of data)
namespace eval ::dpt {
# Make it exist
}
# EvalPolynomial --
# Evalute a polynomial at a given ordinate
#
# Arguments:
# coeffs The coefficients of the polynomial
# x The ordinate
# Result:
# Value of the polynomial at x
#
proc ::dpt::EvalPolynomial { coeffs x } {
set result 0.0
set px 1.0
foreach c $coeffs {
set result [expr {$result+$c*$px}]
set px [expr {$px*$x}]
}
return $result
}
# auxiliaryPoints --
# Return a list of auxiliary points (for evaluting the polynomials)
#
# Arguments:
# nodata Number of data
# Result:
# List of ordinates to evaluate the polynomials at
# Note:
# This procedure defines in fact the details of the polynomial
# fitting.
#
proc ::dpt::auxiliaryPoints { nodata } {
set xlist {}
for { set x 1 } { $x <= $nodata } { incr x } {
lappend xlist $x
}
return $xlist
}
# valuesPolynomial --
# Evalute a polynomial for a list of ordinates
#
# Arguments:
# polyn The polynomial
# xlist List of ordinates
# Result:
# Values of the polynomial at each ordinate as a list
#
proc ::dpt::valuesPolynomial { polyn xlist } {
set result {}
set coeffs [lrange $polyn 2 end]
foreach x $xlist {
lappend result [EvalPolynomial $coeffs $x]
}
return $result
}
# discreteNorm --
# Determine the (discrete) norm of a given polynomial
#
# Arguments:
# poly The coefficients of the polynomial
# Result:
# Norm of the polynomial (sqrt(sum(Poly(x)**2))
#
proc ::dpt::discreteNorm { poly } {
set nodata [lindex $poly 1]
set xlist [auxiliaryPoints $nodata]
set values [valuesPolynomial $poly $xlist]
set result [inproduct $values $values]
expr {sqrt($result)}
}
# inproduct --
# Determine the inproduct of two data vectors
#
# Arguments:
# data1 The values in the first vector
# data2 The values in the second vector
# Result:
# Inproduct
#
proc ::dpt::inproduct { data1 data2 } {
set result 0.0
foreach d1 $data1 d2 $data2 {
set result [expr {$result+$d1*$d2}]
}
return $result
}
# scalePolynomial --
# Scale a polynomial
#
# Arguments:
# poly The polynomial to be scaled
# factor The factor to be applied
# Result:
# New polynomial
#
proc ::dpt::scalePolynomial { poly factor } {
set newpoly [lrange $poly 0 1]
foreach c [lrange $poly 2 end] {
lappend newpoly [expr {$c*$factor}]
}
return $newpoly
}
# addPolynomials --
# Add two polynomials
#
# Arguments:
# poly1 The first polynomial
# poly2 The second polynomial
# Result:
# New polynomial
# Note:
# The two polynomials need not be of the same degree!
#
proc ::dpt::addPolynomials { poly1 poly2 } {
set newpoly [lrange $poly1 0 1]
foreach c1 [lrange $poly1 2 end] c2 [lrange $poly2 2 end] {
if { $c1 == {} } { set c1 0.0 }
if { $c2 == {} } { set c2 0.0 }
lappend newpoly [expr {$c1+$c2}]
}
return $newpoly
}
# axpyPolynomials --
# Add two polynomials and scale the first at the same time
#
# Arguments:
# factor Factor for scaling the first
# poly1 The first polynomial
# poly2 The second polynomial
# Result:
# New polynomial
# Note:
# The two polynomials need not be of the same degree!
#
proc ::dpt::axpyPolynomials { factor poly1 poly2 } {
set newpoly [lrange $poly1 0 1]
foreach c1 [lrange $poly1 2 end] c2 [lrange $poly2 2 end] {
if { $c1 == {} } { set c1 0.0 }
if { $c2 == {} } { set c2 0.0 }
lappend newpoly [expr {$factor*$c1+$c2}]
}
return $newpoly
}
# toString --
# Turn a polynomial into a readable string
#
# Arguments:
# poly The polynomial to be converted
# Result:
# String of the form 1.0 + 1.2*x + 3.0*x^2 ...
#
# Note:
# Not quite right yet - I forgot about minus signs ...
#
proc ::dpt::toString { poly } {
set string ""
set power -1
foreach c [lrange $poly 2 end] {
incr power
if { $c == 0 } { continue }
#
# Trick: leave out 1.00000
#
set cs "$c"
if { $cs != 1.0 || $power == 0 } {
append string "$cs"
if { $power != 0 } {
append string "*"
}
}
if { $power > 0 } {
append string "x"
}
if { $power > 1 } {
append string "^$power"
}
append string " + "
}
return [string range $string 0 end-3]
}
# orthogonalPolynomials --
# Build a list of N discretely orthogonal polynomials
#
# Arguments:
# nodata Number of data
# maxdegree Maximum degree
# Result:
# List of polynomials that are "discretely" orthogonal
# Note:
# This procedure uses an ordinary Gram-Schmidt algorithm
# to achieve the orthogonal (orthonormal) polynomials.
# It may not be ideal, but it is fairly straightforward.
# Improvements in terms of computational speed:
# Some things are calculated more than once, for instance
# the values of the polynomial at the auxiliary point.
#
proc ::dpt::orthogonalPolynomials { nodata maxdegree } {
set result {}
set v_points {}
#
# The first polynomial is simple: P(x) = c, where c = 1/sqrt(nodata)
#
set polyn [list DISCRETE-POLYNOMIAL $nodata 1.0]
set norm [expr {1.0/[discreteNorm $polyn]}]
lappend result [scalePolynomial $polyn $norm] ;# To get a norm 1
#
# The auxiliary points for which to evalue the polynomials
#
set xlist [auxiliaryPoints $nodata]
lappend v_points [valuesPolynomial [lindex $result 0] $xlist]
#
# From there we build up our polynomials
#
for { set degree 1 } { $degree <= $maxdegree } { incr degree } {
set polyn [linsert $polyn 1 0.0]
set newpolyn $polyn
foreach orthop $result orthov $v_points {
set coeff [inproduct $orthov [valuesPolynomial $newpolyn $xlist]]
set newpolyn [axpyPolynomials [expr {-$coeff}] $orthop $newpolyn]
}
#
# Normalise
#
set newpolyn [scalePolynomial $newpolyn [expr {1.0/[discreteNorm $newpolyn]}]]
lappend result $newpolyn
lappend v_points [valuesPolynomial $newpolyn $xlist]
}
return $result
}
# fittingPolynomial --
# Compute the best fitting (approximating) polynomial of given degree
#
# Arguments:
# data The data to be fitted
# maxdegree The maximum degree for the polynomial
# Result:
# New polynomial that fits the data
# Note:
# The procedure is fairly straightforward:
# - Compute the orthonormal polynomials first
# - Determine the coefficients for each
# - Sum the result
#
proc ::dpt::fittingPolynomial { data maxdegree } {
set nodata [llength $data]
set orthopols [orthogonalPolynomials $nodata $maxdegree]
#
# The auxiliary points for which to evalue the polynomials
#
set xlist [auxiliaryPoints $nodata]
set result [list DISCRETE-POLYNOMIAL 0.0]
foreach p $orthopols {
set coeff [inproduct [valuesPolynomial $p $xlist] $data]
set result [axpyPolynomials $coeff $p $result]
}
return $result
}
# testOrthonormality --
# Compute how well the list of polynomials fits orthonormality
#
# Arguments:
# nodata The number of data in the fits
# maxdegree The maximum degree for the polynomial
# Result:
# None
# Side effects:
# Printed report
#
proc ::dpt::testOrthonormality { nodata maxdegree } {
set orthopols [orthogonalPolynomials $nodata $maxdegree]
puts "Number of data points: $nodata"
puts "Discrete norm of the polynomials (should be 1)"
set degree 0
foreach p $orthopols {
puts "degree $degree: norm = [discreteNorm $p]"
incr degree
}
puts "Non-orthogonality between polynomials (inproduct should be zero)"
set degree 0
set xlist [auxiliaryPoints $nodata]
foreach p $orthopols {
set degree2 [expr {$degree+1}]
foreach q [lrange $orthopols $degree2 end] {
set inp [inproduct [valuesPolynomial $p $xlist] [valuesPolynomial $q $xlist]]
puts "degrees $degree and $degree2: inproduct = $inp"
incr degree2
}
incr degree
}
}
# a few tests ---
#
set polyn [list DISCRETE-POLYNOMIAL 10 1.0 0.0 2.0 1.0]
puts [::dpt::toString $polyn]
set polyn1 [list DISCRETE-POLYNOMIAL 10 1.0 2.0]
set polyn2 [list DISCRETE-POLYNOMIAL 10 0.0 0.0 2.0 1.0]
puts [::dpt::toString [::dpt::addPolynomials $polyn1 $polyn2]]
set orthopols [::dpt::orthogonalPolynomials 10 3]
foreach p $orthopols {
puts [::dpt::toString $p]
}
puts "Fit trivial data:"
puts "-1+x expected"
set data [list 0 1 2 3 4 5 6 7 8 9 10]
set result [::dpt::fittingPolynomial $data 3]
puts [::dpt::toString $result]
puts "1-2*x+x^2 expected"
set data [list 0 1 4 9 16 25 36 49 64 81 100]
set result [::dpt::fittingPolynomial $data 3]
puts [::dpt::toString $result]
puts "Test for quality of orthogonal polynomials"
::dpt::testOrthonormality 10 4
::dpt::testOrthonormality 100 10The results:
1.0 + 2.0*x^2 + x^3 1.0 + 2.0*x + 2.0*x^2 + x^3 0.316227766017 -0.605530070819 + 0.110096376513*x 0.957427107756 + -0.478713553878*x + 0.0435194139889*x^2 -1.54380482359 + 1.36927211043*x + -0.296885542998*x^2 + 0.017993063212*x^3 Fit trivial data: -1+x expected -1.0 + 1.0*x + 3.90981074709e-014*x^2 + -2.11315780976e-015*x^3 1-2*x+x^2 expected 1.0 + -2.0*x + 1.0*x^2 + -3.79690387208e-015*x^3 Test for quality of orthogonal polynomials Number of data points: 10 Discrete norm of the polynomials (should be 1) degree 0: norm = 1.0 degree 1: norm = 1.0 degree 2: norm = 1.0 degree 3: norm = 1.0 degree 4: norm = 1.0 Non-orthogonality between polynomials (inproduct should be zero) degrees 0 and 1: inproduct = -5.55111512313e-017 degrees 0 and 2: inproduct = -1.36002320517e-015 degrees 0 and 3: inproduct = 1.20181642416e-014 degrees 0 and 4: inproduct = -2.02504679692e-013 degrees 1 and 2: inproduct = -2.10942374679e-015 degrees 1 and 3: inproduct = 1.93178806285e-014 degrees 1 and 4: inproduct = -2.31370478332e-013 degrees 2 and 3: inproduct = 9.90874049478e-015 degrees 2 and 4: inproduct = -8.87345752432e-014 degrees 3 and 4: inproduct = -2.43693953905e-014 Number of data points: 100 Discrete norm of the polynomials (should be 1) degree 0: norm = 1.0 degree 1: norm = 1.0 degree 2: norm = 1.0 degree 3: norm = 1.0 degree 4: norm = 1.0 degree 5: norm = 1.0 degree 6: norm = 1.0 degree 7: norm = 1.0 degree 8: norm = 1.0 degree 9: norm = 1.00000000001 degree 10: norm = 1.00000000001 Non-orthogonality between polynomials (inproduct should be zero) degrees 0 and 1: inproduct = 1.2490009027e-016 degrees 0 and 2: inproduct = 1.21430643318e-016 degrees 0 and 3: inproduct = -6.71337985203e-015 degrees 0 and 4: inproduct = -1.0762224445e-014 degrees 0 and 5: inproduct = 7.17013254325e-013 degrees 0 and 6: inproduct = -9.62304888552e-012 degrees 0 and 7: inproduct = 9.26707738325e-011 degrees 0 and 8: inproduct = -7.20321007702e-010 degrees 0 and 9: inproduct = 4.39475776257e-009 degrees 0 and 10: inproduct = -1.81058440948e-008 degrees 1 and 2: inproduct = -2.77555756156e-017 degrees 1 and 3: inproduct = -4.71150896075e-015 degrees 1 and 4: inproduct = -1.44675937896e-014 degrees 1 and 5: inproduct = 4.85986251242e-013 degrees 1 and 6: inproduct = -6.81009415526e-012 degrees 1 and 7: inproduct = 7.36949667957e-011 degrees 1 and 8: inproduct = -6.32568483705e-010 degrees 1 and 9: inproduct = 4.16724826868e-009 degrees 1 and 10: inproduct = -1.84985766982e-008 degrees 2 and 3: inproduct = 9.36750677027e-016 ... degrees 8 and 9: inproduct = -3.20738435811e-011 degrees 8 and 10: inproduct = 8.70094343797e-010 degrees 9 and 10: inproduct = -3.22448748258e-010
TV: Isn't it so that except for special cases, N points span exactly one Nth degree polynomial Aix^i [No. You need N+1 points, since there are N+1 coefficients in an Nth degree polynomial. - Lars H] by solving for the Ai's, filling the points in, and that that solution arrives at the lagrange interpolation (I've looked it up, that's what it's called) polynomial solution? [Lagrange interpolation is one way to arrive at the unique polynomial passing through N+1 points. The formula is straightforward, but the coefficients with respect to the standard basis x^i of the interpolation polynomial are not readily apparent from this formula. An alternative is Newton interpolation, where the points are added one at a time. LH again.] In fact the question mark isn't needed: for any N+1 data points there is exactly 1 polynomial of degree <=N which passes through those points, so when the polynomial is to pass through N+1 general (yi,xi) with x,y el. |R, 0<i<N, there is one and only one solution according to the legendre polynomial, which is a fraction of N linear factors by N normalisation factors.
Polynomials as basis either to span a solution or interpolation space is of course interesting. Maybe look at what's sort of known in the computer graphics community, I found a nice overview (starts at page 3) at Curves and Surfaces , Durand and Cutler, Intro to Computer Graphics (alternate ), Fall 2003.
An orthogonal/orthonomal power base in Hilbert or Fock space (in mathematica/physics) usually involves an integral measure to determine correlation/orthogonality, taking the whole (continuous) polynomial into account over some interval, not just the control or data points.
N-th degree polynomials usually start to get mighty unstable and annoying for N like 20 or 100, and many problems are of lower degree. So usually one wants a fitting polynomial, of which of course well known ones are splines, partial least squares approximations, beziers (see above link).
For CAGD applications, there are power basises which maintain what is called the 'partition of unity', which means the basis functions add up to one everywhere on the curve, and are used to weigh the vectors spanning the curve or surface (I think it is also in the above link).
I'm sure when polynomials and interpolation are being discussed, each engineer (and of course everybody with interest) should know about Taylor Expansion as phenomena/method.
Something probably should be said about the theory of Generalized Fourier series here, because both this page and Discrete Fourier Transform touches upon the subject.
The basic idea is to define an inner product on some set of functions, usually the set of all real-valued (but complex-valued works fine too) functions on some interval [a,b] that satisfy some "smoothness" condition (such as continuity, Riemann integrability, or having everywhere continuous first derivative). If f and g are two such functions, then their inner product <f,g> is given by an integral on the form
\int_a^b f(x) g(x) W(x) dx
where W is a "weight function". For the inner products that give rise to trigonometric Fourier series or Legrende-Fourier series this function is constant, but in many standard families of orthogonal polynomials the orthogonality is with respect to a non-constant weight. If the functions are complex-valued then one needs to complex conjugate one of the functions, so that the inner product formula becomes
\int_a^b f(x) \overline{g(x)} W(x) dxFinally, it is possible to integrate with respect to a general measure instead of using the Riemann integral as shown above. This makes it possible to treat inner products defined using sums as special cases of inner products defined using integrals, thus unifying the theoretical machinery. The discreteNorm procedure above is the norm corresponding to the inner product <f,g> defined by the integral
\int_1^N f(x) g(x) d\mu(x)
where \mu is the discrete measure with weight 1 at points 1, 2, ..., N and weight 0 everywhere else.
Once the inner product is defined, it is all Linear Algebra. Forget that you started with functions, because from this point on they will just be some kind of vectors.
Recall that the orthogonal projection of a vector f onto a vector u, with respect to the inner product <.,.>, is the vector
<f,u> <u,u>^{-1} uIf u_1, ..., u_n is a sequence of pairwise orthogonal vectors, then the projection of f onto the space spanned by these vectors is
g = \sum_{k=1}^n <f,u_n> <u_n,u_n>^{-1} u_nTwo noteworthy properties of this g are: (i) It is orthogonal to f-g, i.e.,
<g, f-g> = 0
and (ii) in the space spanned by u_1,...,u_n, the point g is the one that is closest to f, i.e.,
<f-g, f-g>
is minimal. This is the sense in which approximations obtained via orthogonal projection / Fourier series are the best possible: the norm of the "approximation error" f-g is minimal.
If u_1,u_2,... is any sequence (possibly infinite) of orthogonal vectors, then one defines the generalised Fourier coefficients of a vector f with respect to this sequence to be the numbers
c_n = <f,u_n> / <u_n,u_n> for n = 1,2,...
The corresponding generalised Fourier series is
g = \sum_n c_n u_n
Clearly any partial sum
\sum_{k=1}^n c_k u_kof this series is simply the orthogonal projection of f onto the subspace spanned by u_1,...,u_n. A sequence u_1,u_2,... is said to be complete if it follows that f=0 whenever all the generalised Fourier coefficients of f with respect to u_1,u_2,... are 0. The generalised Fourier series of some f with respect to a complete orthogonal sequence always converges in norm to f. And that's all there is to it!
The practical use one can have of this is that if your orthogonal sequence is well chosen then even rather small partial sums (i.e., orthogonal projections onto some low-dimensional subspace) can capture much of the interesting information in your input f, while it tends to ignore the noise. It can also be used for various kinds of curve-fitting problems. For example, if it is required to approximate a function on an interval by a low degree polynomial, then taking a partial sum of some generalised Fourier series of that function often does a stunningly good job (often with a far smaller maximal error than any Taylor polynomial of that function).
Example. Consider the problem of approximating f(x) = arctan x with polynomials on some interval containing x=0. (Friends of rational approximation will object that this is not a very bright thing to do, because arctan is a very non-polynomial function. Indeed if the aim is to find something closely approximating arctan on the whole real line then one may be better off with rational or algebraic approximants, but the subject of this page is polynomial fitting.)
The first thing people tend to try for this is using the Taylor series
\arctan x = \sum_{k=0}^infty x^{2k+1} (-1)^k / (2k+1) =
= x - x^3/3 + x^5/5 - x^7/7 + ...taking the polynomials formed by the first n terms of the series as approximations. A plot of arctan and these approximations look as
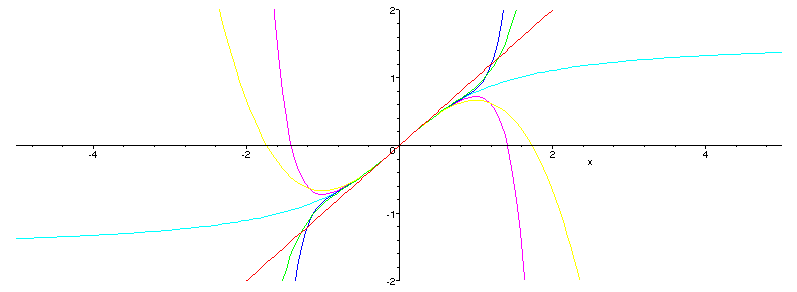
And a plot of the approximation errors is

It is very good near x=0, but as |x| gets closer to 1 the error shoots off. This is no coincidence; 1 is the radius of convergence of this Taylor series, which means that the rate of convergence drops rather quickly as
If we're going to stick with the interval [-1,1] then the obvious choice for orthogonal polynomials are the Legendre polynomials P_n(x). These are orthogonal with respect to the inner product
<f,g> = \int_{-1}^1 f(x) g(x) dxand can be computed using the recursion
P_0(x) = 1
P_1(x) = x
P_n(x) = ( (2n-1) x P_{n-1}(x) - (n-1) P_{n-2}(x) ) / n for n>1.All corresponding even numbered generalised Fourier coefficients are 0 (this is an even/odd function thing; arctan is odd, and all even numbered Legrendre polynomials are even), and the first few odd numbered coefficients are
c_1 = 0.8561944905 c_3 = -0.08001405300 c_5 = 0.01054242750 c_7 = -0.001524225000 c_9 = 0.0002308500000
The first five distinct partial sums of the corresponding generalised Fourier series are thus
g_1(x) = 0.8561944905*x g_3(x) = 0.9762155700*x - 0.2000351325*x^3 g_5(x) = 0.9959826216*x - 0.2922813731*x^3 + 0.08302161656*x^5 g_7(x) = 0.9993168638*x - 0.3222895528*x^3 + 0.1490396119*x^5 - 0.04086828281*x^7 g_9(x) = 0.9998849712*x - 0.3306217950*x^3 + 0.1815353564*x^5 - 0.08729077500*x^7 + 0.02192173242*x^9
Plotting these with arctan, show a picture similar to the above
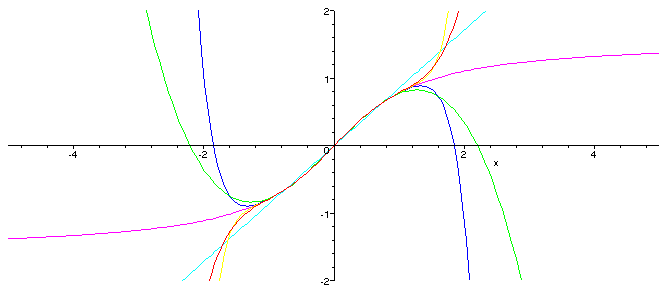
but a plot of the errors demonstrate that these do a much better job at covering the whole interval [-1,1].

In fact, most of them cover a bit more than this interval.
Another family of orthogonal polynomials, which will produce a result that in some ways is even nicer, are the Hermite polynomials H_n(x). These are orthogonal with respect to the inner product
<f,g> = \int_{-\infty}^\infty f(x) g(x) \exp(-x^2) dxi.e., the integral is over the whole real line, but there is a weight that strongly reduces the influence of points far from x=0. The Hermite polynomials can be computed using the recursion
H_0(x) = 1
H_1(x) = 2x
H_n(x) = 2x H_{n-1}(x) - 2(n-1) H_{n-2}(x) for n>1.Again all corresponding even numbered generalised Fourier coefficients for arctan are 0, whereas the first few odd numbered coefficients are
c_1 = 0.3789360782 c_3 = -0.01140068623 c_5 = 0.0004162197431 c_7 = -0.00001378823126 c_9 = 0.4039831088e-6
The first five distinct partial sums of the corresponding generalised Fourier series are thus
g_1(x) = 0.7578721564*x g_3(x) = 0.8946803912*x - 0.9120548984e-1*x^3 g_5(x) = 0.9446267604*x - 0.1578006487*x^3 + 0.1331903178e-1*x^5 g_7(x) = 0.9677909889*x - 0.2041291058*x^3 + 0.3185041459e-1*x^5 - 0.1764893601e-2*x^7 g_9(x) = 0.9800074381*x - 0.2367063036*x^3 + 0.5139673333e-1*x^5 - 0.5488001932e-2*x^7 + 0.2068393517e-3*x^9
A plot shows that these stay close to arctan on an interval up to three times as large

and a plot of the errors shows that these manages to stay pretty small throughout

A final word: There is nothing special with polynomials (other than that you only need plus, minus, and times to evaluate them), and there is nothing special with the classical families of orthogonal polynomials (other than that someone has gone through the work of working out the formulae for them). If you're just in it for the numerics then you can Gram--Schmidt away, starting from any family of functions and any inner product.
jmp: If the issue is data fitting with polynomials (*not* data interpolation), what about B-splines? People seldom know that splines can also be used to fit data, not only to draw smooth curves for graphical applications. Moreover there is an explicit solution for the fitting problem which relies on linear problem solving (provided there is enough data to invert matrices). I can not detail what this consists in because I prefer using the Matlab spline toolbox! What are the spline advantages? You can choose the polynomial order and the knot position that best correspond to your data. My experience is that this is a very interesting replacement for global polynomial fitting and linear (lowpass) filtering: knots positions usually match the data "waves" you want to keep so that algorithm tuning is easier. Just tune the spline (= polynomial) order to make fitted data more or less smooth. Unfortunately I don't have a web link dealing with this issue, but I know there is a reference book on spline: A practical guide to splines (de Boor). This is full of formulas...
AM 2004-04-20: Sure, splines do have significant advantages when it comes to interpolation and fitting. The above merely decribes one possible way. Besides B-splines, cubic splines seem useful too and a lot easier as far as the maths is concerned.
However, they do lack the nice physical interpretation of the various components in a Fourier series (sines/cosines, orthogonal polynomials ....) - that of "energy"
TV: Just to repeat: for a number of points, there is exactly one fitting lagramnge polynomial, for which there exists a closed form formula (a fraction with terms for the zeros in the enumerator and normalizing factors in the denominator), so no real need to do a lot of complicated approximation stuff. Probably with that one could to least squares for curve fitting where the degree of the curve is lower than lagrange polynomial corresponding directly to the data points.
AM: Hm, if monsieur Lagrange's interpolation method had been perfect, nobody would have bothered inventing another one :). The main use of that method, AFAIK, is theoretical - the practical use is severely limited by the fact that there is no useful bound on the error you make. There is no pointwise convergence. So, other methods - many other methods - have been invented, all with their own limitations and awkwardnesses.
TV: Well, then just the mathematical point: your method (when I interpret right) simply converges to lagrange, and only that, because the whole solving of the orhtogonalness etc. in the end can be proven to have only one theoretical solution: lagrange (unless I miss something). Not that that is bad, it just seems like a long way around.
AM: Sorry, you are misinterpreting the mathematics (I might almost say the physics) of the approximation: Lagrange's method gives an exact match on selected points, but there is no guarantee as to what happens in between, the Fourier series using orthogonal functions approximates in a completely different sense: it minimizes some integral or sum. So, this is where the classic problem of Fourier analysis pops up: for what classes of functions does the Fourier series also converge pointwise? That is answered in any self-respecting text book on Fourier analysis :).
TV: Arjen, I didn't want to start a rant, I'm as you probably know, edified enough in the area not to need to prove myself on this, but the point which I brought forward is simple, and in the subject area IMO relevant. IF one, as I think is stated above:
- I try to fit N data points
- The nodes for the polynomials are x = k, k=1,N
takes N (forgiving the +1 or not) data points in general, then like a line is defined by two points, a quadric defined by 3, etc, the polynomial which you try to derive/compute in some way is already without free parameters defined by the laGrange polynomial, which is available in easy enough to automate closed form.
Unless I miss some other insight, I think that is relevant to notice, and makes the above as I suggested.
Apart from that, If you want to project your polynomial, any polynomial, unto some orthogonal basis, after you define the measure of orthogonality (usually some fitting form of inproducts which are then set to zero for all combinations of the basis vectors/polynomials except projections on itself), that of course can be a good idea, and basises like that under common inproducts (like functional integral inspired) exist and can be presented in closed for expressions. Refactoring the polynomial into a sum or even product depends on the choice of basis, and yours seems to be directly related to you datapoints, which again IMO makes not too much sense, I'd go for a more general basis.
AM: I think I see now where you misunderstand the above procedure:
- The orthogonal polynomials as defined for my inproduct are not easily determined by analytical means.
- So, rather than go through all the tedious motions, I let one part of the script determine the coefficients of these polynomials (just a Gram-Schmidt orthogonalisation process, it has nothing to do with factoring the polynomials :))
- The data are known only at the given points and I wanted to avoid some interpolation between them.
- So, it is very comparable to a Discrete Fourier Transform, in that it approximates at certain points. Therefore I can choose the level of approximation - use a third-degree polynomial even though I have one hundred data points. You can not do that with Lagrange's method.
TV: Well, final remark for now (you don't make the subject sound interesting enough, orthogonal polynomials are not strange in physics), the theory above (which I read when I saw the page, which of course should give interesting material for others to use, given the title, states what I Cut and Pasted, N data points, I didn't read N1 and N2 or something, so I assumed you fit N data points to a N-1th degree (give or take a 1...) polynomial. In that case, there is only one, and exactly one, and no more than one, solution (or none, for some degenerate cases like point in a vertical lines), which can be found using not so hard formula (depending on your background).
That's all my remark was about.
AM: Theo, yes, it finally dawned to me yesterday, when I went home ;). Whereas I was thinking in terms of the approximating polynomial converging to the data points as its degree rises, you were thinking of the polynomial converging the polynomial that goes through all the data points - indeed, the polynomial given directly by the Lagrange interpolation.
Whereas I have learned about such polynomial families as those made famous by Legendre and Hermite, I never encountered a proper treatise of the discrete case, apart from the discrete Fourier transform with sines and cosines...