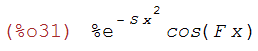Scripting formula manipulations in Maxima with results in PostgreSQL
We take two tcl access scripts, presuming presence of Maxima and PostgreSQL on a system or, in the latter case, on some system in the network:
proc domaxima { {m} } {
set t "display2d:false;\n$m;"
# return [string range [exec maxima << $t | tail -2 ] 6 end-7]
return [string range [exec maxima -q << $t ] 32 end-7]
#return [exec maxima --real-quiet << $t ]
}
proc dosql {s} {
global db
if {[catch {pg_exec $db $s} reply]} {
puts "sql error : $reply,[pg_result $reply -error]"
return "Error"
}
if {[pg_result $reply -status] == "PGRES_COMMAND_OK"} {
return {}
}
if {[pg_result $reply -status] != "PGRES_TUPLES_OK"} {
puts "sql error: [pg_result $reply -error]"
return "Error"
}
return [pg_result $reply -llist]
# pg_result $reply -clear
return
}
# You could use another with similar results, it appears:
package require pgintcl
# connect to your sql server:
set db [pg_connect -conninfo [list host = 192.168.0.1 user = zxy dbname = somedb password = 0x987654]]
# Now create a table for formulas
dosql "create table formula (f varchar(256))"Now we can try to make a nice database with formulas:
dosql "insert into formula values ([pg_quote "x^2"])" dosql "insert into formula values ([pg_quote "x^3"])"
But we can also use maxima to help us, for instance the optimizer will reorder terms and at request also simplify so we can keep formulas unique for instance:
dosql "insert into formula values ([pg_quote [domaxima "x^4"]])" dosql "insert into formula values ([pg_quote [domaxima "x^3"]])"
Now lets look at the nice lil' list of math work:
foreach i [dosql "select distinct f from formula"] {puts |$i}
|x^2
|x^3
|x^4A more interesting example, a list of repeated derivatives of a products of two functions, a well known formula for case 1:
dosql "create table derivatives (ref varchar(64), f varchar(10000), df varchar(10000))" set i 1; set fo "q(x)*r(x)"; dosql "insert into derivatives values ( [pg_quote "prod$i"], [pg_quote [domaxima $fo]], [pg_quote [domaxima "diff($fo)"]] )" incr i; set fo "diff($fo)"; dosql "insert into derivatives values ( [pg_quote "prod$i"], [pg_quote [domaxima $fo]], [pg_quote [domaxima "diff($fo)"]] )" incr i; set fo "diff($fo)"; dosql "insert into derivatives values ( [pg_quote "prod$i"], [pg_quote [domaxima $fo]], [pg_quote [domaxima "diff($fo)"]] )" incr i; set fo "diff($fo)"; dosql "insert into derivatives values ( [pg_quote "prod$i"], [pg_quote [domaxima $fo]], [pg_quote [domaxima "diff($fo)"]] )"
Of course that could be easily put in a loop, but it's to prove the principle. Now:
% foreach i [dosql "select * from derivatives"] {puts $i}
prod1 q(x)*r(x) (q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))*del(x)
prod2 (q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))*del(x) {((q(x)*'diff(r(x),x,2)+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))*'diff(del(x),x,1))
*del(x)}
prod3 {((q(x)*'diff(r(x),x,2)+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))*'diff(del(x),x,1))
*del(x)} {(((q(x)*'diff(r(x),x,3)+3*'diff(q(x),x,1)*'diff(r(x),x,2)
+3*'diff(q(x),x,2)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,3))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))*'diff(del(x),x,2)
+2*(q(x)*'diff(r(x),x,2)+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))*'diff(del(x),x,1))
*del(x)
+'diff(del(x),x,1)*((q(x)*'diff(r(x),x,2)
+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))
*'diff(del(x),x,1)))
*del(x)}
prod4 {(((q(x)*'diff(r(x),x,3)+3*'diff(q(x),x,1)*'diff(r(x),x,2)
+3*'diff(q(x),x,2)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,3))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))*'diff(del(x),x,2)
+2*(q(x)*'diff(r(x),x,2)+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))*'diff(del(x),x,1))
*del(x)
+'diff(del(x),x,1)*((q(x)*'diff(r(x),x,2)
+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))
*'diff(del(x),x,1)))
*del(x)} {((((q(x)*'diff(r(x),x,4)+4*'diff(q(x),x,1)*'diff(r(x),x,3)
+6*'diff(q(x),x,2)*'diff(r(x),x,2)
+4*'diff(q(x),x,3)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,4))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))*'diff(del(x),x,3)
+3*(q(x)*'diff(r(x),x,2)+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))*'diff(del(x),x,2)
+3*(q(x)*'diff(r(x),x,3)+3*'diff(q(x),x,1)*'diff(r(x),x,2)
+3*'diff(q(x),x,2)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,3))*'diff(del(x),x,1))
*del(x)
+2*'diff(del(x),x,1)
*((q(x)*'diff(r(x),x,3)+3*'diff(q(x),x,1)*'diff(r(x),x,2)
+3*'diff(q(x),x,2)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,3))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))*'diff(del(x),x,2)
+2*(q(x)*'diff(r(x),x,2)+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))*'diff(del(x),x,1))
+'diff(del(x),x,2)*((q(x)*'diff(r(x),x,2)
+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))
*'diff(del(x),x,1)))
*del(x)
+'diff(del(x),x,1)*(((q(x)*'diff(r(x),x,3)
+3*'diff(q(x),x,1)*'diff(r(x),x,2)
+3*'diff(q(x),x,2)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,3))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))
*'diff(del(x),x,2)
+2*(q(x)*'diff(r(x),x,2)
+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))*'diff(del(x),x,1))
*del(x)
+'diff(del(x),x,1)
*((q(x)*'diff(r(x),x,2)
+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))
*'diff(del(x),x,1))))
*del(x)}More intelligently we can now look up in our little database what the general form is of a certain derivative of a product of functions, and what the original was from that derivative (the integral except for a constant), for instance:
(Tcl) 69 % dosql "select ref, f from derivatives where df = [pg_quote "(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))*del(x)"]"
{prod1 q(x)*r(x)}Or case 4:
dosql "select ref from derivatives where df = [pg_quote [domaxima "((((q(x)*'diff(r(x),x,4)+4*'diff(q(x),x,1)*'diff(r(x),x,3)
+6*'diff(q(x),x,2)*'diff(r(x),x,2)
+4*'diff(q(x),x,3)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,4))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))*'diff(del(x),x,3)
+3*(q(x)*'diff(r(x),x,2)+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))*'diff(del(x),x,2)
+3*(q(x)*'diff(r(x),x,3)+3*'diff(q(x),x,1)*'diff(r(x),x,2)
+3*'diff(q(x),x,2)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,3))*'diff(del(x),x,1))
*del(x)
+2*'diff(del(x),x,1)
*((q(x)*'diff(r(x),x,3)+3*'diff(q(x),x,1)*'diff(r(x),x,2)
+3*'diff(q(x),x,2)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,3))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))*'diff(del(x),x,2)
+2*(q(x)*'diff(r(x),x,2)+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))*'diff(del(x),x,1))
+'diff(del(x),x,2)*((q(x)*'diff(r(x),x,2)
+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))
*'diff(del(x),x,1)))
*del(x)
+'diff(del(x),x,1)*(((q(x)*'diff(r(x),x,3)
+3*'diff(q(x),x,1)*'diff(r(x),x,2)
+3*'diff(q(x),x,2)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,3))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))
*'diff(del(x),x,2)
+2*(q(x)*'diff(r(x),x,2)
+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))*'diff(del(x),x,1))
*del(x)
+'diff(del(x),x,1)
*((q(x)*'diff(r(x),x,2)
+2*'diff(q(x),x,1)*'diff(r(x),x,1)
+r(x)*'diff(q(x),x,2))
*del(x)
+(q(x)*'diff(r(x),x,1)+r(x)*'diff(q(x),x,1))
*'diff(del(x),x,1))))
*del(x)"]]"
prod4It finds the correct f for df, with the help of an additional 'domaxima' it doesn't matter what the formatting of the text of the formula is. Try for yourself.
Another dual application script tryout for the scientifically oriented which in the longer run could prove useful: a set of integral (Fourier - type) transformed functions in the database.
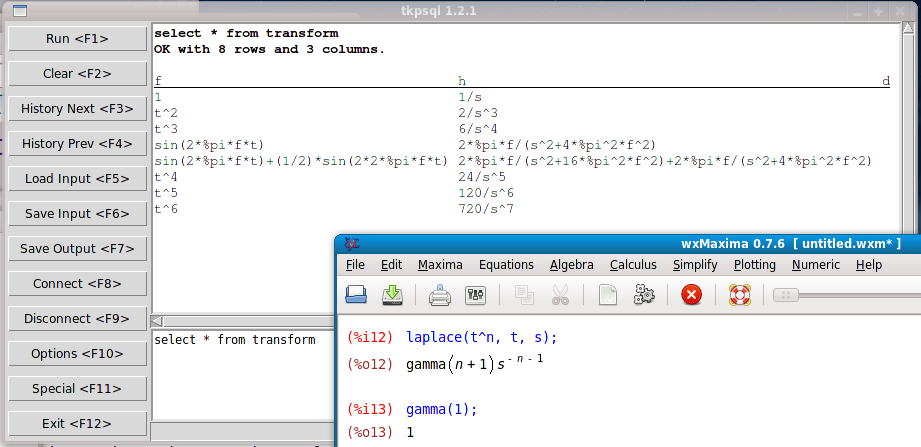
# create a new table dosql "create table transform (f text, h text, d text)" # try it out dosql "insert into transform values (1, 1/s)" #or better (and a unique definition of the table could be good,too): dosql "insert into transform values ([pg_quote 1], [pg_quote 1/s])"
This should do the same, but compute the transformation automatically:
domaxima "laplace(1, t, s)" 1/s
Correct. Let's populate a nice LaPlace transform table letting the transforms be computed automatically (the description remains NULL for the moment):
foreach fo "t^2 t^3 t^4 t^5 t^6 sin(2*%pi*f*t) sin(2*%pi*f*t)+(1/2)*sin(2*2*%pi*f*t) " {
dosql "insert into transform values ([pg_quote $fo], [pg_quote [domaxima "laplace($fo, t, s)"]] )"
}
dosql "select h from transform where f like [pg_quote "t^%"]"
dosql "select h from transform where f = [pg_quote "sin(2*%pi*f*t)+(1/2)*sin(2*2*%pi*f*t)"]"I've made a ~/.maxima/maxima-init.mac file with
assume (n>0);
check with (from the tcl console)
domaxima facts()
to get certain transforms to work with parameter n, which otherwise would call for an interactive entry which hangs the maxima procedure. Of course those defines then hold for all maxima invokations, so beware. A change to the simple maxima wrapper proc isn't needed, the output remain the same. In case you make that precaution, t^n can be added to the above list, which gives a gamma function as result.
Because we have these facilities now handily available at tcl (console) level, we can also pick La Place transformed formulas from the database (the SQL table) and perform an automatic inverse transform with Maxima, and we should get the same as the original t-function!
domaxima "ilt([dosql "select h from transform where f like [pg_quote "t^6"]"],s,t)"
That works, if you want exercise, you could make a loop of this over all formulas. Of course, which is a mathematical exercise, there are issues with the integrals involved, so some assumptions must be made.
The result in postgres:
(sor) Instead of centralizing ourselves like a bad opportunist New Yorker (they have funny commercials at CNN about that) as to go west through the Bad Mountains and wanting help for that instead of enjoying the Mississippi and the nice plains, we have little fun here with making a few menus and prepare ourselves On the Road Again on route 66 for some flying Tcl applications without doing bad to anyone. (end of rant) After all, Tcl is Free and Open Source software!
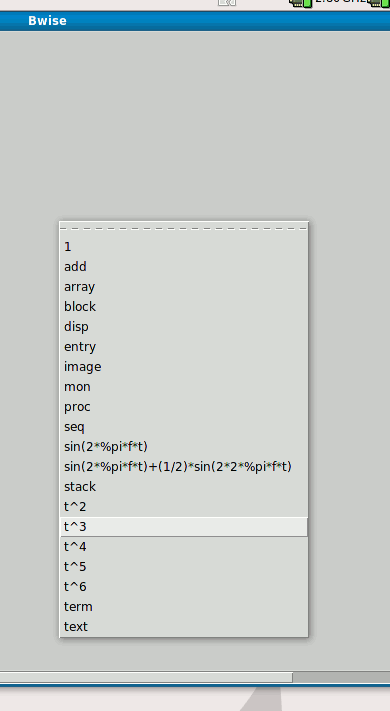
The menus are not easy to remember, and I seem to recall people wanting to go OO just because of lack of easy introspection and what in my scientific and indusrially oriented background was called and known as 'claim culture'. Luckily, the Tcl origins were not unlike Postgres or so: straight, professional, and fun because free of all those types of considerations, so lets try to make a menu based on a sql query, which given the above work (some find it a joy to work) is of course easy to do.
I just tried making an additional box (in Tk) for a menu above the BWise canvas, but that isn't easy enough unless I restart, so I use an easy method: defining procs in bwise which start with 'new' (and deleting them with rename, which was not easy to find in page titles here, but the world wide google google database pointed quickly to an ActiveState manual page, which is newer than that part of bwise):
foreach i [
dosql "select f from transform order by f"
] {
proc new$i {} {}
}and conversely:
foreach i [
dosql "select f from transform order by f"
] {
rename new$i {}
}Now lets make something with that 3 application setup and see what information that gives us, and maybe add some C programs, because, as it is written in a well known Tcl book (which I received after driving the writer to holland and in all honesty never looked into) "The best computer programmers are astonishingly more productive than average. They use good tools, and they use them well." I think that's a great adagio and must be on the mind of the writers of C, VHDL (tcl is/was used a lot in EE), and books on advanced unix programming. I suppose I want to be able to be opportunist too when I program fun stuff, but then again I've been accused of reading nuclear physics books before sleepy time by colleges in the past. Actual ones, that is, not biographies, and so I guess I might aim for high standards when I'm interested.
Feel free to check typos...
Oh for insterested people these experiments appear to work fine on Linux (Fedora 8/64 or 10/64) with PostgreSQL 8.2.5 or 8.3 something and tcl 8.5 or 8.6 with pgintcl 3.0.2 and some recent bwise. The tcl things run fine on a XPpro machine being connected over a network too. It appears there is a postgres for XP, too, I'll report when that works for me.
An application I just tried out: integrals of derivatives of the boson and fermion basis functions, e.g.
maxima can integrate the second derivative of this function back to the first derivative, but not the first to the origal function, and it depends on simplifications/reorderings of terms, so it can be good to recognize certain classes of such derivatives. Important theory, but I'm not currently familiar with that body of mathematics: I know it can be handy to compose formulas, whic can be done with bwise and to recognize them, just like there are quite a few known solutions to types of DEs.
To remember manipulations easier and centrally, I've made a history table which can contain all succesfully executed sql commands with timestamp on the sql server:
proc dosql { {s} } {
global db
if {[catch {pg_exec $db $s} reply]} {
puts "sql error : $reply,[pg_result $reply -error]"
return "Error"
}
if {[pg_result $reply -status] == "PGRES_COMMAND_OK"} {
catch {pg_exec $db "insert into history values (DEFAULT, [pg_quote $s] , 'now' , NULL)"}
return {}
}
if {[pg_result $reply -status] != "PGRES_TUPLES_OK"} {
puts "sql error: [pg_result $reply -error]"
return "Error"
}
set res [pg_result $reply -llist]
catch {pg_exec $db "insert into history values (DEFAULT, [pg_quote $s] , 'now' , NULL)"}
return $res
# we only put non-errors in the history
# pg_result $reply -clear
return
}
# once only:
dosql "create table history (i serial, l text, date timestamp , comment text)"Now we can for instance
dosql "select date,l from history"
Or
set im [dosql "select max(i) from history "]
puts " last entry #: $im"
78
% foreach i [dosql "select i,date,l from history where i > $im order by i asc"] {puts $i}
76 {2009-04-24 03:48:27.118317} {select l from history where i > 66 order by i asc}
77 {2009-04-24 03:49:15.686698} {select i,date,l from history where i > 66 order by i asc}
78 {2009-04-24 03:49:36.509501} {select i,date,l from history where i > 75 order by i asc}Short:
dosql "select i,date,l from history order by i desc limit 3"
handy with wildcard:
dosql "select l from history where l like 'create%' "
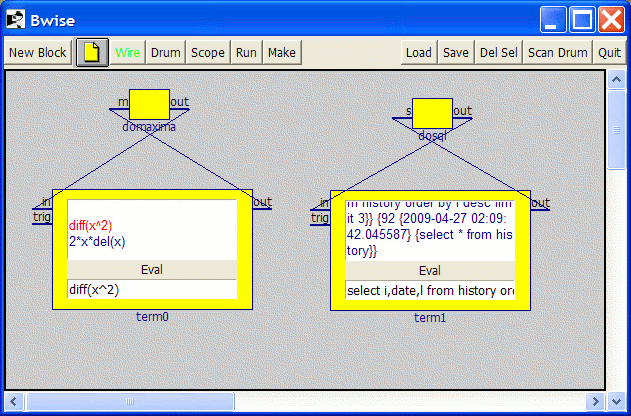
When using the stuff from the Latest Bwise or as here refered to, it is possible to simply play with maxima and sql, simply select domaxima and dosql respectively from the functions list, and press the Block button for each, and drag the resulting blocks on the bwise canvas, and connect them with a 'term' block from the bwise popup menu:
Isse simpel.
TV Oct 30 '10 I played a bit with the above derivative table, and made it longer, up to a megabyte formula size:
while {[string length $fo] < 1000000} {
dosql "insert into derivatives2 values ( [pg_quote "[incr i]"], [pg_quote [domaxima $fo]], [pg_quote [set fo [domaxima "diff($fo)"]]] )" ;
}and I´ve put the same data in my built in bwise in core database. I used two posgresql servers, on on the same (windows XP pro) machine running Tcl/Tk 8.5.1 with sql 8.3 and another on a Fedora 12/64 machine with a recent 8.4.5 postgresql (but at the same time showing a fast moving HD h264 movie).
The results (normally the Linux sql is about twice as fast as the windows):
(Tcl) 360 % time {puts [string length [lindex [ lindex [dosql "select f from derivatives2 where f = [pg_quote "$rr"]"] 0] 0]]}
205614
114274 microseconds per iteration
(Tcl) 361 % time {puts [string length [lindex [ lindex [dosql "select f from derivatives2 where f = [pg_quote "$rr"]"] 0] 0]]}
205614
115478 microseconds per iteration
(Tcl) 362 % time {puts [string length [lindex [ lindex [dosql2 "select f from derivatives2 where f = [pg_quote "$rr"]"] 0] 0]]}
205614
269187 microseconds per iteration
(Tcl) 363 % time {puts [string length [lindex [ lindex [dosql2 "select f from derivatives2 where f = [pg_quote "$rr"]"] 0] 0]]}
205614
83249 microseconds per iteration
(Tcl) 364 % time {puts [string length [lindex [lindex [dbsearch $rr f] 0] 2]]}
205614
346893 microseconds per iteration
(Tcl) 365 % time {puts [string length [lindex [lindex [dbsearch $rr f] 0] 2]]}
205614
342074 microseconds per iterationClearly, storing the data and doing the search on the Linux machine is normally fastest, and the tcl in-memory single-variable database is generally slower than the sql search, but I would have to check the exact searching I do in there. The formula I searched for is the 9th in a list of subsequent product-term derivatives, and the lists were ordered in ascending order.