Solving a wave propagation problem with the Tensor package
Arjen Markus (7 december 2010) After a demonstration of "OpenFOAM" yesterday I knew I could not postpone this anymore: I have wanted to experiment with the Tensor package and NAP for a long time now, to see how easy it is to solve partial differential equations with them.
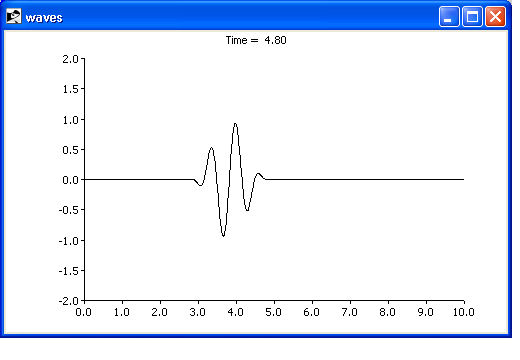
Here is my small-scale experiment with the Tensor package: solving the one-dimensional wave equation. The boundary conditions: left a prescribed excitation (h=h(t)) and right a fully reflexive wall (u=0). The function h(t) describes a compact wave train.
Not all is settled yet, but I thought I'd wikify it anyway.
# waves.tcl --
# Simulate a one-dimensional wave packet:
# - Two quantities related via first-order
# equations
# - Initial condition: a block
# - The boundary conditions are fully reflexive
# - implemented via u=0 on the boundary
# But the left boundary has a prescribed height
# - The grid is staggered (u and h on different points)
#
# Note:
# I am not fully satisfied with the implementation of the boundary conditions.
# This requires further attention!
#
package require Tk
package require Plotchart
package require Tensor
# nextTime --
# Compute the result for the next time
#
# Arguments:
# None
#
# Side effects:
# Tensor u and h updated
#
proc nextTime {} {
set ucoeff [expr {$::velocity * $::deltt / $::deltx}]
set hcoeff [expr {$::deltt / $::deltx}]
set rfrict [expr {1.0 - $::friction * $::deltt}]
set end [expr {$::number-1}]
set endm1 [expr {$::number-2}]
set endm2 [expr {$::number-3}]
set endp1 $::number
#
# Bounds depend on the type of boundary condition - unfortunately
#
::tensor::expr "u(i=1:$endm1) = $rfrict * u(i=1:$endm1) - $ucoeff * (h(i=1:$endm1) - h(i=0:$endm2))"
::tensor::expr "h(i=1:$end) = h(i=1:$end) - $hcoeff * (u(i=2:$endp1) - u(i=1:$end))"
}
# setBoundaryConditions --
# Set the boundary conditions - almost trivial in this case
#
# Arguments:
# time Time in the computation
#
# Side effects:
# Tensor u is updated
#
proc setBoundaryConditions {time} {
set end $::number
set endm1 [expr {$end-1}]
#
# A block boundary condition like this is too severe for the
# simple scheme I implemented. So use a smoother one instead
#
if { $time < 2.0 } {
set hvalue 1.0
} else {
set hvalue 0.0
}
if { $time < 2.0 } {
set hvalue [expr {0.5*(1.0-cos(3.1415926*$time)) * sin(3.0*3.1415926*$time)}]
} else {
set hvalue 0.0
}
h section 0 = scalar $hvalue
h section $end = scalar [h section $endm1]
u section 0 = scalar 0.0
u section $end = scalar 0.0
}
# plotData --
# PLot the result
#
# Arguments:
# time Time in the computation
# values List of values
#
# Side effects:
# Graph is updated
#
proc plotData {time values} {
.c delete data
.c delete title
$::p title "Time = [format "%5.2f" $time]"
set x [expr {0.5 * $::deltx}]
foreach v $values {
set x [expr {$x + $::deltx}]
$::p plot data $x $v
}
$::p plot data {} {} ;# Break the line of data
after 100 {
set go 1
}
vwait go
}
# main --
# Create the tensors, store a few
# computational paramters and then
# run the time loop
#
set velocity 1.0
set friction 0.0
set number 1000
set length 10.0
set deltx [expr {$length/$number}]
set deltt 0.001
tensor::create u -size [expr {$number+1}] -type double
tensor::create h -size [expr {$number+1}] -type double
#
# Initial condition
#
u = scalar 0.0
h = scalar 0.0
#
# Loop over time
#
pack [canvas .c -bg white -width 500 -height 300]
set p [::Plotchart::createXYPlot .c {0 10.0 1.0} {-2.0 2.0 0.5}]
tkwait visibility .c
set t 0
while { $t < 100000} {
set time [expr {$deltt * $t}]
if { $t % 200 == 0 } {
plotData $time [h]
}
setBoundaryConditions $time
nextTime
incr t
}Here is a snapshot:
TV Yah yah, I know I've been into some interesting materials.
AM And here is another example: Solving a 2D diffusion problem with the Tensor package