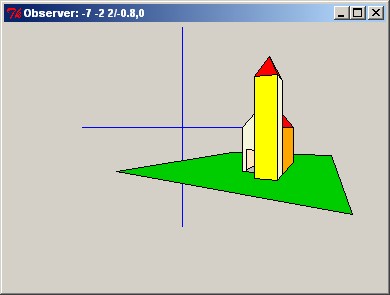
St John's chapel
Richard Suchenwirth 2002-04-07 (but brought here almost 2 years later) - In Playing 3D, first steps were taken to represent 3D objects in memory, and render them by projection on a 2D canvas. The unsatisfying part was that the positions of the "observer" were limited to curvy trajectories along the x axis, or very flat views parallel to the 3D axes. In this continuation I experiment with freely choosable observer position, so you can really "walk through" the scene, a little church on a green meadow which I call St John's chapel. Use cursor keys, possibly modified with Shift or Alt, to experiment what you can do. "+"/"-" to zoom in or out; "x", "y", "z" to see a projection along one of the main axes; "3" to return to 3D display.
There are still many shortcomings to this code, especially when you try to walk inside the church - corrections are very welcome! I suspect the 3d'project proc has bugs, but my math books couldn't help me further...
Maybe a bit more explanation is needed. The "observer" is at the position x0,y0,z0 (elements in the 3d array); his angle of looking is stored in hy0 and hz0.
proc 3d'reset {} { variable 3d array set 3d { x0 3 y0 -3 z0 3 hy0 0 hz0 0 hyi 0 hzi 0 zoom 50 flat 3d } } # Create a new polygon proc 3d'poly {id points args} { variable 3d lappend 3d(polygons) $id set 3d($id) [list $points $args] } # Map a point in 3D space to a x/y location in 2D space on the canvas proc 3d'project {point} { variable 3d; variable proj set factor $3d(zoom) if {![info exist proj($point)]} { foreach {x y z} $point break if {$z == ""} {set z 0} set rxy 0; set rxz 0 switch -- $3d(flat) { x {set x [expr {$y*$factor}]; set y [expr {-$z*$factor}] ;# side view} y {set x [expr {$x*$factor}]; set y [expr {-$z*$factor}] ;# front view} z {set x [expr {$x*$factor}]; set y [expr {-$y*$factor}] ;# top view} default { set dx [expr {$x-$3d(x0)}] set dy [expr {$y-$3d(y0)}] set dz [expr {$z-$3d(z0)}] set 3d(hy0) [expr {-atan2($3d(y0),$3d(x0))+$3d(hyi)}] set 3d(hz0) [expr {-atan2($3d(z0),$3d(y0))+$3d(hzi)}] set 3d(hy0) $3d(hyi) set 3d(hz0) $3d(hzi) set rxy [expr {hypot($dx,$dy)}] if {$rxy} { set ay [expr {-atan2($dy,$dx)+$3d(hy0)}] } else {set ay 0 ;#$3d(hy0)} set t $rxy set rxz [expr {hypot($t,$dz)}] if {$rxz} { set az [expr {+atan2($dz,$t)-$3d(hz0)}] } else {set az 0 ;#$3d(hz0)} set x [expr {cos($ay) * $3d(zoom)*2}] set y [expr {-sin($az) * $3d(zoom)*2}] } } set proj($point) [list $rxy $x $y] } #debug'locals set proj($point) } # This is called whenever a parameter has changed proc 3d'redraw {w} { variable 3d; variable proj $w delete all $w create line -100 0 100 0 -fill blue $w create line 0 -100 0 100 -fill blue catch {unset proj} set tmp {} foreach id $3d(polygons) { set sum 0 set n 0 foreach point [lindex $3d($id) 0] { set sum [expr {$sum+[lindex [3d'project $point] 0]}] incr n } puts [list $sum $n [expr {$sum/$n}] $id] lappend tmp [list [expr {$sum/$n}] $id] } set sorted {} foreach i [lsort -real -index 0 -decr $tmp] { lappend sorted [lindex $i 1] } foreach id $sorted { foreach {points args} $3d($id) break set 2dpoints {} foreach point $points { eval lappend 2dpoints [lrange [3d'project $point] 1 end] } eval $w create poly $2dpoints -outline black $args -tag $id } $w lower bg $w config -scrollregion [$w bbox all] wm title . "Observer: $3d(x0) $3d(y0) $3d(z0)/$3d(hy0),$3d(hz0)" } proc sgn x {expr {$x>0? 1: $x<0? -1: 0}} proc debug'locals {} { uplevel 1 { puts ----------[info level 0] foreach i [lsort [info locals]] { if {![array exists $i]} {puts $i=[set $i]} } } } # Building the chapel from polygons: catch {console show} ;# not available on Unix 3d'reset 3d'poly lawn {{-3 -3} {7 -3} {7 6} {-3 6}} -fill green3 -tag bg 3d'poly towerbot {{0 0 0} {0 1 0} {1 1 0} {1 0 0}} -fill blue 3d'poly towerfront {{0 0 0} {0 0 4} {1 0 4} {1 0 0}} -fill beige 3d'poly towerleft {{0 0 0} {0 1 0} {0 1 4} {0 0 4}} -fill yellow 3d'poly towerback {{0 1 0} {0 1 4} {1 1 4} {1 1 0}} -fill beige 3d'poly towerright {{1 0 0} {1 1 0} {1 1 4} {1 0 4}} -fill beige 3d'poly trfront {{0 0 4} {.5 .5 5} {1 0 4}} -fill red 3d'poly trback {{0 1 4} {.5 .5 5} {1 1 4}} -fill red 3d'poly trleft {{0 0 4} {.5 .5 5} {0 1 4}} -fill red 3d'poly trright {{1 0 4} {.5 .5 5} {1 1 4}} -fill red 3d'poly floor {{1 0} {4 0} {4 2} {1 2}} -fill grey 3d'poly front {{1 0} {4 0} {4 0 2} {1 0 2}} -fill orange 3d'poly left {{1 0} {1 0 2} {1 1 3} {1 2 2} {1 2} {1 1.8} {1 1.8 1} {1 1.3 1} {1 1.3}} -fill beige ;# with door 3d'poly back {{1 2} {4 2} {4 2 2} {1 2 2}} -fill bisque 3d'poly right {{4 0} {4 0 2} {4 1 3} {4 2 2} {4 2}} -fill bisque 3d'poly rfront {{1 0 2} {4 0 2} {4 1 3} {1 1 3}} -fill red 3d'poly rback {{1 2 2} {4 2 2} {4 1 3} {1 1 3}} -fill red pack [canvas .c] -fill both -expand 1 3d'redraw .c # Key bindings: bind . <Escape> {exec wish $argv0 &; exit} bind . <Up> {set 3d(z0) [expr $3d(z0)+1]; 3d'redraw .c} bind . <Down> {set 3d(z0) [expr $3d(z0)-1]; 3d'redraw .c} bind . <Left> {set 3d(x0) [expr $3d(x0)-1]; 3d'redraw .c} bind . <Right> {set 3d(x0) [expr $3d(x0)+1]; 3d'redraw .c} bind . <Alt-Up> {set 3d(y0) [expr $3d(y0)+1]; 3d'redraw .c} bind . <Alt-Down> {set 3d(y0) [expr $3d(y0)-1]; 3d'redraw .c} bind . <Shift-Up> {set 3d(hzi) [expr $3d(hzi)-.1]; 3d'redraw .c} bind . <Shift-Down> {set 3d(hzi) [expr $3d(hzi)+.1]; 3d'redraw .c} bind . <Shift-Left> {set 3d(hyi) [expr $3d(hyi)-.1]; 3d'redraw .c} bind . <Shift-Right> {set 3d(hyi) [expr $3d(hyi)+.1]; 3d'redraw .c} bind . x {set 3d(flat) x; 3d'redraw .c} bind . y {set 3d(flat) y; 3d'redraw .c} bind . z {set 3d(flat) z; 3d'redraw .c} bind . 3 {set 3d(flat) 3; 3d'redraw .c} bind . + {set 3d(zoom) [expr $3d(zoom)*2]; 3d'redraw .c} bind . - {set 3d(zoom) [expr $3d(zoom)*0.5]; 3d'redraw .c} bind . r {3d'reset; 3d'redraw .c} update; raise .
Richard, you're an absolutely brilliant programmer. What you can do in 100 lines of Tcl is just amazing. But as regards 3D, you'd be a zillion times more effective in Quake.
The Quake game engine and derivatives of it is what 99% of today's computer games are written in. And the 3D Worlds that these game engines support are fantastically accurate and realistic. They not only support 3D buildings that you can walk around in, but wallpaper, and water, and rain, and grass and flowers, and people you can interact with too.
And better still, Quake (the early but still very powerful versions of it,) are OPEN SOURCE. And even better is the way the Quake developers have implemented the entire system. In brief there's:-
- Typically GUI based editers like Worldcraft, for creating the 3D Worlds...
- MAP files - which are plain ASCII text files - which store the 3D World definitions in...
- Compiler tools, which convert the MAP files into the BSP (binary) files that the game engine EXEs actually run.
- And of course, the game engines themselves.
Now the Quake game engines are absolutely brilliant at running/rendering the 3D Worlds. The problem with 3D Worlds is not the rendering of them - but CREATING them. Even with tools like Worldcraft, it is still a painfully tedious process.
But the MAP files that describe those worlds are ASCII TEXT files! Which of course, are easily created from Tcl/Tk. As are the GUI based tools to create/edit the descriptions of the 3D worlds in. So if you were to get onto the Net - and download the Quake compiler tools and game engine - I'm sure you'd be more effective. Forget about rendering St John's Chapel - Quake can do that. It's (efficiently) creating the 3D description that's the problem. Regards, Peter Newman.
RS: Thanks for the hint! But as so often, I was less interested in doing 3D rendering as such, but to explore what all can be done in pure-Tcl (and understand basic algorithms by that, too.) Also, a decent MAP file editor would of course have to render what you have so far (plus interactive help etc.), so rendering 3D polygons on a canvas is an issue in any case.
Peter Newman: I understand. But as regards "basic algorithms", and "what can be done in pure Tcl", we can still learn much from Quake. The Quake guys are the only people who've come up with a system for modelling and rendering a 3D world that works (and works on standard home computers - rather than special supercomputers or the like). So if you want to know about 3D, Quake is 3D 101 to 3D 501 inclusive.
As regards "what can be done from pure Tcl", Quake tells us the answer there too. What can be done from pure Tcl is what you're already doing. In other words, you can never hope to render/explore 3D worlds effectively from pure Tcl - all you can do is create the simplistic 3D models that guide the 3D world designer as they're creating them.
There are (at least) two reasons for this:-
LIGHTING St Johns Chapel as you have it now comprises rectangular surfaces in a single colour in 3D space. To make it more realistic, you could paint textures (hand-drawn or photographs) on it. It'll look much better - but it will still look fake. To make it look real, you must take lighting into account. Any evenly-lit 3D world looks fake. If you look around at the light streaming in the window, and the resultant shadows and light and dark patches all over the room, you'll realise why. The human brain simply won't accept an evenly lit 3D world as being real. After a few years work, the Quake developers realised this - and split the Quake compiler into two parts - one to compile the 3D world for rendering, and the other to light it. In other words, rendering is only half the story. You've also got to light the 3D world.
BSP FILES: If you look at St Johns Chapel in the screenshot above, you'll note the viewer is looking at the front and right sides of the church. The back and left sides and the interior of the church are obscured, and needn't be drawn. In any given 3D world there will be hundreds if not millions of rectangular surfaces to be drawn, painted and lit. And trying to draw them all will bring even the most powerful computer to it's knees. The solution, in Quake's case, is the "Binary Space Partition" tree. That's what the BSP in BSP files stands for. It's a data structure that allows the run-time engine to rapidly identify the surfaces that need to be drawn, for any given viewer position. For a given 3D world, it can take literally hours to create this data structure (from the info. stored in the MAP file), and store it in the BSP file, so that the viewer can move around the 3D world in real-time at reasonable speed.
Taking the above two points into account, you'll see that "what can be done from pure Tcl" is what you're already doing. You can't write the tools for the user to explore the finished 3D world in pure Tcl. All you can do is write the tools for the 3D world developer to explore a simplistic variant of that 3D world as they're creating it.
I just mention this because what you're doing is valuable work. If you combine your software for drawing 3D worlds on the canvas with:-
- A data file format (perhaps in XML), for storing the 3D world definitions in,
- A conversion tool for converting that data file to a MAP file, and;
- Some GUI based program for editing the data file - whilst seeing your software draw the work in progress as you go,
then you've got a seriously useful piece of software. But obviously, all those tools have integrate and work together.
A 3D version of your TclBrix for example - together with the above enhancements - would be most useful.}
Completely off-topic, but I noticed this page because there is a town in Durham (NE England) of that name:-
RS:-) I don't know that place, I was just instigated by a chapel model in a math book, and I named it after who might be the patron saint of Tcl/Tk...
LV: I am relatively certain that our St. John would really get a chuckle out of this.